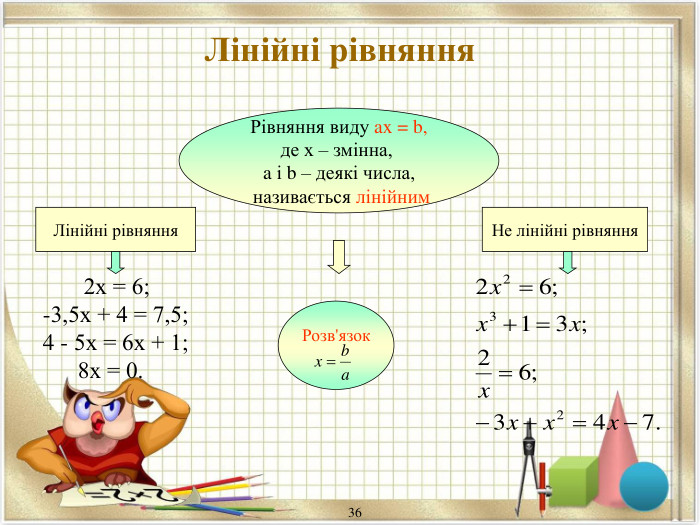
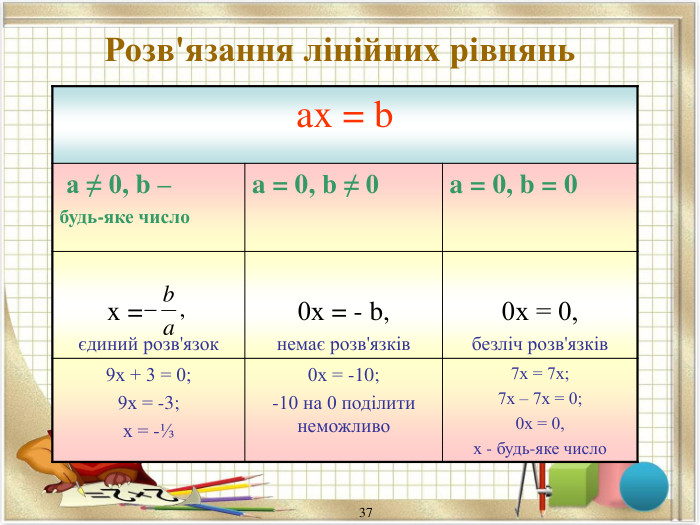
Опорні схеми. Лінійні рівняння та їх системи
Про матеріал
Опорні конспекти та схеми, зміст і послідовність яких відповідають чинній програмі з алгебри для 7 класу НУШ
Дані конспекти можуть використовуватись вчителями та учнями для вивчення нового матеріалу, на уроках формування вмінь і навичок, для узагальнення і систематизації знань та вмінь, для виготовлення таблиць та презентацій.
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку