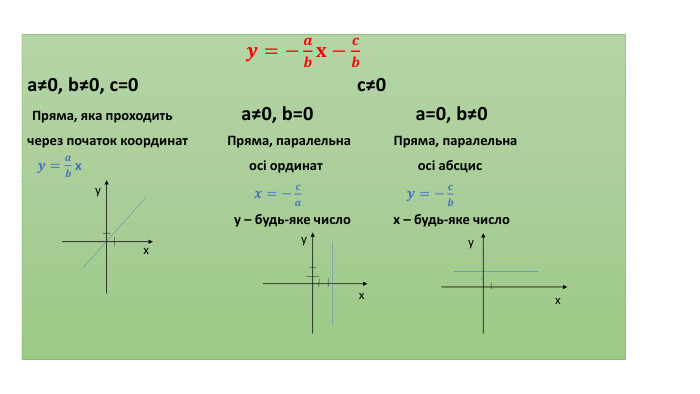
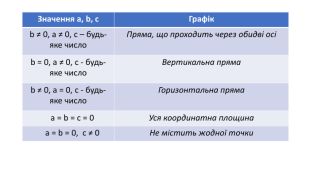
Лінійні рівняння з двома змінними та його графік
Про матеріал
Презентація "Лінійне рівняння з двома змінними та його графік", містить теоретичну та практичну частини. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку