Мала академія наук України «Пряма і обернена теорема Вієта та їх застосування»

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ

ВИКОНАВЧОГО ОРГАНУ КИЇВСЬКОЇ МІСЬКОЇ РАДИ

(КИЇВСЬКОЇ МІСЬКОЇ ДЕРЖАВНОЇ АДМІНІСТРАЦІЇ)

КИЇВСЬКЕ ТЕРИТОРІАЛЬНЕ ВІДДІЛЕННЯ

МАЛОЇ АКАДЕМІЇ НАУК УКРАЇНИ

(КИЇВСЬКА МАЛА АКАДЕМІЯ НАУК)

 

Відділення: математика

Секція: алгебра та початки аналізу

Базова дисципліна: математика

 

 

 

 

Пряма і обернена теорема Вієта та їх застосування

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

 

1.	Вступ
2.	Теорема Вієта та її застосування ………………………………………………		5
	2.1	Життєвий та творчий шлях Франсуа Вієта ……………………………..	5
	2.2	Заслуги Франсуа Вієта в математиці ……………………………………	7
	2.3	Цікаві факти з життя та діяльності вченого …………………………….	8
	2.4	Квадратні рівняння ……………………………………………………….	8
	2.5.	Теорема Вієта та її застосування ………………………………………..	11
	2.6	Обернена теорема Вієта ………………………………………………….	13
3.	Висновки ………………………………………………………………………..		15
	Перелік використаних джерел ……………………………………………........		16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

По праву в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого:

Умножишь ты корни и дробь уж готова:

В числителе с, в знаменателе а,

А сумма корней тоже дроби равна

Хоть с минусом дробь эта, что за беда-

В числителе b, в знаменателе a.

І. Дирченко

Про математику, її історію, особливості, неповторну красу можна говорити нескінченно. Любов до цієї науки стає ще більше, коли побачиш не тільки саму науку, а й тих, хто цілком присвятив себе великій справі і висвітлював в ній шлях далеко вперед.

Творці науки – це люди, що відрізняються винятковою цілеспрямованістю, відданою працею, відповідальністю перед людством за результати своїх досліджень. Творці математики – це люди з дивовижними долями, з сильними характерами, котрі долають труднощі і негаразди.

У 2017 році виповнилося 477 років з дня народження чудового французького математика, який поклав початок алгебрі як науці про перетворення виразів, творця літерного обчислення, Франсуа Вієта.

Математична освіта, що отримується в загальноосвітній школі, є найважливішим компонентом загальної освіти і загальної культури сучасної людини. Практично все, що оточує сучасну людину – це все так чи інакше пов'язане з математикою. А останні досягнення у фізиці, техніці та інформаційних технологіях не залишають жодного сумніву, що і в майбутньому стан речей залишиться незмінним. Тому вирішення багатьох практичних завдань зводиться до розв’язування різних видів рівнянь, які необхідно навчитися вирішувати.

Ми досить часто стикаємося з рівняннями, розв’язок яких вимагає довгих обчислень, а іноді і ці обчислення не приносять успіху. І як наслідок, виникає питання: а чи не можна для цього рівняння знайти простий, раціональний, короткий розв’язок. Необхідно пам'ятати, що кожна математична задача вимагає індивідуального підходу. Не завжди корисно слідувати загальним алгоритмам, відхилення від них, іноді призводить до більш раціонального вирішення.

  При розв’язуванні квадратних рівнянь, теорема Вієта відіграє величезну роль. Отримані Вієтом системи рівностей, що зв'язують корені рівняння довільного степеня з їх коефіцієнтами, тепер називаються теоремою Вієта, і кожен учень сьогодні знає це ім'я.

Дослідження Вієта дали абсолютно новий напрямок роботи своїх сучасників, а алгебраїчні ідеї його внесли великий вклад в європейську науку, він прославився узагальненням алгебри.

Методи вивчення: опрацювання джерел інформації про вклад вченого в розвиток математики, пряму та обернену теорему Вієта.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2

ТЕОРЕМА ВІЄТА ТА ЇЇ ЗАСТОСУВАННЯ

2.1  Життєвий та творчий шлях Франсуа Вієта

Франсуа Вієт – французький математик, що запровадив сучасну систему нотації в алгебрі.

Народився 1540 року на півдні Франції у невеликому містечку Фонтене-ле-Конт провінції Пуату, що розташоване за 60 км від Ла-Рошель, що була на той час оплотом французьких протестантів-гугенотів (послідовників кальвінізму). Більшу частину життя він прожив поряд із керівниками цього руху, хоча сам залишався католиком. Релігійні незгоди вченого не турбували.

Батько Франсуа був прокурором. За традицією, син обрав професію батька й став юристом, закінчивши університет у Пуату. 1560 року двадцятирічний адвокат почав свою кар'єру в рідному місті. Як адвокат Вієт користувався у населення авторитетом та повагою. Але через три роки перейшов на службу до відомої гугенотської сім'ї де Партене. Він став секретарем власника будинку й учителем його дочки, дванадцятирічної Катерини. Саме її навчання викликало в молодого юриста зацікавленість до математики.

Коли учениця виросла та вийшла заміж, Вієт не розлучився з її родиною й перебрався з нею до Парижу, де йому було легше дізнатися про досягнення провідних математиків Європи. З деякими вченими Вієт познайомився особисто. Він спілкувався з відомим професором Сорбонни Рамусом, вів дружнє листування з відомим математиком Італії Рафаелем Бомпеллі.

Близько 1570 року підготував «Математичний Канон» - капітальна праця з тригонометрії, який видав в Парижі в 1579 році. 1571 року Вієт перейшов на державну службу й став радником парламенту в Бретані. Знайомство з Генріхом Наварським, майбутнім королем Франції Генріхом IV, допомогло Вієту отримати почесну придворну посаду – таємного радника – спочатку короля Генріху ІІІ, а потім – і Генріха IV.

Франсуа Вієт здобув славу під час франко-іспанської війни, коли йому вдалось розкрити шифр, який король Філіп ІІ використовував для кодування дипломатичних листів. Це був підстановочний шифр, що складався з 500 символів, якими замінювались літери алфавіту, склади, а також широковживані імена та поняття. У 1589 році Вієту вдалось розшифрувати лист іспанського короля до Хуана Морео, командувача військами у Франції. Пізніше іспанцям стало відомо, що шифр для французів уже не таємниця, і що його розшифрував Вієт. Впевнені в неможливості розгадати спосіб тайнопису людьми, вони звинуватили Францію перед папою римським та інквізицією в підступах диявола. Шифр було змінено, однак Вієт і надалі міг його розуміти. Наприклад, у 1601 році він розкрив зміст листів іспанського посла у Римі.

Перебуваючи на державній службі, Вієт залишався вченим. До того часу належать свідоцтва сучасників Вієта про його величезну працездатність.

1584 року через наполягання Гізів Вієта звільнили з посади та послали до Парижу. Саме на цей період припадає розквіт його діяльності. Отримавши несподіваний спокій та відпочинок, вчений поставив собі мету скласти всеосяжну математику, яка дозволила б розв'язувати будь-які задачі. У нього склалося переконання, «що має існувати загальна, невідома ще наука, яка охоплює й розумні роздуми найновіших алгебраїстів, і глибокі геометричні досліди давніх».

У 1593 голландський математик Андріан ван Ромен запропонував позмагатись з ним, вирішивши задачу: розв’язати рівняння 45-го степеня. Завдання було надіслане відомим ученим того часу, однак серед них не було жодного француза. Посол Нідерландів у Парижі звернув увагу короля Генріха IV, сказавши, що, мабуть, у Франції просто немає математиків. Щоб довести протилежне, король викликав Вієта і той прямо в приймальні, у присутності короля, міністрів та гостей, знайшов один корінь запропонованого рівняння.

Пізніше Вієт знайшов ще 22 корені рівняння і описав весь процес вирішення задачі у статті «Responsum ad problema quod omnibus mathematicis totius orbis construendum proposuit Adrianus Romanus». У даного рівняння було ще 22 від’ємних корені, однак про них у праці математика не було сказано.

1589 року, після вбивства Генріха Гіза за наказом короля, Вієт повернувся до Парижу. Подробиці життя Вієта у той час невідомі. Відомо лише, що він перейшов на службу до Генріха IV, перебував при дворі, був відповідальним урядовцем і користувався великою повагою як математик.

В останні роки життя Вієт пішов з державної служби, але продовжував цікавитися наукою. Відомо, що він вступив у полеміку з приводу запровадження нового григоріанського календаря і навіть хотів створити власний календар. 14 лютого 1603 р. Вієт, людина великого розуму і розсудливості, один з найбільш вчених математиків століття, помер у Парижі. Йому було більше шістдесяти років».

2.2 Заслуги Франсуа Вієта в математиці

Франсуа Вієт сам не вважав себе математиком. Він говорив, що займається математикою у вільний час для власного задоволення. При цьому, маючи великі статки, свою працю він за свій рахунок видавав і розсилав ученим в усі куточки Європи.

Франсуа Вієт – математик, який поклав початок алгебрі як науці про перетворення виразів, про рішення рівнянь в загальному вигляді, творець літерного числення. У працях Вієта алгебра стає загальною наукою про алгебраїчні рівняння, заснованої на символічних позначеннях. Вієт перший позначив буквами не тільки невідомі, але й дані величини, тобто коефіцієнти відповідних рівнянь. Завдяки цьому стало вперше можливим вираження властивостей рівнянь і їх коренів загальними формулами, і самі алгебраїчні вирази перетворилися в об'єкти, над якими можна проводити дії. Вієт розробив однаковий прийом розв’язку рівнянь 2-ого, 3-ого і 4-го степеня і новий метод розв'язання кубічного рівняння, дав тригонометричний розв’язок рівняння 3-го степеня, запропонував різні раціональні перетворення коренів, встановив залежність між коренями та коефіцієнтами рівнянь (формули Вієта).

Вієт показав, що, оперуючись символами, можна отримати результат, який можна застосувати до будь-яких відповідних величин, тобто вирішити задачу в загальному вигляді. Це поклало початок корінного перелому в розвитку алгебри: стало можливим буквене числення.

Головні відкриття Ф. Вієта викладені в знаменитому «Запровадження в аналітичне мистецтво», опублікованому в 1591 році.

2.3 Цікаві факти з життя та діяльності вченого

2.4 Квадратні рівняння

Рівняння самі по собі становлять інтерес для вивчення, тому що саме з їх допомогою на символічній мові записуються найважливіші завдання пізнання реальної дійсності. Алгебра як мистецтво розв'язувати рівняння зародилася дуже давно в зв'язку з потребами вирішувати завдання, пов'язані з перебуванням площ земельних ділянок, з земляними роботами військового характеру, а також з розвитком астрономії і самої математики. Найбільш ранні рукописи свідчать про те, що в Стародавньому Вавилоні і Давньому Єгипті, були відомі способи розв’язку лінійних рівнянь. Квадратні рівняння вміли вирішувати близько 2000 років тому до н.е. вавилоняни. У «Арифметиці» Діофанта міститься ряд завдань, що вирішуються за допомогою складання рівнянь різних степенів.

Неповні квадратні рівняння і часткові випадки повних квадратних рівнянь вміли вирішувати вавилоняни (приблизно за 2 тисячі років до нової ери). Деякі види квадратних рівнянь вирішували давньогрецькі математики, зводячи їх розв’язок до геометричних побудов. Правило розв’язку квадратних рівнянь, приведених до виду ах² + bх + с = 0, де а > 0, дав індійський вчений Брахмагупта (VII ст.). Виведення формули коренів квадратного рівняння в загальному вигляді є у Вієта, проте він визнавав лише додатні корені. Італійські математики XVI в. враховували крім додатних і від’ємні корені. Лише в XVII ст. завдяки працям Жирара, Декарта, Ньютона та інших вчених, спосіб вирішення квадратних рівнянь приймає сучасний вигляд.

Квадратним рівнянням називається рівняння вигляду

ax² + bx + c = 0 (a0),    (2.4.1)

де х – змінна, a, b, c – деякі числа, причому

Числа a, b, c називають коефіцієнтами квадратного рівняння: а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член.

Якщо , рівняння називається зведеним квадратним рівнянням.

Наприклад: x² – 6x + 1 = 0.

Якщо , рівняння називається не зведеним квадратним рівнянням.

Наприклад: 3x² – 8x + 15 = 0.

Якщо у квадратному рівнянні хоча б один із коефіцієнтів b або с дорівнює 0, то таке рівняння називається неповним квадратним рівнянням.

Наприклад:  x² + 15 = 0.

Способи розв’язування неповних квадратних рівнянь:

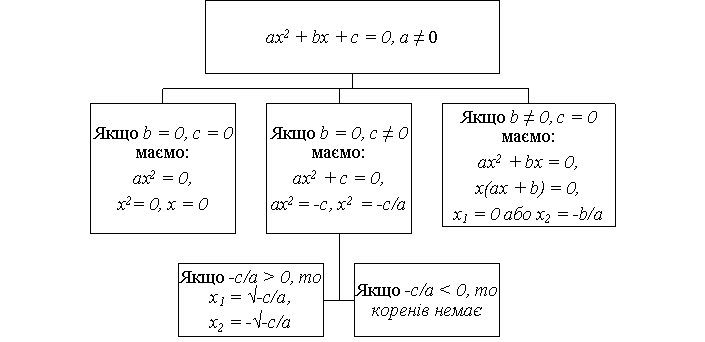
Розглянемо повне квадратне рівняння ax² + bx + c = 0 (a0). Корені даного рівняння знаходять за формулою

     (2.4.2)

Вираз b² – 4ac називається дискримінантом (від латинського розрізняючий) і позначається літерою D.

1. Якщо D < 0, рівняння не має дійсних коренів.     

2. Якщо D = 0,  рівняння має один корінь:          (2.4.3)

3. Якщо D > 0, рівняння має два корені:          (2.44)

Для квадратних рівнянь із парним другим коефіцієнтом зручніше користуватися формулою:

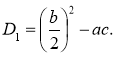     (2.4.5)

Тоді для , маємо

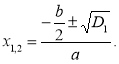      (2.4.6)

Наприклад:

1. Знайти корені квадратного рівняння

• x² – 26x + 120 = 0

D = 26² - 4·120·1 = 676 – 480 = 196 > 0 – рівняння має два корені

,

• 9x² – 12x + 4 = 0.

D = (-12)² - 4·9·4 = 144 – 144 = 0 – рівняння має один корінь

• x² + x + 6 = 0.

D = 1² - 4·6·1 = 1 – 24 = – 23 – рівняння не має дійсних коренів

• x² – 10x – 24 = 0.

D₁ = (-10/2)² - 1·(-24) = 25 + 24 = 49 > 0 – рівняння має два корені

,

2. Знайти довжину сторін прямокутника, якщо його периметр 18 см, а площа 77 см².

Розв’язування:

    Позначимо х – більшу сторону, тоді 18 – x менша його сторона. Площа прямокутника дорівнює добутку цих довжин:

х · (18 – х)= 77     або     х² – 18х + 77 = 0.

D = 18² – 4·77·1 = 16 > 0 – рівняння має два корені

,

Якщо х = 11, то 18 – х =7,

Відповідь: 7 см, 11 см.

2.5 Теорема Вієта

Теорема Вієта – формули, що виражають коефіцієнти многочлена через його корені. Ці формули зручно використовувати для перевірки правильності знаходження коренів та для задання многочлена з визначеними властивостями.

 

 

Теорема Вієта:

Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів дорівнює вільному члену.

Доведення теореми:

Нехай х₁ та х₂ – корені зведеного квадратного рівняння x² + px + q = 0, дискримінант якого D = p² – 4q.

Якщо D > 0, то рівняння має два корені:

 та     (2.5.1)

Якщо D = 0, то рівняння має два однакових корені:

      (2.5.2)

Знайдемо суму та добуток коренів:

  (2.5.3)

  (2.5.4)

Отже, ; . Теорему доведено.

Використовуючи теорему Вієта, можна записати відповідні формули і для коренів будь-якого незведеного квадратного рівняння ax² + bx + c = 0 (a0).

Оскільки a0, поділимо обидві частини рівняння на а. Одержимо зведене квадратне рівняння:

     (2.5.5)

Тоді за теоремою Вієта:

;     (2.5.6)

Наприклад:

1. Не розв’язуючи рівняння 3x² – 5x – 7 = 0, знайдіть суму та добуток його коренів.

Розв’язування:

Знайдемо дискримінант рівняння, щоб пересвідчитись, що корені існують:              D = 5² – 4·3·(-7) > 0 – рівняння має два корені х₁ та х₂.

Отже, за теоремою Вієта:

; 

Відповідь: та .

2. Один із коренів рівняння x² + рx – 18 = 0 дорівнює 3. Знайдіть коефіцієнт р та другий корінь рівняння.

Розв’язування: Нехай х₁ = 3 – один із коренів рівняння, а х₂ – другий його корінь. За теоремою Вієта: ;  . Ураховуючи, що    х₁ = 3, маємо:

     

Відповідь: , .

2.6 Теорема, обернена до теореми Вієта:

Якщо деякі два числа m і n такі, що їхня сума дорівнює другому коефіцієнту зведеного квадратного рівняння, узятому з протилежним знаком, а їхній добуток дорівнює його вільному члену, то дані числа є коренями цього зведеного квадратного рівняння x² + px + q = 0.

Доведення оберненої теореми:

За умовою ; . Тому рівняння x² + px + q = 0 можна записати наступним чином:

x² – (m + n)x + mn = 0.

Перевіримо, чи є число m коренем цього рівняння, для цього підставимо в ліву частину рівняння замість змінної х число m. Одержимо:

m ² – (m + n)m + mn = m ² – m² – nm + mn = 0.

Отже, m – корінь цього рівняння.

Аналогічно, підставимо в ліву частину рівняння замість змінної х число n. Одержимо:

n ² – (m + n)n + mn = n ² – n ² – nm + mn = 0,

тобто n – також корінь цього рівняння.

Отже, m і n – корені рівняння x² + px + q = 0, що й треба було довести.

Під час розв'язування треба також враховувати такі висновки з теореми Вієта:

1.  Якщо q < 0, х₁ і х₂ мають різні знаки.
2.  Якщо q > 0, х₁ і х₂ обидва від'ємні чи обидва додатні. Знак  суми х₁ і х₂ є протилежним до знака р.  

Наприклад:

1. Складіть зведене квадратне рівняння, коренями якого є числа -5 та 2.

Розв’язування: Шукане квадратне рівняння має вигляд x² + px + q = 0. За теоремою, оберненої до теореми Вієта:

p = – (х₁ + х₂) = – (–5 + 2) = 3

q = х₁ · х₂ = –5 · 2 = –10.

Отже,  x² + 3x – 10 = 0 – шукане рівняння.

Відповідь: x² + 3x – 10 = 0

2. Розв’яжіть рівняння: х² – 8х – 9 = 0.

За теоремою Вієта: х₁ х₂ = – 9;  х₁ +  х₂ = 8;  9 = 1 ^. 9 = 3 ^. 3. Очевидно, що                  8 = 9 + (-1).

Відповідь: х₁ = -1; х₂ = 9.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

Працюючи над темою «Пряма та обернена теорема Вієта», я переконався, що вона надзвичайно важлива і актуальна з усіх розділів математики.

У 16 столітті європейські математики зуміли, нарешті, зрівнятися в мудрості з древніми греками і перевершити їх там, де успіхи були не великі. Зокрема, Франсуа Вієт показав, що, оперуючи символами, можна отримати результат, який можна застосувати до будь-яких величин, тобто вирішити задачу в загальному вигляді.

Теорема Франсуа Вієта стала найзнаменитішим твердженням шкільної алгебри. Теорема Вієта гідна захоплення, тим більше що її можна узагальнити на многочлени будь-якого степеня. При розв’язуванні рівнянь з використанням теореми Вієта швидкість розв’язку зростає в кілька разів.

Запропонована робота дозволяє повторити всі основні прийоми розв’язування квадратних рівнянь, пов'язані із застосуванням теореми Вієта і оберненої теореми.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Істер О.С. Алгебра: підруч. для 8-го кл. загальноосвіт. Навч. Закл. / О.С. Істер. – Київ: Генеза, 2016. – 272 с.
2. Мерзляк А.Г., Полонський В.Б., Рябінович Ю.М., Якір М.С. Збірник задач і контрольних робіт з алгебри для 8 класу. – Х.: Гімназія, 2016. – 96 с.: іл.
3. Кучевський М. І., Квадратні рівняння. //Математика в школах України. – 2007. –  С. 34-38.
4. Математична енциклопедія / т.2, під ред. Виноградова  І.М.  М.: Радянська енциклопедія, 1979 р.
5. Перельман,  Я.І. Цікава алгебра. / Я. І. Перельман – М.: Наука, 1976 р.
6. ru.wikipedia.org/wiki …