Самостійна робота. Квадратичні нерівності

Про матеріал

Самостійна робота. Квадратичні нерівності Запропонований матеріал допоможе вчителеві швидко перевірити знання з даної теми. Завдання ідуть по наростанню, тому кожному учневі доступно оцінити свій рівень знань з даної теми.

Перегляд файлу

Клас	Прізвище, ім’я	Варіант	Дата	Оцінка
9–__	________________________________ __________________________	_____	___.___.20__

Самостійна робота. Квадратичні нерівності

1. (2 бали) На малюнку зображено графік функції . Вказати розв’язок нерівності

Варіант 1 x2 – 6х + 8 < 0. Варіант 2 x2 – 6х + 8 ≥ 0.

А	Б	В	Г
(– ∞;2][4;∞)	(– ∞;2)(4;∞)	[2;4]	(2;4)

2. (3 бали) Розв’язати нерівність: Варіант 1 (х + 3)(x – 1) > 0. Варіант 2 (х – 3)(x + 1) < 0.

А	Б	В	Г
(– ∞;– 3)(1;∞)	(– 3;1)	(–1;3)	(– ∞;– 1)(3;∞)

Клас	Прізвище, ім’я	Варіант	Дата	Оцінка
9–__	________________________________ __________________________	_____	___.___.20__

Самостійна робота. Квадратичні нерівності

1. (2 бали) На малюнку зображено графік функції . Вказати розв’язок нерівності

Варіант 1 x2 – 6х + 8 < 0. Варіант 2 x2 – 6х + 8 ≥ 0.

А	Б	В	Г
(– ∞;2][4;∞)	(– ∞;2)(4;∞)	[2;4]	(2;4)

2. (3 бали) Розв’язати нерівність: Варіант 1 (х + 3)(x – 1) > 0. Варіант 2 (х – 3)(x + 1) < 0.

А	Б	В	Г
(– ∞;– 3)(1;∞)	(– 3;1)	(–1;3)	(– ∞;– 1)(3;∞)

3. (3 бали) Розв’язати нерівність: Варіант 1 x2 – 2х – 24 ≤ 0. Варіант 2 x2 + 2х – 24 ≥ 0.

А	Б	В	Г
(– ∞;– 4][6;∞)	[– 4;6]	[– 6;4]	(– ∞;– 6][4;∞)

4. (4 бали) Розв’язати систему нерівностей: Варіант 1 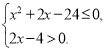Варіант 2

Відповідь: __________________________

3. (3 бали) Розв’язати нерівність: Варіант 1 x2 – 2х – 24 ≤ 0. Варіант 2 x2 + 2х – 24 ≥ 0.

А	Б	В	Г
(– ∞;– 4][6;∞)	[– 4;6]	[– 6;4]	(– ∞;– 6][4;∞)

4. (4 бали) Розв’язати систему нерівностей: Варіант 1 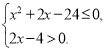Варіант 2

Відповідь: __________________________

doc

Завантажити

Зберегти на потім

Додав(-ла)

Здоренко Тетяна Петрівна

Пов’язані теми

Алгебра, 9 клас, Матеріали до уроків

Додано

16 липня 2020

Переглядів

751

Оцінка розробки

Відгуки відсутні