Матеріал до позакласного заходу з математики "Краса простих чисел"

Про матеріал

Матеріал для позакласного заходу з математики та інформатики та "Краса простих чисел" для 6-их класів можна використовувати на математичних гуртках, на додаткових заняттях з математики та інформатики та інших позакласних заходах.

Перегляд файлу

Краса простих чисел в математиці та інформатиці

Те, що існують числа, які не діляться ні на яке інше число, люди знали ще в давнину. Послідовність простих чисел має наступний вигляд:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 ...

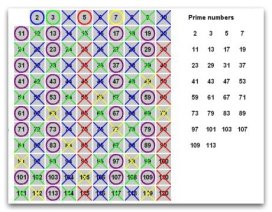$C:\Documents and Settings\Admin\Рабочий стол\resheto-eratosfena-c-algoritm-poiska-2.jpg$ Доказ того, що цих чисел нескінченно багато, дав ще Евклід, що жив в 300р. до н.е. Приблизно в ті ж роки інший грецький математик Ератосфен, придумав досить-таки простий алгоритм отримання простих чисел, суть якого була в послідовному викреслюванні чисел із таблиці. Ті, що залишилися числа, які ні на що не ділилися, і були простими. Алгоритм називається «решето Ератосфена» і за рахунок своєї простоти (у ньому немає операцій множення або ділення, тільки додавання) використовується в комп'ютерній техніці досі.

Давньогрецький вчений і письменник Ератосфен один із надзвичайно різнобічних вчених античності. Ератосфен займався філологією, філософією, хронологією, математикою, астрономією, географією, сам писав вірші і музику. За це сучасники дали йому прізвисько Пентатл, тобто Багатоборець. Інше його прізвисько, Бета, тобто "другий", очевидно, свідчило про те, що у всіх науках Ератосфен досягає не найвищого, але чудового результату.

У 245 році до н.е. цар Птолемей III Евергет запросив Ератосфена в Афіни для роботи в Олександрійській бібліотеці, де вже працювали його вчитель Калімах і Аполлоній Родоський. Ератосфен відгукнувся на запрошення, у віці близько тридцяти років він приїхав до Олександрії, де і залишився до самої смерті. Через п’ять років після приїзду він змінив Аполлонія Родоського на посаді голови Олександрійської бібліотеки. Як голова бібліотеки, Ератосфен займався навчанням дітей монарха – майбутнього правителя Птолемея IV і його сестри (а згодом і дружини) Арсіної. Він помер у 194 році до н.е., втративши посаду голови бібліотеки, до того ж він осліп. Ератосфена спіткала голодна смерть, але, ймовірно, не від безгрошів’я, а як досить жорстокий спосіб самогубства. У праці «Хронограф» він намагався встановити дати, пов’язані з історією Еллади, склав список переможців Олімпійських ігор.

Мабуть, уже під час Ератосфена стало ясно, що якого-небудь чіткого критерію, чи є число простим, не існує - це можна перевірити лише експериментально. Існують різні способи для спрощення процесу (наприклад, очевидно, що число не повинно бути парним), але простий алгоритм перевірки не знайдений до цих пір, і скоріше всього знайдено не буде: щоб дізнатися, чи просте число, треба спробувати розділити його на менші числа.

Чи актуальні прості числа сьогодні? Ще як! Прості числа є основою сучасної криптографії (наука про математичні методи забезпечення конфіденційності, цілісності і автентичності інформації), так що більшість людей користуються ними кожен день, навіть не замислюючись про це. Будь-який процес аутентифікації, наприклад, реєстрація телефону в мережі, банківські платежі тощо, вимагають криптографічних алгоритмів.

$C:\Documents and Settings\Admin\Рабочий стол\y-cegh5nd281.jpg$ Суть ідеї тут вкрай проста і лежить в основі алгоритму RSA, запропонованого ще в 1975 році. Відправник і одержувач спільно, вибирають так званий «закритий ключ», який зберігається в надійному місці. Цей ключ являє собою просте число. Друга частина - «відкритий ключ», теж просте число, формується і передається відправником у вигляді добутку разом з повідомленням відкритим текстом, його можна опублікувати навіть в газеті. Суть алгоритму в тому, що не знаючи «закритої частини», отримати вихідний текст не можливо.

В чому тут хитрість? А в тому, що добуток двох простих чисел обчислити нескладно, а ось зворотної операції не існує - якщо не знати першої частини, то така процедура може бути виконана лише перебором. І якщо взяти дійсно великі прості числа (наприклад, в 2000 символів довжиною), то декодування їх займе кілька років навіть на сучасному комп'ютері (до того часу повідомлення стане давно неактуальне).

Геніальність цієї схеми в тому, що в самому алгоритмі немає нічого секретного - він відкритий і всі дані лежать на поверхні (і алгоритм, таблиці великих простих чисел відомі). Сам шифр разом з відкритим ключем можна передавати як завгодно, в будь-якому відкритому вигляді. Але не знаючи секретної частини ключа, яку вибрав відправник, зашифрований текст ми не отримаємо. Для прикладу можна сказати, що опис алгоритму RSA було надруковано в журналі в 1977 році, там же був наведений приклад шифру. Лише в 1993 році за допомогою розподілених обчислень на комп'ютерах 600 добровольців, було отримано правильну відповідь.

Так що прості числа виявилися зовсім не настільки прості, і їх історія на цьому явно не закінчується.

Відкрито нове найбільше просте число

Міжнародна колаборація GIMPS заявила про відкриття нового найбільшого відомого простого числа, що в десятковому запису на мільйон розрядів перевершує попереднє.

26 грудня 2017 року учасники GIMPS (Great Internet Mersenne Prime Search), проекту добровільних обчислень з пошуку простих чисел Мерсенна, підтвердили відкриття нового найбільшого простого числа. Привести його тут неможливо, у десятковому запису воно складається з 23 249 425 знаків, в книзі з записом цього числа було б близько семи тисяч сторінок.

Число, яке отримало позначення M77232917, являє собою ступінь двійки мінус 1; показник ступеня дорівнює 77 232 917. Попереднє найбільше відоме просте число, відкрите у січні 2016 року, було на мільйон знаків коротше.

$C:\Documents and Settings\Admin\Рабочий стол\VIRUS21.jpg$