Матеріали до уроку "Перпендикуляр і похила"

Тема. Перпендикуляр і похила, їх властивості

Мета:ознайомити дітей з поняттям перпендикуляра і похилої, навчити  виконувати побудову перпендикуляра і похилої, розв’язувати задачі на застосування даних відрізків, задачі практичного характеру; сприяти формування математичних компетентностей, виховувати любов до предмета, повагу до думки однокласника під час роботи в парах;  розвивати пам’ять, увагу, уяву, сприяти фізично розвитку, збагачувати словниковий запас учнів, уміння і навики роботи в парах, колективної роботи, критичне мислення.

Обладнання: презентація показу, картки для гри в «Лото», таблички для виставлення оцінок, інструкція-жестикуляція для оцінення домашнього завдання, атрибути для гри «Аукціон знань».

Хід уроку

І. Організаційний момент

1. Привітання

2. Гра в слова.

        Сьогодні ми розпочнемо урок нестандартно. Умова гри полягає в тому, що потрібно створити ланцюжок зі слів, що пов’язані з математичними термінами. Наступне слово розпочинається останньою приголосною буквою попереднього. Наприклад, математика – коло – лінійка … Учні стають в коло лицем один до одного, хто називає невірно повертається спиною. Гра продовжується доти, поки залишиться неповернутим 1 учень.

ІІ. Мотивація навчальної діяльності. Оголошення теми та мети уроку.

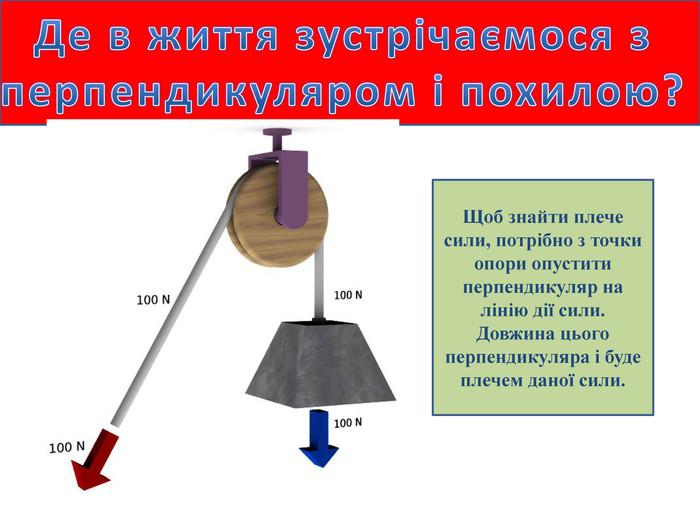
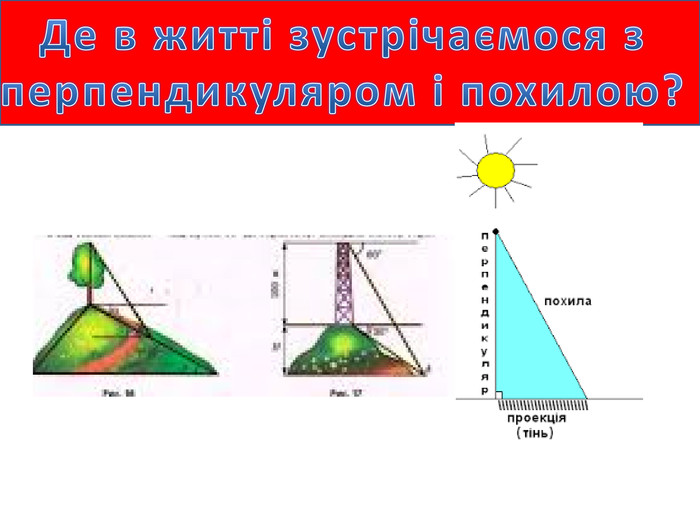
Показ картинок де в реальному житті зустрічаємося з темою уроку (слайд 2 – 4).

ІІІ. Перевірка домашнього завдання

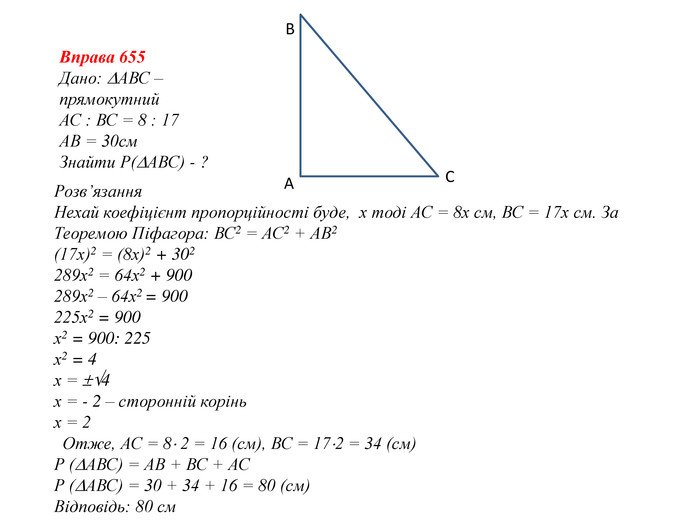
    Виводжу на екран  розв’язки домашнього завдання, а учні мовчки його перевіряють і показують знаками правильність виконання.  (слайд 5-6)

Діти оцінюють себе і заносять собі бали в таблицю оцінення.

ІV. Актуалізація опорних знань

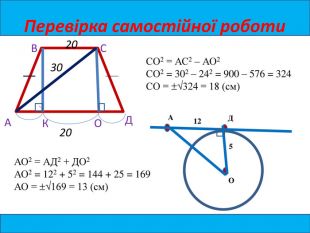
1. Самостійна робота (слайд 7 -8)

І варіант

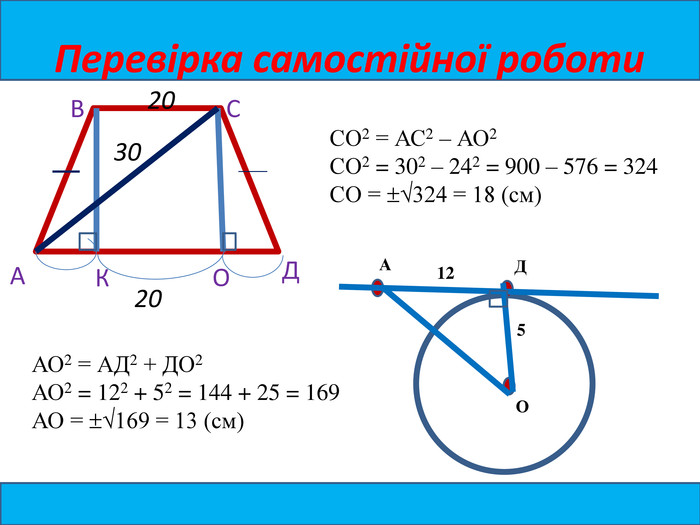
1. Основи рівнобічної трапеції дорівнюють а і в, а діагональ – с. Знайдіть висоту трапеції, якщо а = 20см, в =28см, с=30 см.
2. Із точки А до кола проведено дотичну АД (Д – точка дотику. Знайдіть відстань від точки А до центра кола, якщо радіус кола дорівнює 5 см, а довжина відрізка АД – 12 см.

 

            ІІ варіант

1.  Основи рівнобічної трапеції дорівнюють а і в, а діагональ – с.    

     Знайдіть висоту трапеції, якщо а = 16см, в =32см, с=26 см.

2. Із точки А до кола проведено дотичну АД (Д – точка дотику.   

     Знайдіть відстань від точки А до центра кола, якщо радіус кола

      дорівнює 12 см, а довжина відрізка АД – 16 см.

Взаємоперевірка (розв’язання виводиться на екран, за яким діти перевіряють правильність виконання і виставляють собі оцінку в таблицю оцінювання)

 

2. Гра «Аукціон знань» (слайд 9)

Завдання обрати аукціоніста та розіграти лот, який буде додатковим балом до самостійної роботи.

Завдання для гри:

1. Укажіть катети та гіпотенузу прямокутного трикутника, якщо його сторони дорівнюють:

1) 10см, 6см, 8см;     2) 10см, 24см, 26см.

2. Катети одного трикутника дорівнюють 5см і 12см, а другого – 12см і 16см. Гіпотенуза якого трикутників більша? Чи можна дати відповідь на запитання, не виконуючи обчислень?

3. Що називають перпендикуляром проведеним з точки до прямої? Якою геометричною фігурою є перпендикуляр?

4. Яке із наведених тверджень неправильне?

1. Довжина відрізка є додатнім числом.
2. У прямокутному трикутнику довжина гіпотенузи більша за довжину будь-якого з катетів.
3. Відстань від точки до прямої – це довжина перпендикуляра, проведеного з точки до прямої.
4. Із точки А до прямої m можна провести безліч перпендикулярів.

Учні підводять підсумки та виставляють собі оцінки в таблицю.

V. Вивчення нового навчального матеріалу (слайд 10 – 15)

Доведемо нову теорему самостійно.

Учням створюю умови для доведення теореми самостійно (опираючи на матеріали на слайдах)

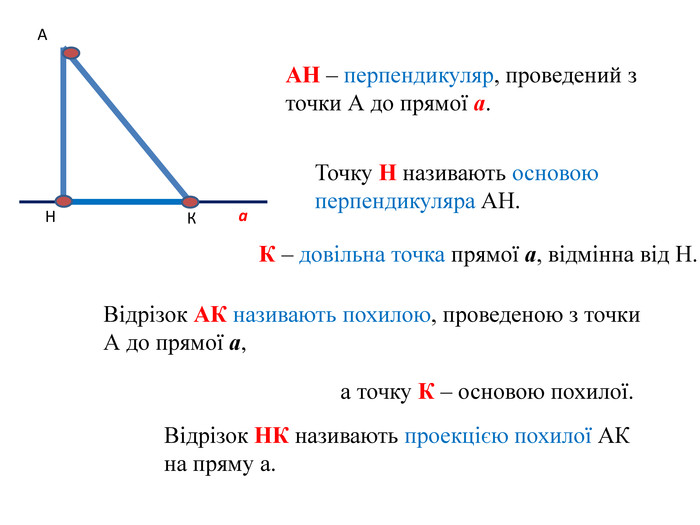
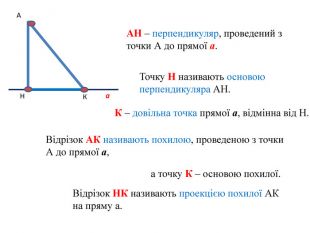
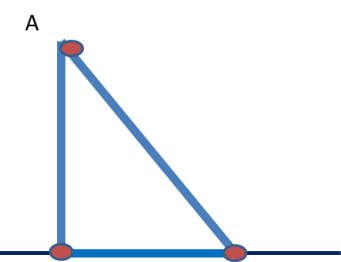
АН – перпендикуляр, проведений з точки А до прямої а.

Точку Н називають основою перпендикуляра АН.

К – довільна точка прямої а, відмінна від Н.

Відрізок АК називають похилою, проведеною з точки А до прямої а,  а точку К – основою похилої.

Відрізок НК називають проекцією похилої АК на пряму а.

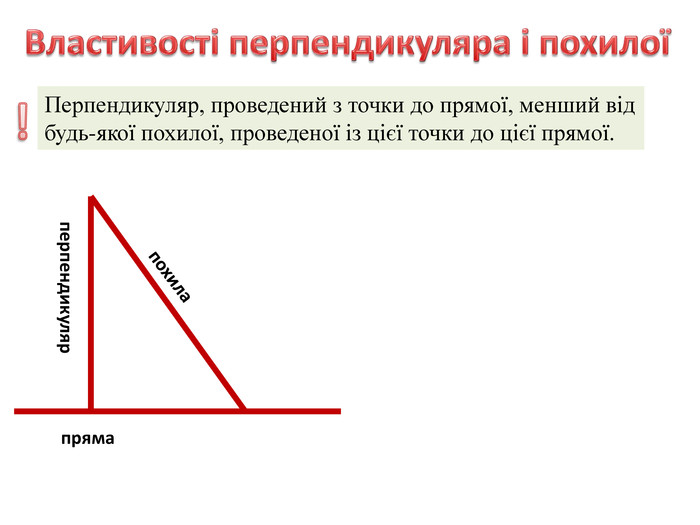
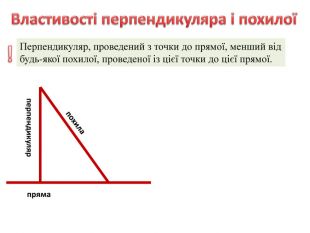
Властивості перпендикуляра і похилої

1. Перпендикуляр, проведений з точки до прямої, менший від будь-якої похилої, проведеної із цієї точки до цієї прямої.
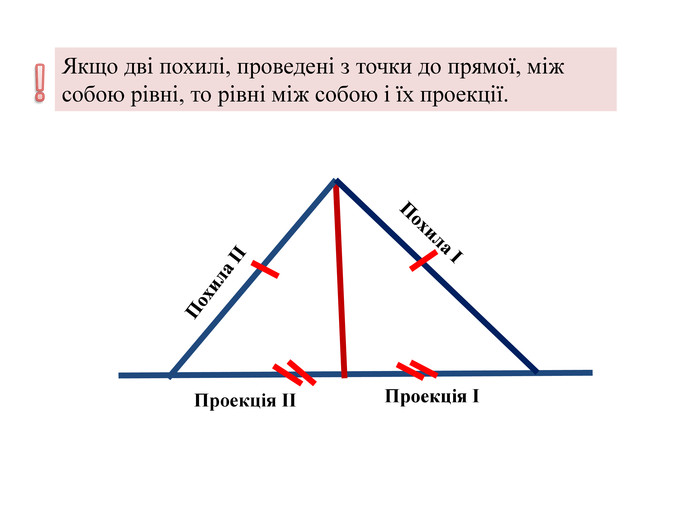
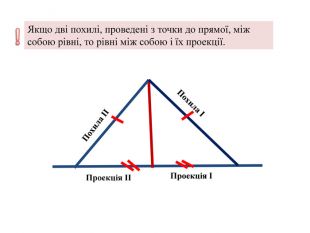
2. Якщо дві похилі, проведені з точки до прямої, між собою рівні, то рівні між собою і їх проекції.
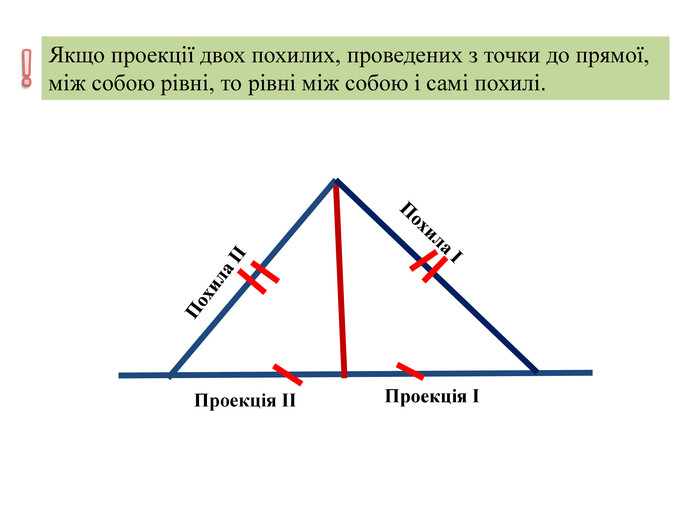
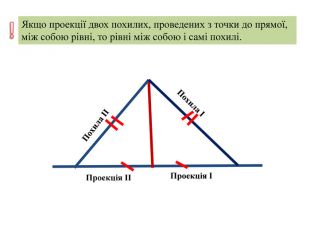
3. Якщо проекції двох похилих, проведених з точки до прямої, між собою рівні, то рівні між собою і самі похилі.
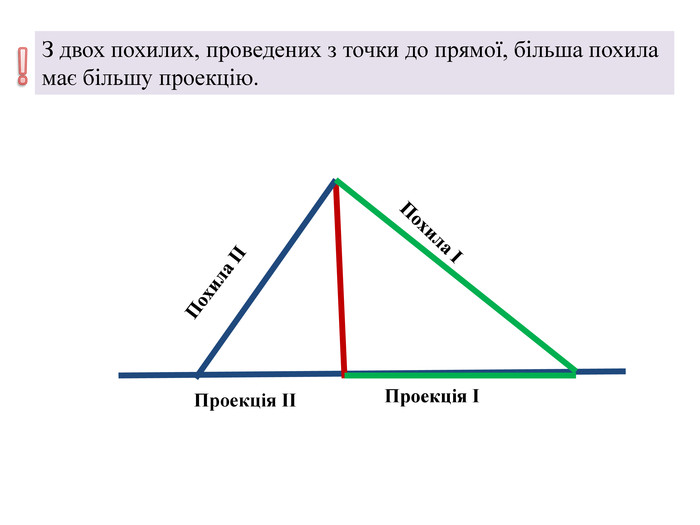
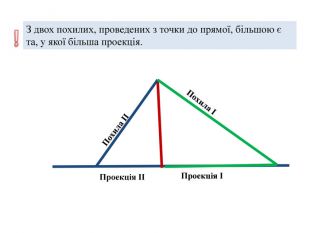
4. З двох похилих, проведених з точки до прямої, більшою є та, у якої більша проекція.
5. З двох похилих, проведених з точки до прямої, більша похила має більшу проекцію.

   VІ. Засвоєння нового навчального матеріалу

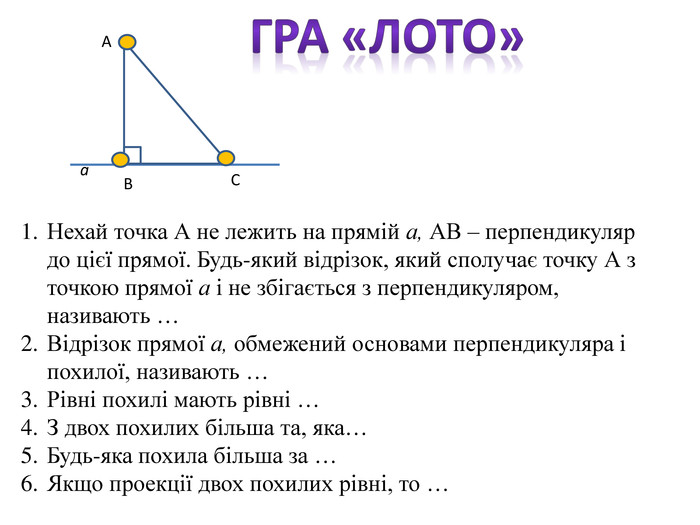
Гра «Лото»  (слайд 16)

1. Нехай точка А не лежить на прямій а, АВ – перпендикуляр до цієї прямої. Будь-який відрізок, який сполучає точку А з точкою прямої а і не збігається з перпендикуляром, називають …
2. Відрізок прямої а, обмежений основами перпендикуляра і похилої, називають …
3. Рівні похилі мають рівні …
4. З двох похилих більша та, яка…
5. Будь-яка похила більша за …
6. Якщо проекції двох похилих рівні, то …

Продовження тверджень знаходиться в учнів на парті у вигляді таблички. В комірках якої вони знаходять відповідь і ставлять на неї цифру  (порядковий номер запитання).

 

 

 

 

 

 

 

 

 

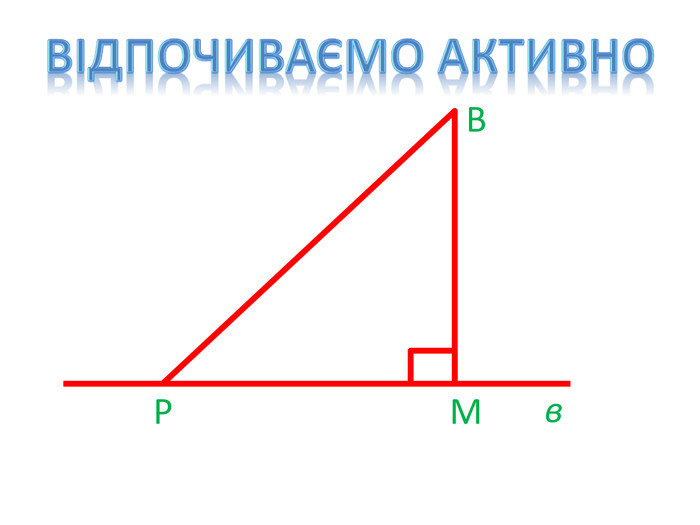
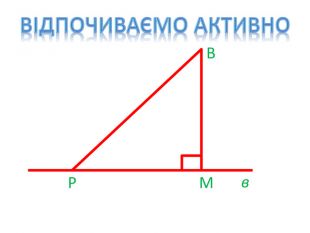
2. Відпочиваємо активно (слайд 17, 18)

  Демонструю на екрані декілька усних завдань з теми, що вивчається. Навпроти кожного завдання є дві фізичні вправи зі знаками плюс і мінус.  Якщо твердження правильне, то діти виконують фізичну вправу зі знаком плюс. Якщо ні – зі знаком мінус.

Завдання	+	-
ВР – перпендикуляр проведений з т. В до прямої в.	Присісти 3 р.	Повороти голови за годинниковою стрілкою 4р.
М – основа перпендикуляра ВМ	Вправа «Ножиці» 4р.	Стрибки вгору 4р.
ВР – похила проведена з т. В до прямої в.	Повороти тулуба вліво-вправо 3р.	Повороти тулуба вперед-назад 3р.
т. В – основа похилої	Стрибки вгору 4р.	Присісти 3р.
Відрізок РМ – проекція похилої ВР	Зробити «Ласточку»	Лівою рукою достати правої ноги і навпаки

 

 

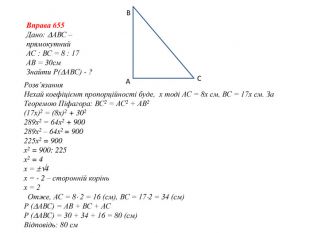
3. Розв’язування задач практичного характеру (сайт 20)

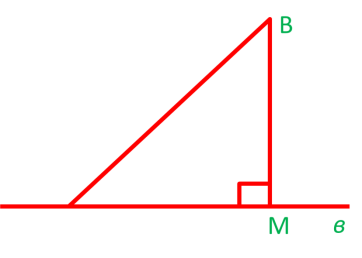
            Господар для збереження свого врожаю вирішив підв’язати огірки. Для цього він використовував дерев’яний кіл, до  якого підв’язував один кінець нитки, а інший відтягував до ямки з насінням,  для того, щоб коли проросте, змогло витися по даній тинці. В результаті від одного кола відходили нитки до двох ямок. Оскільки кіл був розміщений  не по центру, то довжина ниток до ямок була різною. До однієї ямки вона становила 30 см, до іншої 26см. Висота самого кола становила 24см. Чому дорівнює різниця відстаней від ямок до кола?

Дано: ВС = 30см

АВ =26см, ВД = 24см

Знайти: ДС – АД

Розв’язання

ДС² = ВС² – ВД²

ДС² = 900 – 576 = 324

ДС = 18

АД² = АВ² – ВД²

АД² = 676 – 576 = 100

АД = 10

ДС – АД = 18 – 10 = 8 см.

Відповідь: 8см

VII. Підведення підсумків уроку

Складання сенкану

Алгоритм написання:

1. Перший рядок має містити слово, яке позначає тему (зазвичай це іменник)
2. Другий рядок – це опис, який складається з двох слів (два прикметники)
3. Третій рядок називає дію, пов’язану з темою, і складається з трьох слів, (зазвичай це дієслова);
4. Четвертий рядок є фразою, яка складається з чотирьох слів і висловлює ставлення до теми, почуття з приводу обговорюваного;
5. Останній рядок складається з одного слова – синоніма до першого слова, у ньому висловлюється сутність теми, ніби робиться підсумок.

Похила

Проведена, більша

Вказує, визначає, має

З точки до прямої

Відрізок

2. Оцінення

Діти підраховують бали, які отримали під час уроку і виставляють собі оцінку.

Вид роботи	Д/З	С/Р	Аукціон	Лото	Фізхвилинка	Задача
Макс. бал	4	8	4	3	1	4
Набр. бал

Оцінка виставляється у відношенні 2:1, тобто, якщо учень набрав 24 бали, то його оцінка 12. і т.п.

       Урок підготувала вчитель математики Сербівської ЗШ І-ІІІ ступенів Трембовецька О.А.