Матеріали до уроку "Правильні многогранники"

Правильні многогранники

Матеріали до уроку

1. Теоретичні відомості

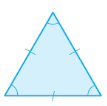
Опуклий многогранник називається правильним, якщо його грані – рівні правильні многокутники й у кожній вершині сходиться одна й та сама кількість ребер.

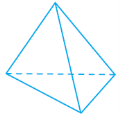
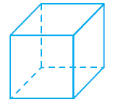
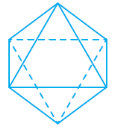
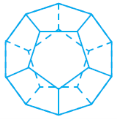
Існує п’ять видів правильних многогранників: правильний тетраедр, куб, октаедр, додекаедр та ікосаедр.

Назви тетраедр, октаедр, додекаедр, ікосаедр у перекладі з грецької означають відповідно: чотиригранник, восьмигранник, дванадцятигранник і двадцятигранник. Куб називають ще правильним гексаедром.

2. Теоретична розминка

1. Чи є правильним многогранником:

1) довільна правильна піраміда;

2) довільна правильна призма?

2. Чи існує:

1) піраміда;

2) призма,

яка є правильним многогранником?

3. Чому гранями правильного многогранника не можуть бути правильні шестикутники?

3. Вправи і задачі

1. Знайдіть площу повної поверхні куба, якщо площа однієї грані дорівнює 9см².

2. Знайдіть площу повної поверхні правильного тетраедра, ребро якого дорівнює 4см.

3. Площа поверхні ікосаедра дорівнює 80см². Знайдіть довжину ребра ікосаедра.

4. Знайдіть суму всіх плоских кутів при всіх вершинах октаедра.

5. Ребро куба дорівнює 8см. Площа поверхні додекаедра дорівнює площі повної поверхні куба. Знайдіть площу однієї грані додекаедра.