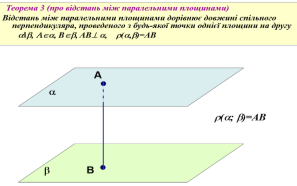
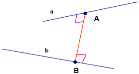
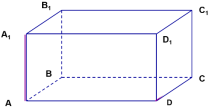
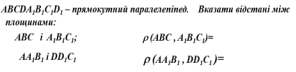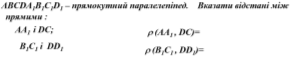Матеріали щодо організації самостійної діяльності учнів на уроці геометрії для 10-го класу до теми "Відстані у просторі"

Тема уроку: Відстані у просторі

Вивчай все не заради марнославства,

а заради практичної користі.

Г. Сковорода

Оціночна картка роботи на уроці учня

Домашнє завдання		Дешифровка (0-3,2)	Робота в парах  (0-7)	Пропуски в задачах (0-9)	Фронтальне опитування (0-7)	Самостійна робота (0-6)	Всього (0-40)
Практична  частина  (0-5)	Бліц- опитування (0-2,8)

 

Перевірка домашнього завдання

Практичний блок. Консультанти за зразком

№1^о. (за правильну відповідь 1 бал)

А	Б	В	Г
паралельні	перпендикулярні	інша відповідь	паралельні або перетинаються

 

№2^о. (за правильну відповідь 1 бал)

А	Б	В	Г	Д
DD1	AB	B1C1	DC	AB1

 

 №3^*. (за правильне рішення 3 бали)

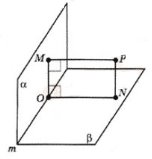
Дано: PN:PM=2:3, αβ, m – пряма перетину площин α і β, 

             P – точка простору, РО = 2см.

Знайти: PN і PM

Розв’язання:

Нехай коефіцієнт пропорційності х. Тоді ОМ=3х, PN=2x.

PM α, PM=MO=3x (см)

PNβ, PN=ON=2x (см)

За теоремою Піфагора PO=- коефіцієнт пропорційності. Отже, PM=3·2=6см, PN=2·2=4 см.

 

 

Теоретичний блок. Бліц опитування «Так – ні» (за кожну правильну відповідь по 0,2 бали)

Чи правильне твердження?

1. Через будь-яку пряму можна провести площину, перпендикулярну до заданої.

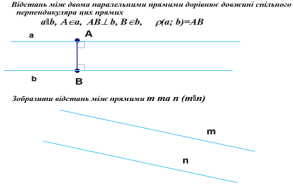
2. Якщо пряма паралельна одній з двох перпендикулярних площин, то вона перпендикулярна й до другої.

3. Якщо дві площини перпендикулярні до третьої, то вони можуть бути паралельними.

4. Якщо дві площини перпендикулярні до третьої, то вони перпендикулярні між собою.

5. Якщо пряма перетинає одну з двох перпендикулярних площин, то вона перетинає й другу

6. Якщо площина перпендикулярна до заданої площини, то вона перпендикулярна і до будь-якої прямої, паралельної цій площині.

7. Площини вертикальних діагональних перерізів куба є взаємно перпендикулярними.

8. Якщо пряма паралельна одній з двох перпендикулярних площин, то вона

паралельна і другій.

9. Через точку, взяту поза площиною, можна провести площину, перпендикулярну до цієї площини, і причому тільки одну.

10. Якщо пряма паралельна одній з двох перпендикулярних площин, то вона лежить в другій площині.

11. Якщо дві площини перпендикулярні до третьої, то вони не можуть перетинатися.

12. Якщо площина і пряма перпендикулярні до однієї й тієї самої площини, то вони паралельні між собою.

13. Якщо дві площини перпендикулярні до третьої площини, то пряма їх перетину також перпендикулярна до тієї самої площини.

14. Через перпендикуляр до заданої площини можна провести єдину площину, перпендикулярну цій площині.

 

Мотивація навчальної діяльності учнів

 

  Тема уроку з’ясовується учнями самостійно за допомогою дешифровки. (Запишіть перші літери слів, запропонованих означеннями)

 

	Буква		Буква
Частина прямої, що лежить між двома точками				Відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.
Чорна, червона, кабачкова				Результат віднімання
Хорда, що проходить через центр кола.				Паралельні сторони трапеції
Розділ геометрії, який вивчаємо				Відношення протилежного катета до гіпотенузи у прямокутному трикутнику
Твердження, що потребує доведення				Рівнобедрений . . .
Твердження, що не потребує доведення				.… координат
5-5=				Чотирикутник, всі сторони якого рівні.
Сухофрукт із винограду				М’ясо птиці, не курятина

 

Вивчення нового матеріалу

Опорний конспект

 

 

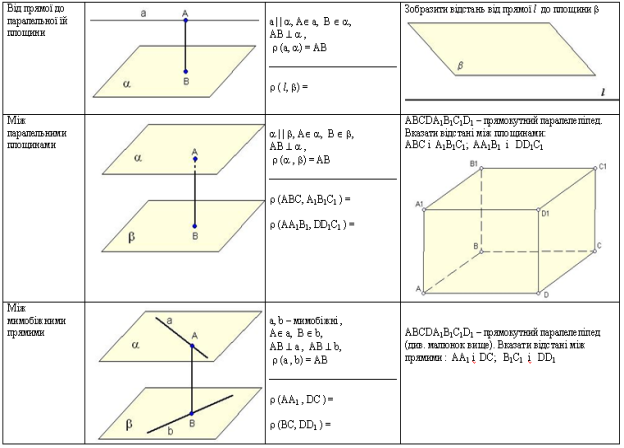
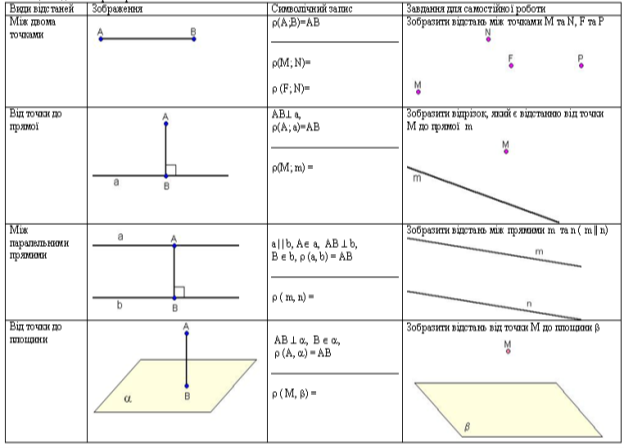
Первинне застосування придбаних знань

Робота в парах (за  кожну правильну відповідь по 0,5 бали)

 

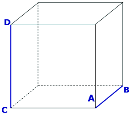
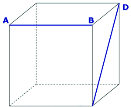
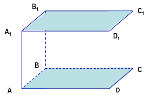
1. На зображенні куба вкажіть спільний перпендикуляр до прямих АВ і СD
2. АВСD – квадрат, МВ(АВСD). Продовжити речення:
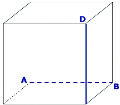
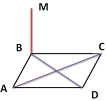
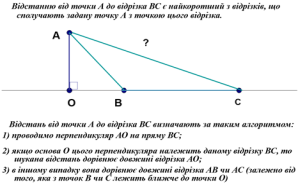
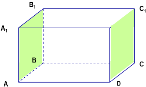
1) Відстанню від точки М до
прямої АВ  буде довжина відрізка …		прямої АD буде довжина відрізка …		прямої АС буде довжина відрізка …
2) Відстанню між прямими ВМ і  АD буде довжина відрізка …
3) Відстанню між прямими AD і DC буде довжина відрізку …
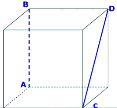
3. АBCD – прямокутник зі сторонами 6 см і 8 см, МО (АВСD), МО=4 см. Продовжити речення:
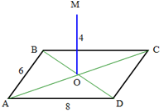
1)  Відстань між прямими МО і  АВ дорівнює …
2)  Відстань між прямими МО і  ВС дорівнює …
3)  Відстань від точки А до прямої МО дорівнює …
4)  Відстань від точки М до прямої АВ дорівнює …
5)  Відстань від точки М до точки В дорівнює …

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Застосування учнями знань і дій у стандартних умовах з метою засвоєння навичок

 

Виконаємо разом: за готовими рисунками заповнимо пропуски в рішенні

Задача 1. ( за кожен заповнений пропуск по 0,5 бали)

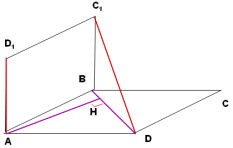Рівні прямокутники ABCD і ABC₁D₁ лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD₁ і С₁D, якщо АВ=15 см, ВС=20 см

 

Розв’язання
Оскільки D₁A і C₁В – … до прямої перетину двох перпендикулярних площин, то D₁A … (АВС), С₁В … (АВС). 
Побудуємо ортогональні проекції прямих AD₁ і С₁D на площину АВС.

Проекціями є відповідно … та … . Шукана відстань дорівнює висоті АН ΔABD (A=90⁰).
За теоремою Піфагора ВD = … см, то 

Відповідь: … см

 

Задача 2. ( за кожен заповнений пропуск по 1 балу)

Два відрізка  упираються своїми кінцями в дві паралельні площини різниця цих відрізків дорівнює 17 см а їх проекції на одну із площин дорівнюють 9 см і 42см знайти відстань між площинами.

 

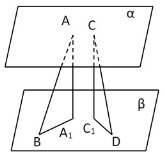Розв’язання

Нехай αβ, АВ, CD - дані відрізки, АВ – СD = 17 cм, AA₁BA₁= 42 cм, C₁D = 9 cм. 

Нехай  CD = x cм,  тоді  АВ = … см.

Із АВА_1: AA₁² = AB² - A₁B² = …

Із CC₁D: CC₁² = CD² - C₁D² = …

Враховуючи, що AA₁ = СС₁, маємо …

Отже CD = … cм, CC₁= … cм.

 

 

Творчий перенос знань і навичок у нові або змінені умови з метою формування вмінь

Самостiйна робота із взаємоперевіркою за зразком на дошці (з обґрунтуванням по 3 бали)

 

№	Варiант 1	Варiант 2
1	Пряма CD перпендикулярна площинi гострокутного трикутника ABC, CK — його висота. Доведiть, що прямi DK i AB взаємно перпендикулярнi. Знайдiть вiдстань вiд точки A до площини DKC, якщо DA = см, ∠DAK = 45º.	Діагоналі чотирикутника ABCD перетинаються в точці O. З точки O проведено перпендикуляр OM до прямої AB i перпендикуляр OK до площини чотирикутника. Доведiть, що кут між прямими MK i AB прямий. Знайдiть вiдстань вiд точки B до площини OKM, якщо KM = см, ∠MKB = 30º.
2	Площини α i β перпендикулярнi. Рівносторонній трикутник ABC лежить у площинi α так, що сторона AB належить прямій перетину площин. Пряма b лежить у площинi β, паралельна прямій перетину площин i віддалена вiд неї на 4 см. Обчисліть вiдстань вiд точки C до прямої b, якщо AB =см.	Площини α i β перпендикулярнi. Рівнобедрений трикутник ABC лежить у площинi α так, що його основа AB належить прямій перетину площин. Пряма b лежить у площинi β, паралельна прямій перетину площин i віддалена вiд неї на 5 см. Обчисліть вiдстань вiд точки C до прямої b, якщо AB = 32 см, AC = 20 см.

 

 

 

 

Підсумки уроку

Фронтальне опитування ( за кожну повну відповідь по 1балу)

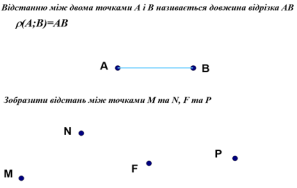
1. Дайте визначення ключового слова у всіх означеннях відстаней у просторі.

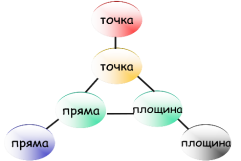2. Сформулюйте означення вiдстанi та проілюструйте кожне з них на відповідних моделях або предметах навколишнього середовища:

а) від точки до прямої;

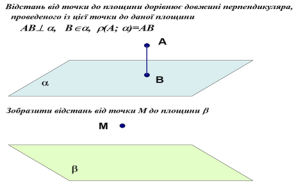
б) від точки до площини;

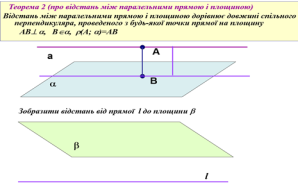
в) від прямої до площини;

г) між площинами;

д) між паралельними прямими;

е) між мимобіжними прямими.

 

Рефлексія

1. Чи досягли ви на уроці очікуваних результатів?

2. Що нового дізналися на уроці?

3. Що було найскладнішим під час виконання завдань?

4. Що було головним на уроці? Чому навчилися?

 

Оцінювання навчальних досягнень учнів

Таблиця переводу отриманих балів

Набрані бали	40-38	37-35	34-31	30-27	26-23	22-18	17-13	12-9
Оцінка	11	10	9	8	7	6	5	4

Повідомлення домашнього завдання

І. Теоретична частина

           Вивчити  за опорним конспектом

         ІІ. Практична частина

1.Точка S віддалена від вершин квадрата зі стороною см на 2 см. Чому дорівнює відстань від точки S  до площини квадрата?

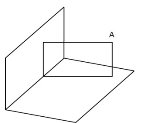    2. Точка А знаходиться на відстані 6 і 8 см від двох перпендикулярних площин (див. рис.). Знайдіть відстань від цієї точки до лінії перетину площин.

3^*. Скласти сенкан із словом «відстань»

 

 

 

 

 

Якщо ти пропустив урок …