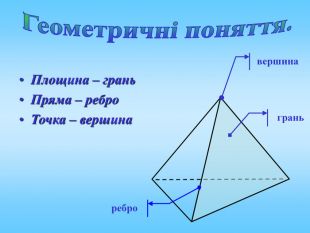
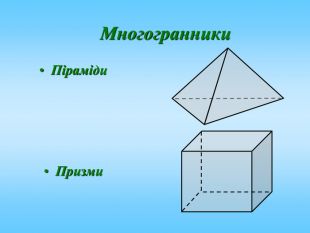
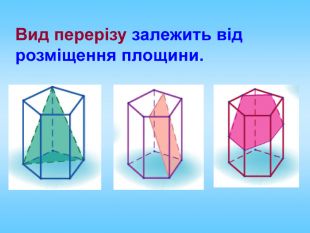
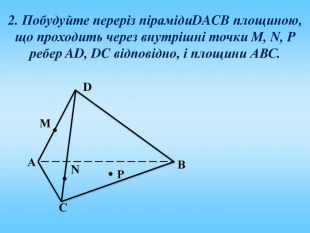
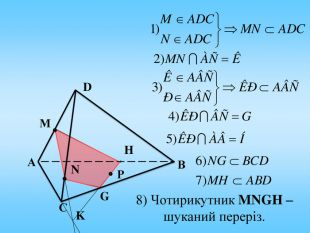
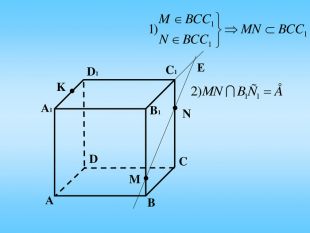
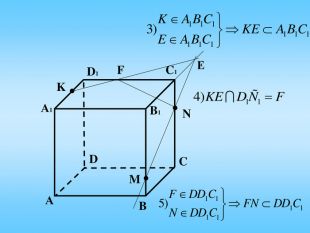
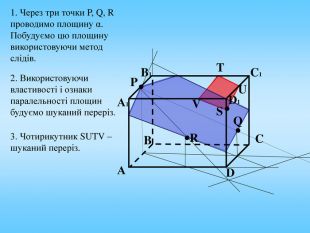
Проект до уроку геометрії в 10 класі "Побудова перерізів многогранників"

Підготували: Учні 10 класу, Маломихайлівського НВК І-ІІІ ступенів імені І.Г.Скакуна

Мета: Повторити геометричні поняття і твердження;дослідити методи побудови перерізів, навчитися будувати їх різними способами; розвивати просторову уяву та вміння логічно вибудовувати своє пояснення, розкрити практичне значення перерізів.

Геометричні поняття; Геометричні твердження; Методи побудови перерізів; Практичне значення перерізів ; Література; Побудови перерізів;

Чи можна , володіючи знаннями учня – десятикласника дослідити закони побудови споруд і їх конструкцій?

грань ребро вершина Площина – грань Пряма – ребро Точка – вершина

Многогранники Піраміди Призми

Якщо дві точки прямої лежать на одній площині, то і вся пряма належить даній площині.

Якщо дві паралельних площини перетинаються третьою площиною, то лінії їх перетину паралельні.

Вид перерізу залежить від розміщення площини.

Основні поняття. Січною площиною многогранника називається така площина по обидві сторони від якої є точки даного многогранника. Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини

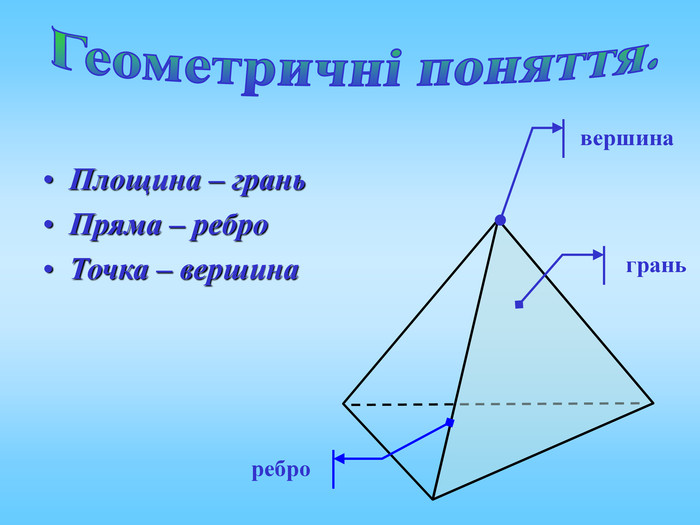
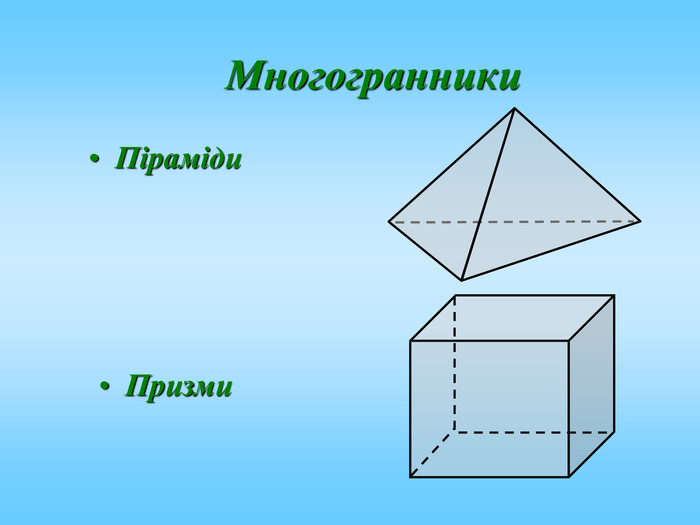
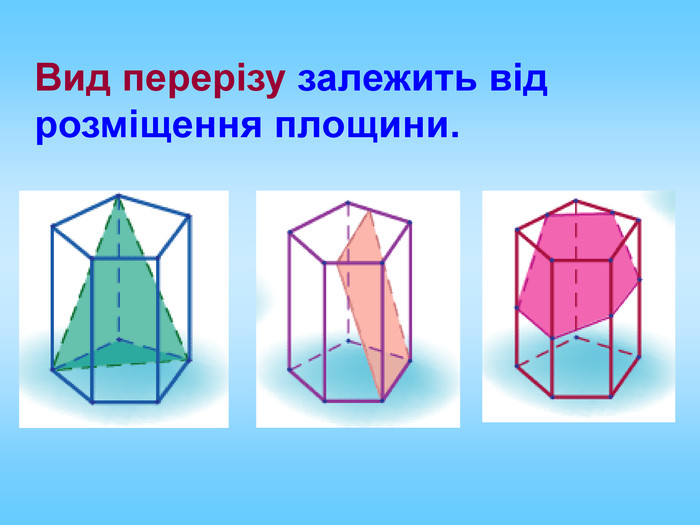
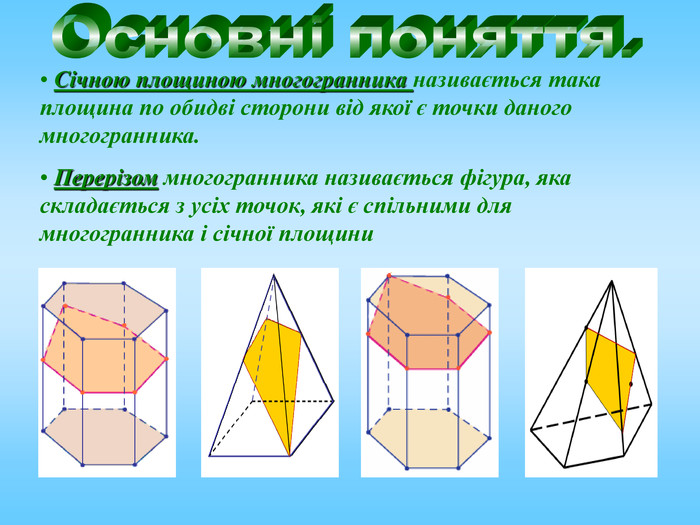
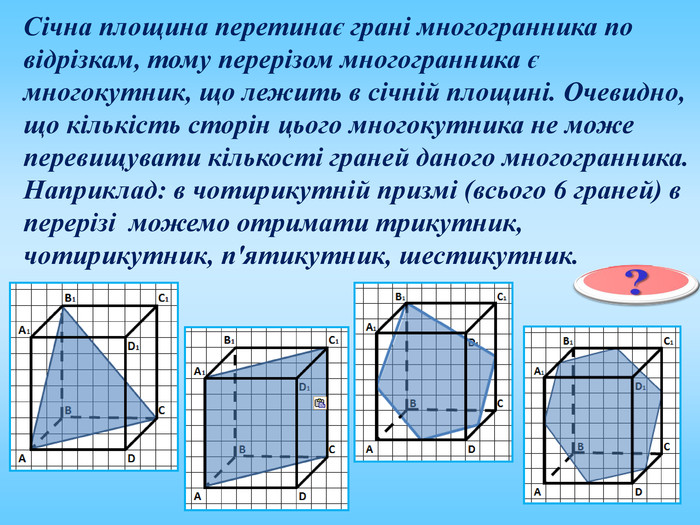
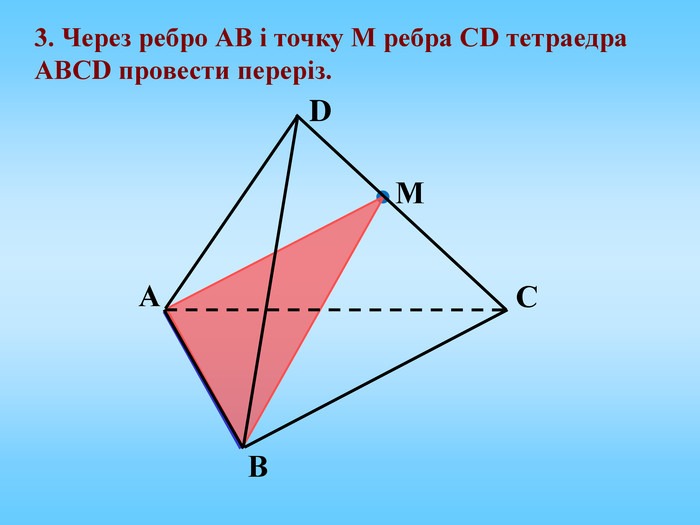
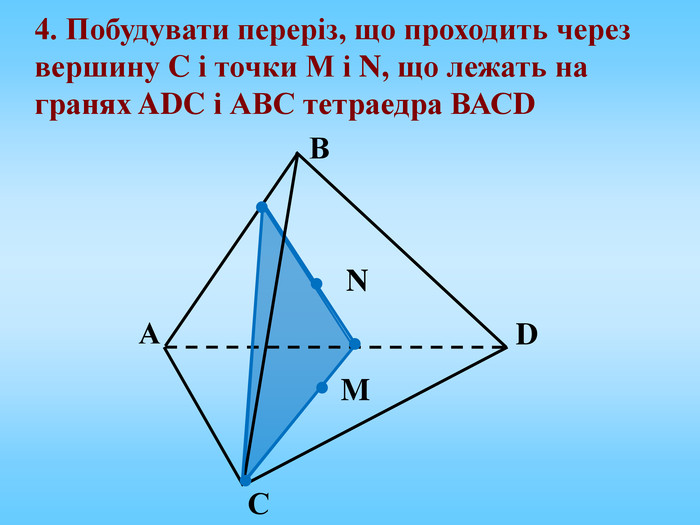
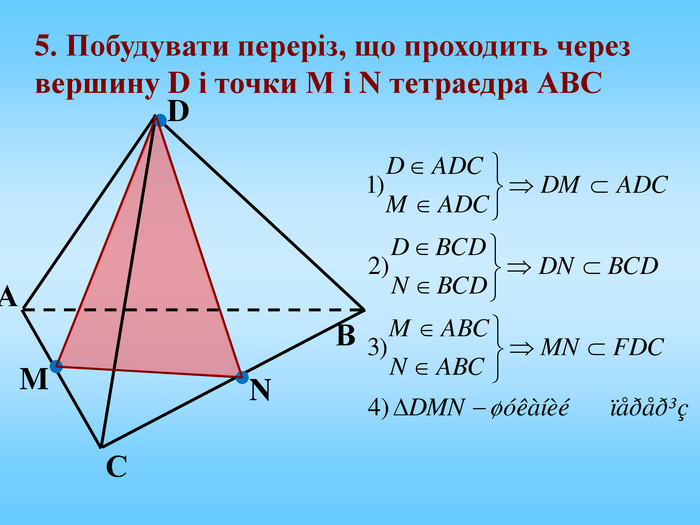
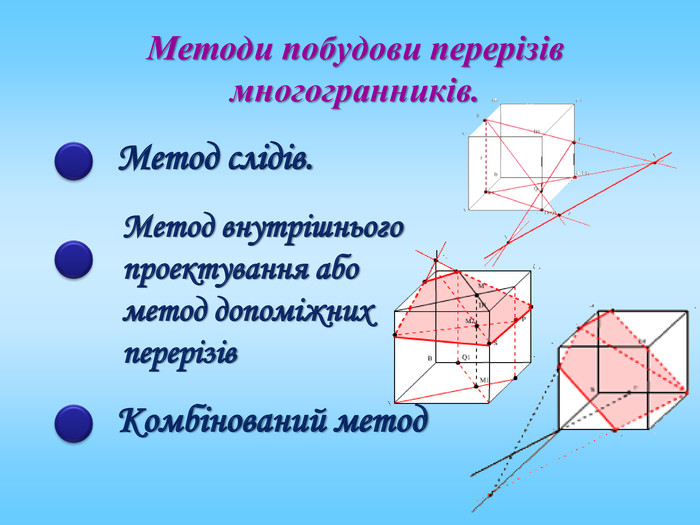
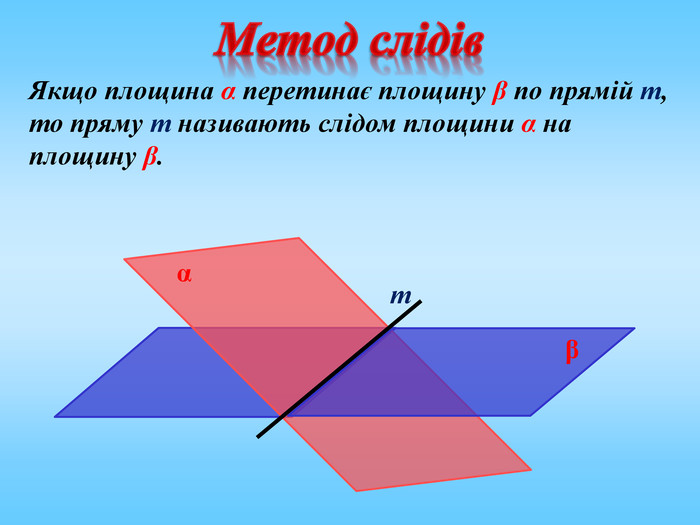
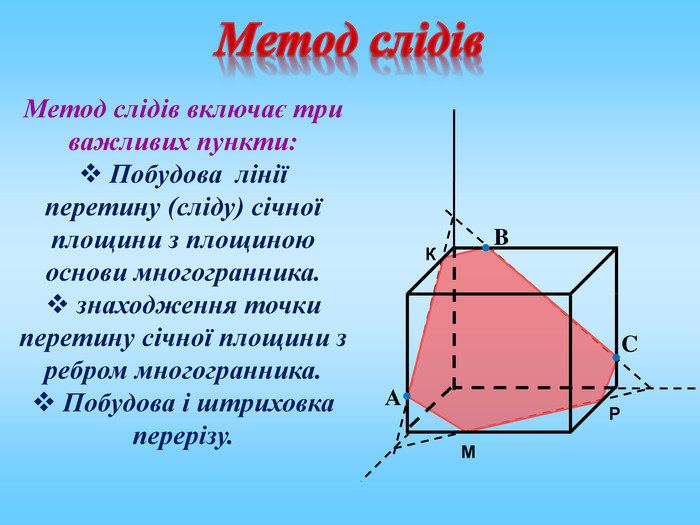
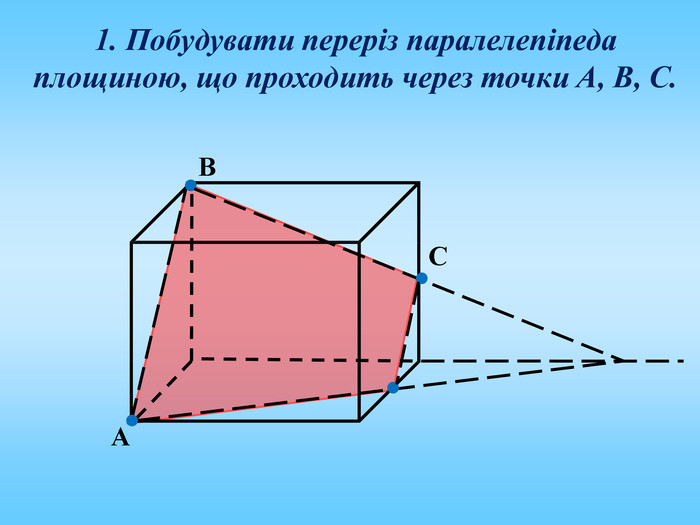
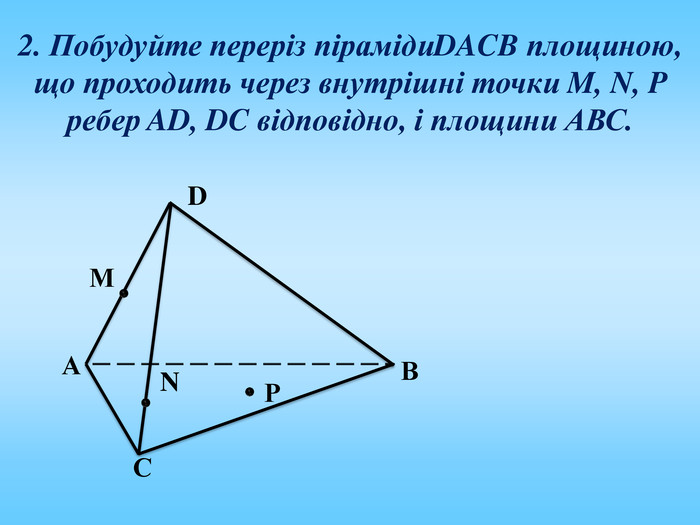
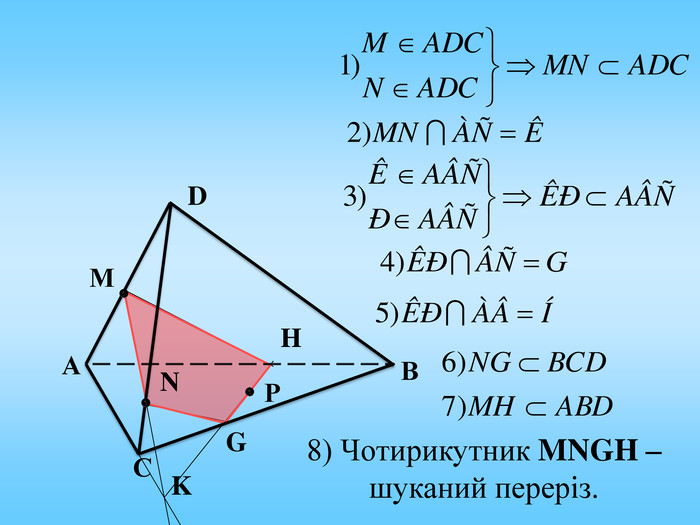
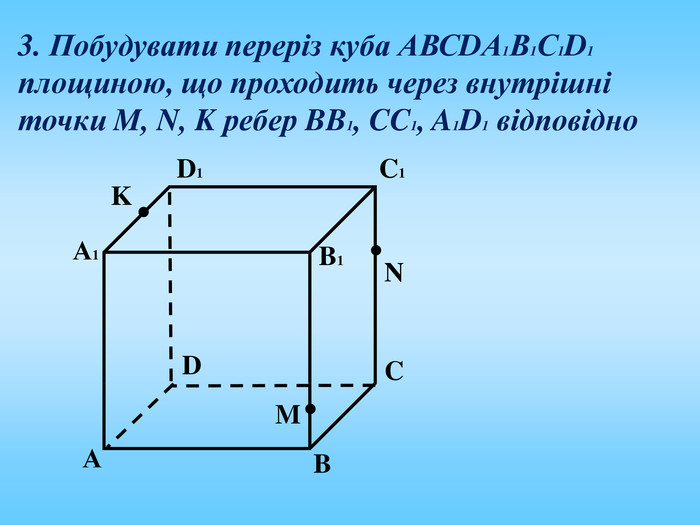
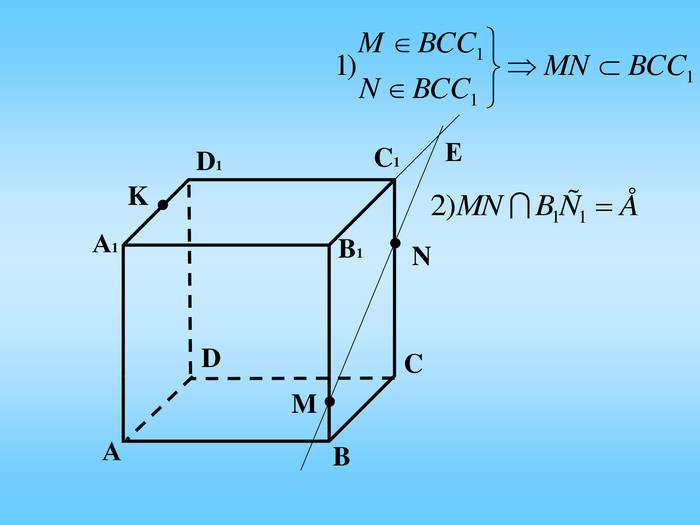
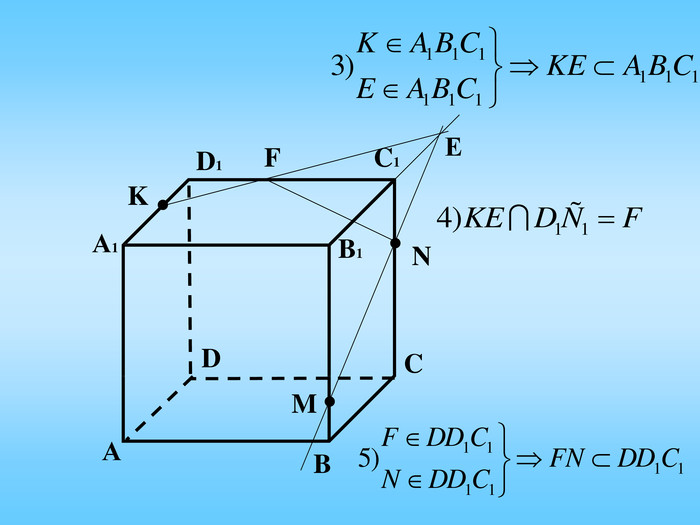
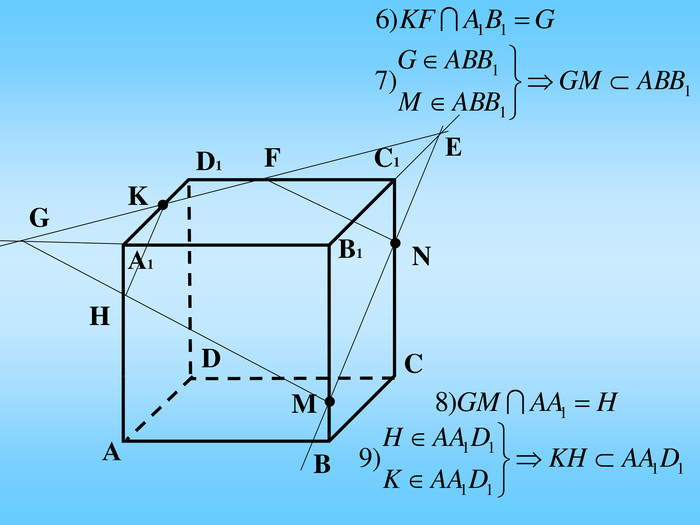
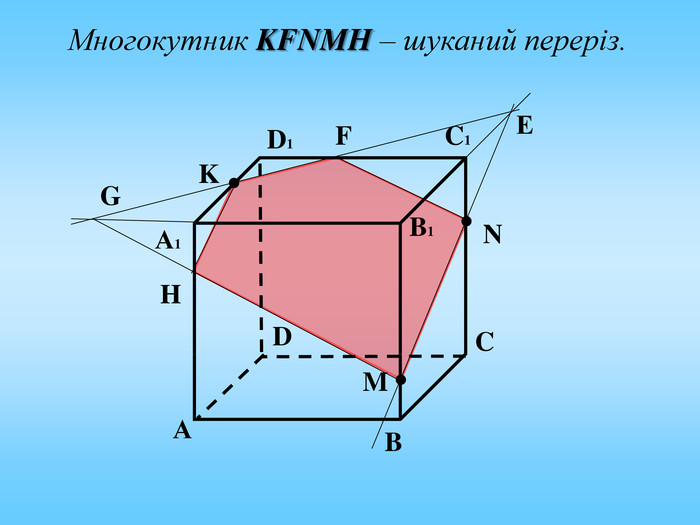
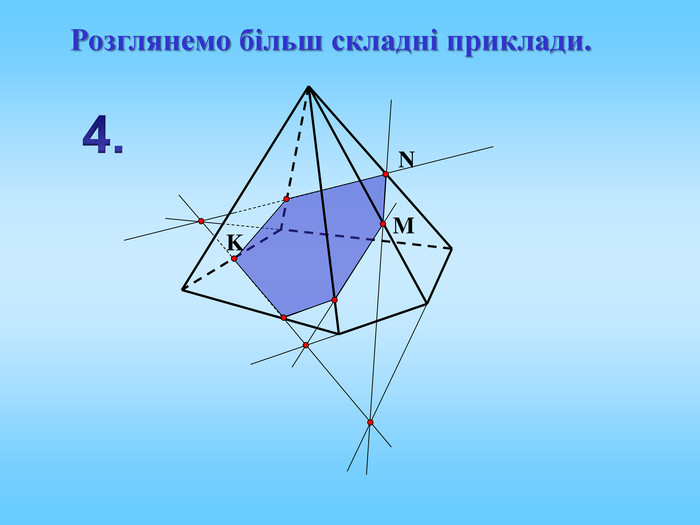
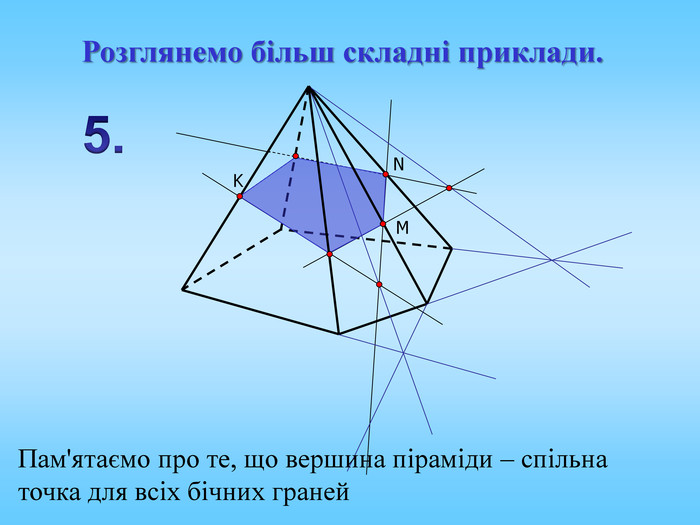
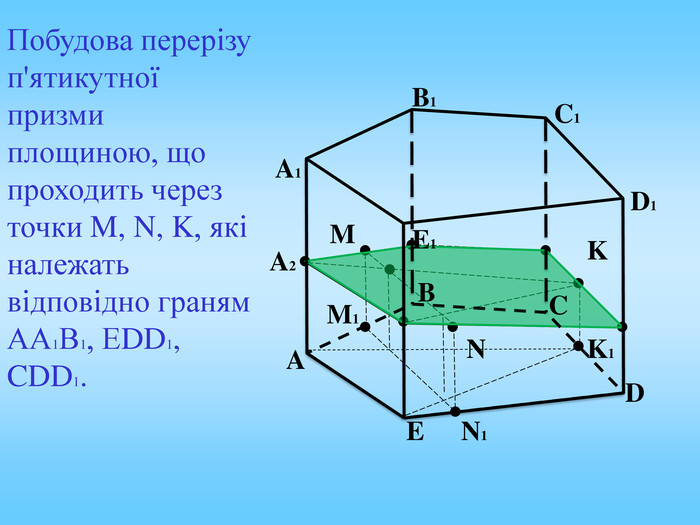
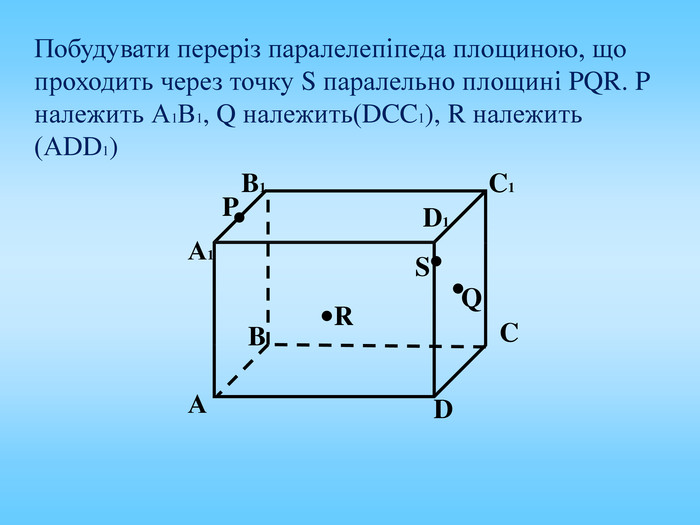
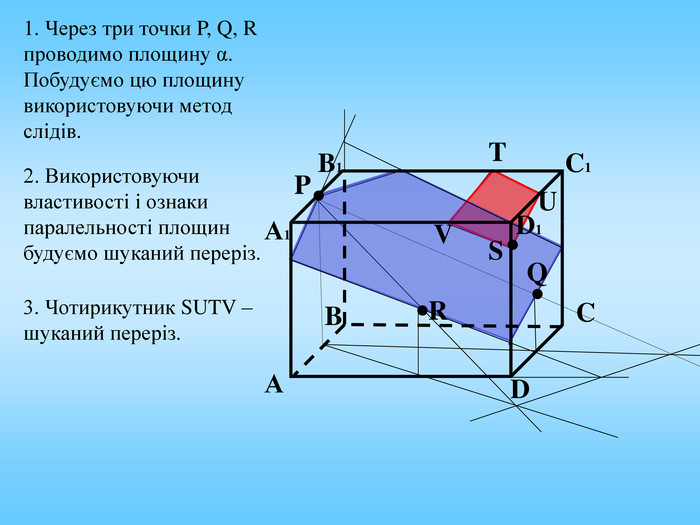
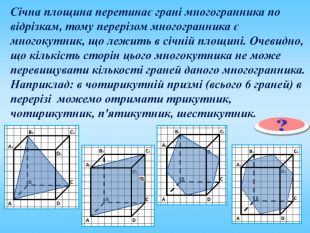
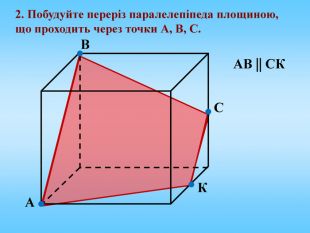
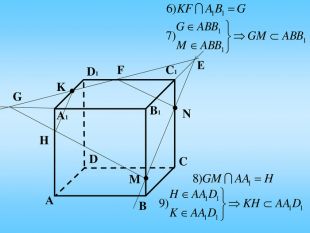
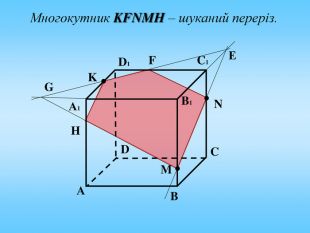
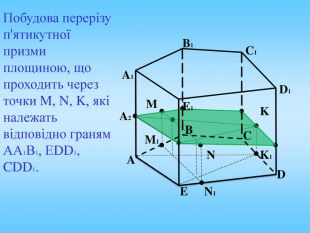
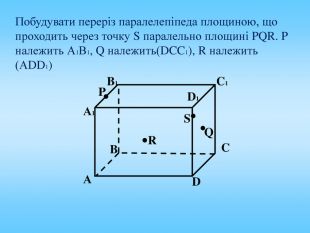
Січна площина перетинає грані многогранника по відрізкам, тому перерізом многогранника є многокутник, що лежить в січній площині. Очевидно, що кількість сторін цього многокутника не може перевищувати кількості граней даного многогранника. Наприклад: в чотирикутній призмі (всього 6 граней) в перерізі можемо отримати трикутник, чотирикутник, п'ятикутник, шестикутник.

Що означає побудувати переріз? Побудувати переріз многогранника площиною – означає: в площині кожної перетнутої грані вказати дві точки, що належать перерізу; з'єднати ці точки прямою; знайти точки перетину прямої з ребрами многогранника.

1. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С. А В С

А В С 2. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С. К АВ || СК

3. Через ребро АВ і точку М ребра СD тетраедра АВСD провести переріз. М А В С D

А С D В 4. Побудувати переріз, що проходить через вершину C і точки М і N, що лежать на гранях ADC і АВС тетраедра ВАСD N M

А С В D 5. Побудувати переріз, що проходить через вершину D і точки М і N тетраедра АВС N M

Методи побудови перерізів многогранників. Метод слідів. Метод внутрішнього проектування або метод допоміжних перерізів Комбінований метод

Якщо площина α перетинає площину β по прямій т, то пряму т називають слідом площини α на площину β. α β т

Метод слідів включає три важливих пункти: Побудова лінії перетину (сліду) січної площини з площиною основи многогранника. знаходження точки перетину січної площини з ребром многогранника. Побудова і штриховка перерізу. М C B А К Р

1. Побудувати переріз паралелепіпеда площиною, що проходить через точки А, В, С. А С В

2. Побудуйте переріз пірамідиDACB площиною, що проходить через внутрішні точки M, N, P ребер AD, DC відповідно, і площини АВС. А N М Р D С В

А N М Р D С В K H G 8) Чотирикутник MNGH – шуканий переріз.

3. Побудувати переріз куба АВСDА1В1С1D1 площиною, що проходить через внутрішні точки M, N, K ребер BB1, CC1, A1D1 відповідно А C B D А1 D1 C1 B1 K N M

А C B D А1 D1 C1 B1 K N M Е

А C B D А1 D1 C1 B1 K N M Е F

А C B D А1 D1 C1 B1 K N M Е F G H

А C B D А1 D1 C1 B1 K N M Е F G H Многокутник KFNMH – шуканий переріз.

M N K Розглянемо більш складні приклади.

M N K Пам'ятаємо про те, що вершина піраміди – спільна точка для всіх бічних граней Розглянемо більш складні приклади.

M Метод внутрішнього проектування X Y A A1 N M1 N1 T D1=T1 B C D E E1 C1 B1 Це метод використовується при побудові перерізів в тих випадках, коли незручно знаходити слід січної площини, наприклад, слід знаходиться дуже далеко від заданої фігури

Побудова перерізу п'ятикутної призми площиною, що проходить через точки M, N, K, які належать відповідно граням АА1В1, ЕDD1, CDD1. A C B M D E A1 C1 B1 D1 E1 K N M1 N1 K1 A2

Комбінований метод. При побудові перерізу цим методом використовуються прийоми: метод слідів метод внутрішнього проектування, теореми про паралельність прямих і площин!

Побудувати переріз паралелепіпеда площиною, що проходить через точку S паралельно площині PQR. P належить А1В1, Q належить(DCC1), R належить (АDD1) Q P R B А D C B1 А1 C1 D1 S

B А D C B1 А1 C1 D1 1. Через три точки P, Q, R проводимо площину α. Побудуємо цю площину використовуючи метод слідів. Q P R S 2. Використовуючи властивості і ознаки паралельності площин будуємо шуканий переріз. V T U 3. Чотирикутник SUTV – шуканий переріз.

Ісааківський собор Санкт-Петербург

Єгипетські піраміди Замок Нововавилонський “Каролінгський ренесанс” Рим Храм в м. Новгороді Собор в Німеччині Храм Вознесення с. Коломенське

Сучасні споруди