Матеріали щодо організації самостійної діяльності учнів на уроці геометрії для 10-го класу на тему "Перпендикулярність площин"

Про матеріал

В процесі організації самостійної діяльності учнів на уроках удосконалюється здатність учнів формулювати думки і робити висновки, розвивати свої творчі здібності, обґрунтовувати, доводити те або інше положення.

Перегляд файлу

Тема уроку: Перпендикулярність площин

Об'єкт математики настільки серйозний,

що слід не пропускати нагоди зробити

його трохи цікавішим

Б. Паскаль

Оціночна картка роботи на уроці учня

Бліц- опитування (0-4,5)

Робота в групах (0-6)

Задача за малюнком (0-2,5)

Фронтальне опитування та поточні відповіді (0-6)

Самостійне розв’язування задачі (0-3)

Всього

(0-22)

Актуалізація опорних знань

*Взаємне розміщення двох прямих у просторі*
$C:\Users\sergey pronenko\Desktop\2.jpg$		$C:\Users\sergey pronenko\Desktop\3.jpg$		$C:\Users\sergey pronenko\Desktop\4.jpg$
*Взаємне розміщення прямої і площини*
$C:\Users\sergey pronenko\Desktop\5.jpg$	$C:\Users\sergey pronenko\Desktop\6.jpg$		$C:\Users\sergey pronenko\Desktop\7jpg.jpg$
*Взаємне розміщення двох площин у просторі*

Бліц-опитування - аналіз розміщення прямих і площин у просторі за готовими рисунками (за кожну правильну відповідь 0,5 бали)

Мотивація вивчення теми

Проблемне запитання: Наведіть приклад перетину площин у кабінеті. Як на вашу думку розміщенні дані площини? А як перевірити, що дані площини перпендикулярні?

Сприйняття й первинне усвідомлення учнями нового матеріалу

Опорний конспект

*Поняття перпендикулярних площин*
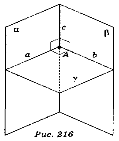
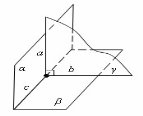
Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, проведена перпендикулярно до лінії перетину цих площин, перетинає їх по перпендикулярних прямих.		α β, бо площини α і β перетинаються по прямій с, площина γ, перпендикулярна до с, перетинає α і β по прямих а і b, які перпендикулярні.
*Ознака перпендикулярності площин*
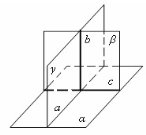
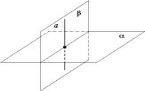
*Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.*		Дано: , , , , Довести: Доведення: Нехай і перетинаються по прямій с, а пряма с перетинається з в точці А. Через точку А в площині проведемо пряму а, . Через і проведемо площину , отже, . Оскільки , то .
*Властивість*
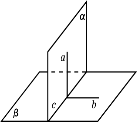
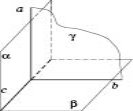
Якщо пряма, що лежить в одній із двох перпендикулярних площин, перпендикулярна до лінії їх перетину, то вона перпендикулярна й до другої площини.		, α перетинає β по прямій с і (а лежить у β), то
*Опорні факти*
Будь-яка площина, що перпендикулярна до лінії перетину двох перпендикулярних площин, перетинає їх по перпендикулярних прямих.		, α перетинає β по прямій с, γ перетинає α по а і γ перетинає β по , причому , то
*Якщо в площині є хоча б одна пряма, перпендикулярна другій площині, то ці площини взаємно перпендикулярні.*		, то .
Якщо кожна з двох площин, що перетинаються, перпендикулярна до третьої площини, то лінія перетину перших площин перпендикулярна до третьої площини.		і перетинаються по прямій с, , , то .
*Зверніть увагу!*
Щоб через пряму, що не лежить у деякій площині, провести площину, перпендикулярну даній, треба із довільної точки заданої прямої опустити перпендикуляр на площину і через цей перпендикуляр провести площину. Одержана площина буде перпендикулярною до даної.
Усі прямі, що перпендикулярні заданій площині, і перетинають деяку пряму, лежать в одній площині, перпендикулярній даній площині.
Якщо дві площини перпендикулярні, то пряма, яка є перпендикулярною до однієї із цих площин і проходить через їх спільну точку, обов’язково буде лежати в другій площині.
Через точку поза площиною можна провести безліч площин, перпендикулярних до цієї площини. (Але всі вони пройдуть через перпендикулярну до цієї площини пряму, яка проходить через дану точку.)

Ось і відповідь на поставлену проблему

Висновок: щоб обґрунтувати перпендикулярність двох площин, треба з

найти в одній із них пряму, перпендикулярну до лінії перетину площин.

Осмислення об'єктивних зв'язків і відносин у розглянутому матеріалі й розкриття внутрішньої сутності досліджуваних явищ

Робота в групах (за представлену обґрунтовану відповідь 1 бал)

Група 1	1.	Наведіть два приклади моделей перпендикулярних площин із оточення.
	2.	Дано дві перпендикулярні площини і та пряму с, яка перпендикуляр-на до площини . Укажіть, які з тверджень правильні, а які - ні .
		а) пряма с обов'язково належить площині		б) пряма с може бути паралельною площині	в) якщо пряма с належить площині , то вона паралельна лінії перетину площин і		г) будь-яка площина, яка містить пряму с, перпендикулярна до площини .
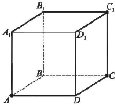
Група 2	1.	Покажіть на моделі прямокутного паралелепіпеда перпендикулярні грані (площини).
	2.	Дано зображення куба . Укажіть площини, які перпендикулярні до площини: а) АВС; б) ; в) )
Група 3	1.	На двох перпендикулярних площинах вибрали по прямій. Чи може статися, що ці прямі:
		а) паралельні	б) перетинаються		в) мимобіжні
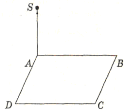
	2.	АВСD - квадрат, Запишіть площини, які перпендикулярні: а) до площини SАВ; б) до площини SАD; в) до площини SВС; г) до площини АВС; д) до площин SАВ і АВС.
Група 4	1.	Як на практиці встановити, чи перпендикулярна площина стіни до площини підлоги?
	2.	Чи правильні твердження:
		а) через точку, взяту поза площиною, можна провести площину, перпендикулярну до цієї площини, і притому тільки одну;			б) якщо площина перпендикулярна до даної площини, то вона перпендикулярна і до довільної прямої, паралельної цій площині?
Група 5	1.	Дано куб . Враховуючи, що ребра куба, які виходять з однієї вершини, попарно перпендикулярні, укажіть серед наведених тверджень правильні:

	2.	Скільки площин, перпендикулярних до даної площини, можна провести через точку поза площиною?
		А) одну	2) безліч		3) три	4) жодної

Виконаємо разом: за готовим рисунком заповнимо пропуски в рішенні ( за кожен заповнений пропуск по 0,5 бали)

Задача. З точок P і Q, які лежать на двох взаємно перпендикулярних площинах, проведено перпендикуляри PH і QC на пряму перетину площин α і β. Знайдіть довжину відрізка PQ, якщо PH=6 см, QC =7 см, HC=6 см.

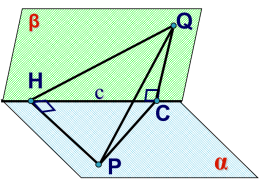Розв’язання.

Оскільки α β, РН α , РНс, то … β , звідси … HQ. Тоді ∆PHQ – … .

На площині β ∆QСH – прямокутний, оскільки QC … , то QC … .

З ∆QСH: HQ2= QС2 + HС2=49+36=85.

З ∆РHQ: РQ2= РН2 + HQ2=36 +85 =121. Враховуючи, що РQ>0, РQ =11 см.

Відповідь: 11см

Узагальнення й систематизація знань

Фронтальне опитування ( за кожну відповідь по 1 балу)

Які площини називаються перпендикулярними?
Сформулюйте ознаку перпендикулярності площин.
Як розташована пряма, яка лежить в одній із двох перпендикулярних площин і перпендикулярна до лінії перетину цих площин, відносно другої площини?

Самостійне розв’язання задачі із самоперевіркою за зразком викладача (з обґрунтуванням 3 бали)

Задача. Площини квадратів АВСD і АВ₁С₁D перпендикулярні. СD = см. Обчислити відстань між точками С і С_1.

Підведення підсумків уроку

Рефлексія

- Яке враження у Вас склалося? (Сподобалося - не сподобалося)

- Який настрій після уроку? (Радісний - сумний)

- Яке самопочуття? (Втомився - не втомився)

- Яке ставлення до вивченого матеріалу? (Зрозумів - не зрозумів)

- Яка твоя самооцінка після уроку? (Задоволений - не задоволений)

- Оціни свою активність на уроці. (Старався - не намагався).

Оцінювання навчальних досягнень учнів

Таблиця переводу отриманих балів

*Набрані бали*	*22-21*	*20-19*	*18-17*	*16-15*	*14-13*	*12-11*	*10-9*	*8-7*
*Оцінка*	11	10	9	8	7	6	5	4

3d-model-domika Повідомлення домашнього завдання

І. Теоретична частина

Вивчити за опорним конспектом

ІІ. Практична частина

№1^о. Площина α перпендикулярна до прямої b, а пряма b перпендикулярна до площини φ. Яке взаємне розміщення площин α і φ?

А	Б	В	Г
паралельні	перпендикулярні	інша відповідь	паралельні або перетинаються

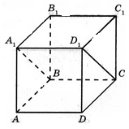
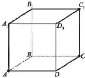
$C:\Users\sergey pronenko\Desktop\111.jpg$ №2^о. На рисунку зображено куб ABCDA₁B₁C₁D_1.Укажіть пряму, перпендикулярну до площини A₁D₁CB.

А	Б	В	Г	Д
DD₁	AB	B₁C₁	DC	AB₁

№3^*. Відстані від точки М до кожної з двох перпендикулярних площин пропорційні числам 2 і 3. Знайдіть ці відстані, якщо точка М віддалена від лінії перетину площин на 2 см.

Якщо ти пропустив урок …

Опрацюй опорний конспект
Спробуй самостійно виконати завдання

1.	αβ. Як можуть бути розташовані пряма а і площина β, якщо: а) пряма а паралельна площині α; б) пряма а належить площині α; в) пряма а перпендикулярна до площини α; г) пряма а і площина α перетинаються, але вони не перпендикулярні?
2.	α β. Як розташовані площини β і γ, якщо: а) площини α і γ перпендикулярні; б) площини α і γ паралельні; в) площини α і γ перетинаються, але вони не паралельні?
3.	Відміть «+» правильні твердження, «-» - неправильні
3.1	Через будь-яку пряму можна провести площину, перпендикулярну до заданої.
3.2	Якщо пряма паралельна одній з двох перпендикулярних площин, то вона перпендикулярна й до другої.
3.3	Якщо дві площини перпендикулярні до третьої, то вони можуть бути паралельними.
3.4	Якщо дві площини перпендикулярні до третьої, то вони перпендикулярні між собою.
3.5	Якщо пряма перетинає одну з двох перпендикулярних площин, то вона перетинає й другу
3.6	Якщо площина перпендикулярна до заданої площини, то вона перпендикулярна і до будь-якої прямої, паралельної цій площині.
3.7	Площини вертикальних діагональних перерізів куба є взаємно перпендикулярними.
3.8	Якщо пряма паралельна одній з двох перпендикулярних площин, то вона паралельна і другій.
3.9	Через точку, взяту поза площиною, можна провести площину, перпендикулярну до цієї площини, і причому тільки одну.
3.10	Якщо пряма паралельна одній з двох перпендикулярних площин, то вона лежить в другій площині.
3.11	Якщо дві площини перпендикулярні до третьої, то вони не можуть перетинатися.
3.12	Якщо площина і пряма перпендикулярні до однієї й тієї самої площини, то вони паралельні між собою.
3.13	Якщо дві площини перпендикулярні до третьої площини, то пряма їх перетину також перпендикулярна до тієї самої площини.
3.14	Через перпендикуляр до заданої площини можна провести єдину площину, перпендикулярну цій площині.

Середня оцінка розробки

Структурованість

4.0

Оригінальність викладу

4.0

Відповідність темі

4.5

Загальна:

4.2

Всього відгуків: 2

Оцінки та відгуки

Хворост Сергій 22.02.2018 в 13:20

Загальна:

4.3

Структурованість

4.0

Оригінальність викладу

4.0

Відповідність темі

5.0
Дудніченко Марина Олександрівна 16.02.2018 в 11:10

Загальна:

4.0

Структурованість

4.0

Оригінальність викладу

4.0

Відповідність темі

4.0