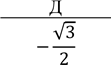Матеріали ЗНО з алгебри по темам
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ЛІНІЙНІ РІВНЯННЯ
Завдання з вибором однієї правильної відповіді Якому з наведених проміжків належить корінь рівняння ![]() 𝑥 = 1 № 11, 2021д 9−𝑥 2
𝑥 = 1 № 11, 2021д 9−𝑥 2
|
А |
Б |
В |
Г |
Д |
|
(−∞; −5] |
(−5; −2] |
(−2; 2] |
(2; 5] |
(5; +∞) |
Укажіть корінь рівняння 1 − 5𝑥 = 0 № 4, 2021
|
А |
Б |
В |
Г |
|
5 |
|
|
4 |
Яке з наведених чисел є коренем рівняння ![]() ? № 4, 2020
? № 4, 2020
|
|
А |
Б |
В |
Г |
Д |
|
|||||||
|
|
1 |
0 |
3 |
–2 |
–1 |
|
|||||||
|
|
|
||||||||||||
|
Якому з проміжку належить корінь рівняння 2𝑥 − 3 = 4. |
№ 5, 2018д |
||||||||||||
|
|
А |
Б |
В |
Г |
Д |
|
|||||||
|
|
(−∞; −2) |
[−2; 0) |
[0; 2) |
[2; 4) |
[4; +∞) |
|
|||||||
Укажіть проміжок, якому належить корінь рівняння 0,5(𝑥 − 4) = 1,5. № 2, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
(–∞; –4] |
(–4; 0] |
(0; 4] |
(4; 8) |
(8; +∞) |
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
КВАДРАТНІ РІВНЯННЯ
Завдання з вибором однієї правильної відповіді
Обчисліть суму коренів рівняння 𝑥2 + 3𝑥 − 4 = 0. № 4, 2021д
|
А |
Б |
В |
Г |
|
−4 |
−3 |
3 |
4 |
Розв’яжіть рівняння 𝑥2 = 25𝑥. № 7, 2020д
|
А |
Б |
В |
Г |
Д |
|
−5;5 |
0;25 |
25 |
−5;0;5 |
−25;0 |
Розв’яжіть рівняння 𝑥2 − 4𝑥 + 3 = 0 № 7, 2020
|
А |
Б |
В |
Г |
Д |
|
−4;3 |
1;3 |
−3;−1 |
−2;3 |
−1;4 |
Розв’яжіть рівняння 𝑥2 − 10 = 5𝑥 + 14 № 2, 2017д
|
А |
Б |
В |
Г |
Д |
|
–8; 3 |
–4; –1 |
–3; 8 |
1; 4 |
0; 5 |
Розв’яжіть рівняння 4𝑥2 = 1. № 3, 2016д
|
А |
Б |
В |
Г |
Д |
|
–2; 2 |
2 |
0,25 |
0,5 |
–0,5; 0,5 |
Розв'яжіть рівняння 2𝑥(𝑥 + 2) = 5(𝑥 + 2) № 7, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
–2,5; 2 |
–2 |
2,5 |
–2; 0,4 |
–2; 2,5 |
Завдання відкритої форми з короткою відповіддю
Розв’яжіть рівняння 𝑥4 − 𝑥2 − 20 = 0. У відповідь запишіть добуток усій його дійсних коренів. № 28, 2021
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
РІВНЯННЯ З МОДУЛЕМ
Завдання з вибором однієї правильної відповіді
Розв'яжіть рівняння ![]() . № 17, 2015_ІІ
. № 17, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
|
|
–12; 12 |
|
Розв'яжіть рівняння ![]() № 16, 2015_І
№ 16, 2015_І
|
А |
Б |
В |
Г |
Д |
|
–5; 5 |
–20; 20 |
20 |
5 |
–0,2; 0,2 |
Укажіть корінь рівняння |𝑥2 − 6𝑥| = 9, який належить проміжку (–2;1]. № 15, 2008
|
А |
Б |
В |
Г |
Д |
|
3 − 3√2 |
3 − √2 |
1 |
2 |
4 − 2√2 |
Укажіть, скільки дійсних коренів має рівняння 𝑥3 − 4|𝑥| = 0 № 14, 2007
|
А |
Б |
В |
Г |
Д |
|
жодного |
один |
два |
три |
більше трьох |
Завдання відкритої форми з короткою відповіддю
Розв’яжіть рівняння ||2𝑥 − 1| − 3| = 5. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше одного кореня, то у відповідь запишіть добуток усіх коренів. № 34, 2010_І
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ІРАЦІОНАЛЬНІ РІВНЯННЯ
Завдання з вибором однієї правильної відповіді
![]()
Укажіть проміжок, якому належить корінь рівняння √𝑥 + 12 = 3 № 10, 2021
|
А |
Б |
В |
Г |
Д |
|
[−12; −6) |
[−6; 0) |
[0; 6) |
[6; 12) |
[12; +∞) |
![]()
Розв’яжіть рівняння 4√𝑥 = 1. № 7, 2018
|
А |
Б |
В |
Г |
Д |
|
|
|
16 |
|
|
Укажіть проміжок, якому належить корінь рівняння ![]() № 9, 2017
№ 9, 2017
|
А |
Б |
В |
Г |
Д |
|
[−3; −1) |
[−1; 0) |
[0; 1) |
[1; 3) |
[3; 6) |
Якому з наведених проміжків належить корінь рівняння ![]() № 11, 2014
№ 11, 2014
|
А |
Б |
В |
Г |
Д |
|
(−30; −20) |
(−20; −10) |
(−10; 0) |
(0; 10) |
(10; 20) |
Укажіть проміжок, якому належить корінь рівняння ![]() № 12, 2013_І
№ 12, 2013_І
|
А |
Б |
В |
Г |
Д |
|
(−20; −10) |
(−10; −5) |
(−5; 5) |
(5; 10) |
(10; 20) |
Завдання відкритої форми з короткою відповіддю
Розв’яжіть рівняння ![]() . Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше, ніж один корінь, то у відповідь запишіть суму всіх коренів. № 36, 2010_ІІ
. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше, ніж один корінь, то у відповідь запишіть суму всіх коренів. № 36, 2010_ІІ
![]()
Розв’яжіть рівняння 𝑥 − 5 + √2𝑥2 − 14𝑥 + 13 = 0. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток. № 28, 2008
![]()
Розв’яжіть рівняння (𝑥2 − 9)√−15 + 8𝑥 − 𝑥2 = 0. У відповідь запишіть суму коренів.
№ 26, 2007
Розв’яжіть рівняння ![]() . Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має кілька коренів, запишіть у відповідь їх добуток.
. Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має кілька коренів, запишіть у відповідь їх добуток.
№ 26, 2006
Розв’яжіть рівняння ![]() № 18, 2005
№ 18, 2005
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ПОКАЗНИКОВІ РІВНЯННЯ
Завдання з вибором однієї правильної відповіді
![]()
Якому з наведених проміжків належить корінь рівняння 2𝑥+3 − 3 ∙ 2𝑥 = 10√2?
№ 20, 2019
|
А |
Б |
В |
Г |
Д |
|
(−∞; 0) |
[0; 0,5) |
[0,5; 1) |
[1; 2) |
[2; +∞) |
Розв’яжіть рівняння 22𝑥 = 2![]() 13 № 3, 2017
13 № 3, 2017
|
А |
Б |
В |
Г |
Д |
|
–3 |
–2 |
–1,5 |
1,5 |
2 |
Розв'яжіть рівняння 4𝑥 = 8 № 7, 2015_І
|
А |
Б |
В |
Г |
Д |
|
|
|
|
2 |
32 |
Якому з наведених проміжків належить корінь рівняння ![]() ? № 14, 2014д
? № 14, 2014д
|
А |
Б |
В |
Г |
Д |
|
(–∞; –5] |
(–5; –2] |
(–2; 0] |
(0; 2] |
(2; +∞) |
𝑥+3 = ( 1 )𝑥 №16, 2011
Якому з наведених нижче проміжків належить корінь рівняння 5
125
|
А |
Б |
В |
Г |
Д |
|
(–3; –2] |
(–2; –1] |
(–1; 0] |
(0; 1] |
(1;3] |
Якому з наведених нижче проміжків належить корінь рівняння 2𝑥 = 1 №7, 2010_І 8
|
А |
Б |
В |
Г |
Д |
|
(–6; –4] |
(–4; –2] |
(–2; 0] |
(0; 2] |
(2; 4] |
![]() Розв’яжіть рівняння 3𝑥 = 2√3 №16, 2008
Розв’яжіть рівняння 3𝑥 = 2√3 №16, 2008
6
|
А |
Б |
В |
Г |
Д |
|
рівняння не має коренів |
–1 |
–0,5 |
0,5 |
1 |
![]() Розв’яжіть рівняння 3√8𝑥 = √2 ∙ 3√2 № 13, 2007
Розв’яжіть рівняння 3√8𝑥 = √2 ∙ 3√2 № 13, 2007
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Завдання відкритої форми з короткою відповіддю
Розв'яжіть рівняння 3𝑥 ∙ 4𝑥 = (12𝑥+1)5 № 26, 2013_ІІ
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ЛОГАРИФМІЧНІ РІВНЯННЯ
Завдання з вибором однієї правильної відповіді
Укажіть проміжок, якому належить корінь рівняння log1![]() (𝑥 + 1) = −2. № 17,2020д
(𝑥 + 1) = −2. № 17,2020д
3
|
А |
Б |
В |
Г |
Д |
|
(−11; −2] |
(−2; 1] |
(1; 4] |
(4; 7] |
(7; 9] |
1
Укажіть проміжок, якому належить корінь рівняння log64 𝑥 = 2![]() . № 16,2020
. № 16,2020
|
А |
Б |
В |
Г |
Д |
|
(−∞; 0] |
(0; 1] |
(1; 6] |
(6; 32) |
[32; +∞) |
Укажіть число, що є коренем рівняння − log2 𝑥 = 3. № 7, 2018д
|
А |
Б |
В |
Г |
Д |
|
−9 |
−8 |
−6 |
|
|
Яке з наведених чисел є коренем рівняння log4(𝑥 − 1) = 3. № 5, 2018
|
А |
Б |
В |
Г |
Д |
|
4 |
13 |
63 |
65 |
82 |
Якому проміжку належить корінь рівняння log2 𝑥 = 2 log2 3? № 20, 2017д
|
А |
Б |
В |
Г |
Д |
|
(0; 2] |
(2; 4] |
(4; 6] |
(6; 8] |
(8; 10] |
Якому з наведених проміжків належить корінь рівняння log3 𝑥 = 2? № 16, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
(–4; –1] |
(–1; 2] |
(2; 5] |
(5; 8] |
(8; 11] |
Завдання відкритої форми з короткою відповіддю
Розв’яжіть рівняння log25 𝑥 + log5 𝑥 = 2. Якщо рівняння має один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму. Якщо рівняння не має коренів, запишіть v відповіді число 100. № 30, 2015_І
Розв’яжіть рівняння ![]() . Якщо рівняння має єдиний корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100. № 30, 2015_ІІ
. Якщо рівняння має єдиний корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100. № 30, 2015_ІІ
Розв’яжіть рівняння log0,4(5𝑥2 − 8) = log0,4(−3𝑥). Якщо рівняння має один корінь,
запишіть його у відповіді. Якщо рівняння має кілька коренів, запишіть у відповіді їхню суму. № 29, 2014
Розв’яжіть рівнянняlog6(𝑥 − 3) + log6(𝑥 − 8) = 2. Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму.
№ 25, 2009
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
Розв’яжіть рівняння lg log2 log3 𝑥 = 0 № 13, 2005
|
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
Завдання з вибором однієї правильної відповіді |
1 |
Розв'яжіть рівняння ![]() № 20, 2019д
№ 20, 2019д
А ![]()
|
Б |
(−1)𝑘𝜋 + 3𝜋𝑘, 𝑘 ∈ 𝑍 |
|
В |
±𝜋 + 6𝜋𝑘, 𝑘 ∈ 𝑍 |
Г ![]()
Д ![]()
Розв'яжіть рівняння ![]() № 20, 2016
№ 20, 2016
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
![]()
Розв'яжіть рівняння 𝑡𝑔(3𝑥) = √3 № 12, 2014
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
|
|
|
|
Розв'яжіть рівняння 2 sin 𝑥 = 1 |
№ 17, 2009 |
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Розв'яжіть рівняння ![]() № 11, 2008
№ 11, 2008
А ![]()
Б ![]()
В ![]()
Г ![]()
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
Д ![]()
Розв'яжіть рівняння ![]() № 8, 2006
№ 8, 2006
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
|
|
|
|
Розв’яжіть рівняння ctg(3𝑥) = 6 А arcctg 2 + 𝜋𝑘, 𝑘 ∈ 𝑍 |
№ 6, 2005 |
Б ![]()
В ![]()
Г 2 + 𝜋𝑘, 𝑘 ∈ 𝑍
Д ![]()
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
РІВНЯННЯ (УЗАГАЛЬНЕННЯ)
Завдання з вибором однієї правильної відповіді
Укажіть число, що є коренем рівняння ![]() . № 4, 2020д
. № 4, 2020д
|
А |
Б |
В |
Г |
Д |
|
20 |
|
10 |
80 |
|
Розв'яжіть рівняння (𝑥 + 1)(2𝑥 − 3) = 0. № 3, 2019
|
А |
Б |
В |
Г |
Д |
|
−3; 1 |
−1,5; 1 |
|
−1; 3 |
−1; 1,5 |
![]() Розв'яжіть рівняння 1 = 1 № 6, 2014д
Розв'яжіть рівняння 1 = 1 № 6, 2014д
2𝑥 2−3𝑥
|
А |
Б |
В |
Г |
Д |
|
–2 |
–0,4 |
2,5 |
0,4 |
2 |
Укажіть рівняння, коренем якого є число 2. № 4, 2014
|
А |
Б |
В |
Г |
Д |
|
1
𝑥 − 2 |
𝑥2 + 4 = 0 |
5𝑥 + 12 = 0 |
3𝑥 − 6
𝑥 |
𝑥 + 2 = 𝑥 |
Розв'яжіть рівняння ![]() № 1, 2011
№ 1, 2011
|
А |
Б |
В |
Г |
Д |
|
0,1 |
10 |
2,5 |
0,4 |
–3 |
Задано рівняння: № 10, 2006
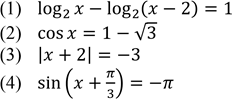
Укажіть рівняння, яке НЕ МАЄ коренів на множині дійсних чисел
|
А |
Б |
В |
Г |
Д |
|
(1) і (4) |
(2) і (3) |
(1) і (2) |
(3) і (4) |
Інша відповідь |
Завдання на встановлення відповідності
Розв'яжіть рівняння (1–4). Установіть відповідність між кожним рівнянням та твердженням (А–Д), що є правильним для цього рівняння. № 22, 2012_ІІ
Рівняння Твердження
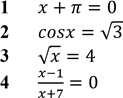 А коренем рівняння є ірраціональне число
А коренем рівняння є ірраціональне число
Б коренем рівняння є число 16
В рівняння не має коренів
Г рівняння має два корені
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
Д корінь рівняння належить відрізку [–2; 2]
Розв'яжіть рівняння (1–4). Установіть відповідність між кожним рівнянням та кількістю його коренів (А–Д) на відрізку [–5; 5]. № 23, 2012_І
Рівняння Кількість коренів на відрізку [–5; 5]
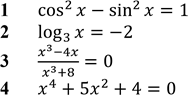 А жодного
А жодного
Б один В два
Г три
Д чотири
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
РІВНЯННЯ З ПАРАМЕТРАМИ
Завдання відкритої форми з розгорнутою відповіддю
Задано рівняння ![]() , де 𝑥 – змінна, 𝑎 – стала.
, де 𝑥 – змінна, 𝑎 – стала.
1. Розв’яжіть рівняння 3𝑥+1 + 3𝑥+3 − 10 = 0
2. Розв’яжіть задане рівняння залежно від значень 𝑎. № 35, 2020д
Задано рівняння ![]() – змінна, 𝑎 – стала.
– змінна, 𝑎 – стала.
1. Розв’яжіть рівняння 52𝑥+1 − 25𝑥 − 20 = 0
2. Розв’яжіть задане рівняння залежно від значень 𝑎. № 35, 2020
Розв’яжіть рівняння ![]() залежно від значень параметра а
залежно від значень параметра а
№ 33, 2016д
Розв’яжіть рівняння ![]() залежно від значень параметра а.
залежно від значень параметра а.
№ 33, 2016
При яких значеннях параметра а рівняння ![]() на проміжку [0; 1] має рівно два різних корені.
на проміжку [0; 1] має рівно два різних корені.
А ![]()
Б ![]()
В ![]()
Г ![]()
Д таких значень не існує № 38, 2015_І
При якому найбільшому від'ємному значенні параметра а рівняння ![]() має один корінь? № 33, 2013_ІІ
має один корінь? № 33, 2013_ІІ
Знайдіть значення параметра а, при якому корінь рівняння ![]() належить проміжку
належить проміжку ![]() № 33, 2013_І
№ 33, 2013_І
При якому найменшому значенні параметра а рівняння ![]() має хоча б один корінь?
має хоча б один корінь?
№ 32, 2012_І
При якому найменшому цілому значенні параметра а рівняння ![]() має лише два різні корені?
має лише два різні корені?
№ 32, 2012_І
|
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ Знайдіть найменше значення а, при якому має розв'язки рівняння |
2 |
![]() № 35, 2011
№ 35, 2011
|
Знайдіть найменше ціле значення параметра а, при якому рівняння |
|
|
log8(𝑥 + 2) = log8(2𝑥 − 𝑎) має корені. |
№ 32, 2007
|
Знайдіть всі цілі числа 𝑘, при яких рівняння ![]() має розв'язки.
має розв'язки.
Знайдіть ці розв'язки. № 27, 2005
СИСТЕМИ РІВНЯНЬ
Завдання з вибором однієї правильної відповіді
![]() ,
,
Розв’яжіть систему рівнянь Для одержаного розв’язку(𝑥0; 𝑦0) обчисліть суму 𝑥0 + 𝑦0. № 17, 2019д
|
А |
Б |
В |
Г |
Д |
|
2 |
12 |
3 |
5 |
4 |
Розв’яжіть систему рівнянь ![]() . Для одержаного розв’язку (𝑥0; 𝑦0) укажіть добуток 𝑥0 ∙ 𝑦0. № 16, 2019
. Для одержаного розв’язку (𝑥0; 𝑦0) укажіть добуток 𝑥0 ∙ 𝑦0. № 16, 2019
|
А |
Б |
В |
Г |
Д |
|
5 |
10 |
20 |
40 |
48 |
![]() Розв’яжіть систему рівнянь
Розв’яжіть систему рівнянь
.
Якщо (𝑥0; 𝑦0) – розв’язок цієї системи, то 𝑥0 = № 14, 2018
|
А |
Б |
В |
Г |
Д |
|
–6 |
–16 |
–9 |
2 |
6 |
![]() Розв’яжіть систему рівнянь
Розв’яжіть систему рівнянь
.
Якщо (𝑥0; 𝑦0) – розв’язок цієї системи, то 𝑥0 + 𝑦0 = № 9, 2016д
|
А |
Б |
В |
Г |
Д |
|
–7 |
7 |
–1 |
8 |
–8 |
![]() Розв’яжіть систему рівнянь
Розв’яжіть систему рівнянь
.
Якщо (𝑥0; 𝑦0) – розв’язок цієї системи, то 𝑥0 ∙ 𝑦0 = № 6, 2016
|
А |
Б |
В |
Г |
Д |
|
–36 |
–14 |
–6 |
4 |
6 |
![]() ,
,
Розв'яжіть систему рівнянь
Якщо (𝑥0; 𝑦0) – розв'язок цієї системи, то 𝑥0 + 𝑦0 = № 14, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
–4 |
–3 |
1 |
5 |
15 |
![]() Розв'яжіть систему рівнянь
Розв'яжіть систему рівнянь
.
Для одержаного розв'язку (𝑥0; 𝑦0) системи обчисліть суму 𝑥0 + 𝑦0 № 13, 2015_І
|
А |
Б |
В |
Г |
Д |
|
11 |
21 |
–7 |
–10 |
–14 |
![]() Розв’яжіть систему
Розв’яжіть систему
.
Якщо (𝑥0; 𝑦0) – розв’язок цієї системи, то 𝑥0 = № 8, 2014д
|
А |
Б |
В |
Г |
Д |
|
–24 |
36 |
4,8 |
7,2 |
–36 |
![]() ,
,
Розв'яжіть систему рівнянь
Для одержаного розв'язку (𝑥0; 𝑦0) системи знайдіть суму 𝑥0 + 𝑦0. № 9, 2013_І
|
А |
Б |
В |
Г |
Д |
|
–18 |
3 |
4 |
8 |
12 |
![]() Розв'яжіть систему
Розв'яжіть систему
.
Для одержаного розв'язку (𝑥0; 𝑦0) обчисліть суму 𝑥0 + 𝑦0 № 9, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
–2 |
–1 |
1 |
2 |
–4 |
Завдання відкритої форми з короткою відповіддю
𝑦 + 𝑥 = 3,
Розв'яжіть систему рівнянь {𝑥2 + 4 = 8𝑦.
Якщо пара (𝑥0; 𝑦0) є єдиним розв’язком цієї системи рівнянь, то запишіть у відповідь добуток 𝑥0 ∙ 𝑦0. Якщо пари (𝑥1; 𝑦1) та (𝑥2; 𝑦2) є розв'язками цієї системи рівнянь, то запишіть у відповідь найменший із добутків 𝑥1 ∙ 𝑦1 та 𝑥2 ∙ 𝑦2
№ 27, 2012_ІІ
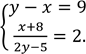 ,
,
Розв'яжіть систему рівнянь
Запишіть у відповідь добуток 𝑥0 ∙ 𝑦0. якщо пара (𝑥0; 𝑦0) є розв’язком цієї системи рівнянь.
№ 27, 2012_І
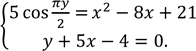 ,
,
Розв'яжіть систему
Якщо система має єдиний розв'язок (𝑥0; 𝑦0), то у відповідь запишіть суму 𝑥0 + 𝑦0, якщо система має більше, ніж один розв'язок, то у відповідь запишіть кількість усіх розв'язків.
№ 36, 2010_І
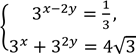 Розв'яжіть систему рівнянь
Розв'яжіть систему рівнянь
.
Для одержаного розв'язку (𝑥0; 𝑦0) системи знайдіть ДОБУТОК 𝑥0 ∙ 𝑦0
№ 29, 2009
Розв’яжіть систему рівнянь 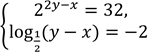 .
.
Запишіть у відповідь добуток 𝑥0 ∙ 𝑦0, якщо пара (𝑥0; 𝑦0) є розв’язком вказаної системи рівнянь.
№ 27, 2007
Розв'яжіть систему рівнянь ![]() ,
,
Запишіть у відповідь СУМУ 𝑥0 + 𝑦0, якщо пара (𝑥0; 𝑦0) є розв'язком вказаної системи рівнянь.
№ 27, 2006
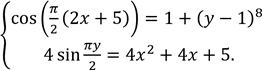 ,
,
Розв'яжіть систему рівнянь
Запишіть у відповідь ДОБУТОК 𝑥0 ∙ 𝑦0, якщо пара (𝑥0; 𝑦0) є розв'язком системи рівнянь.
№ 33, 2006
![]() Знайдіть добуток 𝑥𝑦, якщо пара (𝑥; 𝑦) є розв’язком системи рівнянь
Знайдіть добуток 𝑥𝑦, якщо пара (𝑥; 𝑦) є розв’язком системи рівнянь
.
№ 20, 2005
ТИПИ ЧИСЕЛ. ЗВИЧАЙНІ ДРОБИ. ДЕСЯТКОВІ ДРОБИ
Завдання з вибором однієї правильної відповіді
У під’їзді шістнадцятиповерхового будинку на першому поверсі розташовано 6 квартир, а на кожному з решти поверхів – по 8. На якому поверсі квартира № 31, якщо квартири від № 1 і далі пронумеровано послідовно від першого до останнього поверху?
№ 1, 2021д
|
А |
Б |
В |
Г |
|
3 |
4 |
5 |
6 |
У шкільній їдальні за кожен стіл можна посадити щонайбільше 6 учнів. Яка найменша кількість столів має бути в цій їдальні, щоб розсадити в ній 194 учні? № 3, 2020д
|
А |
Б |
В |
Г |
Д |
|
30 |
31 |
32 |
33 |
34 |
У супермаркеті проходить акція: купуєш три однакові шоколадки «Спокуса» - таку саму четверту супермаркет надає безкоштовно. Ціна кожної такої шоколадки – 35 грн. Покупець має у своєму розпорядженні – 220 грн. Яку максимальну кількість шоколадок «Спокуса» він зможе отримати, взявши участь у акції? № 5, 2019д
|
А |
Б |
В |
Г |
Д |
|
5 |
6 |
7 |
8 |
9 |
Якщо ціна паркету (𝑝) пов'язана із ціною деревини для його виробництва (𝑑) співвідношенням![]() № 4, 2019
№ 4, 2019
|
А |
Б |
В |
Г |
Д |
|
|
5𝑝 − 40 |
|
5𝑝 + 40 |
|
𝑎 2 𝑏
Якщо = , то = № 1, 2018д
𝑏 7 𝑎
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Цукерки, що лежать у коробці, можна порівну поділити між двома або трьома дітьми, але не можна поділити порівну між чотирма дітьми. Якому з наведених значень може дорівнювати кількість цукерок у цій коробці? № 3, 2018д
|
А |
Б |
В |
Г |
Д |
|
36 |
40 |
42 |
48 |
50 |
У буфеті друзі купили кілька однакових тістечок вартістю 10 грн кожне і 5 однакових булочок вартістю 𝑥 грн кожна. Яке з чисел може виражати загальну вартість цієї покупки
(у грн), якщо 𝑥 – ціле число? № 3, 2018
|
А |
Б |
В |
Г |
Д |
|
31 |
32 |
33 |
34 |
35 |
Розташуйте в порядку зростання числа: ![]() № 6, 2017д
№ 6, 2017д
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Число 𝑎 в 5 разів більше за додатне число 𝑏. Тоді 𝑎 = № 1, 2016д
|
А |
Б |
В |
Г |
Д |
|
𝑏 − 5 |
|
𝑏 + 5 |
5𝑏 |
|
|
𝑛 − 1, то 7 − 𝑚 = |
|
|
|
|
|
А |
Б |
В |
Г |
Д |
|
𝑛 − 8 |
6 − 𝑛 |
8 − 𝑛 |
𝑛 − 6 |
6 + 𝑛 |
Якщо 𝑚 =№ 1, 2014
Остача від ділення натурального числа 𝑘 на 5 дорівнює 2. Укажіть остачу від ділення на
5 числа 𝑘 + 21 № 3, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
0 |
1 |
2 |
3 |
4 |
Учитель роздав учням певного класу 72 зошити. Кожен учень отримав однакову кількість зошитів. Якому з поданих нижче чисел може дорівнювати кількість учнів у цьому класі? № 2, 2011
|
А |
Б |
В |
Г |
Д |
|
7 |
9 |
10 |
11 |
14 |
Обчисліть ![]() № 4, 2010_ІІ
№ 4, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
|
,3 |
|
|
|
|
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
5
Обчисліть ![]() ∙ 0 № 2, 2010_І
∙ 0 № 2, 2010_І
9
У Оксани є певна кількість горіхів. Коли вона розклала їх у купки по 5 горіхів, то два горіхи залишилися, а коли розклала їх по 3, то зайвих горіхів не виявилося. Яка кількість горіхів із запропонованих варіантів МОГЛА БУТИ в Оксани? № 5, 2009
|
А |
Б |
В |
Г |
Д |
|
32 |
45 |
57 |
63 |
81 |
|
𝑏 , то b = |
|
|
|
|
|
А |
Б |
В |
Г |
Д |
Якщо 𝑎 ![]() 1 № 9, 2009
1 № 9, 2009
|
𝑐(1 − 𝑎) |
𝑐(𝑎 − 1) |
𝑐
1 − 𝑎 |
1 − 𝑎
𝑐 |
1 − 𝑎𝑐 |
Укажіть правильну нерівність № 10, 2009
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Знайдіть натуральне одноцифрове число N, якщо відомо, що сума 510 + N ділиться на 9 без остачі № 1, 2008
|
А |
Б |
В |
Г |
Д |
|
1 |
3 |
5 |
6 |
9 |
4 3
Визначте кількість усіх дробів зі знаменником 28, які більші за , але менші від
7 4
№ 2, 2008
|
А |
Б |
В |
Г |
Д |
|
шість |
чотири |
три |
два |
один |
Укажіть, скільки можна скласти різних правильних дробів, чисельниками і знаменниками яких є числа 2, 3, 4, 5, 6, 7, 8, 9. № 13, 2008
|
А |
Б |
В |
Г |
Д |
|
28 |
56 |
70 |
112 |
Інша відповідь |
Завдання на встановлення відповідності
Установіть відповідність між твердженням про дріб (1–4) та дробом, для якого це
|
твердження є правильним (А–Д). |
|
№ 22, 2019 |
|
Твердження про дріб |
Дріб |
|
1 є правильним А ![]()
2 належить проміжку (1; 1,5) Б ![]()
3 дорівнює значенню виразу 7log7 1,6 В ![]()
5
4 є сумою чисел ![]() Г
Г ![]()
Д
5
Установіть відповідність між виразом (1–4) та твердженням про його значення (А–Д) при а = 15. № 22, 2017д
Вираз Твердження про значення виразу
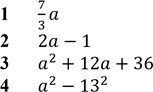 А менше за 20
А менше за 20
Б є простим числом
В є парним
Г ділиться націло на 3
Д ділиться націло на 5
Установіть відповідність між числовим виразом (1–4) та його значенням (А–Д), якщо
![]() № 22, 2016
№ 22, 2016
Вираз Значення виразу
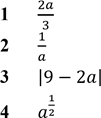 А
А ![]()
Б ![]()
25
В ![]()
Г ![]()
Д ![]()
Установіть відповідність між запитанням (1–4) та правильною відповіддю на нього (А–
Д). № 22, 2015_ІІ
Запитання Відповідь на запитання
|
1 |
Яке число є квадратом натурального числа? |
А |
8 |
|
2 |
Яке число є простим? |
Б |
16 |
|
3 |
Яке число є дільником 8? |
В |
17 |
|
4 |
Яке число кратне 7? |
Г |
27 |
|
|
|
Д |
56 |
Установіть відповідність між твердженням про дріб (1–4) та дробом (А–Д), для якого це
|
твердження є правильним. |
|
№ 22, 2015_І |
|
Твердження про дріб |
Дріб |
|
1 є скоротним А ![]()
2 є неправильним Б ![]()
3 менший за 0,5 В ![]()
4 є оберненим до дробу ![]() Г
Г ![]()
Д ![]()
51
Установіть відповідність між числом (1–4) та множиною, до якої воно належить (А–Д).
№ 26, 2010_ІІ
Число Множина
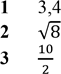 А множина натуральних чисел
А множина натуральних чисел
Б множина складених чисел
В множина цілих чисел, що не є
4 –13 натуральними числами
Г множина дробових чисел
Д множина ірраціональних чисел
Установіть відповідність між числом (1–4) та множиною, до якої воно належить (А–Д).
№ 26, 2010_І
Число Множина
1 –8 А множина парних натуральних чисел
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 5
 Б множина цілих чисел, що не
Б множина цілих чисел, що не
є натуральними числами
В множина раціональних чисел, що не
є цілими числами
Г множина ірраціональних чисел
Д множина простих чисел
НЕРІВНОСТІ. МЕТОД ІНТЕРВАЛІВ
Завдання з вибором однієї правильної відповіді
4𝑥 − 7 ≥ 2𝑥 + 1,
Розв’яжіть систему нерівностей { № 19, 2020д
𝑥 ≥ −3.
|
А |
Б |
В |
Г |
Д |
|
[−1; +∞) |
[−3; 4] |
∅ |
[−3; +∞) |
[4; +∞) |
6 > 2𝑥,
Розв’яжіть систему нерівностей { № 15, 2020
7𝑥 − 28 ≤ 0.
|
А |
Б |
В |
Г |
Д |
|
(−∞; 3) |
(3; 4] |
(−∞; −3) |
(−3; 4] |
(−∞; 4] |
Укажіть число, що є розв'язком нерівності 𝑥2 < 9 № 3, 2019д
|
А |
Б |
В |
Г |
Д |
|
−8 |
−4,5 |
−2 |
3 |
8 |
Яке з наведених чисел є розв'язком нерівності |𝑥| > 3 № 8, 2019
|
А |
Б |
В |
Г |
Д |
|
3 |
1 |
0 |
−3 |
−8 |
Розв’яжіть нерівність |𝑥 + 4| ∙ (𝑥 − 1) < 0 № 20, 2018д
|
А |
Б |
В |
Г |
Д |
|
(−∞; −4) ∪ (1; +∞) |
(−4; 1) |
(−∞; 1) |
(−1; 4) |
(−∞; −4) ∪ (−4; 1) |
Яке з наведених чисел є розв’язком подвійної нерівності 5 ≤ 3𝑥 ≤ 15? №8, 2017д
|
А |
Б |
В |
Г |
Д |
|
5 |
4 |
3 |
2 |
1 |
Розв’яжіть нерівність ![]() . № 13, 2017д
. № 13, 2017д
|
А |
Б |
В |
Г |
Д |
|
(−∞; 2) |
(−∞; −1) ∪ (−1; 2) |
(−1; 2) |
(−∞; −1) ∪ (2; +∞) |
(−∞; −1) |
Розв’яжіть нерівність (𝑥2 + 64)(𝑥 − 5) > 0 № 17, 2017
|
А |
Б |
В |
Г |
Д |
|
(5; +∞) |
(−∞; 5) ∪ (5; +∞) |
(5; 8) |
(−∞; 5) ∪ (8; +∞) |
(−∞; 5) |
𝑥+3
Розв’яжіть нерівність ![]() > 1 № 19, 2016д
> 1 № 19, 2016д
𝑥−2
|
А |
Б |
В |
Г |
Д |
|
(−∞; −2) ∪ (3; +∞) |
(2; +∞) |
(−3; 2) |
(−2; 3) |
(−∞; −3) ∪ (2; +∞) |
Укажіть число, що є розв'язком нерівності![]() № 4, 2016
№ 4, 2016
|
А |
Б |
В |
Г |
Д |
|
–2 |
0 |
2 |
4 |
9 |
Розв'яжіть нерівність (𝑥 + 4)(𝑥 − 8) > 3(𝑥 − 8) № 18, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
(−∞; −1) ∪ (8; +∞) |
(−1; 8) |
(−1; 8) ∪ (8; +∞) |
(−1; +∞) |
(8; +∞) |
Розв'яжіть нерівність 0,2х – 54 < 0. № 3, 2015_І
|
А |
Б |
В |
Г |
Д |
|
(–∞; 27) |
(270; +∞) |
(–∞; 2,7) |
(–∞; 270) |
(10,8; +∞) |
Розв'яжіть нерівність ![]() № 20, 2015_І
№ 20, 2015_І
|
А |
Б |
В |
Г |
Д |
|
{−2} ∪ (3; 6] |
(−∞; – 2] ∪ (3; 6] |
[– 2; 6] |
(−∞; 6] |
(−∞; 3) ∪ (3; 6] |
Розв'яжіть нерівність 𝑥3 ≥ 𝑥2 № 18, 2014д
|
А |
Б |
В |
Г |
Д |
|
(−∞; 0] ∪ [1; +∞) |
[0; 1] |
[1; +∞) |
{0} ∪ [1; +∞) |
[−1; +∞) |
Розв'яжіть нерівність (𝑥 + 4)2 ≤ 16. № 17, 2014
|
А |
Б |
В |
Г |
Д |
|
(–∞; 8] |
(–∞; 0] |
(–∞; 4] |
[–8; 8] |
[–8; 0] |
Розв'яжіть нерівність ![]() 1 < 0 № 8, 2013_ІІ
1 < 0 № 8, 2013_ІІ
𝑥−5
|
А |
Б |
В |
Г |
Д |
|
(–∞; 5) |
(–∞; –5) |
(–∞; 5)∪(5; +∞) |
(–5; +∞) |
(5; +∞) |
Розв'яжіть нерівність ![]() № 17, 2012_ІІ
№ 17, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
(7; +∞) |
(−1; 7) |
(−1; 7) ∪ (7; +∞) |
(−1; +∞) |
(−∞; −1) ∪ (7; +∞) |
Розв'яжіть нерівність ![]() № 14, 2011
№ 14, 2011
|
А |
Б |
В |
Г |
Д |
|
|
(−∞; −1) |
|
|
|
Розв'яжіть нерівність 10 − 3𝑥 > 4 № 1, 2010_І
|
А |
Б |
В |
Г |
Д |
|
(−∞; 2) |
(2; +∞) |
(−3; +∞) |
(−∞; −2) |
(−∞; 2) |
𝑥2+64
Розв’яжіть нерівність ![]() > 0 № 4, 2008
> 0 № 4, 2008
𝑥−5
|
А |
Б |
В |
Г |
Д |
|
(−∞; 5) ∪ (8; +∞) |
(−∞; 5) ∪ (5; +∞) |
(5; 8) |
(5; +∞) |
(−∞; 5) |
Розв’яжіть нерівність ![]() № 4, 2007
№ 4, 2007
|
А |
Б |
В |
Г |
Д |
|
(−2; −3) |
(−2; +∞) |
(−∞; −2) ∪ (−2; +∞) |
(−∞; 3) ∪ (3; +∞) |
(−2; 3) ∪ (3; +∞) |
Розв'яжіть нерівність 𝑎2 > 𝑎 № 4, 2006
|
А |
Б |
В |
Г |
Д |
|
(1; +∞) |
(0; 1) |
(–∞; 0) |
(−∞; 0) ∪ (1; +∞) |
(–∞; 1) |
𝑥−1
Розв’яжіть нерівність ![]() ≤ 0 № 2, 2005
≤ 0 № 2, 2005
𝑥+3
|
А |
Б |
В |
Г |
Д |
|
(−3; 1] |
(−∞; −3) |
(−∞; −3) ∪ [1; +∞) |
[−3; 1] |
(−∞; −3) ∪ (−3; 1) |
Завдання відкритої форми з короткою відповіддю
Розв’яжіть нерівність |𝑥 − 9| ≤ 3. У відповідь запишіть суму всіх її цілих розв’язків на проміжку [−15; 15] № 28, 2021д
Знайдіть КІЛЬКІСТЬ усіх цілих розв'язків нерівності ![]() . Якщо нерівність має
. Якщо нерівність має
безліч цілих розв'язків, то у відповідь запишіть число 100 № 27, 2009
Розв'яжіть нерівність ![]() . У відповіді запишіть суму всіх цілих її розв'язків
. У відповіді запишіть суму всіх цілих її розв'язків
№ 27, 2013_І
Укажіть найменше ціле число, яке є розв’язком нерівності ![]()
№ 23, 2007
Укажіть найменше ціле число, яке є розв'язком нерівності ![]() № 21, 2006
№ 21, 2006
Розв'яжіть нерівність ![]() . У відповідь запишіть найменший цілий розв'язок нерівності № 33, 2009
. У відповідь запишіть найменший цілий розв'язок нерівності № 33, 2009
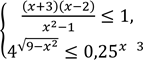 Розв'яжіть систему нерівностей У відповідь запишіть кількість цілих − .
Розв'яжіть систему нерівностей У відповідь запишіть кількість цілих − .
розв'язків системи. Якщо система має безліч цілих розв'язків, то у відповідь запишіть число 100. № 35, 2008
Вкажіть найбільше ціле число, яке є розв’язком нерівності ![]() № 16, 2005
№ 16, 2005
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ПОКАЗНИКОВІ НЕРІВНОСТІ
Завдання з вибором однієї правильної відповіді
Розв’яжіть нерівність 3𝑥 < 27 ∙ 3−𝑥 № 15, 2021д
|
А |
Б |
В |
Г |
Д |
|
|
|
(−∞; 3) |
|
|
Розв’яжіть нерівність 24𝑥−5 ≥ 2 № 7, 2019д
|
А |
Б |
В |
Г |
Д |
|
[1,5; +∞) |
[1,25; +∞) |
[−1; +∞) |
(– ∞; −1] |
|
Розв’яжіть нерівність 2𝑥 + 2𝑥+3 ≥ 144 № 18, 2018
|
А |
Б |
В |
Г |
Д |
|
[34,5; +∞) |
[4; +∞) |
(–∞; 4] |
(–∞; 4,5] |
[4,5; +∞) |
3 𝑥−5 3
Розв’яжіть нерівність ( ) > № 15, 2016д
7 7
|
А |
Б |
В |
Г |
Д |
|
(–∞; 5) |
(–∞; 6) |
(0; 5) |
(5; +∞) |
(6; +∞) |
Розв'яжіть нерівність ![]() . № 5, 2015_ІІ
. № 5, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
(−2; +∞) |
|
(−∞; −2) |
|
|
Розв'яжіть нерівність 2𝑥 ≤ 3 № 16, 2013_І
|
А |
Б |
В |
Г |
Д |
|
(−∞; log2 3] |
(0; log2 3] |
|
(−∞; log3 2] |
[log2 3; +∞) |
![]() 3
3
Розв'яжіть нерівність № 17, 2012_І
|
А |
Б |
В |
Г |
Д |
|
(−3; +∞) |
(3; +∞) |
(−∞; 3) |
(−∞; −3) |
|
1 𝑥 1
Розв’яжіть нерівність ( ) ≤ ![]() № 6, 2009 5 25
№ 6, 2009 5 25
|
А |
Б |
В |
Г |
Д |
|
(–∞; 5] |
(–∞; 2] |
(0; 2] |
[2; +∞) |
[5; +∞) |
Завдання відкритої форми з короткою відповіддю
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2 Розв'яжіть нерівність ![]() . У відповіді запишіть суму всіх цілих розв’язків нерівності на проміжку [–3; 7]. № 30, 2014
. У відповіді запишіть суму всіх цілих розв’язків нерівності на проміжку [–3; 7]. № 30, 2014
Розв'яжіть нерівність ![]() . У відповідь запишіть суму всіх цілих розв'язків цієї нерівності. Якщо нерівність має безліч цілих розв'язків, то у відповідь запишіть число
. У відповідь запишіть суму всіх цілих розв'язків цієї нерівності. Якщо нерівність має безліч цілих розв'язків, то у відповідь запишіть число
100. № 31, 2010_ІІ
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ЛОГАРИФМІЧНІ НЕРІВНОСТІ
Завдання з вибором однієї правильної відповіді
Розв'яжіть нерівність log0,9(3𝑥) > 2 № 13, 2021
|
А |
Б |
В |
Г |
Д |
|
(−∞; 0,27) |
(−∞; 0,6) |
(0,27; +∞) |
(0,6; +∞) |
(0; 0,27) |
Розв'яжіть нерівність log3 𝑥 < −1 № 18, 2016
|
А |
Б |
В |
Г |
Д |
|
|
|
|
(−∞; −3) |
|
Розв'яжіть нерівність log0,4 𝑥 ≥ log0,4 2 № 19, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
(−∞; 2] |
(0,4; 2] |
(0; +∞) |
[2; +∞) |
(0; 2] |
Розв'яжіть нерівність log0,5(𝑥 − 1) > 2 № 23, 2011
|
А |
Б |
В |
Г |
Д |
|
(1; 1,25) |
(2; +∞) |
(1,25; +∞) |
(0; 0,25) |
(–∞;1,25) |
Розв’яжіть нерівність log0,5 5 < log0,5 𝑥 № 14, 2008
|
А |
Б |
В |
Г |
Д |
|
(−5; 0) |
(0; 5) |
(5; +∞) |
(0,5; 5) |
(−∞; 5) |
Розв'яжіть нерівність log0,1 10 < log0,1 𝑥 № 12, 2007
|
А |
Б |
В |
Г |
Д |
|
(10; +∞) |
(0; 10) |
(0,1; 10) |
(–10; 0) |
(–∞; 10) |
Розв'яжіть нерівність log1![]() 3 ∙ log4 𝑥 > 0 № 13, 2006
3 ∙ log4 𝑥 > 0 № 13, 2006
4
|
А |
Б |
В |
Г |
Д |
|
(1; +∞) |
(0; 4) |
(0; 1) |
(4; +∞) |
(–∞; 1) |
Завдання відкритої форми з короткою відповіддю
Розв'яжіть нерівність 𝑥2 + 2log2(−2𝑥) − 15 < 0. У відповіді запишіть суму всіх цілих
|
розв'язків цієї нерівності.
|
№ 30, 2014д |
Знайдіть кількість усіх цілих розв'язків нерівності ![]() . Якщо нерівність має безліч цілих розв'язків, то у відповідь запишіть число 100. № 31, 2010_І
. Якщо нерівність має безліч цілих розв'язків, то у відповідь запишіть число 100. № 31, 2010_І
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ГРАФІЧНЕ РОЗВ’ЯЗАННЯ РІВНЯНЬ І НЕРІВНОСТЕЙ
Завдання з вибором однієї правильної відповіді
Розв’яжіть нерівність log2 𝑥 < 𝑏, використавши рисунок. № 15, 2017
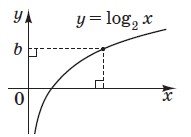
|
А |
Б |
В |
Г |
Д |
|
(0; 2𝑏) |
(0; b) |
(−∞; 2𝑏) |
(log2 𝑏 ; +∞) |
(−∞; 𝑏) |
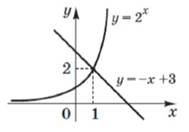
Використовуючи зображені на рисунку графіки функцій, розв'яжіть нерівність
2𝑥 > −𝑥 + 3 № 5, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
(−∞; 2) |
(1; +∞) |
(0; 1) |
(−∞; 1) |
(2; +∞) |
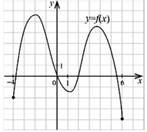
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), яка визначена на відрізку [– 4; 6].
Скільки всього коренів має рівняння 𝑓(𝑥) = 𝑥 на цьому відрізку? № 22, 2010_І
|
А |
Б |
В |
Г |
Д |
|
жодного |
один |
два |
три |
чотири |
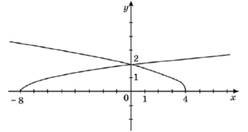
На рисунку зображено графіки функцій ![]() . Укажіть проміжок, на якому виконується нерівність 𝑓(𝑥) ≤ 𝑔(𝑥) № 18, 2008
. Укажіть проміжок, на якому виконується нерівність 𝑓(𝑥) ≤ 𝑔(𝑥) № 18, 2008
|
А |
Б |
В |
Г |
Д |
|
(−∞; 0] |
[−8; +∞) |
[0; +∞) |
[0; 4] |
[– 8; 0] |
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
Завдання відкритої форми з короткою відповіддю
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), що визначена на проміжку (−∞; +∞) і має лише три нулі.
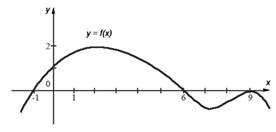
Розв'яжіть систему
![]() .
.
У відповіді запишіть суму всіх цілих розв'язків системи. № 34, 2011
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
СИСТЕМИ РІВНЯНЬ ТА НЕРІВНОСТІ З ПАРАМЕТРАМИ
Завдання відкритої форми з короткою відповіддю
Знайдіть найбільше значення параметра 𝑎, при якому система рівнянь
![]()
має безліч розв'язок. № 34, 2014д
Знайдіть усі від'ємні значення параметра 𝑎, при яких система рівнянь
![]() ,
,
має один розв'язок. Якщо таке значення одне, то запишіть його у відповіді. Якщо таких значень кілька, то у відповіді запишіть їх суму.
№ 34, 2014
Використовуючи графік рівняння |𝑦|=1−|𝑥−12| (див. рисунок), знайдіть усі значення параметра 𝑎, при яких система
![]() | ,
| ,
має єдиний розв’язок. У відповідь запишіть їх суму. № 31, 2008

Знайдіть найбільше ціле значення параметра 𝑎, при якому система рівнянь
𝑦−𝑥=𝑎,
{𝑥2 +𝑦2 =1
|
має два розв'язки.
Знайдіть НАЙМЕНШЕ значення параметра 𝑎, при якому система |
№ 30, 2007 |
![]()
|
має єдиний розв'язок.
Завдання відкритої форми з розгорнутою відповіддю Задано систему рівнянь 𝑎𝑥2 +3𝑎𝑥+32+𝑦2 =27, { 2 𝑥+31+𝑦 =8 де 𝑥,𝑦 – змінні, 𝑎 – довільна стала. 1. Розв’яжіть систему, якщо 𝑎=0 |
№ 31, 2006 |
|
2. Визначте всі розв’язки заданої системи залежно від значень 𝑎. |
№ 34, 2021д |
|
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ Задано систему рівнянь |
2 |
![]() ,
,
де ![]() – змінні,
– змінні, ![]() – довільна стала.
– довільна стала.
1. Розв’яжіть систему, якщо ![]()
2. Визначте всі розв’язки заданої системи залежно від значень ![]() . № 34, 2021 Задано систему нерівностей
. № 34, 2021 Задано систему нерівностей
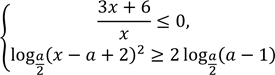
де ![]() – зміна,
– зміна, ![]() – додатна стала.
– додатна стала.
1. Розв’яжіть першу нерівність цієї системи.
2. Визначте множину розв’язків другої нерівності системи залежно від значень ![]() .
.
3. Визначте всі розв’язки системи залежно від значень ![]() . № 33, 2019д
. № 33, 2019д
Задано систему нерівностей
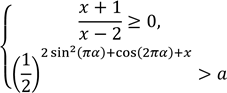
де ![]() – зміна,
– зміна, ![]() – стала.
– стала.
1. Розв’яжіть першу нерівність цієї системи.
2. Визначте множину розв’язків другої нерівності системи залежно від значень ![]() .
.
3. Визначте всі розв’язки системи залежно від значень ![]() . № 33, 2019
. № 33, 2019
Розв’яжіть нерівність
![]()
залежно від значень параметра ![]() .
.
№ 33, 2018д
Розв’яжіть нерівність
![]()
залежно від значень параметра ![]() № 33, 2018
№ 33, 2018
Розв’яжіть систему рівнянь
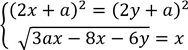 ,
,
залежно від значень параметра ![]() .
.
№ 33, 2017д
Розв’яжіть систему рівнянь
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 3
![]()
залежно від значень параметра 𝑎. № 33, 2017
ТЕКСТОВІ ЗАДАЧІ
Завдання з вибором однієї правильної відповіді
Із заглибленням у надра Землі температура порід підвищується в середньому на 30 С щокожні 100 м. Прилад на першому рівні ствола шахти показує температуру породи +120 С. За якою формулою можна визначити температуру 𝑡 (у 0 С) породи на глибині, що
|
на ℎ м нижче від першого рівня? |
|
|
№ 9, 2021д |
|
|
А |
Б |
В |
Г |
Д |
|
|
|
100ℎ 𝑡 = 3 + 12 |
|
100ℎ 𝑡 = 12 + 3 |
Для місцевості, що лежить на рівні моря, нормальний атмосферний тиск становить 760 мм рт. ст. Із підняттям на кожні 100 м угору атмосферний тиск знижується на 10 мм рт. ст. Укажіть з поміж наведених формулу, за якою визначають атмосферний тиск
|
𝑝 (у мм рт. ст.) на висоті ℎ метрів над рівнем моря. |
|
№ 8, 2021 |
||
|
А |
Б |
В |
Г |
Д |
|
760 ∙ 100 𝑝 = 10ℎ |
100ℎ 𝑝 = 760 − 10 |
|
100ℎ 𝑝 = 760 + 10 |
|
Порожній басейн, що вміщує х м3 води, повністю заповнюють водою за 5 годин (швидкість заповнення є сталою). За якою формулою можна обчислити кількість води V (у м3) у басейні через 2 години після початку його заповнення, якщо басейн був порожній і швидкість заповнення не змінювалась? № 13, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
𝑉 = 2 ∙ 5𝑥 |
|
|
|
З міст А і В, відстань між якими по шосе становить 340 км, одночасно назустріч один одному виїхали автобус і маршрутне таксі зі сталими швидкостями 65 км/год і 80 км/год відповідно. Автобус і маршрутне таксі рухаються без зупинок і ще не зустрілися. За якою формулою можна обчислити відстань S (у км) між автобусом і маршрутним таксі по шосе через t годин після початку руху? № 14, 2012_І
|
А |
Б |
В |
Г |
Д |
|
𝑆 = 340 − 15𝑡 |
𝑆 = 340 + 145𝑡 |
𝑆 = 15𝑡 − 340 |
𝑆 = 145𝑡 − 340 |
𝑆 = 340 − 145𝑡 |
Завдання на встановлення відповідності
З пунктів А і В одночасно по шосе назустріч один одному виїхали два велосипедисти. Вони їхали без зупинок зі сталими швидкостями: перший – зі швидкістю 𝑥км/год, другий – зі швидкістю 𝑦км/год (𝑥 > 𝑦). Через 𝑡 годин (𝑡 > 1) вони зустрілися в точці С і, не зупиняючись, продовжили рух без зміни напрямків. До кожного запитання (1–4)
|
доберіть правильну відповідь (А–Д). |
№ 21, 2013_ІІ |
|
Запитання |
Відповідь |
|
1 На скільки кілометрів зменшилася відстань по шосе |
А (𝑥 + 𝑦)𝑡 |
|
між велосипедистами через 1 годину після початку руху? |
Б (𝑥 − 𝑦)𝑡 |
2 Чому дорівнює відстань по шосе між пунктами В ![]()
А і В (км/год)? Г ![]()
3 На скільки кілометрів більше проїхав перший велосипедист Д 𝑥 + 𝑦 ніж другий, за час від початку руху до моменту зустрічі? 4 За скільки годин перший велосипедист подолає відстань по шосе від точки С до пункту В?
Дві однакові автоматичні лінії виготовляють 16 т шоколадної глазурі за 4 дні. Установіть відповідність між запитанням (1–4) та правильною відповіддю на нього (А–Д). Уважайте, що кожна лінія виготовляє однакову кількість глазурі щодня. № 23, 2013_І
Запитання Відповідь на запитання
1 Скільки тонн шоколадної глазурі дві лінії А 2
виготовляють за 3 дні? Б 4
2 За скільки днів одна лінія виготовить 16 т В 6 шоколадної глазурі? Г 8
3 Скільки тонн шоколадної глазурі виготовить Д 12 одна лінія за 2 дні?
4 Скільки таких ліній потрібно для виготовлення
48 т шоколадної глазурі за 4 дні?
Завдання відкритої форми з короткою відповіддю
Протягом 40 хвилин уроку учні виступили з трьома доповідями однакової тривалості й показали дві презентації. Показ кожної презентації тривав на 10 хвилин більше, ніж доповідь. Визначте тривалість однієї доповіді (у хв). Тривалістю пауз між доповідями й презентаціями знехтуйте. № 26, 2021д
У кінотеатрі квиток на вечірній сеанс на 15 грн дорожчий за квиток на ранковий сеанс. Вартість чотирьох квитків на ранковий сеанс на 220 грн менша за вартість шістьох квитків на вечірній сеанс. Скільки гривень коштує один квиток на ранковий сеанс? Уважайте, що на кожному із сеансів квитки на всі місця коштують однаково.
№ 28, 2020д
Човен проплив 18 км проти течії річки, витративши вдвічі менше часу, ніж на подолання
48 км за течією. Власна швидкість човна є сталою. Визначте власну швидкість човна (у км/год), якщо швидкість течії становить 2,5 км/год. № 28, 2020
Шлях від пристані А до пристані В теплохід, що рухається за течією річки долає за 2 години. На зворотний шлях він витрачає на 15 хвилин більше. Швидкість течії річки дорівнює 2 км/год, власна швидкість теплохода є сталою. Визначте власну швидкість теплохода (у км/год). № 28, 2019д
Маршрутний автобус, рухаючись зі сталою швидкістю, подолав відстань від міста А до міста B за 5 год, а на зворотній шлях витратив на 30 хв менше. Визначте швидкість (у км/год) автобуса на маршруті від А до В, якщо вона на 8 км/год менша за швидкість на маршруті від В до А. Уважайте, що довжина маршрутів від А до В та від В до А, якими рухався маршрутний автобус, рівні. № 28, 2019 Лідія редагує 80 сторінок рукопису у 8 разів швидше, ніж Максим редагує 480 сторінок. Скільки сторінок відредагує Максим за той самий час, за який Лідія відредагує 320 сторінок? Уважайте, що продуктивність роботи і Лідії, і Максима є сталою.
№ 28, 2018д
У майстерні мали виготовити 240 стільців за n днів, причому щодня планували виробляти однакову кількість стільців. Однак, на прохання замовника, завдання виконали на 2 дні раніше запланованого терміну. Для цього довелося денну норму виготовлення збільшити на 4 стільці. Визначте n. № 28, 2018
Човен проходить 24 км за течією ріки за 5 годин і 12 км проти течії за 3 години. Визначте швидкість течії ріки (у км/год). Уважайте, що власна швидкість човна та швидкість течії незмінні. № 28, 2017д
Автобус вирушив з міста А до міста В, відстань між якими становить 150 км. Через 30 хв. із міста А до міста В тією самою дорогою вирушив автомобіль, швидкість якого в ![]() раза більша за швидкість автобуса. Скільки часу (у год) витратив на дорогу з міста А до міста В автомобіль, якщо він прибув до міста В одночасно з автобусом? Уважайте, що автобус та автомобіль рухалися зі сталими швидкостями. № 28, 2017
раза більша за швидкість автобуса. Скільки часу (у год) витратив на дорогу з міста А до міста В автомобіль, якщо він прибув до міста В одночасно з автобусом? Уважайте, що автобус та автомобіль рухалися зі сталими швидкостями. № 28, 2017
Фабрика виготовляє комплекти пластикових меблів, кожен з яких складається зі стола, дивана та двох крісел. На виготовлення дивана витрачається на 1 кг пластику більше, ніж на виготовлення стола, та на 3 кг більше, ніж на виготовлення одного крісла. Відомо, що на виготовлення 10 крісел витрачається пластику стільки ж, як і на виготовлення 2 столів та 4 диванів разом. Скільки кілограмів пластику витрачається на виготовлення одного комплекту пластикових меблів? № 28, 2016д
У готелі для проживання туристів є одномісні, двомісні та тримісні номери. їх всього 124. Якщо всі номери в готелі заповнені, то одночасно в ньому проживає 270 туристів. Скільки всього в цьому готелі тримісних номерів, якщо кількість одномісних номерів дорівнює кількості двомісних номерів? № 28, 2016
Вартість Р (у грн) поїздки таксі обчислюють за формулою:
![]() ( ) ,
( ) ,
де S – відстань (у км), яку проїхало таксі під час поїздки, Рmin – мінімальна вартість поїздки (у грн), t – час (у хв), протягом якого швидкість таксі не перевищувала 5 км/год. Користуючись формулою, обчисліть вартість поїздки (у грн) таксі, якщо S = 10,5 км, Рmin
= 28 грн, t = 12 хв. № 28, 2014
Петро, Микола та Василь уранці відвідали кафе і кожен із них замовив собі на сніданок бутерброд та гарячий напій. Відомо, що Василь не п’є чорний чай, а Микола замовив собі бутерброд із шинкою. Скориставшись таблицею, визначте, скільки грошей (у грн) буде коштувати Миколі, Василю і Петру разом найдешевше замовлення в цьому кафе.
|
Страви |
Ціна, грн |
|
Бутерброд із сиром |
7.00 |
|
Бутерброд із шинкою |
15.00 |
|
Бутерброд із рибою |
17.00 |
|
Кава з молоком |
13.00 |
|
Кава |
12.00 |
|
Чай чорний |
8.00 |
|
Чай зелений |
9.00 |
№ 25, 2012_ІІ
Батьки разом із двома дітьми: Марійкою (4 роки) та Богданом (7 років) — збираються провести вихідний день у парку атракціонів. Батьки дозволяють кожній дитині відвідати не більше трьох атракціонів і кожний атракціон — лише по одному разу. Відомо, що на атракціони «Електричні машинки» і «Веселі гірки» допускають лише дітей старше 6 років. На «Паровозик» Богдан не піде. Для відвідування будь-якого атракціону необхідно купити квиток для кожної дитини. Скориставшись таблицею, визначте максимальну суму коштів (у грн), що витратять батьки на придбання квитків для дітей.
|
Назва атракціону |
Вартість 1 квитка для 1 дитини, грн |
|
Веселі гірки |
17 |
|
Паровозик |
16 |
|
Електричні машинки |
20 |
|
Карусель |
12 |
|
Батут |
15 |
|
Дитяча рибалка |
8 |
|
Лебеді |
13 |
№ 25, 2012_І
Двоє робітників, працюючи разом, можуть скосити траву на ділянці за 2 години 6 хвилин. Скільки часу (у годинах) витратить на скошування трави на цій ділянці другий робітник, працюючи самостійно, якщо йому потрібно на виконання цього завдання на 4 години більше, ніж першому робітникові? № 32, 2011
Тарас може доїхати на велосипеді від села до станції за 3 год, а пішки дійти за 7 год. Його швидкість пішки на 8 км/год менша, ніж на велосипеді. Знайдіть відстань від села до станції (у км). № 32, 2010_ІІ
У фермерському господарстві «Надія» кожен рік озимою пшеницею засівають 600 га полів. Середня врожайність цієї культури в 2007 році становила 24 центнери з одного гектара. Завдяки сприятливим погодним умовам у 2008 році озимої пшениці було зібрано на 19200 центнерів більше, ніж у 2007. Обчисліть середню врожайність озимої пшениці, вирощеної в господарстві «Надія» в 2008 році (у ц/га). (Середня врожайність сільськогосподарської культури – це відношення маси зібраного врожаю цієї культури до загальної площі полів, на яких вона була вирощена.) № 26, 2009
Маємо два водно-сольових розчини. Концентрація солі у першому розчині становить 0,25, а у другому – 0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 50 кілограмів, концентрація солі в якому – 0,34.
№ 29, 2008
На перегоні, довжина якого дорівнює 240 км, поїзд рухався зі швидкістю на 10 км/год менше, ніж мало бути за розкладом, і запізнився на 48 хв. З якою швидкістю мав рухатися поїзд за розкладом? № 24, 2007
Кішка з кошеням з’їдають куплений господарем корм за 8 днів. Якби кішку годували одну, то їй вистачило б корму на 11 днів. На скільки повних днів вистачило б корму кошеняті? № 17, 2005
АРИФМЕТИЧНА ПРОГРЕСІЯ
Завдання з вибором однієї правильної відповіді
В арифметичній прогресії (𝑎𝑛) перший член 𝑎1 = −21, різниця 𝑑 = 1,5. Скільки всього від’ємних членів має ця прогресія? № 16, 2017д
|
А |
Б |
В |
Г |
Д |
|
13 |
14 |
15 |
16 |
18 |
В арифметичній прогресії (𝑎𝑛): 𝑎1 =– 4, 𝑎5 = 𝑎4 + 3. Визначте десятий член 𝑎10 цієї прогресії № 13, 2017
|
А |
Б |
В |
Г |
Д |
|
–31 |
–27 |
26 |
27 |
23 |
В арифметичній прогресії (𝑎𝑛): 𝑎1 + 𝑎3 = 18, різниця 𝑑 = −4. Визначте перший член 𝑎1 цієї прогресії. № 11, 2016д
|
А |
Б |
В |
Г |
Д |
|
5 |
10 |
13 |
15 |
22 |
Задано арифметичну прогресію (𝑎𝑛), у якій різниця 𝑑 = 0,5, п'ятнадцятий член 𝑎15 = 12.
Визначте перший член прогресії 𝑎1 № 12, 2016.
|
А |
Б |
В |
Г |
Д |
|
4,5 |
5 |
6 |
12,5 |
24 |
Арифметичну прогресію (𝑎𝑛) задано формулою 𝑛-го члена 𝑎𝑛 = 4 − 8𝑛. Знайдіть різницю цієї прогресії. № 8, 2014
|
А |
Б |
В |
Г |
Д |
|
8 |
4 |
–2 |
–4 |
–8 |
В арифметичній прогресії (𝑎𝑛)задано 𝑎1 = 4, 𝑎2 = −1. Укажіть формулу для знаходження ![]() № 7, 2013_І
№ 7, 2013_І
|
|
А |
Б |
В |
Г |
|
Д |
|
𝑎𝑛 |
= −1 + 5𝑛 |
𝑎𝑛 = 7 − 3𝑛 |
𝑎𝑛 = 5 − 𝑛 |
𝑎𝑛 = 1 + 3𝑛 |
𝑎𝑛 |
= 9 − 5𝑛 |
У залі кінотеатру 18 рядів. У першому ряду знаходяться 7 місць, а в кожному наступному ряду на 2 місця більше, ніжу попередньому. Скільки всього місць у цьому залі?
№ 11, 2012_І
|
А |
Б |
В |
Г |
Д |
|
432 |
438 |
369 |
450 |
864 |
Яка з поданих нижче послідовностей є арифметичною прогресією? № 4, 2009
|
А |
Б |
В |
Г |
Д |
|
9; 7; 4; 1 |
–4; –2; 0; 1 |
3; 6; 12; 24 |
1; 3; 6; 10 |
3; 7; 11; 15 |
Завдання відкритої форми з короткою відповіддю
Арифметичну прогресію (𝑎𝑛) задано формулою 𝑛 − го члена 𝑎𝑛 = 5 − 3,6𝑛.
1. Визначте шостий член цієї прогресії.
2. Визначте різницю 𝑎4 − 𝑎2. № 24, 2021д
Арифметичну прогресію (𝑎𝑛) задано формулою 𝑛 − го члена 𝑎𝑛 = 2,6𝑛 − 7.
1. Визначте сьомий член цієї прогресії.
2. Визначте різницю 𝑎4 − 𝑎1. № 24, 2021
Другий член арифметичної прогресії (𝑎𝑛) на 7,2 більший за її шостий член.
1. Визначте різницю 𝑑 цієї прогресії.
2. Визначте перший член 𝑎1 цієї прогресії, якщо 𝑎4 = 0,7. № 27, 2020д
В арифметичній прогресії (𝑎𝑛) відомо, що 𝑎2 − 𝑎5 = 7,8.
1. Визначте різницю 𝑑 цієї прогресії.
2. Визначте перший член 𝑎1 цієї прогресії, якщо її третій член 𝑎3 = −1,8. № 27, 2020
За якого від’ємного значення 𝑥 значення виразів 𝑥2 − 4; 3 − 5𝑥 та 2 − 3𝑥 будуть послідовними членами арифметичної прогресії? № 27, 2019
Третій член арифметичної прогресії вдвічі більший за її перший член. Визначте різницю цієї прогресії, якщо сума перших п’яти її членів дорівнює 190. № 27, 2018д
В інструкції з медичного застосування настою лікарської рослини зазначено, що його рекомендовано приймати щоденно упродовж 20 діб. Протягом першої доби пацієнт має випити 370 мл настою, а кожної наступної доби – на одну й ту саму кількість настою менше, ніж попередньої. Останньої доби прийом має становити 85 мл цього лікарського засобу. Яку кількість настою (у мл) вип'є пацієнт за ці 20 діб, якщо дотримуватиметься інструкції? №29, 2015_ІІ
Плавець під час першого тренування подолав дистанцію у 450 м. Кожного наступного тренування він пропливав на 50 м більше, ніж попереднього, поки не досягнув результату 1000 м за одне тренування. Після цього під час кожного відвідування басейну плавець пропливав 1000 м. Скільки всього кілометрів плавець проплив за перші 10 тижнів тренувань, якщо він тренувався тричі кожного тижня? №29, 2015_І
Робітники отримали замовлення викопати криницю. За перший викопаний у глибину метр криниці їм платять 50 грн, а за кожний наступний – на 20 грн більше, ніж за попередній. Скільки грошей (у грн) сплатять робітникам за викопану криницю завглибшки 12 м? № 30, 2010_ІІ
Одним із мобільних операторів було запроваджено акцію «Довше розмовляєш – менше платиш» з такими умовами: плата за з'єднання відсутня; за першу хвилину розмови абонент сплачує 30 коп., а за кожну наступну хвилину розмови – на 3 коп. менше, ніж за попередню; плата за одинадцяту та всі наступні хвилини розмови не нараховується; умови дійсні для дзвінків абонентам усіх мобільних операторів країни. Скільки за умовами акції коштуватиме абоненту цього мобільного оператора розмова тривалістю 8 хвилин (у грн)? № 30, 2010_І Знайдіть суму перших дванадцяти непарних натуральних чисел № 22, 2007
Обчисліть суму перших 20 членів арифметичної прогресії, якщо її перший член дорівнює
2, а сьомий – 20. № 22, 2006
Сума третього і дев’ятого членів арифметичної прогресії дорівнює 8. Знайдіть суму перших одинадцяти членів цієї прогресії № 19, 2005
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ГЕОМЕТРИЧНА ПРОГРЕСІЯ
Завдання з вибором однієї правильної відповіді
У геометричній прогресії (𝑏𝑛): 𝑏1 = 12![]() , 𝑏2 = 14
, 𝑏2 = 14![]() . Визначте 𝑏4. № 12, 2014д
. Визначте 𝑏4. № 12, 2014д
|
А |
Б |
В |
Г |
Д |
|
|
2 |
4 |
|
|
У геометричній прогресії (𝑏𝑛) задано ![]() . Знайдіть знаменник цієї прогресії.
. Знайдіть знаменник цієї прогресії.
№ 4, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Визначте знаменник геометричної прогресії (𝑏𝑛), якщо 𝑏9 = 24,𝑏6 = − 1![]() 9 № 13, 2011
9 № 13, 2011
|
А |
Б |
В |
Г |
Д |
|
|
|
3 |
6 |
–6 |
Завдання відкритої форми з короткою відповіддю
Укажіть ненульове значення 𝑥, за якого значення виразів 𝑥 − 8, 3𝑥 та 6𝑥 є послідовними членами геометричної прогресії. № 27, 2019д
Знаменник геометричної прогресії дорівнює ![]() , а сума чотирьох перших її членів дорівнює 65. Знайдіть перший член цієї прогресії. № 27, 2018
, а сума чотирьох перших її членів дорівнює 65. Знайдіть перший член цієї прогресії. № 27, 2018
Обчисліть суму членів нескінченно спадної геометричної прогресії, у якої 𝑏𝑛 = 5 ∙ 3−𝑛
№ 27, 2008
ОСНОВНІ ЕЛЕМЕНТАРНІ ФУНКЦІЇ ТА ЇХ ХАРАКТЕРИСТИКИ. ГРАФІКИ
Завдання з вибором однієї правильної відповіді
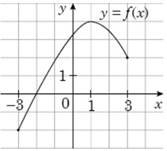
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) визначеної на проміжку [−3; 3]. На якому з наведених проміжків ця функція зростає? № 5, 2020д
|
А |
Б |
В |
Г |
Д |
|
[−3; 3] |
[1; 3] |
[−2; 4] |
[−2; 3] |
[−3; 1] |
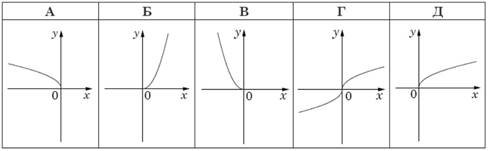
![]()
На одному з наведених рисунків зображено ескіз графіка функції 𝑦 = √𝑥. Укажіть його.
№ 11, 2020д
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) визначеної на проміжку [– 2; 4]. Укажіть нуль цієї функції. № 6, 2020
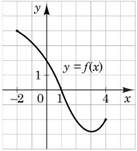
|
А |
Б |
В |
Г |
Д |
|
𝑥 = −2 |
𝑥 = 0 |
𝑥 = 1 |
𝑥 = 2 |
𝑥 = 4 |
На якому з рисунків зображено ескіз графіка функції 𝑦 = (0,5)𝑥? № 10, 2020
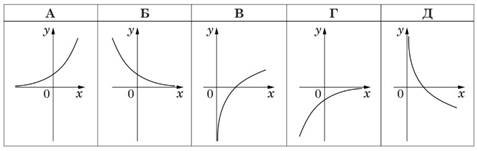
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) визначеної на проміжку [–2;4]. Цей графік перетинає вісь у в одній із зазначених точок. Укажіть цю точку. № 2, 2019д
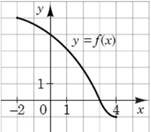
|
А |
Б |
В |
Г |
Д |
|
(4;0) |
(3;4) |
(0;3) |
(3;0) |
(0;4) |
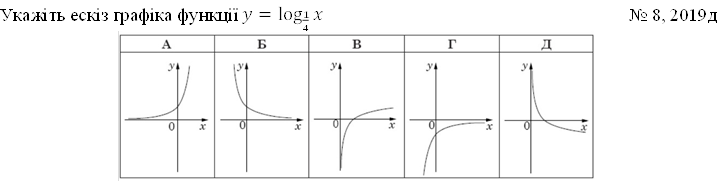
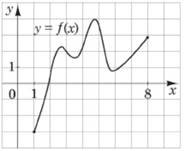
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) визначеної на проміжку [1;8]. Скільки нулів має ця функція на заданому проміжку. № 7, 2019
|
А |
Б |
В |
Г |
Д |
|
жодного |
один |
два |
три |
чотири |
Яку з наведених властивостей має функція ![]() . № 9, 2019
. № 9, 2019
|
А |
набуває лише невід’ємних значень |
|
Б |
спадає по всій області визначення |
|
В |
парна |
|
Г |
періодична |
|
Д
|
має дві точки екстремуму |
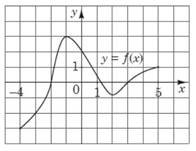
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) визначеної на проміжку [–4;5]. Точка (𝑥0; −2) належить графіку цієї функції. Визначте абсцису 𝑥0 цієї точки. № 4, 2018д
|
А |
Б |
В |
Г |
Д |
|
3 |
2 |
0 |
–2 |
–3 |
Укажіть з поміж наведених функцію 𝑓(𝑥), для кожного 𝑥 з області її визначення виконується рівність 𝑓(−𝑥) = −𝑓(𝑥). № 15, 2018д
|
А |
Б |
В |
Г |
Д |
|
𝑓(𝑥) = 𝑥2 |
𝑓(𝑥) = 3𝑥 |
𝑓(𝑥) = 2𝑥 + 5 |
𝑓(𝑥) = log3 𝑥 |
|
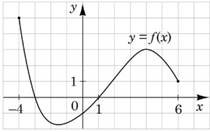
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) визначеної на проміжку [–4; 6]. Укажіть найбільше значення функції 𝑓на цьому проміжку. № 4, 2018
|
А |
Б |
В |
Г |
Д |
|
–4 |
3 |
4 |
5 |
6 |
Знайдіть область визначення функції ![]() № 8, 2018
№ 8, 2018
|
А |
(−∞; 2) ∪ (2; +∞) |
|
Б |
(−∞; – 1) ∪ (2; +∞) |
|
В |
(−∞; – 2) ∪ (– 2; +∞) |
|
Г |
(−∞; – 1) ∪ (– 1; 2) ∪ (2; +∞) |
|
Д |
(−∞; +∞)
|
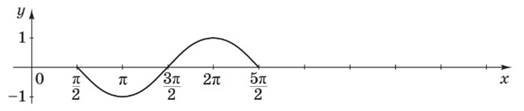
На рисунку зображено фрагмент графіка періодичної функції з періодом 𝑇 = 2𝜋, яка визначена на множині дійсних чисел. Укажіть серед наведених точку, що належить цьому графіку. № 17, 2018
|
А |
Б |
В |
Г |
Д |
|
(1; 2𝜋) |
(3𝜋; 0) |
(−1; 5𝜋) |
(5𝜋; 0) |
(5𝜋; −1) |
Функція 𝑦 = 𝑓(𝑥) визначена і зростає на проміжку [–3; 2]. На рисунку зображено графік цієї функції на проміжку [–3; 0]. Яка з наведених точок може належати графіку цієї функції № 3, 2017д
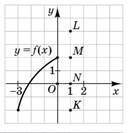
|
А |
Б |
В |
Г |
Д |
|
K |
L |
O |
M |
N |
Визначте точку перетину графіка функції 𝑦 = 2𝑥 − 2 з віссю 𝑥. № 6, 2017
|
А |
Б |
В |
Г |
Д |
|
(0; –2) |
(–2; 0) |
(1; 0) |
(0; 1) |
(1; –2) |
На одному з рисунків зображено ескіз графіка функції ![]() . Укажіть цей рисунок
. Укажіть цей рисунок
№ 4, 2016д
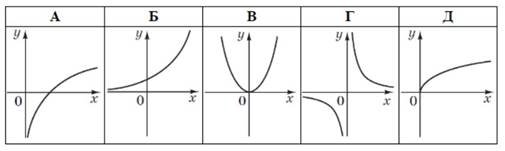
Графіком однієї з наведених функцій є пряма. Укажіть цю функцію. № 3, 2016
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 2𝑥 |
𝑦 = 𝑥2 − 2𝑥 |
𝑦 = cos (2𝑥) |
|
𝑦 = 2𝑥 |
На рисунку зображено ескіз графіка функції 𝑦 = 𝑥2 + 2𝑥 − 3. На якому з проміжків ця функція спадає? № 8, 2015_ІІ
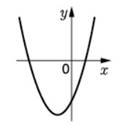
|
А |
Б |
В |
Г |
Д |
|
(–∞; 1] |
(–∞; –1] |
[–1; +∞) |
[–3;–1] |
[1;+∞) |
Укажіть рівняння прямої, що проходить через точку 𝑂(0; 0) № 11, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
𝑦 = −2𝑥 |
𝑦 = 𝑥 + 2 |
𝑦 = 𝑥 − 2 |
𝑦 = 2 − 𝑥 |
𝑦 = −2 |
На рисунку зображено фрагмент графіка однієї з наведених функцій на проміжку ![]()
№ 13, 2015_ІІ
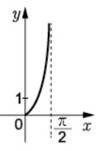
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑐𝑡𝑔𝑥 |
𝑦 = 2𝑥 |
𝑦 = 𝑥2 |
|
𝑦 = 𝑡𝑔𝑥 |
Графік функції, визначеної на проміжку [–5; 4], проходить через одну з наведених точок
(див. рисунок). Укажіть цю точку. № 4, 2015_І
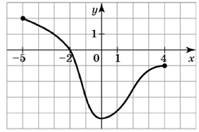
|
А |
Б |
В |
Г |
Д |
|
(–5; –2) |
(1; –3) |
(–1; 4) |
(–3; 1) |
(0; –2) |
Яку властивість із наведених має функція 𝑦 = 2𝑥 – 9? № 15, 2015_І
|
А |
Б |
В |
Г |
Д |
|
є парною |
є непарною |
є періодичною |
є спадною |
є зростаючою |
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), визначеної на відрізку [–7;7].
Користуючись рисунком, знайдіть 𝑓(2). № 1, 2014д
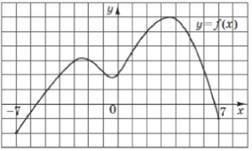
|
А |
Б |
В |
Г |
Д |
|
–4 |
0 |
6 |
2 |
5 |
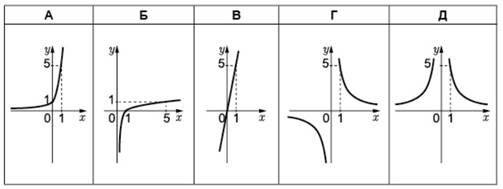
На якому рисунку зображено ескіз графіка функції![]() № 2, 2014
№ 2, 2014
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), визначеної на проміжку [–6; 6]. Яку властивість має функція 𝑦 = 𝑓(𝑥)? № 10, 2014
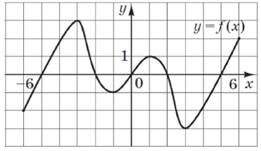
|
А |
Б |
В |
Г |
Д |
|
функція є періодичною |
функція зростає на проміжку [–6; 6] |
функція спадає на проміжку [–6; 6] |
функція є парною |
функція є непарною |
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), визначеної на проміжку [–5; 3]. Укажіть проміжок, на якому функція 𝑦 = 𝑓(𝑥) зростає. № 8, 2013_І
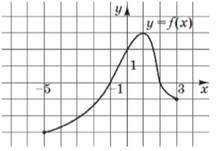
|
А |
Б |
В |
Г |
Д |
|
[0; 3] |
[–1; 2] |
[1; 3] |
[–3; 3] |
[–5;1] |
Укажіть парну функцію № 14, 2013_І
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 4𝑥 |
𝑦 = 𝑥 |
𝑦 = √𝑥 |
𝑦 = 𝑡𝑔𝑥 |
𝑦 = |𝑥| |
Укажіть область визначення функції 𝑦 = log3(𝑥 + 9) № 7, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
(9; +∞) |
(–9; +∞) |
(–9; 0) |
(0; +∞) |
(–∞; +∞) |
Знайдіть область визначення функції ![]() № 2, 2012_І
№ 2, 2012_І
|
А |
Б |
В |
Г |
Д |
|
(−∞; +∞) |
(−∞; 0) ∪ (0; +∞) |
|
|
|
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), визначеної на проміжку [–4; 4]. Знайдіть множину всіх значень 𝑥, для яких 𝑓(𝑥) < − 2. № 5, 2012_І
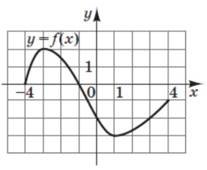
|
А |
Б |
В |
Г |
Д |
|
[0; 3] |
[–3; 2] |
[–1; 4] |
[–3; –2] |
[–4; 0] |
Укажіть лінійну функцію, графік якої паралельний вісі абсцис і проходить через точку
A(–2; 3)? № 4, 2011
|
А |
Б |
В |
Г |
Д |
|
|
𝑦 = −2 |
𝑥 = −2 |
𝑥 = 3 |
𝑦 = 3 |
Функція 𝑦 = 𝑓(𝑥) є спадною на проміжку (−∞; +∞). Укажіть правильну нерівність.
№ 18, 2011
|
А |
Б |
В |
Г |
Д |
|
𝑓(1) > 𝑓(−1) |
𝑓(1) < 𝑓(8) |
𝑓(1) > 𝑓(0) |
𝑓(−1) < 𝑓(0) |
𝑓(1) > 𝑓(10) |
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), яка визначена на відрізку [–4; 6].
Укажіть усі значення 𝑥, для яких виконується нерівність 𝑓(𝑥) ≥ 2? № 23, 2010_ІІ
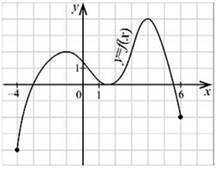
|
А |
Б |
В |
Г |
Д |
|
{2} ∪ [3; 5] |
[−4; 3] ∪ [5; 6] |
[3; 5] |
[2; 4] |
{−1} ∪ [3; 5] |
У прямокутній системі координат зображено точку, що є вершиною параболи 𝑦 = 𝑥2 + 𝑏𝑥 + 𝑐 (див. рисунок). Укажіть правильне твердження щодо коефіцієнтів 𝑏 і 𝑐.
№ 25, 2010_ІІ
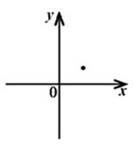
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
На одному з рисунків зображено ескіз графіка функції 𝑦 = 3𝑥. Укажіть цей рисунок.
№ 20, 2010_І
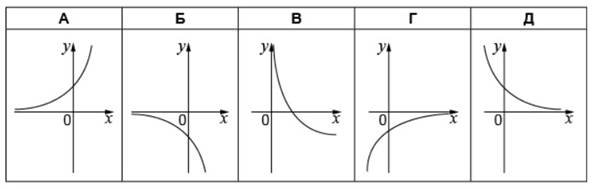
На рисунку зображено ескіз графіка функції 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐. Укажіть правильне твердження щодо коефіцієнтів 𝑎, 𝑏 і 𝑐. № 25, 2010_І
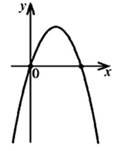
|
А |
Б |
В |
Г |
Д |
|
𝑎 < 0, {𝑏 < 0, 𝑐 = 0. |
𝑎 > 0, {𝑏 < 0, 𝑐 > 0. |
𝑎 > 0, {𝑏 > 0, 𝑐 = 0. |
𝑎 < 0, {𝑏 > 0, 𝑐 < 0. |
𝑎 < 0, {𝑏 > 0, 𝑐 = 0. |
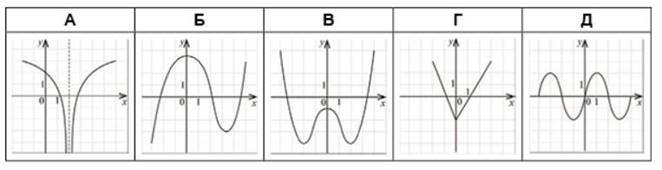
Укажіть рисунок, на якому зображено графік парної функції. № 11, 2009
На рисунку зображено точку, через яку проходить графік функції 𝑦 = 𝑓(𝑥). Укажіть функцію 𝑓(𝑥). № 10, 2008
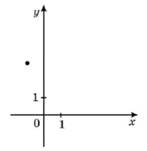
|
А |
Б |
В |
Г |
Д |
|
𝑓(𝑥) = −𝑥 |
𝑓(𝑥) = √𝑥 |
𝑓(𝑥) = log2 𝑥 |
𝑓(𝑥) = 𝑥3 |
𝑓(𝑥) = 3−𝑥 |
![]()
Укажіть область значень функції 𝑦 = √𝑥2 + 9 − 6 № 17, 2008
|
А |
Б |
В |
Г |
Д |
|
[9; +∞) |
[0; +∞) |
[3; +∞) |
[–3; +∞) |
(–∞; +∞) |
![]()
Знайдіть область визначення функції 𝑦 = √𝑥 + 9 № 5, 2007
|
А |
Б |
В |
Г |
Д |
|
[3; +∞) |
[9; +∞) |
[–3; +∞) |
[–9; +∞) |
[–9; 9] |
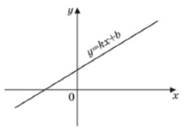
За видом графіка функції 𝑦 = 𝑘х + 𝑏визначте знаки коефіцієнтів 𝑘 і 𝑏. Оберіть
правильне твердження. № 9, 2007
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Укажіть парну функцію. № 10, 2007
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑥 |
𝑦 = 2𝑥 |
𝑦 = tg𝑥 |
𝑦 = log2 𝑥 |
𝑦 = 𝑥2 |
Укажіть непарну функцію №14, 2006
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑥2 − 4 |
𝑦 = −𝑥2 |
𝑦 = 𝑥3 − 1 |
𝑦 = √𝑥 − 2 |
𝑦 = 𝑥3 − 𝑥 |
Знайдіть область визначення функції ![]() . № 15, 2006
. № 15, 2006
|
А |
Б |
В |
Г |
Д |
|
[−2; 0) ∪ (0; +∞) |
[–2; +∞) |
(−2; 0) ∪ (0; +∞) |
(–∞; 2] |
𝑥 ≠ 1 |
Завдання на встановлення відповідності
Установіть відповідність між графіком (1–3) функції визначеної на проміжку [−4; 4] та її властивістю (А–Д). № 17, 2021
Графік функції
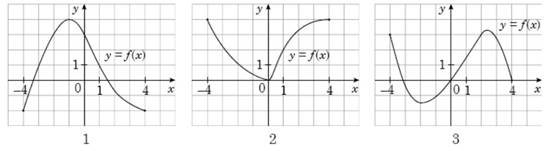
Властивість функції
|
А |
функція є непарною |
|
Б |
найменше значення функції на проміжку [1; 3] дорівнює 2 |
|
В |
функціє є парною |
|
Г |
графік функції не має спільних точок із графіком рівняння (𝑥 − 3)2 + (𝑦 − 4)2 = 4 |
|
Д
|
графік функції тричі перетинає пряму 𝑦 = 1 |
На рисунках (1–3) зображено графіки функцій, визначених на відрізку [−4; 4]. Установіть відповідність між графіком функції (1–3) та властивістю (А–Д), що має ця функція. № 21, 2020д
Графік функції
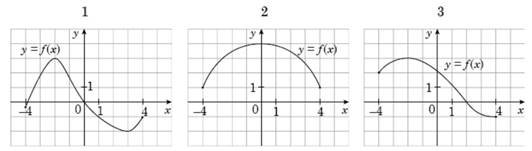
Властивість функції
|
А |
функція має лише один нуль |
|
Б |
функція є непарною |
|
В |
функціє немає точок екстремуму |
|
Г |
функція набуває лише додатних значень |
|
Д |
графік функції проходить через точку (3; −2) |
|
1 |
Функція 𝑦 = √𝑥 − 4 |
А |
спадає на проміжку (−∞; +∞) |
|
2 |
Функція 𝑦 = 𝑥 + 4 |
Б |
не визначена в точці 𝑥 = 1 |
|
3 |
Функція 𝑦 = 𝑥3 |
В |
є парною |
|
|
|
Г |
набуває додатного значення в точці 𝑥 = −3 |
|
|
|
Д |
є непарною |
![]() До кожного початку речення (1–3) доберіть його закінчення (А–Д) так, щоб утворилося
До кожного початку речення (1–3) доберіть його закінчення (А–Д) так, щоб утворилося
|
правильне речення. |
|
№ 21, 2020 |
|
Початок речення |
Закінчення речення |
|
Установіть відповідність між функцією (1–4) та її властивістю (А–Д). № 21, 2019д Функція Властивість
1 𝑦 = 𝑥2 А спадає на всій області визначення
2 𝑦 = 𝑥3 + 1 Б зростає на всій області визначення
3 𝑦 = 3 − 𝑥 В непарна
4 𝑦 = sin 𝑥 Г парна
Д область значень функції є проміжок (0; +∞)
До кожного речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося
|
правильне твердження. |
№ 21, 2019 |
|
Початок речення |
Закінчення речення |
|
1 графік функції 𝑦 = 1 |
А не перетинає вісь 𝑦 |
|
2 графік функції 𝑦 = cos 𝑥 |
Б є симетричним відносно початку координат |
|
3 графік функції 𝑦 = 4 − 𝑥2 |
В має безліч спільних точок з віссю 𝑥 |
|
4 графік функції 𝑦 = log3 𝑥 |
Г не має спільних точок з віссю 𝑥 |
|
|
Д проходить через точку (1; 3) |
На рисунках (1–4) зображено графіки функцій, кожна з яких визначена на проміжку [– 2; 2]. Установіть відповідність між графіками функцій (1–4) та властивостями (А–Д), що має ця функція. № 21, 2018д
Графік функції
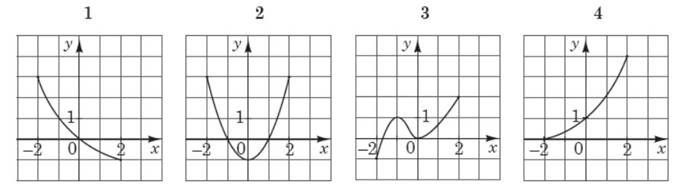
Властивість функції
|
А |
графік функції не перетинає графік функції 𝑦 = tg𝑥 |
|
Б |
графік функції є фрагментом графіка функції 𝑦 = 𝑥2 − 1 |
|
В |
множиною значень функції є проміжок [–1; 2] |
|
Г |
функція спадає на проміжку [–2; 2] |
|
Д |
функція зростає на проміжку [–2; 2] |
Установіть відповідність між функцією (1–4) та прямою, зображеною на рисунку (А–Д), яка не має з графіком цієї функції жодної спільної точки. № 21, 2017д Функція
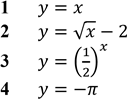
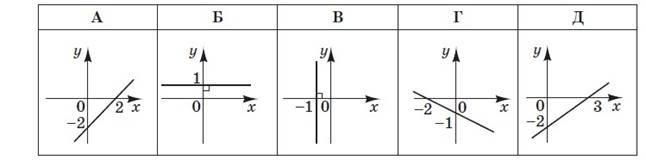
На рисунках (1–4) зображено графіки функцій, визначених на відрізку [–4; 4].
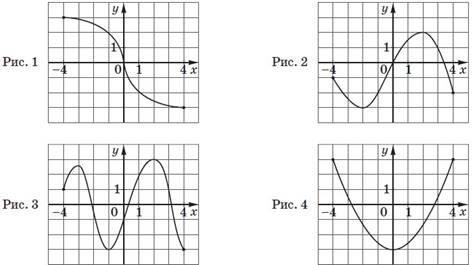
До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося
|
правильне твердження. |
№ 21, 2017 |
|
Початок речення |
Закінчення речення |
|
1 Функція, графік якої зображено на рис.1, |
А є непарною |
|
2 Функція, графік якої зображено на рис.2, |
Б набуває найбільшого |
|
3 Функція, графік якої зображено на рис.3, |
значення, що дорівнює 4 |
|
4 Функція, графік якої зображено на рис.4, |
В є парною |
|
|
Г має три нулі |
|
|
Д має дві точки локального |
|
|
екстремуму |
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥). визначеної на відрізку [–3; 4]. Установіть відповідність між функцією (1–4) та абсцисою (А–Д) точки перетину графіка цієї функції з графіком функції 𝑦 = 𝑓(𝑥). № 21, 2016д
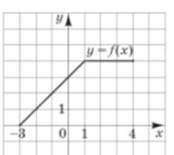
Функція Абсциса точки перетину
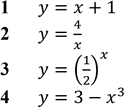 А х = –3
А х = –3
Б х = –1
В х = 0
Г х = 1
Д х = 3
На рисунках (1–5) зображено графіки функцій, визначених на відрізку [–3;3]. До кожного запитання (1–4) доберіть правильну відповідь (А–Д) № 21, 2016
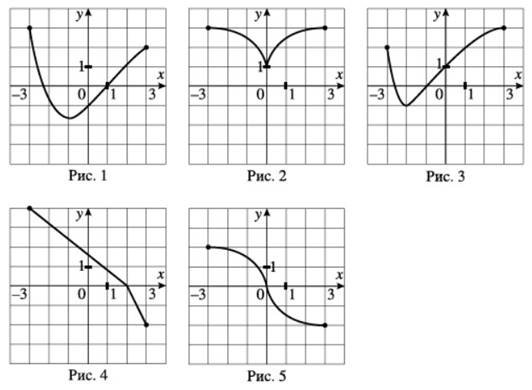
Запитання Відповідь
1 На якому рисунку зображено графік А рис. 1
парної функції? Б рис. 2
2 На якому рисунку зображено графік функції, В рис. 3
що проходить через точку (1; 0)? Г рис. 4
3 На якому рисунку зображено графік функції, Д рис. 5
що зростає на відрізку [–2; 3]?
4 На якому рисунку зображено графік функції,
що має дві спільні точки з графіком функції ![]()
До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося
|
правильне твердження. |
№ 23, 2015_ІІ |
|
Початок речення |
Закінчення речення |
|
1 Функція 𝑦 = 𝑥3 |
А набуває від'ємного значення в точці x = 8 |
|
2 Функція 𝑦 = (𝑥 + 2)2 − 3 |
Б не визначена в точці х = 1 |
|
3 Функція 𝑦 = log0,5 𝑥 |
В має екстремум у точці х = –2 |
![]()
4 Функція 𝑦 = √𝑥 − 4 Г набуває додатного значення в точці х = –3 Д є непарною
Установіть відповідність між функцією (1–4) та кількістю спільних точок (А–Д) графіка цієї функції з графіком функції![]() № 22, 2014
№ 22, 2014
Функція Кількість спільних точок
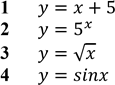 А жодної
А жодної
Б лише одна
В лише дві
Г лише три
Д більше трьох
На рисунку зображено графік функції у=f(x), визначеної на проміжку [0;11] та диференційованої на проміжку (0;11).
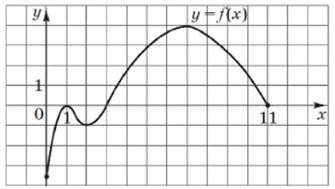
Установіть відповідність між числом (1-4) та проміжком (А—Д), якому належить це
|
число. |
№ 24, 2013_І |
|
Число |
Проміжок |
|
1 𝑓(8) |
А (–∞; –2] |
|
2 𝑓′(7) |
Б (–2; –0,5] |
|
3 найменше значення функції 𝑦 = 𝑓(𝑥) |
В (–0,5; 2] |
|
на її області визначення |
Г (2; 4] |
![]() Д (4; +∞)
Д (4; +∞)
Кожній точці (1–4) поставте у відповідність функцію (А–Д), графіку якої належить ця точка. № 22, 2012_І Точка Функція
1 𝑂(0; 0) А 𝑦 = 2𝑥 + 2
2 𝑀(0; −1) Б 𝑦 = 𝑐𝑡𝑔𝑥
3 𝑁(−1; 0) В 𝑦 = 𝑡𝑔𝑥
4 𝐾(0; 1) Г ![]() Д 𝑦 = 2𝑥
Д 𝑦 = 2𝑥
Установіть відповідність між функціями (1–4) та ескізами їхніх графіків (А–Д).
№ 26, 2011
Функція
1 𝑦 = tg𝑥
2 𝑦 = ctg𝑥
![]()
![]()
Ескіз графіка функції

Установіть відповідність між функціями, заданими формулами (1–4), та їхніми
|
властивостями (А–Д). |
|
№ 27, 2010_ІІ |
|
Функція |
Властивість функції |
|
|
Д |
періодична функція, що не має найменшого |
|
|
додатного періоду |
1 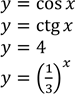 А областю визначення функції є інтервал (0; +∞)
А областю визначення функції є інтервал (0; +∞)
2 Б областю значень функції є відрізок [–1; 1] 3 В функція спадає на інтервалі (–∞; + ∞)
4 Г непарна функція
Установіть відповідність між функціями, заданими формулами (1–4), та їхніми властивостями (А–Д). № 27, 2010_І
Функція Властивість функції
1 𝑦 = 𝑥3 А областю визначення функції є проміжок [0; +∞)
2 𝑦 = cos 𝑥 Б функція спадає на інтервалі (0; +∞)
3 𝑦 = tg𝑥 В функція зростає на інтервалі (–∞; + ∞)
4 𝑦 = log0,2 𝑥 Г парна функція
Д періодична функція, з найменшим додатним
періодом 𝑇 = 𝜋
Завдання відкритої форми з короткою відповіддю
![]()
Знайдіть область визначення функції 𝑦 = 4√50 − 3𝑥. У відповіді запишіть найбільше ціле двоцифрове число, що належить області визначення цієї функції. № 27, 2017д
Знайдіть область визначення функції ![]() . У відповіді запишіть найбільше ціле двоцифрове число, що належить області визначення цієї функції. № 27, 2017
. У відповіді запишіть найбільше ціле двоцифрове число, що належить області визначення цієї функції. № 27, 2017
![]()
Графік функції 𝑦 = √2𝑥2 + 𝑥 + 1 проходить через точку (𝑥0; 4), де 𝑥0 > 0. Обчисліть 𝑥0.
№ 28, 2014д
Завдання відкритої форми з розгорнутою відповіддю
Задано функції ![]() .
.
Завдання (1–3) виконайте на одному рисунку.
1. Побудуйте графік функції 𝑓.
2. Побудуйте графік функції 𝑔 на проміжку ![]() .
.
3. Позначте на рисунку точку, що є спільною для обох побудованих графіків функцій 𝑓 і 𝑔, і запишіть її координати.
4. Знайдіть множину всіх коренів рівняння 𝑓(𝑥) = 𝑔(𝑥) на інтервалі (−∞; +∞).
№ 33, 2020д
Задано функції 𝑓(𝑥) = 1 та 𝑔(𝑥) = sin 𝑥.
Завдання (1–3) виконайте на одному рисунку.
1. Побудуйте графік функції 𝑓.
2. Побудуйте графік функції 𝑔 на проміжку ![]() .
.
3. Позначте на рисунку точку, що є спільною для обох побудованих графіків функцій 𝑓 і 𝑔, і запишіть її координати.
4. Знайдіть множину всіх коренів рівняння 𝑓(𝑥) = 𝑔(𝑥) на інтервалі (−∞; +∞).
№ 33, 2020
ЕЛЕМЕНТАРНІ ПЕРЕТВОРЕННЯ ГРАФІКІВ ФУНКЦІЇ
Завдання з вибором однієї правильної відповіді
Укажіть з поміж наведених ескіз графіка функції 𝑦 = −2𝑥 + 3. № 7, 2021
Укажіть з поміж наведених функцію, ескіз графіка якої зображений на рисунку.
№ 14, 2020д
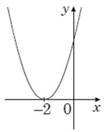
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑥2 − 2 |
𝑦 = (𝑥 − 2)2 |
𝑦 = 𝑥2 |
𝑦 = (𝑥 + 2)2 |
𝑦 = 𝑥2 + 2 |
Графік довільної функції 𝑦 = 𝑓(𝑥) паралельно перенесли вздовж осі 𝑦 на 3 одиниці вниз.
Графік якої з наведених функцій отримали. № 13, 2020
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑓(𝑥 + 3) |
𝑦 = 𝑓(𝑥) + 3 |
𝑦 = 3𝑓(𝑥) |
𝑦 = 𝑓(𝑥) − 3 |
𝑦 = 𝑓(𝑥 − 3) |
Графік довільної функції 𝑦 = 𝑓(𝑥) паралельно перенесли вздовж осі 𝑥 на 2 одиниці праворуч. Графік якої з наведених функцій отримали. № 12, 2019д
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑓(𝑥 + 2) |
𝑦 = 𝑓(𝑥) + 2 |
𝑦 = 2𝑓(𝑥) |
𝑦 = 𝑓(𝑥) − 2 |
𝑦 = 𝑓(𝑥 − 2) |
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥), визначеної на проміжку [–3;3]. Одна з наведених точок належить графіку функції 𝑦 = −𝑓(𝑥). Укажіть цю точку. № 15, 2019
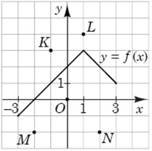
|
А |
Б |
В |
Г |
Д |
|
K |
L |
O |
M |
N |
Укажіть ескіз графіка функції 𝑦 = 𝑥3 − 1 № 9, 2018д
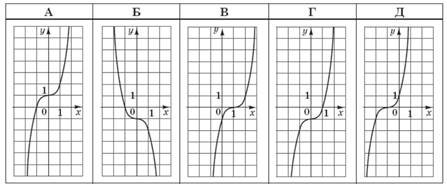
На рисунку зображено фрагмент графіка однієї з наведених функцій на проміжку
![]() . Укажіть цю функцію. № 9, 2017д
. Укажіть цю функцію. № 9, 2017д
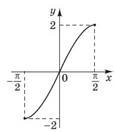
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 2𝑠𝑖𝑛𝑥 |
|
𝑦 = −2𝑠𝑖𝑛𝑥 |
|
𝑦 = 2𝑐𝑜𝑠𝑥 |
На одному з рисунків зображено графік функції 𝑦 = 1 − 𝑥2. Укажіть цей рисунок.
№ 11, 2017
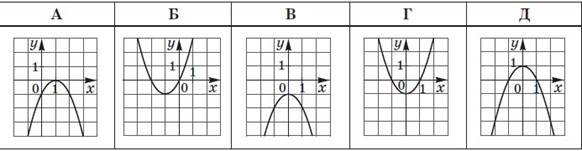
Укажіть функцію, графіком якої є парабола з вершиною в точці (–2; 0) № 14, 2016д
|
А |
Б |
В |
Г |
Д |
|
𝑦 = 𝑥2 − 2 |
𝑦 = (𝑥 − 2)2 |
𝑦 = (𝑥 + 2)2 |
𝑦 = −2𝑥2 |
𝑦 = 𝑥2 + 2 |
Графік функції 𝑦 = 𝑠𝑖𝑛𝑥 можна отримати внаслідок паралельного перенесення графіка функції 𝑦 = 𝑐𝑜𝑠𝑥 уздовж осі х. № 18, 2016д
|
А |
Б |
В |
Г |
Д |
|
вправо 𝜋 на одиниць 2 |
вправо на 𝜋 одиниць |
вправо 3𝜋 на одиниць 2 |
вліво на 𝜋 одиниць |
вліво 𝜋 на одиниць 2 |
Яка з наведених парабол може бути графіком функції 𝑦 = 𝑥2 + 𝑝𝑥 + 𝑞, якщо рівняння
𝑥2 + 𝑝𝑥 + 𝑞 = 0 не має дійсних коренів? № 15, 2016
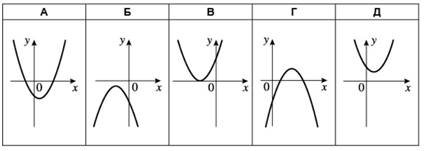
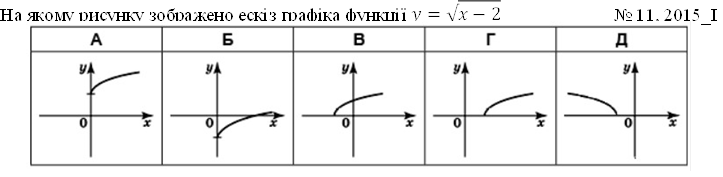
На якому з рисунків зображено фрагмент графіка функції 𝑦 = cos (𝑥 + 2𝜋) на проміжку
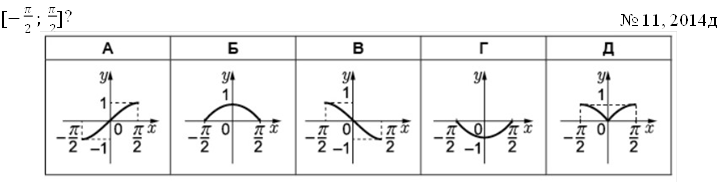
На рисунку зображено графік функції 𝑦 = 𝑥2 − 2𝑥. Укажіть графік функції
𝑦 = |𝑥2 − 2𝑥|. № 10, 2013_ІІ
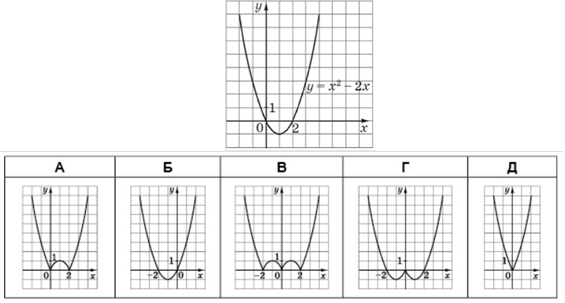
Укажіть ескіз графіка функції 𝑦 = 𝑥3 − 1 № 4, 2013_І
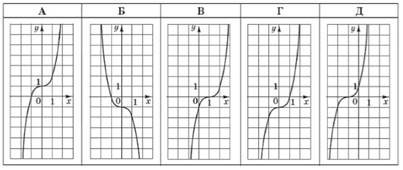
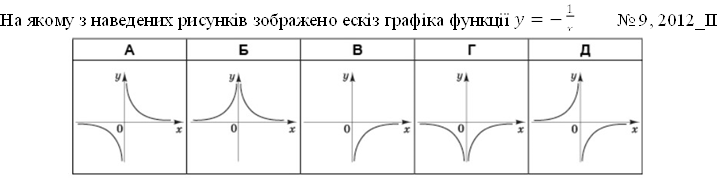
На якому з наведених рисунків зображено ескіз графіка функції 𝑦 = 4 − (𝑥 − 1)2
№ 10, 2012_І
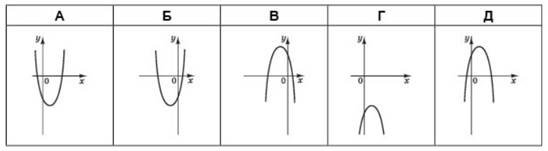
На одному з рисунків зображено ескіз графіка функції 𝑦 = − log4 𝑥. Укажіть цей рисунок. № 20, 2010_ІІ
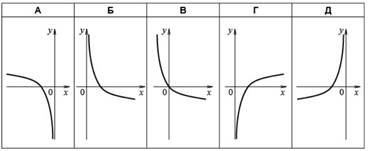
У прямокутній системі координат зображено точку, що є вершиною параболи 𝑦 = 𝑥2 + 𝑏𝑥 + 𝑐 (див. рисунок). Укажіть правильне твердження щодо коефіцієнтів 𝑏 і 𝑐.
№ 25, 2010_ІІ
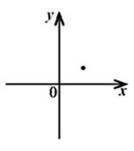
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
На рисунку зображено ескіз графіка функції 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐. Укажіть правильне твердження щодо коефіцієнтів 𝑎, 𝑏 і 𝑐. № 25, 2010_І
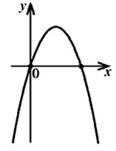
|
А |
Б |
В |
Г |
Д |
|
𝑎 < 0, {𝑏 < 0, 𝑐 = 0. |
𝑎 > 0, {𝑏 < 0, 𝑐 > 0. |
𝑎 > 0, {𝑏 > 0, 𝑐 = 0. |
𝑎 < 0, {𝑏 > 0, 𝑐 < 0. |
𝑎 < 0, {𝑏 > 0, 𝑐 = 0. |
Графік функції 𝑦 = 𝑓(𝑥) проходить через точку 𝑀(1; 1) (див. рисунок). При якому значенні 𝑎 графік функції 𝑦 = 𝑓(𝑥) + 𝑎 проходить через точку 𝑁(1; 3)? № 16, 2009
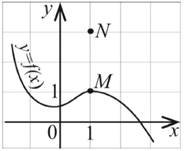
|
А |
Б |
В |
Г |
Д |
|
2 |
–2 |
такого значення не існує |
|
3 |
З-поміж наведених графіків укажіть графік функції 𝑦 = −|𝑥 + 3| № 5, 2006

Серед наведених графіків вкажіть графік функції 𝑦 = 3 − (𝑥 + 1)2 № 3, 2005
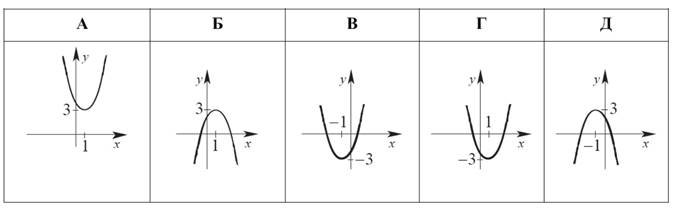
Завдання на встановлення відповідності
До кожного початку речення (1–4) доберіть його закінчення (А – Д), так щоб утворилося
|
правильне твердження. |
№ 21, 2018 |
|
Початок речення |
Закінчення речення |
|
1 Пряма 𝑦 = 4,5𝑥 |
А є паралельною прямій 𝑦 = 2𝑥 |
|
2 Пряма 𝑦 = −4 |
Б не має спільних точок з графіком функції 𝑦 = 𝑥2 − 1 |
|
3 Пряма 𝑦 = 2𝑥 + 4 |
В перетинає графік функції 𝑦 = 3𝑥 у точці з абсцисою 𝑥0 = 2 |
|
4 Пряма 𝑦 = 𝑥 |
Г є паралельною осі у |
|
|
Д є бісектрисою І і ІІІ координатних чвертей |
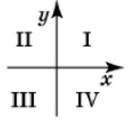
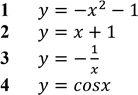 Установіть відповідність між функцією (1–4) та координатними чвертями (А–Д), у яких розміщений графік цієї функції (координатні чверті показано на рисунку). № 21, 2015_І
Установіть відповідність між функцією (1–4) та координатними чвертями (А–Д), у яких розміщений графік цієї функції (координатні чверті показано на рисунку). № 21, 2015_І
Функція Координатні чверті
А II та IV
Б III та IV
В І, ІІ та ІІІ
Г I, III та IV
Д I, II, III та IV
Установіть відповідність між твердженням (1–4) та функцією (А–Д), для якої це
|
твердження є правильним. |
|
№ 23, 2014д |
|
Твердження |
Функція |
|
1 графік функції проходить через точку (0; 1) А ![]()
2 найменшого значення функція набуває в точці 𝑥 = −2 Б 𝑦 = (𝑥 + 2)2
3 областю визначення функції є множина В 𝑦 = 3𝑥
(−∞; 2) ∪ (2; +∞) Г 𝑦 = |𝑥|
4 графік функції симетричний відносно осі 𝑦 Д 𝑦 = 𝑥3
Установіть відповідність між твердженням (1–4) та функцією (А–Д), для якої це твердження є правильним. № 22, 2013_ІІ
Твердження Функція
1 графік функції не перетинає жодну з осей координат А 𝑦 = −𝑥 + 2
2 областю значень функції є проміжок (0; +∞) Б 𝑦 = 𝑥2 − 2
3 функція спадає на всій області визначення В ![]()
|
4 |
на відрізку [–1,5; 1,5] функція має два нулі |
Г |
𝑦 = 3𝑥 |
|
|
|
Д |
𝑦 = 𝑐𝑜𝑠𝑥 |
На рисунку зображено графік функції у = 𝑓(𝑥), спадної на проміжку (−∞; +∞). Установіть відповідність між функцією (1–4) та точкою перетину її графіка з віссю Ох (А–Д).
№ 24, 2012_ІІ
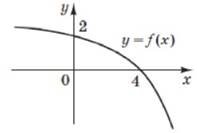
|
Функція |
Точка перетину |
|
1 𝑦 = 𝑓(𝑥 + 2) |
А (0; 0) |
|
2 𝑦 = 𝑓(𝑥 − 2) |
Б (2; 0) |
|
3 𝑦 = 2𝑓(𝑥) |
В (4; 0) |
|
4 𝑦 = 𝑓(𝑥) − 2 |
Г (6; 0) |
|
|
Д (8; 0) |
Завдання відкритої форми з короткою відповіддю
На рисунку зображено графік функції 𝑓(𝑥) = 𝑥4 − 𝑥2 + 𝑏𝑥 + 𝑐. Визначте знаки параметрів 𝑏 і 𝑐. № 32, 2006
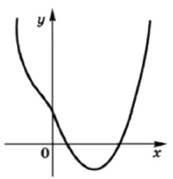
У відповіді вкажіть номер правильного варіанта з наведених нижче.
|
1 |
2 |
3 |
4 |
|
|
|
|
|
𝑎𝑥+𝑏
За ескізом графіка функції ![]() визначіть знаки параметрів 𝑎, 𝑏, 𝑐. № 22, 2005
визначіть знаки параметрів 𝑎, 𝑏, 𝑐. № 22, 2005
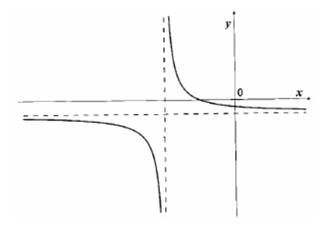
У відповіді вкажіть номер правильного варіанта з наведених нижче.
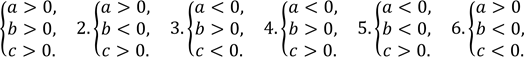 ,
,
1.
Завдання відкритої форми з розгорнутою відповіддю
Побудуйте графік функції 𝑦 = 2log2(5𝑥−𝑥2) Користуючись графіком, визначте область значень цієї функції. № 31, 2016д
Побудуйте графік функції ![]() Користуючись графіком, визначте область значень цієї функції. № 31, 2016
Користуючись графіком, визначте область значень цієї функції. № 31, 2016
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ВІДНОШЕННЯ І ПРОПОРЦІЇ
Завдання з вибором однієї правильної відповіді
За 6 однакових конвертів заплатили 3 гри. Скільки всього таких конвертів можна купити за 12 грн? № 1, 2021
|
А |
Б |
В |
Г |
|
6 |
24 |
30 |
36 |
Копіювальна машина робить 3 копії за 4 секунди. Яку максимальну кількість копій можна одержати за 1 хвилину? № 3, 2020
|
А |
Б |
В |
Г |
Д |
|
45 |
60 |
75 |
80 |
120 |
Два фахівці розробили макет рекламного оголошення. За роботу вони отримали 3000 грн і розподілили гроші таким чином: перший отримав четверту частину зароблених грошей, а другий - решту. Скільки гривень отримав за цю роботу другий фахівець? № 3, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
600 грн |
750 грн |
1800 грн |
2250 грн |
2400 грн |
Сергій і Петро збирали яблука. Сергій зібрав яблук у 5 разів більше, ніж Петро. Яку частину всіх яблук зібрав Петро? № 5, 2015_І
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
𝑚 3
Визначте т із співвідношення = ![]() , де 𝑛 ≠ 0 № 1, 2013_І
, де 𝑛 ≠ 0 № 1, 2013_І
2 𝑛
|
А |
Б |
В |
Г |
Д |
|
𝑚 = 6𝑛 |
|
|
|
|
Протягом тижня два кур'єри разом доставили 210 пакетів. Кількості пакетів, доставлених першим і другим кур'єрами за цей період, відносяться як 3:7. Скільки пакетів доставив другий кур'єр? № 2, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
21 |
30 |
63 |
70 |
147 |
Два фахівці розробили макет рекламного оголошення. За роботу вони отримали 5000 грн, розподіливши гроші таким чином: перший отримав четверту частину зароблених грошей, а другий – решту. Скільки гривень отримав за цю роботу другий фахівець?
№ 6, 2012_І
|
А |
Б |
В |
Г |
Д |
|
1000 грн |
1250 грн |
3000 грн |
3750 грн |
4000 грн |
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
Будівельна компанія закупила для нового будинку металопластикові вікна та двері у відношенні 4:1. Укажіть число, яким може виражатися загальна кількість вікон та дверей в цьому будинку. № 6, 2007
|
А |
Б |
В |
Г |
Д |
|
41 |
45 |
54 |
68 |
81 |
Завдання відкритої форми з короткою відповіддю
Для приготування дезінфікувального розчину концентрат розводять водою в масовому відношенні 2:7 відповідно, після чого на 10 г води добавляють 1 г ароматичної рідини. Скільки грамів концентрату потрібно для приготування 485 г розчину? № 26, 2021
Для приготування чайної суміші змішали індійський та цейлонський чай у відношенні 10:13, причому індійського чаю взяли 180г.
1. Скільки грамів чайної суміші отримали?
2. На скільки відсотків у суміші цейлонського чаю більше, ніж індійського?
№ 25, 2017д
Відомо, що ![]() , де 0 < x < у. У скільки разів число у більше за число x? № 27, 2014
, де 0 < x < у. У скільки разів число у більше за число x? № 27, 2014
ПОХІДНА. РІВНЯННЯ ДОТИЧНОЇ.
ГЕОМЕТРИЧНИЙ ТА ФІЗИЧНИЙ ЗМІСТ ПОХІДНОЇ
Завдання з вибором однієї правильної відповіді
Укажіть похідну функції ![]() № 18, 2018д
№ 18, 2018д
А ![]()
|
Б |
𝑦′ = −7𝑥5 + 20𝑥3 − 14 |
|
В |
𝑦′ = −7𝑥5 + 20𝑥3 |
|
Г |
𝑦′ = −7𝑥7 + 25𝑥5 |
Д ![]()
Укажіть похідну функції 𝑓(𝑥) = 𝑥(𝑥3 + 1) № 19, 2018
|
А |
Б |
В |
Г |
Д |
|
𝑓′(𝑥)=4𝑥3 +1 |
𝑓′(𝑥)=4𝑥3 |
𝑓′(𝑥)=3𝑥2 |
𝑓′(𝑥)=3𝑥2 +1 |
|
Укажіть похідну функції 𝑦 = 𝑠𝑖𝑛𝑥 − 𝑐𝑜𝑠𝑥 + 1 № 20, 2017
|
А |
𝑦′ = 𝑐𝑜𝑠𝑥 + 𝑠𝑖𝑛𝑥 + 1 |
|
Б |
𝑦′ = 𝑐𝑜𝑠𝑥 − 𝑠𝑖𝑛𝑥 |
|
В |
𝑦′ = −𝑐𝑜𝑠𝑥 − 𝑠𝑖𝑛𝑥 + 𝑥 |
|
Г |
𝑦′ = −𝑐𝑜𝑠𝑥 − 𝑠𝑖𝑛𝑥 |
|
Д |
𝑦′ = 𝑐𝑜𝑠𝑥 + 𝑠𝑖𝑛𝑥 |
Якщо ![]() № 19, 2015_ІІ
№ 19, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
3(4𝑥 − 1)2 |
3(4𝑥 − 1) |
(4𝑥 − 1)4
16 |
12(4𝑥 − 1)2 |
|
Укажіть рівняння прямої, яка може бути дотичною до графіка функції 𝑦 = 𝑓(𝑥) у точці з абсцисою 𝑥0 = 2, якщо 𝑓′(2) = −3. № 19, 2015_І
|
А |
Б |
В |
Г |
Д |
|
|
𝑦 = 3𝑥 − 2 |
𝑦 = 2𝑥 + 3 |
|
𝑦 = −3𝑥 + 2 |
Укажіть рівняння дотичної, проведеної до графіка функції 𝑦 = 𝑓(𝑥) у точці з абсцисою
𝑥0 = 1, якщо 𝑓(𝑥) = 5, 𝑓′(𝑥0) = 2 № 20, 2014
|
А |
Б |
В |
Г |
Д |
|
𝑦=1+2(𝑥−5) |
𝑦 =5+2(𝑥+1) |
𝑦 =2+5(𝑥−1) |
𝑦 =2+5(𝑥+1) |
𝑦 =5+2(𝑥−1) |
Знайдіть похідну функції 𝑦 = 𝑒−2𝑥 № 18, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
𝑦′ = 𝑒−2𝑥 |
𝑦′ = −2𝑒−2𝑥 |
𝑦′ = −2𝑥𝑒−2𝑥−1 |
𝑦′ = 2𝑒−2𝑥 |
|
Функція 𝑓(𝑥)має в точці 𝑥0 = 5 похідну 𝑓′(𝑥0) = −1. Обчисліть значення похідної функції 𝑔(𝑥) = 𝑓(𝑥) ∙ 𝑥 в точці 𝑥0, якщо 𝑓(5) = 3. № 20, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
𝑔′(5) = −2 |
𝑔′(5) = −1 |
𝑔′(5) = −5 |
𝑔′(5) = 14 |
𝑔′(5) = 15 |
Функція 𝑓(𝑥)має в точці 𝑥0похідну 𝑓′(𝑥0) = −4. Визначте значення похідної функції
𝑔(𝑥) = 2 ∙ 𝑓(𝑥) + 7𝑥 − 3 в точці 𝑥0. № 20, 2012_І
|
А |
Б |
В |
Г |
Д |
|
15 |
12 |
–1 |
–4 |
–8 |
Знайдіть значення похідної функції 𝑓(𝑥) = 2𝑥3 − 5 у точці 𝑥0 = −1 № 19, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
–11 |
–7 |
1 |
3 |
6 |
Знайдіть значення похідної функції 𝑓(𝑥) = 4 cos 𝑥 + 5 у точці 𝑥0 = 𝜋![]() 2 № 17, 2010_І
2 № 17, 2010_І
|
А |
Б |
В |
Г |
Д |
|
–4 |
–1 |
1 |
4 |
5 |
Знайдіть похідну функції 𝑦 = 𝑥4 + 3 cos 𝑥. № 14, 2009
А 𝑦′ = 4𝑥3 + 3 sin 𝑥
Б 𝑦′ = 4𝑥 − 3 sin 𝑥
В ![]()
Г ![]()
Д 𝑦′ = 𝑥3 − 3 sin 𝑥
Тіло рухається прямолінійно за законом ![]() (час t вимірюється у секундах, шлях s – у метрах). Визначте прискорення його руху у момент 𝑡 = 10 с.
(час t вимірюється у секундах, шлях s – у метрах). Визначте прискорення його руху у момент 𝑡 = 10 с.
№ 21, 2008
|
А |
Б |
В |
Г |
Д |
|
164 м/с2 |
60 м/с2 |
36 м/с2 |
20 м/с2 |
10 м/с2 |
На рисунку зображений графік функції 𝑦 = 𝑓(𝑥) та дотичні до нього в точках 𝑥1та 𝑥2.
Користуючись геометричним змістом похідної, знайдіть 𝑓′(𝑥1) + 𝑓′(𝑥2). № 16, 2007
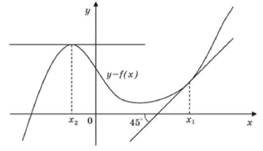
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
На рисунку зображено графік функції 𝑦 = 𝑓(𝑥) і дотичну до нього у точці з абсцисою 𝑥0.
№ 11, 2006
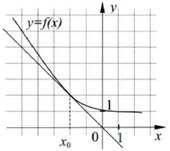
Знайдіть значення 𝑓′(𝑥0)
|
А |
Б |
В |
Г |
Д |
|
–2 |
–1 |
0 |
1 |
2 |
Завдання відкритої форми з короткою відповіддю
Матеріальна точка рухається прямолінійно за законом 𝑠(𝑡) = 4𝑡2 + 9𝑡 + 8 (шлях s вимірюється в метрах, час t – у секундах). Визначте швидкість (у м/с) цієї точки в момент часу 𝑡 = 4 с. № 27, 2016д
Обчисліть значення похідної функції ![]() у точці 𝑥0 = 3. № 27, 2016
у точці 𝑥0 = 3. № 27, 2016
Матеріальна точка рухається за законом 𝑠(𝑡) = 2𝑡2 + 3𝑡, де 𝑠вимірюється в метрах, a 𝑡– у секундах. Знайдіть значення 𝑡(у секундах), при якому миттєва швидкість матеріальної точки дорівнює 76 м/с. № 30, 2011
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ДОСЛІДЖЕННЯ ФУНКЦІЇ. ПОБУДОВА ГРАФІКА ФУНКЦІЇ
Завдання з вибором однієї правильної відповіді
На рисунку зображено графік неперервної функції у = 𝑓(𝑥), визначеної на відрізку
[– 3; 7]. Скільки всього точок екстремуму має ця функція на відрізку [– 3; 7]?
№ 5, 2013_ІІ
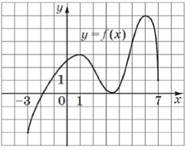
|
А |
Б |
В |
Г |
Д |
|
1 |
2 |
3 |
5 |
6 |
Знайдіть критичні точки функції 𝑦 = 𝑥3 − 3𝑥2 + 5 № 5, 2005
|
А |
Б |
В |
Г |
Д |
|
1; 2 |
−1; 0 |
0; 2 |
−1; 2 |
−2; 1 |
Завдання відкритої форми з короткою відповіддю Задано функцію 𝑓(𝑥) = 3𝑥4 − 4𝑥3 − 12𝑥2.
1. Знайдіть проміжки зростання та спадання функції, екстремуми функції.
2. Побудуйте ескіз графіка функції 𝑓(𝑥).
3. Знайдіть кількість коренів рівняння 𝑓(𝑥) = 𝑎, де 𝑎 ∈ 𝑅, залежно від значення параметра 𝑎.
У відповідь запишіть найбільше ціле 𝑎, при якому рівняння не має коренів. Якщо такого значення не існує, у відповідь запишіть число 100. № 36, 2008
Знайдіть найбільше значення функції 𝑦 = 𝑥3 − 3𝑥2 + 2 на проміжку [–1; 1]
№ 31, 2007
Відрізок 12 см завдовжки поділили на дві частини так, що сума площ квадратів, побудованих на цих частинах, стала найменшою. Обчисліть суму площ квадратів.
№ 29, 2006
Завдання відкритої форми з розгорнутою відповіддю Задано функцію 𝑦 = 𝑥3 − 12𝑥.
1. Для наведених у таблиці значень аргумента 𝑥 визначте відповідні їм значення 𝑦.
|
𝑥 |
𝑦 |
|
−1 |
|
|
0 |
|
|
2 |
|
2. Визначте й запишіть координати точок перетину графіка функції 𝑦 = 𝑥3 − 12𝑥 із віссю 𝑥.
3. Знайдіть похідну 𝑓′ функції 𝑓(𝑥) = 𝑥3 − 12𝑥
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
4. Визначте нулі функції 𝑓′
5. Визначте проміжки зростання і спадання, точки екстремуму й екстремуми функції 𝑓
6. Побудуйте ескіз графіка функції 𝑓 № 30, 2021д
Задано функцію 𝑦 = 𝑥3 − 3𝑥.
1. Для наведених у таблиці значень аргумента 𝑥 визначте відповідні їм значення 𝑦.
|
𝑥 |
𝑦 |
|
0 |
|
|
−1 |
|
|
2 |
|
2. Визначте й запишіть координати точок перетину графіка функції 𝑦 = 𝑥3 − 3𝑥 із віссю 𝑥.
3. Знайдіть похідну 𝑓′ функції 𝑓(𝑥) = 𝑥3 − 3𝑥
4. Визначте нулі функції 𝑓′
5. Визначте проміжки зростання і спадання, точки екстремуму й екстремуми функції 𝑓
6. Побудуйте ескіз графіка функції 𝑓 № 30, 2021
Задано функції ![]() .
.
1. Побудуйте графік функції 𝑓.
2. Побудуйте графік функції 𝑔.
3. Знайдіть похідну функції 𝑓.
4. До графіка функції 𝑓 проведено дотичні, паралельні графіку функції 𝑔. Визначте абсциси точок дотику. № 31, 2019д
Задано функції ![]() .
.
1. Побудуйте графік функції 𝑓.
2. Побудуйте графік функції 𝑔.
3. Знайдіть похідну функції 𝑓.
4. До графіка функції 𝑓 проведено дотичні, паралельні графіку функції 𝑔. Визначте абсциси точок дотику. № 31, 2019
Задано функцію 𝑓(𝑥) = 𝑥2 + 3𝑥 − 10.
1. Визначте координати точок перетину графіка функції 𝑓 з осями координат.
2. Побудуйте графік функції 𝑓.
3. Знайдіть похідну функції 𝑓.
4. Визначте кутовий коефіцієнт дотичної, проведеної до графіка функції 𝑓 у точці з абсцисою 𝑥0 = −1. № 31, 2017д
Задано функцію ![]() .
.
Знайдіть:
а) область визначення функції;
б) нулі функції 𝑓(𝑥);
в) всі розв’язки нерівності ![]() . № 26, 2005
. № 26, 2005
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 3
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
ПЕРВІСНА. ІНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНІЦА
Завдання з вибором однієї правильної відповіді
Яка з наведених функцій є первісною для функції 𝑓(𝑥) = 𝑥−4. № 11, 2021
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Функція 𝐹(𝑥) = 10𝑥5 − 4 є первісної функції 𝑓(𝑥). Укажіть функцію 𝐺(𝑥), яка є також первісною функції 𝑓(𝑥). № 18, 2020д
|
А |
Б |
В |
Г |
Д |
|
𝐺(𝑥) = 10𝑥5 + 7 |
𝐺(𝑥) = 2𝑥6 − 4𝑥 |
𝐺(𝑥) = 50𝑥6 |
𝐺(𝑥) = 50𝑥4 |
𝐺(𝑥) = 𝑥5 − 4 |
Функція 𝐹(𝑥) = 5𝑥4 − 1 є первісної функції 𝑓(𝑥). Укажіть функцію 𝐺(𝑥), яка є також первісною функції 𝑓(𝑥). № 20, 2020
|
А |
Б |
В |
Г |
Д |
|
𝐺(𝑥) = 𝑥5 − 𝑥 |
𝐺(𝑥) = 5𝑥4 − 𝑥 |
𝐺(𝑥) = 20𝑥3 |
𝐺(𝑥) = 5𝑥4 + 1 |
𝐺(𝑥) = 𝑥4 − 5 |
Обчисліть інтеграл ∫02(𝑓(𝑥) + 6)𝑑𝑥, якщо ∫02 𝑓(𝑥)𝑑𝑥 = 8. № 18, 2017д
|
А |
Б |
В |
Г |
Д |
|
20 |
14 |
2 |
28 |
48 |
Використовуючи формулу Ньютона – Лейбніца, обчисліть ![]() № 19, 2016
№ 19, 2016
|
А |
Б |
В |
Г |
Д |
|
42 |
22 |
18 |
14 |
12 |
Функція 𝐹(𝑥) = 6 sin(2𝑥) − 1 є первісною функції 𝑓(𝑥). Знайдіть функцію 𝑓(𝑥).
|
|
|
№ 24, 2011 |
|
А |
𝑓(𝑥) = −12 cos(2𝑥) |
|
|
Б |
𝑓(𝑥) = 6 cos(2𝑥) |
|
|
В |
𝑓(𝑥) = 12 cos(2𝑥) |
|
|
Г |
𝑓(𝑥) = −3 cos(2𝑥) − 𝑥 + 𝐶 |
|
|
Д |
𝑓(𝑥) = −6 cos(2𝑥) − 𝑥 + 𝐶 |
|
Знайдіть первісну функції 𝑓(𝑥) = 2𝑥 + 2, графік якої проходить через точку з координатами (1; 4). № 15, 2007
А 𝐹(𝑥) = 𝑥2 + 2𝑥
Б 𝐹(𝑥) = 𝑥2 + 2𝑥 + 1
В 𝐹(𝑥) = 𝑥2 + 2𝑥 + 2
Г 𝐹(𝑥) = 𝑥2 + 2𝑥 − 4
Д 𝐹(𝑥) = 𝑥2 + 2𝑥 − 23
Завдання відкритої форми з короткою відповіддю
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
На рисунку зображено графік функції 𝐹(𝑥) = 𝑥2 + 𝑏𝑥 + 𝑐, яка є первісною для функції 𝑓(𝑥). Визначте параметри 𝑏 і 𝑐, знайдіть функцію 𝑓(𝑥). У відповіді запишіть значення 𝑓(−8).
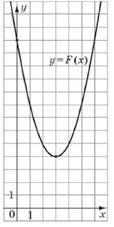 № 31, 2013_І
№ 31, 2013_І
Обчисліть ![]() використовуючи зображений на рисунку графік лінійної функції у
використовуючи зображений на рисунку графік лінійної функції у
= f(x).
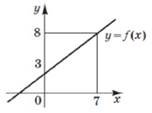 № 30, 2012_ІІ
№ 30, 2012_ІІ
Обчисліть ![]() , використовуючи рівняння кола 𝑥2 + 𝑦2 = 25, зображеного
, використовуючи рівняння кола 𝑥2 + 𝑦2 = 25, зображеного
на рисунку
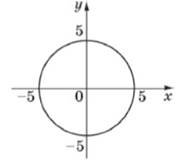 № 30, 2012_І
№ 30, 2012_І
Обчисліть інтеграл ![]() . № 32, 2010_І
. № 32, 2010_І
КРИВОЛІНІЙНА ТРАПЕЦІЯ
Завдання з вибором однієї правильної відповіді
У прямокутній системі координат на площині зображено план паркової зони, що має форму фігури, обмеженої графіками функцій 𝑦 = 𝑓(𝑥) і 𝑦 = 3 (див. рисунок). Укажіть формулу для обчислення площі 𝑆 цієї фігури. № 13, 2021д
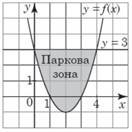
|
А |
Б |
В |
Г |
Д |
|
3 𝑆 = ∫(𝑓(𝑥)−3)𝑑𝑥 |
3 𝑆= ∫(3−𝑓(𝑥))𝑑𝑥 |
4 𝑆 =∫(𝑓(𝑥)+3)𝑑𝑥 0 |
4 𝑆 =∫(𝑓(𝑥)−3)𝑑𝑥 0 |
4 𝑆 =∫(3−𝑓(𝑥))𝑑𝑥 0 |
−1 −1
На рисунку зображено графіки функцій ![]() . Укажіть формулу для обчислення площі зафарбованої фігури. № 18, 2019д
. Укажіть формулу для обчислення площі зафарбованої фігури. № 18, 2019д
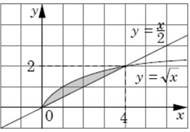
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
На рисунку зображено графіки функцій 𝑦 = 𝑓(𝑥) і 𝑦 = 𝑔(𝑥). Укажіть формулу для обчислення площі зафарбованої фігури. № 18, 2019
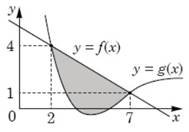
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
На рисунку зображено графіки функцій 𝑦 = 𝑓(𝑥) і 𝑦 = 𝑔(𝑥). Укажіть формулу для обчислення площі зафарбованої фігури. № 20, 2016д
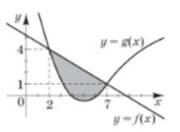
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
На рисунку зображено графік неперервної функції у = 𝑓(𝑥). Укажіть формулу для обчислення площі зафарбованої фігури. № 19, 2014д
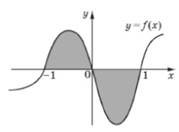
|
А |
Б |
В |
Г |
Д |
|
1 ∫𝑓(𝑥)𝑑𝑥 −1 |
1 2∫𝑓(𝑥)𝑑𝑥 0 |
1 0 ∫𝑓(𝑥)𝑑𝑥− ∫𝑓(𝑥)𝑑𝑥 0 −1 |
0 2 ∫𝑓(𝑥)𝑑𝑥 −1 |
0 1 ∫𝑓(𝑥)𝑑𝑥−∫𝑓(𝑥)𝑑𝑥 −1 0 |
На рисунку зображено графік функції у = 𝑓(𝑥). Укажіть формулу для обчислення площі зафарбованої фігури. № 19, 2008
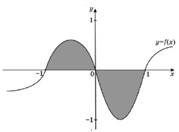
|
А |
Б |
В |
Г |
Д |
|
1 ∫ 𝑓(𝑥)𝑑𝑥 −1 |
0 1 ∫ 𝑓(𝑥)𝑑𝑥 − ∫ 𝑓(𝑥)𝑑𝑥 −1 0 |
1 0 ∫ 𝑓(𝑥)𝑑𝑥 − ∫ 𝑓(𝑥)𝑑𝑥 0 −1 |
0 2 ∫ 𝑓(𝑥)𝑑𝑥 −1 |
1 2 ∫ 𝑓(𝑥)𝑑𝑥 0 |
Вкажіть формулу для обчислення площі фігури, обмеженої графіками функцій
𝑦 = 𝑥2 та 𝑦 = −𝑥2 + 4𝑥 № 10, 2005
|
А |
Б |
В |
Г |
Д |
|
4 𝑆 =∫4𝑥𝑑𝑥 0 |
4 𝑆 =∫(−2𝑥2+4𝑥)𝑑𝑥 0 |
2 𝑆 =∫(2𝑥2−4𝑥)𝑑𝑥 0 |
2 𝑆 =∫(4𝑥−2𝑥2)𝑑𝑥 0 |
Інша відповідь |
Завдання відкритої форми з короткою відповіддю
Визначте додатне значення параметра 𝑎, за якого площа фігури, обмеженої лініями ![]() (див. рисунок), 𝑦 = 0 та 𝑥 = 𝑎, дорівнює 192 кв. од.
(див. рисунок), 𝑦 = 0 та 𝑥 = 𝑎, дорівнює 192 кв. од.
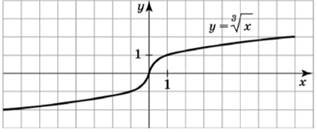
№ 36, 2015_І
Усі вершини трапеції 𝐴𝐵𝐶𝐷належать графіку функції 𝑦 = 36 − 𝑥2, побудованому в прямокутній декартовій системі координат. Більша основа 𝐴𝐷 лежить на осі 𝑥. Яку найбільшу площу може маги трапеція 𝐴𝐵𝐶𝐷? № 32, 2014д
На рисунку зображено ескіз графіка квадратичної функції ![]() . Площа криволінійної трапеції, обмеженої лініями 𝑦 = 𝑓(𝑥),𝑦 = 0, 𝑥 = 0, 𝑥 = 1, дорівнює
. Площа криволінійної трапеції, обмеженої лініями 𝑦 = 𝑓(𝑥),𝑦 = 0, 𝑥 = 0, 𝑥 = 1, дорівнює
21 кв. од. Обчисліть суму а + 𝑏 № 32, 2014
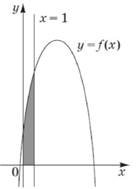
Обчисліть площу фігури, обмеженої графіком функції ![]() і прямими
і прямими
![]() № 30, 2013_ІІ
№ 30, 2013_ІІ
Обчисліть площу фігури, обмеженої лініями: ![]() .
.
№ 34, 2010_ІІ
Задано функції 𝑓(𝑥) = 𝑥2 + 1, 𝑔(𝑥) = 7 − 𝑥.
1. Знайдіть абсциси точок перетину графіків функцій 𝑓(𝑥) і 𝑔(х). У прямокутній системі координат зобразіть фігуру, обмежену цими графіками.
2. Обчисліть площу фігури, обмеженої графіками функцій 𝑓(𝑥) і 𝑔(х).
У відповідь запишіть результат, округлений до цілих № 32, 2009 Річка тече лугом і двічі перетинає шосе, утворюючи криву 𝑦 = 3𝑥 − 𝑥2. Яка площа (км2) лугу між шосе та річкою, якщо вважати, що лінія шосе збігається з віссю ОХ (див. рис)? Одиниця довжини – 1 км.
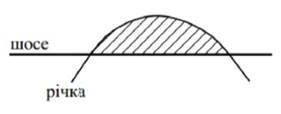 № 30, 2006
№ 30, 2006
Завдання відкритої форми з розгорнутою відповіддю
Задано функції ![]() .
.
1. Побудуйте графік функції 𝑓
2. Побудуйте графік функції 𝑔
3. Визначте абсциси точок перетину графіків функцій 𝑓 і 𝑔.
4. Обчисліть площу фігури, обмеженої графіками функцій 𝑓 і 𝑔 та віссю 𝑦.
№ 31, 2018д
|
Задано функції 𝑓(𝑥) = 𝑥3 𝑖 𝑔(𝑥) = 4|𝑥|. 1. Побудуйте графік функції 𝑓 2. Побудуйте графік функції 𝑔 3. Визначте абсциси точок перетину графіків функцій 𝑓 і 𝑔. |
|
|
4. Обчисліть площу фігури, обмеженої графіками функцій 𝑓 і 𝑔.
Задано функцію 𝑓(𝑥) = 𝑥2 − 6𝑥 + 9. |
№ 31, 2018 |
1. Визначте координати точок перетину графіка функції 𝑓 з осями координат.
2. Побудуйте графік функції 𝑓.
3. Запишіть загальний вигляд первісних для функції 𝑓.
4. Обчисліть площу фігури, обмеженої графіком функції 𝑓 та осями 𝑥 і 𝑦. № 31, 2017
КОМБІНАТОРИКА
Завдання з вибором однієї правильної відповіді
На вершину гори ведуть 5 доріг. Скільки всього є варіантів вибору маршруту підйому на вершину гори однією дорогою, а спуску – іншою? № 8, 2020
|
А |
Б |
В |
Г |
Д |
|
5 |
9 |
10 |
20 |
25 |
Блок соціальної реклами складається з 4 рекламних роликів: про шкідливість паління, про охорону навколишнього середовища, про дотримання правил дорожнього руху та про велосипедне місто. Ролик про шкідливість паління заплановано показати двічі - першим і останнім, а інші три ролики – по одному разу. Скільки всього існує варіантів формування цього блоку соціальної реклами за вказаним порядком рекламних роликів?
№ 4, 2014д
|
А |
Б |
В |
Г |
Д |
|
6 |
8 |
12 |
24 |
120 |
Студент на першому курсі повинен вибрати одну з трьох іноземних мов, яку вивчатиме, та одну з п'яти спортивних секцій, що відвідуватиме. Скільки всього існує варіантів вибору студентом іноземної мови та спортивної секції? № 6, 2014
|
А |
Б |
В |
Г |
Д |
|
5 |
8 |
10 |
15 |
28 |
|
А |
Б |
В |
Г |
Д |
Кодовий замок на дверях має десять кнопок, на яких нанесено десять різних цифр (див. рисунок). Щоб відчинити двері, потрібно одночасно натиснути дві кнопки, цифри на яких складають код замка.

Скільки всього існує різних варіантів коду замка? Уважайте, що коди, утворені перестановкою цифр (наприклад, 1-2 і 2-1), є однаковими. № 21, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
100 |
90 |
45 |
20 |
10 |
Студенти однієї з груп під час сесії повинні скласти п'ять іспитів. Заступнику декана потрібно призначити складання цих іспитів на п'ять визначених дат. Скільки всього існує різних варіантів розкладу іспитів для цієї групи? № 23, 2010_І
|
А |
Б |
В |
Г |
Д |
|
5 |
25 |
60 |
120 |
240 |
До складу української Прем'єр-ліги з футболу входять 16 команд. Упродовж сезону кожні дві команди грають між собою 2 матчі. Скільки всього матчів буде зіграно за сезон? № 18, 2009
|
120 |
128 |
200 |
240 |
256 |
Задано цифри 2;3;4;5;6. Знайдіть кількість непарних п’ятицифрових чисел, які можна скласти із цих цифр, використовуючи кожну цифру тільки один раз. № 9, 2005
|
А |
Б |
В |
Г |
Д |
|
24 |
48 |
72 |
120 |
240 |
Завдання відкритої форми з короткою відповіддю
Олег пише смс-повідомлення з трьох речень. У кінці кожного з них він прикріпить один із п’ятнадцяти веселих смайликів. Скільки всього є способів вибору таких смайликів для прикріплення, якщо всі смайлики в повідомлені мають бути різними? № 29, 2021д
Редактор стрічки новин вирішує, у якій послідовності розмістити 6 різни новин: 2 політичні, 3 суспільні й 1 спортивну. Скільки всього є різних послідовностей розміщення цих 6 новин у стрічці за умови, що політичні новини мають передувати іншим, а спортивна новина – бути останньою? Уважайте, що кожну із цих 6 новин у стрічці не повторюють. № 29, 2021
Компанія з 6 дорослих, з яких лише двоє мають відповідні посвідчення водія, сідають в автомобіль, у якому окрім місця водія є ще 5 пасажирських місць. Скільки всього є способів у цих 6 осіб зайняти місця в автомобілі, якщо на місці водія має бути особа з відповідним посвідченням? № 31, 2020д
У магазині в продажу є 6 видів тарілок, 8 видів блюдець та 12 видів чашок. Олена збирається купити бабусі в подарунок в цьому магазині або чашку та блюдце, або лише тарілку. Скільки всього є способів в Олени купити бабусі такий подарунок?
№ 29, 2019д
У фінал пісенного конкурсу вийшло 4 солісти та 3 гурти. Порядковий номер фіналістів визначають жеребкуванням. Скільки всього є варіантів послідовностей виступів фіналістів, якщо спочатку виступатимуть гурти, а після них – солісти? Уважайте, що кожен фіналіст виступатиме у фіналі лише один раз. № 29, 2019
Піцерія пропонує послугу «Зроби піцу сам», що передбачає вибір клієнтом добавок для піци. Поміж добавок – 8 м’ясних (шинка, ковбаса та інші) і 9 овочевих (цибуля, перець та інші). Клієнт вибирає 2 м’ясні добавки, однією з яких обов’язково має бути шинка, і 3 – овочевих за винятком цибулі. Скільки всього існує варіантів такого вибору добавок клієнтом? № 29, 2018д
В Оленки є 8 різних фотографій з її зображенням та 6 різних фотографій її класу. Скільки всього в неї є способів вибрати з них 3 фотографії зі своїм зображенням для персональної сторінки в соціальній мережі та 2 фотографії свого класу для сайту школи?
№ 29, 2018 У магазині в наявності є 10 видів тортів та 15 видів пачок печива. Скільки всього є способів вибору в цьому магазині або одного торта, або трьох різних пачок печива для святкового вечора? № 29, 2016д
У чайному кіоску в наявності є лише розфасований у коробки по 100 г листовий чорний чай 7 видів, серед яких є вид «Чорна перлина». Покупець вирішив придбати в цьому кіоску для подарункового набору три коробки чорного чаю трьох різних видів, серед яких обов'язково повинен бути вид «Чорна перлина». Скільки всього в покупця є варіантів такого придбання трьох коробок чаю для набору з наявних у кіоску?
№ 30, 2016
У школі є два одинадцятих класи. В 11-А класі навчається 12 хлопців та 8 дівчат, а в 11-Б – 9 хлопців та 15 дівчат. З учнів цих двох класів потрібно обрати двох ведучих для проведення святкового вечора, причому хлопець має бути з 11-А класу, а дівчина – з 11Б. Скільки всього існує варіантів вибору таких пар ведучих? № 34, 2015_І
Скільки всього різних двоцифрових чисел можна утворити з цифр 1, 5, 7 і 8 так, щоб у кожному числі всі цифри не повторювалися? № 26, 2012_ІІ
𝑚
Скільки існує різних дробів , якщо т набуває значень 1; 2 або 4, a n набуває значень 5;
𝑛
7; 11; 13 або 17? № 26, 2012_І
ЙМОВІРНІСТЬ
Завдання з вибором однієї правильної відповіді
Із гаманця, у якому лежать 5 монет номіналом по 10 копійок, 12 монет – по 25 копійок, 3 монети – по 1 гривні, беруть навмання одну монету. Обчисліть імовірність того, що її номінал буде менше 50 копійок. № 8, 2020д
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
1 |
Кожну грань кубика пофарбували або в синій, або в жовтий колір. Імовірність того, що при підкиданні кубика випаде синя грань, дорівнює ![]() . Скільки всього граней кубика пофарбували в жовтий колір? № 9, 2015_ІІ
. Скільки всього граней кубика пофарбували в жовтий колір? № 9, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
п’ять |
чотири |
три |
дві |
одну |
Випущено партію з 300 лотерейних білетів. Імовірність того, що навмання вибраний білет із цієї партії буде виграшним, дорівнює 0,2. Визначте кількість білетів без виграшу серед цих 300 білетів. № 9, 2015_І
|
А |
Б |
В |
Г |
Д |
|
6 |
60 |
294 |
150 |
240 |
На полиці знаходяться 18 однакових скляних банок із джемом. Серед них – 6 банок з абрикосовим джемом, 12 – з яблучним. За кольором джеми не відрізняються один від одного. Господиня навмання взяла одну банку. Яка ймовірність того, що вона буде з абрикосовим джемом? № 18, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Пасічник зберігає мед в однакових закритих металевих бідонах. їх у нього дванадцять: у трьох бідонах міститься квітковий мед, у чотирьох – мед із липи, у п'яти – мед із гречки. Знайдіть імовірність того, що перший навмання відкритий бідон буде містити квітковий мед. № 15, 2010_І
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
У туриста є 10 однакових за розмірами консервних банок, серед яких 4 банки –з тушкованим м’ясом, 6 банок –з рибою. Під час зливи етикетки відклеїлися. Турист навмання взяв одну банку. Яка ймовірність того, що вона буде з рибою? № 13, 2009
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30? № 3, 2007
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Власник банкоматної картки забув останні дві цифри свого PIN-коду, але пам'ятає, що вони різні. Знайдіть імовірність того, що з першої спроби він отримає доступ до системи.
№ 16, 2006
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Завдання відкритої форми з короткою відповіддю
На виборах президента школи балотується три кандидати: Наталя, Микола й Антон. За результатами опитування ймовірність того, що переможе Антон, дорівнює ймовірності того, що переможе Микола, й вдвічі менша за ймовірність того, що переможе Наталя.
Якою за результатами опитування є ймовірність того, що президентом школи оберуть
Миколу? № 25, 2021д
У першому класі 15 дівчаток, з яких лише одна на ім’я Дарина, і 11 хлопчиків. На першому уроці вчителька навмання формує пари дітей, які сидітимуть за однією партою. Першою вона вибирає пару для Дарини. Яка ймовірність того, що Дарина сидітиме за однією партою з дівчинкою? № 25, 2021
Для участі в роботі студентської ради з кожної з двох груп навмання вибирають по 1 студенту. Серед 24 студентів першої групи проживають у гуртожитку 6 студентів, а серед 28 студентів другої групи – 14 студентів. Яка ймовірність того, що обидва вибрані для роботи в раді студенти будуть з тих, хто проживає в гуртожитку? № 31, 2020
Спортсмен робить один постріл у мішень. Імовірність того, що він улучить у мішень, у 7 разів більша за імовірність того, що він у неї не влучить. Обчисліть імовірність того, що спортсмен улучить у мішень. № 29, 2017д
У торбинці лежать 3 цукерки з молочного шоколаду та m цукерок з чорного шоколаду. Усі цукерки – однакової форми й розміру. Якого найменшого значення може набувати m, якщо ймовірність навмання витягнути з торбинки цукерку з молочного шоколаду менша за 0,25? № 29, 2017
У фестивалі беруть участь 25 гуртів, серед яких є по одному гурту з України і Чехії. Порядок виступу гуртів визначається жеребкуванням, за яким кожен із гуртів має однакові шанси отримати будь-який порядковий номер від 1 до 25. Знайдіть імовірність того, що на цьому фестивалі гурт з України виступатиме першим, а порядковий номер виступу гурту з Чехії буде парним. № 31, 2013_ІІ В автобусному парку налічується n автобусів, шосту частину яких було обладнано інформаційними табло. Пізніше інформаційні табло встановили ще на 4 автобуси з наявних у парку. Після проведеного переобладнання навмання вибирають один з п автобусів парку. Ймовірність того, що це буде автобус з інформаційним табло, становить 0,25. Визначте п. Уважайте, що кожен автобус обладнується лише одним табло.
№ 29, 2013_І
У відділі працює певна кількість чоловіків і жінок. Для анкетування навмання вибрали одного із співробітників. Імовірність того, що це чоловік, дорівнює ![]() . Знайдіть відношення кількості жінок до кількості чоловіків, які працюють у цьому відділі.
. Знайдіть відношення кількості жінок до кількості чоловіків, які працюють у цьому відділі.
№ 31, 2011
У коробці є 80 цукерок, з яких 44 – з чорного шоколаду, а решта – з білого. Визначте ймовірність того, що навмання взята цукерка з коробки буде з білого шоколаду.
№ 30, 2008
СТАТИСТИКА
Завдання з вибором однієї правильної відповіді
У групі з 20 учнів 11 класу провели анкетування, щоб з’ясувати, скільки приблизно годин на день кожен з них користується Інтернетом. Відповіді учнів відображено на діаграмі (див. рисунок). Визначте, скільки часу на день (у год) у середньому учень з цієї групи користується Інтернетом. № 11, 2018д
|
А |
Б |
В |
Г |
Д |
|
2,9 |
2,5 |
2 |
3 |
3,2 |
Учень з понеділка до п’ятниці записував час (у хвилинах), який він витрачав на дорогу до школи та зі школи (див. таблицю).
 Дорога Дні понеділок вівторок середа четвер п’ятниця до школи 19 20 21 17 23 зі школи 28 22 20 25 30
Дорога Дні понеділок вівторок середа четвер п’ятниця до школи 19 20 21 17 23 зі школи 28 22 20 25 30
На скільки хвилин у середньому дорога зі школи триваліша за дорогу до школи?
№ 12, 2018
|
А |
Б |
В |
Г |
Д |
|
2 |
3 |
4 |
5 |
6 |
О шостій годині ранку визначено температуру на десяти метеостанціях. Отримані дані відображено в таблиці.
|
Температура (у градусах) |
1 |
3 |
4 |
х |
|
Кількість метеостанцій |
2 |
3 |
4 |
1 |
Визначте х, якщо середнє арифметичне всіх цих даних дорівнює 3,5°. № 20, 2011
|
А |
Б |
В |
Г |
Д |
|
5 |
6 |
7 |
8 |
9 |
В уривку із художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода – це те значення випадкової величини, яке зустрічається найчастіше) цього розподілу за допомогою зображеного на рисунку полігона частот. № 6, 2008
|
А |
Б |
В |
Г |
Д |
|
2 |
4 |
5 |
8 |
10 |
Завдання на встановлення відповідності
У шкільній олімпіаді з географії взяли участь 20 учнів десятих класів. Бали, набрані учасниками олімпіади, утворили певний ряд даних, на основі якого склали його статистичний розподіл частот:
|
Бал |
5 |
7 |
9 |
10 |
12 |
15 |
16 |
18 |
|
Частота бала |
3 |
4 |
2 |
1 |
5 |
3 |
1 |
1 |
За цим статистичним розподілом частот установіть відповідність між характеристикою ряду даних (1–4) та її числовим значенням (А–Д). № 24, 2014д
|
Характеристика ряду даних |
Числове значення характеристики |
|
1 розмах |
А 10,5 |
|
2 мода |
Б 11 |
|
3 медіана |
В 11,5 |
|
4 середнє значення |
Г 12 |
|
|
Д 13 |
На рисунку зображено полігон частот певного ряду даних, на якому по осі абсцис відмічені елементи цього ряду, а по осі ординат – їхні частоти. Установіть відповідність між характеристикою (1–4) цього ряду даних та її числовим значенням (А–Д).
|
|
№ 24, 2014 |
|
Характеристика ряду даних |
Числове значення характеристики |
|
1 кількість елементів |
А 12 |
|
2 розмах |
Б 18 |
|
3 мода |
В 21 |
|
4 медіана |
Г 30 |
|
|
Д 36 |
Завдання відкритої форми з короткою відповіддю
У таблиці відображено інформацію про ціну та кількість зошитів, придбаних за цією ціною Олексієм. За даними таблиці визначте середню ціну (у грн) одного зошита з придбаних Олексієм.
|
Ціна одного зошита, грн |
8 |
10 |
12 |
|
Кількість зошитів |
9 |
4 |
7 |
№ 29, 2020д
У першому рядку таблиці наведено значення температури повітря, яку вимірювали на метеостанції через кожні 3 години впродовж доби. У другому рядку зазначено частоту фіксувань відповідного значення температури впродовж доби. За даними метеостанції визначте середню температуру ( у 0С) протягом цієї доби.
|
Температура,0 С |
12 |
15 |
17 |
18 |
|
Частота фіксувань |
1 |
4 |
2 |
1 |
№ 29, 2020
Середній вік одинадцяти футболістів команди становить 22 роки. Під час гри одного з футболістів було вилучено з поля, після чого середній вік гравців, що залишилися, став
21 рік. Скільки років футболісту, який залишив поле? № 28, 2007
ГРАФІКИ І ДІАГРАМИ
Завдання з вибором однієї правильної відповіді
Кілкість відвідувачів ботанічного саду протягом червня становила чверть від їх сумарної кількості в травні й червні. На якій із діаграм правильно зображено розподіл відвідувачів цього ботанічного саду впродовж цих двох місяців?
![]() – кількість відвідувачів у травні
– кількість відвідувачів у травні
– кількість відвідувачів у червні № 2, 2021д
На графіку відображено зміну робочої температури двигуна легкового автомобіля протягом 10 хвилин з моменту його запуску. Визначте за графіком кількість хвилин, протягом яких робоча температура двигуна була не більшою за 500С. № 2, 2021
|
А |
Б |
В |
Г |
|
7 |
4 |
3 |
2 |
На діаграмі відображено інформацію про кількість відвідувачів кінотеатру на кожному з шести сеансів. Укажіть усі сеанси, на яких відвідувачів було не менше ніж 170 осіб.
№ 9, 2019д
|
А |
Б |
В |
Г |
Д |
|
III, IV, V, VI |
III, V, VI |
I, II, IV |
III, V |
I, II |
На діаграмі відображено розподіл кількості працівників фірми за віком. Скільки всього працює працівників на цій фірмі. № 11, 2019
|
А |
Б |
В |
Г |
Д |
|
40 |
96 |
120 |
144 |
110 |
У таблиці наведено дані про температуру повітря в різний час того самого дня.
|
Час, години |
6 |
9 |
12 |
15 |
18 |
|
Температура, 0С |
12 |
17 |
14 |
18 |
15 |
На графіках немає шкали (градації) температури повітря. На якому графіку правильно відображені дані, наведені в таблиці? № 5, 2017д
У таблиці наведено дані про кількість глядачів, які відвідали кінотеатр протягом п’яти днів тижня
|
День тижня |
понеділок |
вівторок |
середа |
четвер |
п’ятниця |
|
Кількість відвідувачів |
82 |
116 |
102 |
140 |
130 |
На діаграмах немає шкали (градації) кількості глядачів. Визначте, на якій діаграмі правильно відображено дані, наведені в таблиці. № 4, 2017
На діаграмі відображено обсяг видобутку алмазів (у млн карат) у 2006 році в п'яти країнах Африки. Користуючись діаграмою, визначте країни Африки, у кожній з яких маса алмазів, видобутих у 2006 році, більш ніж удвічі перевищувала масу алмазів, видобутих у цьому році в Анголі. № 7, 2016д
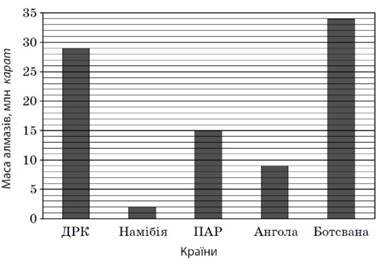
|
А |
Б |
В |
Г |
Д |
|
лише в ДРК |
лише в ПАР і ДРК |
лише в Ботсвані |
лише в ПАР у ДРК і в Ботсвані |
лише в ДРК і в Ботсвані |
На рисунку жирними точками позначено річні мінімуми площі поверхні арктичного льоду, що спостерігалися з 2004 р. до 2014 р. (для наочності точки з'єднано відрізками). По горизонталі відмічено роки, а по вертикалі – площу поверхні льоду (у млн км ). Користуючись наведеною інформацією, визначте із зазначеного періоду рік, у якому величина річного мінімуму площі поверхні льоду змінилась найбільше порівняно з попереднім роком. № 7, 2016
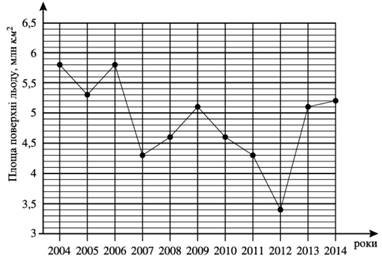
|
А |
Б |
В |
Г |
Д |
|
2006 |
2007 |
2009 |
2012 |
2013 |
Діаграма, зображена на рисунку, містить інформацію про кількість електроенергії (у кВт · год), спожитої певною сім'єю в кожному місяці 2012 року. Користуючись діаграмою, установіть, які з наведених тверджень є правильними.
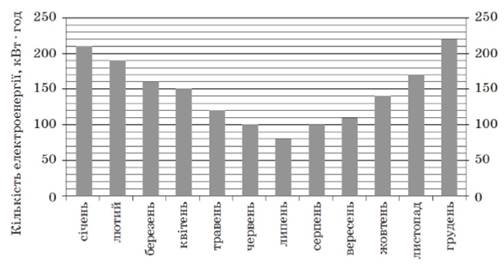
I. У грудні порівняно з липнем спожито електроенергії більше, ніж у 2 рази.
II. За всі літні місяці спожито електроенергії на 150 кВт · год менше, ніж за всі весняні місяці.
III. Середньомісячне споживання електроенергії за рік є більшим за 120 кВт · год.
№ 2, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
лише І |
лише І і ІІ |
лише І і ІІІ |
лише ІІ і ІІІ |
І, ІІ і ІІІ |
На діаграмі відображено нараховану фірмою загальну суму заробітної плати усім своїм працівникам у січні, лютому та березні 2011 року. У січні на фірмі працювали 15 співробітників, у лютому – 18, а в березні – 25. № 10, 2013_І
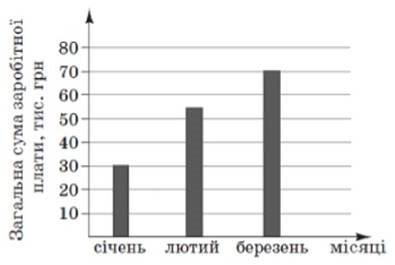
Як змінилася середня нарахована заробітна плата в цій фірмі в березні порівняно з січнем?
|
А |
зменшилась більше ніж на 1000 грн |
|
Б |
зменшилась менше ніж на 1000 грн |
|
В |
не змінилась |
|
Г |
збільшилась менше ніж на 1000 грн |
|
Д |
збільшилась більше ніж на 1000 грн |
На рисунку показано жирними точками найвищу і найнижчу температури повітря кожного дня тижня з понеділка до п'ятниці в деякому місті України. По горизонталі відмічено дні тижня, а по вертикалі – температуру повітря в градусах Цельсія. У який день різниця між найвищою та найнижчою температурами повітря була найбільшою?
№ 1, 2012_ІІ

|
А |
Б |
В |
Г |
Д |
|
понеділок |
вівторок |
середа |
четвер |
п’ятниця |
На діаграмі відображено кількість відвідувачів Музею води протягом одного робочого тижня (з вівторка до неділі). У який день тижня кількість відвідувачів була вдвічі більшою, ніжу попередній день? № 3, 2012_І
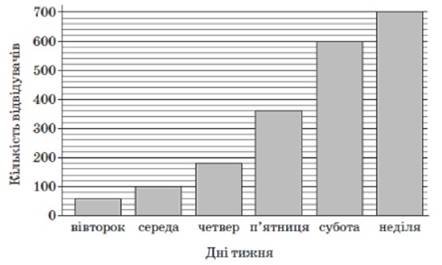
|
А |
Б |
В |
Г |
Д |
|
середа |
четвер |
п’ятниця |
субота |
неділя |
Діаграма, зображена на рисунку, містить інформацію про кількість опадів (у мм), що випали упродовж року в місті N. Користуючись діаграмою, установіть, які з наведених тверджень є правильними.
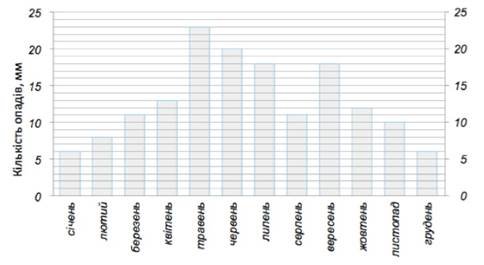
I. Улітку опадів випало менше, ніж навесні.
II. У вересні опадів випало у 1,5 рази більше, ніж у жовтні.
III. Середня місячна кількість опадів за рік становить 19 мм.
№ 14, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
лише І |
лише ІІ |
лише І і ІІ |
лише ІІ і ІІІ |
лише І і ІІІ |
У саду ростуть 60 дерев: 28 яблунь, 20 вишень і 12 абрикос. На одній із діаграм правильно зображено розподіл дерев у саду. Укажіть цю діаграму. № 11, 2010_І
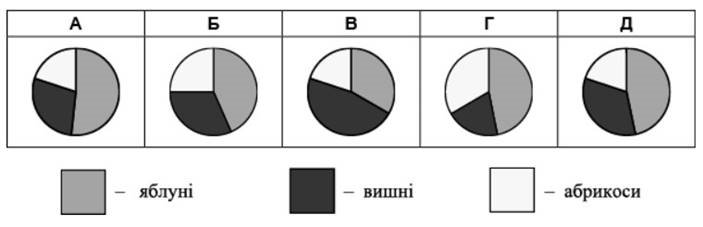
Під час закладання нового парку 25% його площі відвели під посадку кленів, 50% площі, що залишилася, – під посадку дубів, а решту площі – під газони. Вкажіть, на якій із діаграм правильно показано розподіл посадок. № 3, 2008

ВІДСОТКИ
Завдання з вибором однієї правильної відповіді
Журнал коштував 25 грн. Через два місяці цей самий журнал став коштувати 21 грн. На скільки відсотків знизилася ціна журналу? № 8, 2011
|
А |
Б |
В |
Г |
Д |
|
4% |
|
|
84% |
16% |
Перед Новим роком у магазині побутової техніки на всі товари було знижено ціни на 15%. Скільки коштуватиме після знижки телевізор вартістю 1800 грн? № 3, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
1200 грн |
1350 грн |
1430 грн |
1530 грн |
1785 грн |
За видачу свідоцтва про право на спадщину стягується державне мито в розмірі 0,5% від вартості майна, що успадковується. Скільки державного мита повинен сплатити спадкоємець, якщо вартість майна, що успадковується, становить 32000 грн?
№ 3, 2010_І
|
А |
Б |
В |
Г |
Д |
|
16 грн |
64 грн |
160 грн |
320 грн |
1600 грн |
За переказ грошей клієнт повинен сплатити банку винагороду в розмірі 2% від суми переказу. Скільки всього грошей (у гривнях) йому потрібно сплатити в касу банку, якщо сума переказу становить 30000 грн? № 8, 2009
|
А |
Б |
В |
Г |
Д |
|
36000 грн |
30600 грн |
30060 грн |
30030 грн |
30006 грн |
Банк сплачує своїм вкладникам 8% річних. Визначте, скільки грошей треба покласти на рахунок, щоб через рік отримати 60 грн. прибутку. № 2, 2007
|
А |
Б |
В |
Г |
Д |
|
1150 |
1050 |
950 |
850 |
750 |
Товар подешевшав на 20 %. На скільки відсотків більше можна купити товару за ту ж саму суму грошей? № 6, 2006
|
А |
Б |
В |
Г |
Д |
|
|
|
10% |
20% |
25% |
У банку відкрили рахунок на 1000 грн. під 20 % річних. Наприкінці кожного з перших двох років зберігання грошей у банку після нарахування відсотків, вкладник додатково вносив ще 𝑎 грн. На кінець третього року виявилось, що розмір вкладу збільшився у порівнянні з початковим вкладом на 300 %. Яке з рівнянь відповідає умові задачі?
№ 8, 2005
|
А |
((1000 ∙ 1,2 + 𝑎) ∙ 1,2 + 𝑎) ∙ 1,2 = 1000 ∙ 4 |
|
Б |
((1000 ∙ 0,2 + 𝑎) ∙ 0,2 + 𝑎) ∙ 0,2 = 1000 ∙ 4 |
|
В |
((1000 ∙ 1,2 + 𝑎) ∙ 1,2 + 𝑎) ∙ 1,2 = 1000 ∙ 3 |
|
Г |
((1000 ∙ 0,2 + 𝑎) ∙ 0,2 + 𝑎) ∙ 0,2 = 1000 ∙ 3 |
|
Д |
(1000 ∙ 1,2 + 𝑎) ∙ 2 = 1000 ∙ 3 |
Завдання відкритої форми з короткою відповіддю
На пачці морозива масою 500 г наведено інформацію (див. рисунок) про поживну (харчову) цінність цього продукту масою 100 г: білків – 3,5 г, жирів – 12 г, вуглеводів – 21 г.

1. Визначте енергетичну (калорійну) цінність (у ккал) цього морозива масою 100 г, якщо енергетична цінність білків масою 1 г становить 4 ккал, жирів масою 1 г – 9 ккал, вуглеводів масою 1 г – 4 ккал.
2. Морозиво, з’їдене Ладою, становить 30% від усієї пачки (500 г). Визначте енергетичну цінність (у ккал) спожитого нею морозива. № 21, 2021д
Олена купила через веб-сайт посадочний документ (див. фрагмент документа) на потяг, що коштує 240 грн. У його вартість входять вартості: квитка – 34,50 грн, плацкарти – 147 грн й інших витрат – 58,50 грн. За 10 годин до відправлення потяга Олена вирішила повернути цей посадочний документ. Відповідно до правил за таких умов їй повертають лише вартість квитка й половину вартості плацкарти. Крім того, за повернення посадочного документа з Олени додатково стягують збір 18 грн.

1. Яку суму грошей 𝑃 (у грн) отримає Олена, повернувши цей документ?
2. Скільки відсотків від вартості документа становить сума грошей 𝑃?
№ 21, 2021
Михайло планував купити мобільний телефон, чохол до нього та карту пам’яті. Вартість телефона становить 4500 грн, чохла – 200 грн, карти пам’яті – 300 грн. У магазині проходить акція: купивши телефон, покупець отримує карту пам’яті в подарунок, а на чохол йому нададуть знижку розміром п’ятої частини від його вартості.
1. Яку суму грошей 𝑃 (у грн) заплатить Михайло за вибраний ним телефон, чохол та карту пам’яті, якщо скористається цією акцією?
2. Скільки відсотків становить сума грошей 𝑃 від суми грошей, яку заплатив би Михайло, якби купував всі три вибрані ним товари не за акційними умовами?
№ 25, 2020д
Вартість оренди автомобіля бюджетного класу складається з основної плати та додаткової плати за понаднормовий пробіг. За перевищення норми пробігу (50 км за одну добу) нараховують додаткову плату в розмірі 6 грн за кожен понаднормовий кілометр. Пробіг автомобіля, орендованого на 6 діб, становить 420 км.
1. Яку суму грошей 𝑃 (у грн) становитиме додаткова плата за понаднормовий пробіг орендованого автомобіля?
2. Основна плата за оренду автомобіля є фіксованою й становить 400 грн за кожну добу. Скільки відсотків від основної плати за 6 діб становить сума грошей 𝑃?
№ 25, 2020
У дитячому шаховому клубі функціонують лише молодша й старша групи. Старшу групу відвідують 27 дітей. Відвідувачі молодшої групи становлять 46% від загальної кількості відвідувачів обох груп шахового клубу. 1. Визначте кількість дітей у молодшій групі.
2. Скільки дітей потрібно додатково набрати в молодшу групу за умови незмінності кількості дітей старшої групи, щоб відношення кількості відвідувачів молодшої групи до кількості відвідувачів старшої групи становило 4:3? № 25, 2019д
У таблиці наведено тарифи на доставку вантажу за маршрутом N службою кур’єрської доставки. Будь-яку кількість вантажів можна об’єднувати в один, маса якого дорівнює сумі мас об’єднаних вантажів. Жодних додаткових платежів за об’єднання вантажів чи доставку вантажу, окрім указаних у таблиці немає.
|
Маса вантажу, кг |
Вартість доставки вантажу, грн |
|
до 50 |
100 |
|
51-75 |
110 |
|
76-100 |
205 |
|
101-150 |
310 |
1. За яку найменшу суму P (у грн) можна доставити цією службою за маршрутом N три вантажі, маси яких становлять 31 кг, 36 кг та 40 кг?
2. Скільки відсотків становить P від загальної суми грошей за доставку цих трьох вантажів, якщо кожен з них відправляти окремо? № 25, 2019
На клумбі висадили рядами 125 кущів троянд з однаковою кількістю кущів у кожному ряду. Виявилося, що кількість рядів на 20 менша за кількість кущів у кожному ряду.
1. Скільки висадили кущів троянд у кожному ряду?
2. Узимку в першому ряду зазнали ушкоджень 16% кущів троянд. Скільки кущів троянд у першому ряду перезимували неушкодженими? № 25, 2018д
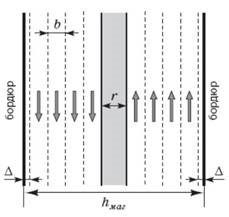 Для визначення ширини автомагістралі ℎмаг (у м), що має по 4 однакових смуги руху транспорту в обох напрямках
Для визначення ширини автомагістралі ℎмаг (у м), що має по 4 однакових смуги руху транспорту в обох напрямках
(див. рисунок), використовують формулу ℎмаг = 8𝑏 + 𝑟 +
2∆, де
b – ширина однієї смуги руху транспорту;
r – ширина розділювальної смуги між напрямками руху транспорту;
Δ – ширина запобіжної смуги між крайньою смугою руху й бордюром.
1. Визначте ширину b (у м) однієї смуги, якщо ℎмаг = 40,2м, r = 10м, Δ = 1,5м.
2. Заплановано збільшити ширину b кожної смуги руху транспорту на 10% за рахунок зменшення лише зменшення ширини r розділювальної смуги. На скільки метрів потрібно зменшити ширину r розділювальної смуги? № 25, 2018
Для поповнення рахунку телефону Андрій вніс певну суму грошей до платіжного терміналу. З цієї суми утримано комісійний платіж у розмірі 2грн 40 коп., що становить 3% від суми, внесеної до терміналу. У результаті рахунок телефону поповнено на решту внесеної суми.
1. Яку суму грошей (у грн.) Андрій вніс до платіжного терміналу?
2. Мобільний оператор, послугами якого користується Андрій, нараховує 8 бонусів за кожні 5 грн., на які поповнено рахунок телефону. На залишок грошей, менший за 5 грн., бонуси не нараховуються. Скільки бонусів нараховано Андрію за здійснене ним поповнення рахунку телефону? № 25, 2017
Для 80 учнів 9-х класів вирішена закупити зошити в клітинку та в лінійку для контрольних робіт. Кожному учневі потрібно 9 зошитів у клітинку, а в лінійку – у три рази менше. Вартість одного зошита (у клітинку або в лінійку) становить 3 гри. При купівлі зошитів в упаковках по 10 штук у кожній надається знижка 5%.
1. Визначте загальну кількість N зошитів у клітинку та в лінійку, які потрібно закупити для 80 учнів.
2. Скільки гривенъ коштуватимуть усі N зошитів, якщо купувати їх в упаковках по 10 штук (з урахуванням знижки)?
Відповідь надайте у вигляді двох чисел, розділених крапкою з комою.
№ 25, 2016д
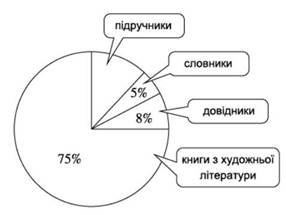 У бібліотеці є лише підручники, словники, довідники та художня література.Відсотковий розподіл кількості цих книг у бібліотеці відображено на діаграмі.
У бібліотеці є лише підручники, словники, довідники та художня література.Відсотковий розподіл кількості цих книг у бібліотеці відображено на діаграмі.
1. Визначте загальну кількість книг у цій бібліотеці, якщо кількість підручників дорівнює 72.
2. Скільки потрібно придбати додатково підручників, щоб отримана після цього їх сумарна кількість відносилася до кількості довідників як 4:1. Відповідь надайте у вигляді двох чисел, розділених крапкою з комою.
Відповідь надайте у вигляді двох чисел, розділених крапкою з комою.
№ 25, 2016
Мобільний телефон у магазині коштує 2260 грн. Покупець не має можливості заплатити всю суму повністю, тому купує цей телефон у розстрочку. За умовами договору він має сплачувати 10% від його ціни кожен місяць протягом 12 місяців з моменту купівлі.
1. Визначити щомісячний платіж за куплений у розстрочку телефон (у грн.)
2. Знайдіть суму 12 щомісячних платежів. На скільки гривень ця сума перевищує заявлену магазином ціну телефону (2260 грн) на момент купівлі?
№ 25, 26, 2015_ІІ
У магазині в продажу є лише музичні диски, диски з науково-популярними фільмами та диски з художніми фільмами. Кількість дисків із науково-популярними фільмами в п'ять разів більша за кількість музичних дисків і вдвічі менша за кількість дисків із художніми фільмами. Загальна кількість дисків у цьому магазині дорівнює 192.
1. Скільки відсотків становить кількість музичних дисків від загальної кількості всіх дисків у магазині?
2. Визначте кількість дисків із науково-популярними фільмами в цьому магазині.
№ 25, 26, 2015_І
Визначте вартість (у грн) спожитої за місяць користувачем пільгової категорії електроенергії (див. фрагмент квитанції).
|
Пільга (%), ліміт (кВт год) 25% при нормі 75 кВт·год |
|
|||
|
Поточні показання, кВт·год |
Попередні показання, кВт·год |
Спожито, кВт·год |
Тариф, грн |
Сума до сплати, грн |
|
6275 |
6160 |
115 |
0,28 |
? |
Урахуйте те, що тариф (вартість однієї кВт·год) становить 0,28 грн. Надана цьому користувачеві пільга полягає в тому, що за 75 кВт·год зі спожитих за місяць користувач сплачує на 25% менше від їхньої вартості за тарифом.
№ 27, 2014д
Початкова вартість сукні становила 144 грн. Унаслідок уцінення вартість цієї сукні було зменшено на 60%.
1. Обчисліть вартість сукні після уцінення (у грн).
2. Скільки відсотків становить початкова вартість сукні від її вартості після уцінення? Відповідь надайте у вигляді двох чисел, розділених крапкою з комою.
№ 25, 2014
У магазині молодіжного одягу діє акція: при покупці будь-яких двох однакових футболок за одну з них платять на 40% менше, ніж за іншу. За дві однакові футболки, придбані в цьому магазині під час акції, Микола заплатив 200 гривень. Скільки гривень заплатить Микола, якщо він купить лише одну таку футболку? № 25, 2013_ІІ
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 6
Додатне число А більше додатного числа В у 3,8 раза. На скільки відсотків число А більше за число В? № 25, 2013_І
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
МОДУЛЬ
Завдання з вибором однієї правильної відповіді
![]()
|1 − √3| = № 15, 2020д
|
А |
Б |
В |
Г |
Д |
|
−1 − √3 |
√3 − 1 |
1 − √3 |
1 + √3 |
1 |
Якщо 𝑎 < 1, то |𝑎 − 1| + |−7| = № 17, 2017д
|
А |
Б |
В |
Г |
Д |
|
а – 8 |
а + 6 |
–а + 6 |
–а – 6 |
–а + 8 |
Якщо 𝑎 < 2, то 1 + |𝑎 − 2| =. № 18, 2017
|
А |
Б |
|
В |
|
Г |
|
Д |
|
–a – 3 |
|
–a – 1 |
|
a – 1 |
|
a + 3 |
3 – a |
Якщо ![]() № 15, 2014
№ 15, 2014
|
А |
Б |
В |
Г |
Д |
|
7 – a |
a + 7 |
a – 7 |
0 |
–7 – a |
Якщо ![]() № 19, 2012_ІІ
№ 19, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
−𝑎 − 3 |
−𝑎 − 1 |
𝑎 − 1 |
𝑎 + 3 |
−𝑎 − 3 |
Укажіть множину всіх значень 𝑎, при яких виконується рівність |𝑎3 − 𝑎2| = 𝑎3 − 𝑎2
№ 19, 2012_І
|
А |
Б |
В |
Г |
Д |
|
[1; +∞) |
{0}∪[1;+∞) |
(–∞; –1]∪{0} |
[0; 1] |
(–∞; –1]∪[1; +∞) |
Спростіть вираз 𝑎 − |𝑎|, якщо а < 0 № 11, 2011
|
А |
Б |
В |
Г |
Д |
|
2а |
а |
0 |
–а |
–2а |
СТЕПІНЬ
Завдання з вибором однієї правильної відповіді
Обчисліть ![]() № 12, 2021
№ 12, 2021
|
А |
Б |
|
Г |
Д |
|
|
|
|
|
10 |
1 −2
( ) = № 1, 2020
3
|
А |
|
Б |
В |
Г |
Д |
|
|
−9 |
|
|
|
|
9 |
|
|
= 3 то 4𝑎+1 = |
|
|
|
|
№ |
|
|
А |
|
Б |
В |
Г |
Д |
|
|
12 |
|
13 |
18 |
36 |
64 |
|
Якщо 2𝑎14, 2018д
|
|
|
|
10𝑎𝑏3 Скоротіть дріб 2𝑏 5𝑎 |
№ 1, 2017д |
|
А |
Б |
В |
Г |
Д |
|
2𝑏2
𝑎 |
|
50𝑎3𝑏4 |
|
|
|
= |
|
|
|
|
|
А |
Б |
В |
Г |
Д |
|
2𝑥5 |
20𝑥5 |
2𝑥6 |
0,2𝑥5 |
0,2𝑥6 |
0,4𝑥2 ∙ 5𝑥3№ 1, 2016
Обчисліть ![]() № 5, 2013_І
№ 5, 2013_І
|
А |
Б |
В |
Г |
Д |
|
101,5 |
102 |
108 |
109 |
1010 |
Запишіть числа 215, 410, 105 у порядку зростання № 18, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
215, 410, 105 |
215, 105, 410 |
105, 215, 410 |
105, 410, 215 |
410, 215, 105 |
Спростіть вираз 0,8𝑏9: 8𝑏3 № 3, 2011
|
А |
Б |
В |
Г |
Д |
|
0,1𝑏6 |
10𝑏6 |
6,4𝑏12 |
0,1𝑏3 |
10𝑏3 |
Спростіть вираз (𝑎6)4: 𝑎2, де 𝑎 ≠ 0 № 5, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
a5 |
a8 |
a10 |
a12 |
a22 |
𝑏2∙𝑏10
Спростіть вираз ![]() 4 , де 𝑏 ≠ 0 № 5, 2010_І
4 , де 𝑏 ≠ 0 № 5, 2010_І
𝑏
|
А |
Б |
В |
Г |
Д |
|
b16 |
b8 |
b5 |
b4 |
b3 |
Завдання на встановлення відповідності
Установіть відповідність між виразом (1–3) і твердженням про його значення (А–Д), яке є правильним, якщо ![]() . № 18, 2021
. № 18, 2021
Вираз Твердження про значення виразу
1 𝑎2 А більше від 5
2 𝑎 + |𝑎| Б належить проміжку (0; 1)
3 log5 5𝑎 В є від’ємним числом
Г належить проміжку [1; 5)
Д дорівнює 0
Установіть відповідність між виразом (1–3) та тотожно рівним йому виразом (А–Д), якщо 𝑎 – довільне додатне число, 𝑎 ≠ 1. № 22, 2020д
Вираз Тотожно рівний вираз
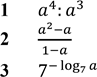 А 𝑎2
А 𝑎2
Б 𝑎7
В ![]()
Г 𝑎 Д −𝑎
Установіть відповідність між виразом (1–3) та тотожно рівним йому виразом (А–Д), якщо 𝑎 – довільне від’ємне число. № 22, 2020 Вираз Тотожно рівний вираз
1 𝑎0 А 0 2 |𝑎| + 𝑎 Б 2𝑎 3 𝑎 log2 2𝑎 В 𝑎2 Г 1 Д −2𝑎
Установіть відповідність між виразом (1–4) та тотожно рівним йому виразом (А–Д), якщо 𝑎 – довільне додатне число. № 22, 2019д
Вираз Тотожно рівний вираз
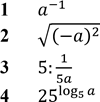 А
А ![]()
Б
𝑎
В 𝑎
Г 𝑎2
Д 25𝑎
Нехай 𝑎 довільне додатне число. Установіть відповідність між виразом (1–4) та тотожно рівним йому виразом (А – Д). № 22, 2018д Вираз Тотожно рівний вираз
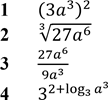 А 9𝑎6
А 9𝑎6
Б 9𝑎3
В 9𝑎5
Г 3𝑎3 Д 3𝑎2
До кожного початку речення (1–4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження, якщо а = –3. № 22, 2018
Початок речення Закінчення речення
1 Значення виразу 𝑎0 А більше за 1
2 Значення виразу 𝑎2 Б дорівнює 1
3 Значення виразу ![]() В дорівнює 0
В дорівнює 0
4 Значення виразу ![]() Г дорівнює –1
Г дорівнює –1
Д менше за –1
Нехай m i n – довільні дійсні числа, а – довільне додатне число, а ≠ 1. До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося правильне
твердження. № 22, 2017
Початок речення Закінчення речення
1 Якщо (𝑎𝑚)𝑛 = 𝑎4, то А 𝑚 + 𝑛 = 4
2 Якщо 𝑎𝑚 ∙ 𝑎𝑛 = 𝑎4, то Б 𝑚 − 𝑛 = 4
3 Якщо ![]() , то В 𝑚𝑛 = 4
, то В 𝑚𝑛 = 4
4 Якщо ![]() , то Г 𝑚 = 4𝑛
, то Г 𝑚 = 4𝑛
Д 𝑚 = 8𝑛
Установіть відповідність між числовим виразом (1–4) та проміжком (А–Д) якому
|
належить його значення. |
|
№ 22, 2016д |
|
Вираз |
Проміжок |
|
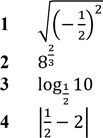 А (–∞; –3)
А (–∞; –3)
Б [–3; 0)
В [0; 1)
Г [1; 3)
Д [3; +∞)
До кожного початку речення (1–4), де а > 0, b > 0, доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження. № 21, 2014д
Початок речення Закінчення речення
|
1 |
Якщо log2 𝑎 = 2 log2 𝑏, то |
А |
𝑎 = 2𝑏 |
|
|
|
2 |
Якщо 𝑎3 = 8𝑏3, то |
Б |
𝑎 = 2 + 𝑏 |
|
|
|
3 |
Якщо |
В |
𝑎 = 4𝑏 |
|
|
|
4 |
Якщо 2𝑎 = 4 ∙ 2𝑏, то |
Г |
𝑎 = 𝑏2 |
||
|
|
|
Д |
𝑎 = 2 + 𝑏2 |
||
До кожного виразу (1–4) при a > 0 доберіть тотожно йому рівний (А–Д).
№ 21, 2012_І
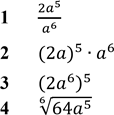 А 32𝑎11
А 32𝑎11
Б ![]()
В ![]()
Г 2𝑎−1
Д 32𝑎30
Завдання відкритої форми з короткою відповіддю
Обчисліть ![]() № 21, 2009
№ 21, 2009
![]() 83
83
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 1
КОРІНЬ
Завдання з вибором однієї правильної відповіді
![]()
Скільки всього цілих чисел містить інтервал (√8; √81)? № 17, 2020
|
А |
Б |
В |
Г |
Д |
|
8 |
7 |
6 |
5 |
4 |
![]() Якому проміжку належить значення виразу −1+√27? № 15, 2019д
Якому проміжку належить значення виразу −1+√27? № 15, 2019д
2
|
А |
Б |
В |
Г |
Д |
|
(–∞; 0) |
[0; 1) |
[1; 2) |
[2; 3) |
[3; +∞) |
3 ![]()
Якому проміжку належить число √18? № 9, 2016
|
А |
Б |
В |
Г |
Д |
|
[0; 1) |
[1; 2) |
[2; 3) |
[3; 4) |
[4; +∞) |
![]() √(−2)2 + 3√(−3)3 = № 9, 2014д
√(−2)2 + 3√(−3)3 = № 9, 2014д
|
А |
Б |
В |
Г |
Д |
|
–23 |
–5 |
–1 |
1 |
5 |
|
А |
Б |
В |
Г |
Д |
![]() 3
3
Спростіть вираз №7, 2014
|
А |
Б |
В |
Г |
Д |
|
|
|
|
4 |
16 |
Запишіть числа ![]() в порядку зростання № 8, 2012_І
в порядку зростання № 8, 2012_І
|
А |
Б |
В |
Г |
Д |
|
1, 3√2, 5√3 |
1, 5√3, 3√2 |
3 5 √2, √3, 1 |
5 3 √3,1, √2 |
3 5 √2,1, √3 |
![]()
![]()
![]()
![]() Серед чисел 𝑎 = √5 − 2, 𝑏 = 2√3 − 3√2, 𝑐 = 3√3 − 3√2 вкажіть усі додатні № 11, 2010_ІІ
Серед чисел 𝑎 = √5 − 2, 𝑏 = 2√3 − 3√2, 𝑐 = 3√3 − 3√2 вкажіть усі додатні № 11, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
a |
c |
a; b |
a; c |
a; b; c |
4 ![]()
Якому з наведених проміжків належить число √30 № 19, 2010_І
|
А |
Б |
В |
Г |
Д |
|
(1; 2) |
(2; 3) |
(3; 4) |
(4; 5) |
(5; 6) |
3
![]() Обчисліть √3128 № 3, 2009
Обчисліть √3128 № 3, 2009
√2
|
А |
Б |
В |
Г |
Д |
|
64 |
18 |
8 |
4 |
2 |
𝐺𝑀𝑚
Якщо 𝐹 = ![]() 𝑅2 𝑖 𝑅 > 0, 𝑅 = № 5, 2008
𝑅2 𝑖 𝑅 > 0, 𝑅 = № 5, 2008
Для всіх хто хоче знати математику https://terletskyi.blogspot.com/ 2
|
√𝐹𝐺𝑀𝑚 |
𝑀𝑚 √ 𝐹𝐺 |
𝐹𝐺 √ 𝑀𝑚 |
𝐹 √ |
𝐺𝑀𝑚 √ 𝐹 |
![]()
Укажіть правильну нерівність, якщо 𝑎 = 5√2, 𝑏 = 7, 𝑐 = √51 № 7, 2008
|
А |
Б |
В |
Г |
Д |
|
b < a < c |
a < b < c |
c < a < b |
a < c < b |
b < c < a |
Розташуйте у порядку спадання числа ![]() № 1, 2007
№ 1, 2007
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
1
![]() Обчисліть √1255√32 − 52 № 1, 2006
Обчисліть √1255√32 − 52 № 1, 2006
|
А |
Б |
В |
Г |
Д |
|
11√5 |
10√2 − √5 |
9 |
9√5 |
10 √4000 − √5 |
2
Обчисліть ![]() № 1, 2005
№ 1, 2005
|
А |
Б |
В |
Г |
Д |
|
0 |
2 |
2√5 |
4 |
6 |
Завдання відкритої форми з короткою відповіддю
Обчисліть значення виразу ![]() № 27, 2021
№ 27, 2021
Обчисліть значення виразу ![]() № 29, 2011
№ 29, 2011
![]() Обчисліть (6√27 + 4√64)(6√27 − 4√64) № 21, 2007
Обчисліть (6√27 + 4√64)(6√27 − 4√64) № 21, 2007
Обчисліть значення виразу ![]() № 23, 2006
№ 23, 2006
ЛОГАРИФМ. ПЕРЕТВОРЕННЯ ЛОГАРИФМІЧНИХ ВИРАЗІВ
Завдання з вибором однієї правильної відповіді
Укажіть правильну подвійну нерівність, якщо ![]()
№ 12, 2021д
|
А |
Б |
В |
Г |
Д |
|
𝑐 < 𝑏 < 𝑎 |
𝑏 < 𝑐 < 𝑎 |
𝑎 < 𝑐 < 𝑏 |
𝑐 < 𝑎 < 𝑏 |
𝑏 < 𝑎 < 𝑐 |
Якому з наведених проміжків належить число ![]() № 14, 2019
№ 14, 2019
|
А |
Б |
В |
Г |
Д |
|
(– ∞; – 3) |
(– 3; – 1) |
(– 1; 1) |
(1; 3) |
(3; +∞) |
Обчисліть значення виразу log3 45 + log3 900 − log3 500 № 16, 2018
|
А |
Б |
В |
Г |
Д |
|
|
4 |
3 |
27 |
log3 445 |
Укажіть проміжок, якому належить число log2 9 № 14, 2017
|
А |
Б |
В |
Г |
Д |
|
(0; 1) |
(1; 2) |
(2; 3) |
(3; 4) |
(4; 5) |
|
А |
Б |
В |
Г |
Д |
log3 54 − log3 2 = № 6, 2016д
|
А |
Б |
В |
Г |
Д |
|
log3 52 |
3 |
9 |
24 |
27 |
log2 5 + log2 1,6 = № 14, 2016
|
А |
Б |
В |
Г |
Д |
|
3 |
3,3 |
0,25 |
4 |
log2 6,6 |
![]() № 16, 2015_ІІ
№ 16, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
0,25 |
–1 |
0,5 |
–2 |
–0,25 |
Укажіть проміжок, якому належить число log5 4 № 18, 2015_І
|
А |
Б |
В |
Г |
Д |
|
(0; 1) |
(1; 2) |
(2; 3) |
(3; 4) |
(4; 5) |
lg 25
![]() = № 11, 2013_ІІ
= № 11, 2013_ІІ
lg 5
|
А |
Б |
В |
Г |
Д |
|
lg 5 |
5 |
lg 20 |
2 |
0,5 |
5
log5 49 + 2 log5 7 № 18, 2013_І
|
25 |
log5 70 |
|
log5 35 |
2 |
1
Обчисліть log2 8![]() + log5 25 № 6, 2011
+ log5 25 № 6, 2011
|
А |
Б |
В |
Г |
Д |
|
2 |
–1 |
5 |
|
|
Обчисліть log3 18 − log3 2 № 9, 2010_І
|
А |
Б |
В |
Г |
Д |
|
2 |
3 |
log3 16 |
6 |
9 |
![]()
Обчисліть log𝑎 √𝑎𝑏, якщо log𝑎 𝑏 = 7 № 12, 2008
|
А |
Б |
В |
Г |
Д |
|
|
2 |
3 |
|
4 |
|
А |
|
|
|
|
|
Б |
В |
Г |
Д |
|
|
|
|
–2 |
|
|
Обчисліть № 11, 2007
5
Обчисліть значення виразу log5 49 + 2 log5 7 № 7, 2006
|
А |
Б |
В |
Г |
Д |
|
0 |
1 |
2 |
4 |
25 |
|
Завдання відкритої форми з короткою відповіддю |
|
|
Обчисліть 4001−log20 4 |
№ 27, 2021д |
Обчисліть значення виразу ![]() № 33, 2015_І
№ 33, 2015_І
𝑥 1
Якщо додатні числа х і у задовольняють умову ![]() , то: № 27, 28, 2014д,
, то: № 27, 28, 2014д,
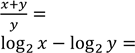 1.
1.
2.
|
Відповідь надайте у вигляді двох чисел, розділених крапкою з комою. |
|
|
Обчисліть (√20) 20 16
|
№ 29, 2012_ІІ |
Обчисліть значення виразу ![]() . № 28, 2012_І
. № 28, 2012_І
|
|
|
|
Знайдіть значення виразу 62 log6 9−log6 4 |
№ 29, 2010_ІІ |
Обчисліть log3 4 ∙ log4 5 ∙ log5 7 ∙ log7 81 № 29, 2007
Обчисліть ![]() . Відповідь запишіть ДЕСЯТКОВИМ ДРОБОМ № 28, 2006
. Відповідь запишіть ДЕСЯТКОВИМ ДРОБОМ № 28, 2006
Обчисліть log2 3 ∙ log3 4 ∙ log4 5 ∙ log5 6 ∙ log6 7 ∙ log7 8 № 23, 2005
ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ. ТОТОЖНІ ПЕРЕТВОРЕННЯ
ВИРАЗІВ
Завдання з вибором однієї правильної відповіді
Спростіть вираз 2(𝑥 + 5𝑦) − (4𝑦 − 7𝑥) № 7, 2021д
|
А |
Б |
В |
Г |
Д |
|
9𝑥 + 𝑦 |
9𝑥 + 14𝑦 |
−5𝑥 + 6𝑦 |
9𝑥 + 6𝑦 |
16𝑥 + 2𝑦 |
3𝑚−2𝑛 3𝑚
![]() Спростіть вираз − . № 6, 2021
Спростіть вираз − . № 6, 2021
8 8
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
3𝑚 − 𝑛
4 |
𝑥 + 2(𝑥 − 2) = № 1, 2020д
|
А |
Б |
В |
Г |
Д |
|
3𝑥 − 4 |
3𝑥 + 4 |
3𝑥 |
3𝑥 − 2 |
2𝑥 − 2 |
Укажіть вираз, тотожно рівний виразу (2𝑥 − 3)2 + 12𝑥. № 9, 2020д
|
А |
Б |
В |
Г |
Д |
|
4𝑥2 + 12𝑥 − 9 |
4𝑥2 + 9 |
4𝑥2 − 9 |
4𝑥2 + 12𝑥 + 9 |
4𝑥2 + 6𝑥 + 9 |
Розкладіть на множники (𝑥 + 𝑦)2 − 9𝑥2 № 12, 2020
|
А |
(−8𝑥 + 𝑦)(10𝑥 + 𝑦) |
|
Б |
(−2𝑥 − 𝑦)(4𝑥 − 𝑦) |
|
В |
(−2𝑥 + 𝑦)(4𝑥 + 𝑦) |
|
Г |
(4𝑥 + 𝑦)2 |
|
Д
|
(−2𝑥 + 𝑦)2 |
Спростіть вираз 2𝑎 − (3𝑏 − 2𝑎) № 1, 2019д
|
А |
Б |
В |
Г |
Д |
|
−3𝑏 |
4𝑎 − 3𝑏 |
−6𝑎𝑏 − 4𝑎 |
−6𝑎𝑏 + 4𝑎 |
−6𝑎𝑏 − 4𝑎2 |
Спростіть вираз ![]() № 11, 2019д
№ 11, 2019д
|
А |
Б |
В |
Г |
Д |
|
3 − 𝑥
𝑥 + 3 |
𝑥 − 3
𝑥 + 3 |
3 − 𝑥 |
1
𝑥 + 3 |
|
Спростіть вираз 0,8𝑏9: (8𝑏3), де 𝑏 ≠ 0 № 1, 2019
𝑎2−𝑏
|
А |
Б |
В |
Г |
Д |
|
0,1𝑏6 |
10𝑏6 |
6,4𝑏12 |
0,1𝑏3 |
10𝑏3 |
|
2
|
|
|
|
|
|
А |
Б |
В |
Г |
Д |
|
𝑎 + 𝑏
𝑎 |
𝑎 − 𝑏
𝑎 |
|
𝑏 |
𝑎 + 𝑏
𝑏 |
|
3𝑥 + 3𝑦 = |
63, то 𝑥 − |
𝑦 = |
|
|
|
А |
Б |
В |
Г |
Д |
|
14 |
147 |
|
−3 |
|
Скоротіть дріб 𝑎2−𝑎𝑏 № 12, 2019 Якщо 𝑥2 − 𝑦2 = 7 і № 12, 2018д
![]() 2
2
Укажіть проміжок, якому належить значення виразу (1 − √2) . № 17, 2018д
|
А |
Б |
В |
Г |
Д |
|
(−3; 0) |
[0; 0,5) |
[0,5; 1) |
[1; 2) |
[2; 5) |
![]() № 1, 2018
№ 1, 2018
|
А |
Б |
В |
Г |
Д |
|
𝑎 + 2 |
2𝑎 + 1 |
𝑎 + 1 |
2𝑎 |
𝑎 |
Спростіть вираз 𝑎(𝑎 + 2𝑏) − (𝑎 + 𝑏)2 № 10, 2018
|
А |
Б |
В |
Г |
Д |
|
4𝑎𝑏 + 𝑏2 |
4𝑎𝑏 − 𝑏2 |
−𝑏2 |
2𝑎𝑏 − 𝑏2 |
𝑏2 |
Укажіть вираз, тотожно рівний виразу 𝑥2 + 4. № 10, 2017д
|
А |
Б |
В |
Г |
Д |
|
(𝑥 + 2)(𝑥 − 2) |
𝑥(𝑥 − 2) |
(𝑥 + 2)2 + 4𝑥 |
(𝑥 + 2)2 |
(𝑥 − 2)2 + 4𝑥 |
Якщо числа х і у задовольняють співвідношення 2𝑦 + 4 = 𝑥, то 𝑦 = № 1, 2017
|
А |
Б |
В |
Г |
Д |
|
2𝑥 − 8 |
8 − 2𝑥 |
𝑥 − 4
2 |
𝑥 + 4
2 |
4 − 𝑥
2 |
𝑎2+16 8𝑎
![]() Спростіть вираз: − № 7, 2017
Спростіть вираз: − № 7, 2017
𝑎−4 𝑎−4
|
А |
Б |
В |
Г |
Д |
|
–1 |
а – 4 |
а + 4 |
1 |
(а – 4)2 |
Розкладіть на множники вираз (𝑎 − 1)2 − (𝑏 − 1)2 № 8, 2016д
|
А |
(𝑎 − 𝑏)(𝑎 + 𝑏) |
|
Б |
(𝑎 − 𝑏)(𝑎 + 𝑏 + 2) |
|
В |
(𝑎 − 𝑏)2 |
|
Г |
(𝑎 − 𝑏)(𝑎 + 𝑏 − 2) |
|
Д |
(𝑎 + 𝑏)(𝑎 − 𝑏 − 2) |
1 2𝑥−5
![]() Спростіть вираз − № 12, 2016д
Спростіть вираз − № 12, 2016д
𝑥−5 𝑥(𝑥−5)
|
А |
Б |
В |
Г |
Д |
|
|
𝑥 − 5 − 𝑥(𝑥 − 5) |
4
𝑥 − 5 |
10 − 𝑥
𝑥(𝑥 − 5) |
|
Спростіть вираз: ![]() № 11, 2016
№ 11, 2016
|
А |
Б |
В |
Г |
Д |
|
𝑎 + 𝑏
𝑎𝑏 |
|
1
𝑏 − 𝑎 |
𝑎 − 𝑏
𝑎𝑏 |
0 |
Розкладіть на множники вираз 25𝑥2 − 1 № 6, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
(25𝑥−1)(𝑥+1) |
(5𝑥−1)2 |
(5𝑥−1)(5𝑥+1) |
5(𝑥−1)(𝑥+1) |
25(𝑥−1)(𝑥+1) |
2(5𝑥 + 6) = № 1, 2015_І
|
А |
Б |
В |
Г |
Д |
|
10х +12 |
10х + 6 |
7х + 8 |
7х + 12 |
5х + 8 |
−2𝑥𝑦2 − (3𝑥𝑦2 − 2𝑥2𝑦) = № 2, 2014д
|
А |
Б |
В |
Г |
Д |
|
−5𝑥𝑦2 + 2𝑥2𝑦 |
−5𝑥𝑦2 − 2𝑥2𝑦 |
𝑥𝑦2 − 2𝑥2𝑦 |
−6𝑥𝑦2 + 2𝑥2𝑦 |
−3𝑥𝑦2 |
Спростіть вираз ![]() № 10, 2014_д
№ 10, 2014_д
𝑎
|
А |
Б |
В |
Г |
Д |
|
𝑎(𝑎 − 1) |
−𝑎3 |
−𝑎(𝑎 + 1) |
𝑎 + 1
𝑎 |
𝑎(𝑎 + 1) |
Якщо 𝑥 + 2𝑦 − 6𝑧 =– 1 і − 𝑦 + 3𝑧 = 5, то 𝑥 = № 9, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
9 |
11 |
4 |
–9 |
–11 |
![]()
![]()
![]() Знайдіть значення виразу 1 − 1 , якщо √3𝑎−√3𝑏 = √12 № 13, 2013_ІІ
Знайдіть значення виразу 1 − 1 , якщо √3𝑎−√3𝑏 = √12 № 13, 2013_ІІ
𝑏 𝑎 𝑎𝑏
|
А |
Б |
В |
Г |
Д |
|
–2 |
0,5 |
2 |
3 |
6 |
Укажіть вираз, тотожно рівний виразу (2𝑥 + 5) ∙ (3 − 𝑥) № 2, 2013_І
|
А |
Б |
В |
Г |
Д |
|
15 + 𝑥 − 2𝑥2 |
15 + 𝑥 + 2𝑥2 |
15 + 6𝑥 − 2𝑥2 |
15 + 11𝑥 − 2𝑥2 |
15 + 11𝑥 + 2𝑥2 |
Обчисліть 10012 − 9992 № 1, 2010_ІІ
|
А |
Б |
В |
Г |
Д |
|
2 |
4 |
2000 |
3980 |
4000 |
|
3𝑥+12
|
|
|
|
|
|
А |
Б |
В |
Г |
Д |
Спростіть вираз № 1, 2009
|
3
4 − 𝑥 |
3
𝑥 + 4 |
3
𝑥 − 4 |
3 − 𝑥 + 4 |
1
𝑥 − 4 |
![]() √9+𝑎2−6𝑎
√9+𝑎2−6𝑎
Знайдіть значення виразу , якщо 𝑎 = 2,5 № 20, 2008
𝑎−3
|
А |
Б |
В |
Г |
Д |
|
–1 |
–0,5 |
0 |
0,5 |
1 |
Якщо ![]() , то с = № 2, 2006
, то с = № 2, 2006
|
А |
Б |
В |
Г |
Д |
|
𝑎𝑏
𝑎 − 𝑏 |
𝑎𝑏
𝑏 − 𝑎 |
𝑎 − 𝑏 |
|
𝑎 − 𝑏
𝑎𝑏 |
Знайдіть вираз, тотожно рівний виразу 𝑥4 + 𝑥3 − 𝑥 − 1 № 3, 2006
|
А |
(𝑥 + 1)2(𝑥2 + 𝑥 + 1) |
|
Б |
(𝑥2 − 𝑥 + 1)(𝑥 − 1)2 |
|
В |
(𝑥 − 1)3(𝑥 + 1) |
|
Г |
(𝑥 − 1)(𝑥 + 1)3 |
|
Д
|
(𝑥2 − 1)(𝑥2 + 𝑥 + 1) |
Завдання на встановлення відповідності
![]()
Увідповідніть вираз (1–3) із його значенням (А–Д), якщо 𝑥 = √5 − 1. № 18, 2021д
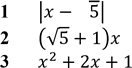 √ А –1
√ А –1
Б 1
В 4 Г 5
Д 6
До кожного виразу (1–4) доберіть тотожно йому рівний (А–Д), якщо 𝑚 > 2, 𝑚 –
|
натуральне число.
|
№ 21, 2014 |
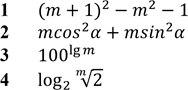 А 0
А 0
Б m
В 2m
Г ![]()
Д ![]()
𝑚
До кожного виразу (1–4) доберіть тотожно рівний йому вираз (А–Д). № 21, 2012_ІІ
1 (𝑎 − 8)(𝑎 + 8) А 𝑎2 − 16𝑎 + 64
2 (𝑎 − 8)2 Б 𝑎2 − 64
3 (𝑎 − 4)(𝑎2 + 4𝑎 + 16) В 𝑎2 − 20𝑎 + 64
4 (𝑎 − 4)(𝑎 − 16) Г 𝑎3 + 64
Д 𝑎3 − 64
Установіть відповідність між виразами (1–4) та їхніми значеннями, якщо х = 0,5 (А–Д).
№ 28, 2011
Вираз Значення виразу
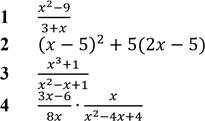 А –2,5
А –2,5
Б –0,25
В 0,25
Г 1,5
Д 2,5
Завдання відкритої форми з короткою відповіддю
Обчисліть значення виразу ![]() при 𝑎 = 0,1,𝑏 = 3,7 № 31, 2015_ІІ
при 𝑎 = 0,1,𝑏 = 3,7 № 31, 2015_ІІ
Обчисліть значення виразу ![]() при 𝑎 = 0,25,𝑏 = 4,5. № 31, 2015_І
при 𝑎 = 0,25,𝑏 = 4,5. № 31, 2015_І
Знайдіть значення виразу ![]() № 27, 2013_ІІ
№ 27, 2013_ІІ
Обчисліть значення виразу ![]() , якщо 𝑎 = 10,2,𝑏 = −0,2. № 26, 2013_І
, якщо 𝑎 = 10,2,𝑏 = −0,2. № 26, 2013_І
Знайдіть значення виразу ![]() , якщо 𝑚 = 4,25. № 29, 2010_І
, якщо 𝑚 = 4,25. № 29, 2010_І
![]() 4
4
Спростіть вираз № 15, 2005
Завдання відкритої форми з розгорнутою відповіддю
Доведіть тотожність ![]() № 33, 2021д
№ 33, 2021д
Доведіть тотожність ![]() № 33, 2021
№ 33, 2021
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ. ОСНОВНІ ТРИГОНОМЕТРИЧНІ
ТОТОЖНОСТІ
Завдання з вибором однієї правильної відповіді
7−(sin2𝛽+cos2𝛽)
![]() 2𝛽+3cos2𝛽 = № 10, 2021д 3sin
2𝛽+3cos2𝛽 = № 10, 2021д 3sin
|
А |
Б |
В |
Г |
Д |
|
|
|
|
12 |
2 |
sin2 2𝑥 = № 14, 2021
|
А |
Б |
В |
Г |
Д |
|
2 sin2 𝑥 |
4 sin2 𝑥 |
4 sin2 𝑥 cos2 𝑥 |
2 sin2 𝑥 cos2 𝑥 |
sin 4𝑥2 |
cos𝛼tg𝛼
![]() 2𝛼 = № 13, 2020д
2𝛼 = № 13, 2020д
sin
|
А |
Б |
|
Г |
Д |
|
sin 𝛼 |
1
sin2 𝛼 |
|
cos 𝛼 |
1 |
Спростіть вираз (1 + tg2𝛼)sin2𝛼 № 14, 2020
|
А |
Б |
В |
Г |
Д |
|
|
1 |
cos2𝛼sin2𝛼 |
cos2𝛼 |
tg2𝛼 |
Спростіть вираз 2 sin2 𝛼 ∙ ctg 𝛼 № 13, 2019д
|
А |
Б |
В |
Г |
Д |
|
cos 2𝛼 |
2cos 2𝛼 |
|
2 sin 2𝛼 |
sin 2𝛼 |
Спростіть вираз (1 − sin2 𝛼) ∙ tg2 𝛼 № 10, 2019
|
А |
Б |
|
Г |
Д |
|
sin 2𝛼 |
cos 2𝛼 |
|
sin2 𝛼 |
ctg2 𝛼 |
cos(900+𝛼)
![]() = № 10, 2018д
= № 10, 2018д
sin𝛼
|
А |
Б |
В |
Г |
Д |
|
−1 |
ctg𝛼 |
tg𝛼 |
−ctg𝛼 |
1 |
1 − sin 𝛼 ctg 𝛼 cos 𝛼 = № 13, 2018
|
А |
Б |
|
Г |
Д |
|
cos 2𝛼 |
1 − sin 2𝛼 |
cos2𝛼 |
sin2𝛼 |
Якщо 2sin𝛼 = cos𝛼, то tg𝛼 = № 15, 2017д
|
А |
Б |
В |
Г |
Д |
|
–2 |
–0,5 |
0,2 |
0,5 |
2 |
1 − sin2𝛼 − cos2𝛼 = № 12, 2017
|
А |
Б |
В |
Г |
Д |
|
–2 |
0 |
1 |
2cos2α |
1 + cos2α |
Обчисліть значення виразу ![]() , якщо
, якщо ![]() № 16, 2016д
№ 16, 2016д
|
А |
Б |
В |
Г |
Д |
|
50 |
5 |
2 |
1 |
|
Обчисліть значення виразу 4sin2𝛼, якщо 4cos2𝛼 = 1. № 17, 2016
|
А |
Б |
В |
Г |
Д |
|
0 |
|
|
3 |
4 |
Якому проміжку належить значення виразу sin 4150? № 7, 2015_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Спростіть вираз 1![]() +tg1 2α № 10, 2015_І
+tg1 2α № 10, 2015_І
|
А |
Б |
В |
Г |
Д |
|
cos2α |
sin2α |
tg2α |
ctg2α |
1 |
Спростіть вираз (1 − cos2α)ctg2α № 16, 2014д
|
А |
Б |
В |
Г |
Д |
|
cos2α |
sin2α |
sin4α
cos2α |
sin2α |
tg2α |
Відомо, що ctg𝛼 < 0, cos𝛼 > 0. Якого значення може набувати sin𝛼? № 14, 2014
|
А |
Б |
В |
Г |
Д |
|
–1 |
|
0 |
|
1 |
Спростіть вираз sin2 α(1 − ctg2α) № 17, 2013_ІІ
|
А |
Б |
В |
Г |
Д |
|
cos(2α) |
tg2α |
1 |
ctg2α |
−cos(2α) |
Укажіть нерівність, що виконується для 𝛼 ∈ (𝜋 ; 𝜋) № 19, 2013_І
2
|
А |
Б |
В |
Г |
Д |
|
1 − sin2 𝛼 < 0 |
cos𝛼 ∙ tgα < 0 |
cos2 𝛼 + sin2 𝛼 < 0 |
1 − cos2 𝛼 < 0 |
sinα ∙ ctgα < 0 |
Укажіть проміжок, якому належить значення виразу ctg250 № 15, 2012_ІІ
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Якому проміжку належить значення виразу sin4100? № 13, 2012_І
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
На одиничному колі зображено точку Р(–0,8; 0,6) і кут α (див. рисунок). Визначте cos 𝛼.
№9, 2011
|
А |
Б |
В |
Г |
|
|
–0,8 |
0,6 |
0,8 |
–0,6 |
Обчисліть sin2100 № 7, 2010_ІІ
|
А |
Б |
|
Г |
Д |
|
|
|
|
|
|
Спростіть вираз (1 − cos2 α)ctg2α № 13, 2010_І
|
А |
Б |
|
Г |
Д |
|
cos2 α |
sin2α |
|
sin2 α |
tg2 α |
Обчисліть ![]() № 8, 2008
№ 8, 2008
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
Інша відповідь |
Укажіть найменший додатний період функції 𝑦 = 2ctg(3𝑥) № 9, 2008
|
А |
Б |
В |
Г |
Д |
|
2𝜋 |
𝜋 |
|
|
|
![]()
Обчисліть √(2 sin 450 + 1)2 − √(1 − 2cos450)2 № 7, 2007
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
√2 |
2 |
Знайдіть множину значень функції 𝑓(𝑥) = (sin𝑥 + cos 𝑥)2. № 9, 2006
|
А |
Б |
В |
Г |
Д |
|
[1; 2] |
[0; 2] |
[−√2; √2] |
[0; 1] |
Інша відповідь |
Обчисліть значення виразу sin α + sin β, якщо α − β = 1800. № 12, 2006
|
А |
Б |
В |
Г |
Д |
|
1 |
|
0 |
|
Інша відповідь |
Завдання відкритої форми з короткою відповіддю
Обчисліть значення виразу 2sinαcosα, якщо sinα + cosα = 1,2. № 31, 2014д
Знайдіть найбільше значення функції![]() № 28, 2013_ІІ
№ 28, 2013_ІІ
Знайдіть найменший додатний період функції 𝑓(𝑥) = 9 − 6cos (20𝜋𝑥 + 7). № 28, 2013_І
Обчисліть cos 𝛼, якщо ![]() № 23, 2009
№ 23, 2009
Знайдіть найбільше значення функції ![]() . Якщо функція не має найбільшого значення, то у відповідь запишіть число 100. № 30, 2009
. Якщо функція не має найбільшого значення, то у відповідь запишіть число 100. № 30, 2009
Обчисліть ![]() № 26, 2008
№ 26, 2008
Обчисліть 2 sin 150 cos 150 tg300ctg300 № 25, 2007
Обчисліть значення виразу sin2𝛼, якщо ![]() . Відповідь запишіть десятковим дробом № 25, 2006
. Відповідь запишіть десятковим дробом № 25, 2006
Спростіть вираз (tg 𝛼 + ctg 𝛼) sin 2𝛼 № 14, 2005
Обчисліть значення виразу 20 (sin 𝛼 − cos 𝛼), якщо ![]()
№ 21, 2005


про публікацію авторської розробки
Додати розробку