Методи розв'язування показникових нерівностей

Простейшие показательные неравенства, вида:

.

Метод решения: применение  свойств убывания или возрастания показательной  функции

Пример 1. Решите неравенство .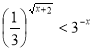

Решение

1-й способ

Преобразуем неравенство: . Показательная функция с основанием 3 является возрастающей, значит .

Правая часть неравенство может быть как отрицательной, так и неотрицательной.

Если правая часть отрицательна, тогда получим систему неравенств:

.

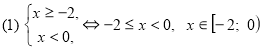Если правая часть неотрицательна, то получим систему неравенств:

 (2) .

.

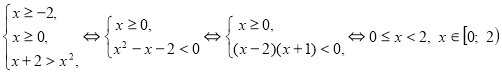Ответ: .

 

2-й способ (метод интервалов)

 

Преобразуем неравенство: .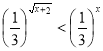

Показательная функция с основанием является убывающей, значит .

Преобразуем полученное иррациональное неравенство: .

Рассмотрим функцию и найдем значения x, при которых функция принимает положительные значения.

Область определения функции: .

Функция непрерывна на промежутке .

Найдем нули функции: f(x) = 0,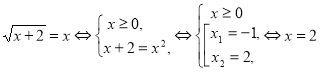

Определим знак функции на каждом из промежутков:

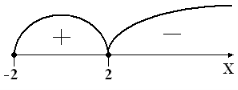
Рис. 1

 

f(-2) = 2 > 0, , f(2) = 0, а(7) = -4 < 0.

 

Ответ: .

 

Пример 2. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 0,5 является убывающей, значит .

Ответ: .

 

Пример 3. Решите неравенство .

Решение

Преобразуем неравенство: .

Решая это неравенство методом промежутков, получим .

Ответ: .

 

Пример 4. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 2 является возрастающей, значит .

Ответ: .

 

Пример 5. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 3 является возрастающей, значит .

Ответ: .

 

Пример 6. Решите неравенство .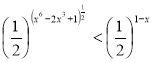

Решение

Показательная функция с основанием является убывающей, значит:

.

Преобразуем неравенство: .

Трехчлен при всех , так как его дискриминант отрицателен, а первый коэффициент положителен. Получим:

Правая часть неравенства может быть отрицательной, так и неотрицательной.

1. Если x - 1 > 0, тогда получим систему неравенств:

 

,

 

.

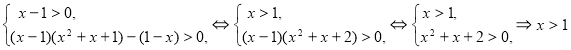2. Если , то получим систему неравенств:

 

 

 

 

 

 

 

 

 

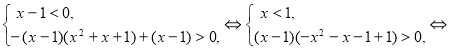
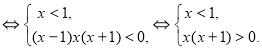
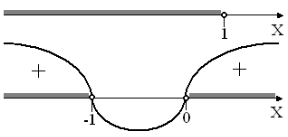
Рис. 2

 

.

3. Если 1 - x = 0, то x = 1, а неравенство примет вид 1 < 1, которое не выполняется.

 

Ответ: .

 

Пример 7. Решите неравенство .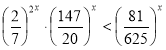

Решение

Преобразуем неравенство: ,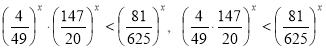

.

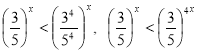Показательная функция с основанием является убывающей, значит,  x > 4x или x<0.

Ответ: .

 

 

Пример 8. Решите неравенство .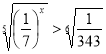

Решение

Преобразуем неравенство: 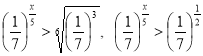. Показательная функция с основанием является убывающей, значит, .

 

Ответ: .

 

Пример 9. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 2 является возрастающей, получим - это иррациональное неравенство со знаком ">", которое равносильно системе неравенств:

.

Ответ: .

 

Пример 10. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 2 является возрастающей, получим иррациональное неравенство.

, которое равносильно системе неравенств:

.

Ответ: .

 

Пример 11. Решите неравенство .

Решение

1-й способ

Преобразуем неравенство . Показательная функция с основанием 5 является возрастающей, получим иррациональное неравенство со знаком ">",

,

правая часть, которого может быть как отрицательной, так и неотрицательной.

1. Если правая часть отрицательна, тогда неравенство равносильно системе:

  - система не имеет решений.

2. Если правая часть положительна, тогда неравенство равносильно системе:

 

 

 

 

 

 

 

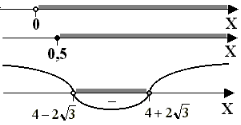
Рис. 3

 

3. Если правая часть равна нулю, т. е. x = 0, тогда -  не существует и неравенство  не имеет решений.

Ответ: .

 

2-й способ (метод интервалов)

Преобразуем неравенство . Показательная функция с основанием 5 является возрастающей, получим иррациональное неравенство

.

Полученное неравенство преобразуем к виду: .

Рассмотрим функцию и найдем значения x, при которых функция положительна.

Область определения этой функции: .

Эта функция непрерывна на промежутке .

Определим нули функции:

f(x) = 0,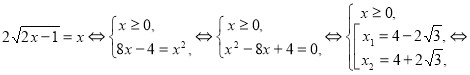

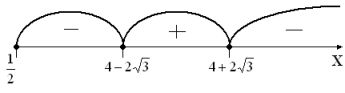
Рис. 4

 

 

, , .

 

Ответ: .

 

Пример 12. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 2 является возрастающей, значит, |x| < 10 или  -10 < x < 10.

Ответ: (-10; 10).

 

Пример 13. Решите неравенство .

Решение

Преобразуем неравенство: . Показательная функция с основанием 0,3 является убывающей, значит: .

Замечаем, что - бесконечная убывающая геометрическая прогрессия с первым членом и знаменателем, равным .

Сумма ее членов равна: , , 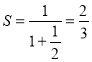получим неравенство:

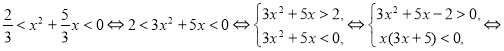
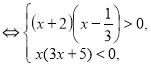
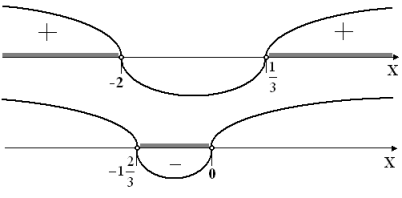
Рис. 5

Ответ: решений нет.

 

 

 

Пример 14. Решите неравенство .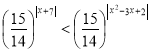

Решение

Показательная функция с основанием является возрастающей, значит:

. Преобразуем неравенство: .

Рассмотрим функцию f(x) = |x + 7| - |(x - 1)(x - 2)| и найдем значения x, при которых функция принимает отрицательные значения.

Область определения этой функции - множество всех действительных чисел:

.

Функция непрерывна на множестве всех действительных чисел.

Значения x, при которых модули обращаются в нуль: -7, 1 и 2.

Определим знак функции на каждом из этих промежутков.

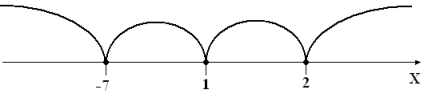
Рис. 6

При , получим ,

.

Найдем нули функции на этом промежутке:

f(x) = 0, , квадратный трехчлен корней не имеет, значит функция на этом промежутке не имеет нуле и имеет постоянный знак: f(-8)=-89<0.

При x = -7, f(-7) = -72 < 0.

При , получим ,

.

Найдем нули функции на этом промежутке:

.

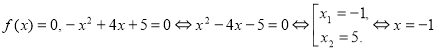Найдем знаки функции на следующих промежутках:

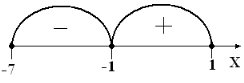
Рис. 7

f(-5) = -40 < 0, f(-1) = 0, f(0) = 5 > 0, f(1) = 8 > 0.

При , получим ,

- функция нулей не имеет на этом промежутке, а значит, будет иметь постоянный знак: f(1,5) = 8,25 > 0, f(2) = 9 > 0.

При , получим .

Найдем нули функции на этом промежутке:

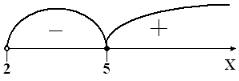
Рис. 8

f(3) = -8 < 0, f(5) = 0, f(7) = 16 > 0.

.

Ответ: .

II вид. Неравенства, содержащие одинаковые степени. Метод решения: вынесения общего множителя за скобки применение свойств показательной функции.

 

Пример 26. Решите неравенство .

Решение

Преобразуем неравенство: .

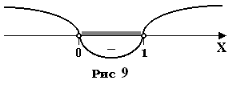Показательная функция с основанием 3 является возрастающей, значит, ,

 

 

 

Ответ: .

 

Пример 27. Решите неравенство .

Решение

Преобразуем неравенство:

. Показательная функция с основанием 3 является возрастающей, значит, .

 

Ответ: .

 

Пример 28. Решите неравенство .

Решение

Преобразуем неравенство:

.

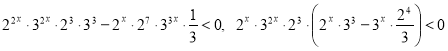Поскольку , тогда полученное неравенство равносильно неравенству:

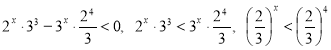. Показательная функция с основанием является убывающей, тогда x > 4.

Ответ: .

III. Неравенства, содержащие степени с одинаковыми и разными основаниями и разными показателями. Метод решения: приведение к алгебраическим заменой переменных

 

Пример 31. Решите неравенство .

Решение

Преобразуем неравенство, зная, что :

. Пусть , получим систему неравенств:

 

 

 

 

 

 

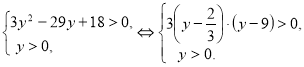
Рис. 10

. Получим совокупность неравенств:

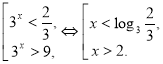
При решении совокупности были использованы свойства показательной функции с основанием 3 (она возрастает) и логарифмической функции с основанием 3 (она также является возрастающей).

Ответ: .

 

 

 

Пример 32. Решите неравенство .

Решение

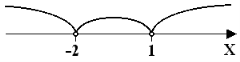Отложим на числовой прямой точки, в которых каждый из модулей, находящихся в показателе равны нулю:

 

 

Рис. 11

Рассмотрим неравенство на каждом из этих промежутков.

1. Если x < -2, тогда получим неравенство: ,

.

Приходим к системе неравенств:  или .

2. Если , тогда получим неравенство: ,

. Пусть , тогда получим систему неравенств: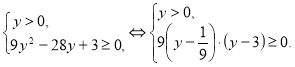

 

 

 

 

 

 

Рис. 12

Решением системы является совокупность неравенств и , которая равносильна:   .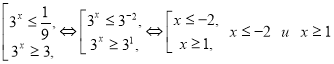

Получим систему неравенств: .

3. Если , тогда получим неравенство: ,

или .

Решением неравенства является объединение промежутков:

 

.

 

Ответ: .

 

Пример 33. Решите неравенство .

Решение

Преобразуем неравенство: . Положим , получим систему неравенств:

 

 

 

 

 

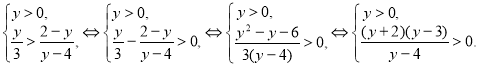
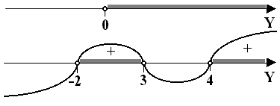
Рис. 13

Решением системы является объединение промежутков: и .

Получим совокупность неравенств: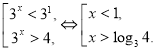

При решении неравенств использовались свойство показательной функции с основанием 3 возрастать и логарифмической функции с тем же основанием также возрастать.

Ответ: .

Пример 34. Решите неравенство .

Решение

Преобразуем неравенство: .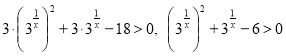

Пусть , получим систему неравенств:

 

 

 

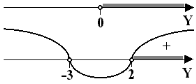
        Рис. 14

Решением системы является неравенство . Выполняя обратную подстановку, получим неравенство:

.

 

 

 

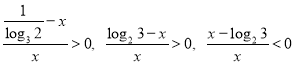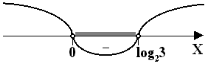
Рис. 15  Ответ: .

Пример 35. Решите неравенство .

Решение

Преобразуем неравенство: . Пусть , тогда получим систему неравенств:

 

 

 

 

 

 

 

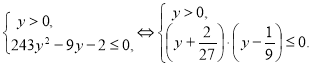
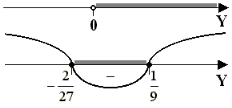
Рис. 16

Решением системы является неравенство .

Отсюда получим: .

 

Ответ: .

 

Пример 36. Решите неравенство .

Решение

Преобразуем неравенство . Пусть , тогда получим систему уравнений:

 

 

 

 

 

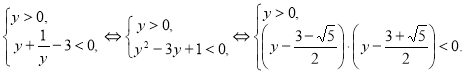
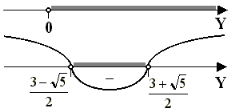
Рис. 17

Решением системы является промежуток .

Отсюда находим: . Логарифмическая функция с основанием 2 является возрастающей, поэтому .

 

Ответ: .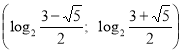

 

Пример 37. Решите неравенство .

Решение

Преобразуем неравенство . Положим получим систему неравенств:

 

 

 

 

 

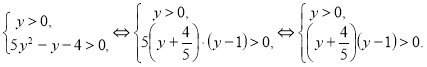
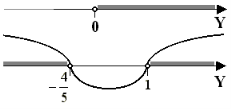
Рис. 18

Получим неравенство , поскольку показательная функция с основанием 5 является возрастающей.

Ответ: .

 

Пример 38. Решите неравенство .

Решение

Положим , получим систему неравенств:

 

 

 

 

 

 

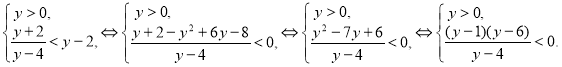
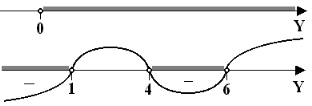
Рис. 19

Решением системы является совокупность неравенств:

 

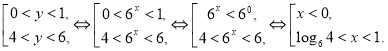
Ответ: .

 

Пример 39. Решите неравенство .

Решение

Преобразуем неравенство: . Пусть , получим систему неравенств:

 

 

 

 

 

 

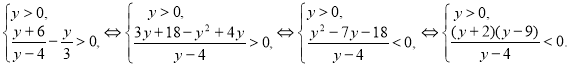
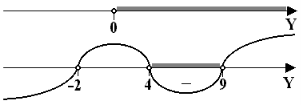
Рис. 20

Получим двойное неравенство 4 < y < 9 или .

Показательная и логарифмическая функции с основанием 3 являются возрастающими.

 

Ответ: .

 

Пример 40. Решите неравенство .

Решение

Пусть , t > 0, тогда получим , получим:

Вернемся к переменной x:

.

Поскольку - функция возрастающая, то

откуда .

Ответ: .

Замечание. Можно не делать замену переменной, а вынести за скобки общий множитель

 

Пример 41. Решите неравенство .

Решение

Сделав замену , t > 0, получим неравенство второй степени относительно t:

.

Вернемся к переменной x: . Так как основание степени больше единицы, то и  .

 

Ответ: .

 

IV вид. Неравенства, содержащие переменную в основании степени. Метод решения: исследование возможных трех случаев значений основания степени

 

Пример 47. Решите неравенство .

Решение

Рассмотрим три случая.

I-й случай, когда основание степени больше нуля, но меньше 1, т. е. 0 < x - 4 < 1.

Неравенство примет вид: . Показательная функция с таким основанием убывает, получим систему неравенств:

решений нет.

II-й случай, когда основание степени равно единице x - 4 = 1, x = 5, получим:

- неравенство не выполняется.

 

III-й случай, когда основание степени больше единице, тогда неравенство равносильно системе неравенств:

 

.

 

Ответ: .

 

Пример 48. Решите неравенство .

Решение

Рассмотрим три случая.

I-й случай, когда основание степени больше нуля, но меньше 1, т. е. 0 < x + 5 <1.

Неравенство примет вид: . Показательная функция с таким основанием убывает, получим систему неравенств:

решений нет.

II-й случай, когда основание степени равно единице x + 5 = 1, x = -4, получим:

- неравенство не выполняется.

III-й случай, когда основание степени больше единице, тогда неравенство равносильно системе неравенств:

 

Ответ: .

 

 

 

Пример 49. Решите неравенство .

Решение

Рассмотрим три случая.

I-й случай, когда основание степени больше нуля, но меньше 1, т. е. 0 < x + 3 < 1.

Неравенство примет вид: . Показательная функция с таким основанием убывает, получим систему неравенств:

решений нет.

II-й случай, когда основание степени равно единице x + 3 = 1, x = -2, получим:

- неравенство не выполняется.

III-й случай, когда основание степени больше единице, тогда неравенство равносильно системе неравенств:

.

Ответ: .