Методична розробка бінарного уроку з математики та історії. Тема: «Тригонометричні функції. Повторення. Сім чудес античного світу.»

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

БЕРДЯНСЬКИЙ ЕКОНОМІКО-ГУМАНІТАРНИЙ КОЛЕДЖ

БЕРДЯНСЬКОГО ДЕРЖАВНОГО ПЕДАГОГІЧНОГО УНІВЕРСИТЕТУ

 

 

 

 

 

 

 

МЕТОДИЧНА РОЗРОБКА БІНАРНОГО УРОКУ З МАТЕМАТИКИ ТА ІСТОРІЇ

Тема:

«Тригонометричні функції. Повторення. Сім чудес античного світу.»

 

 

Виконав викладач математики

Костюкович Вікторія Володимирівна

 

 

 

Тема уроку: Тригонометричні функції. Повторення. Сім чудес античного світу.

Тип уроку: Повторення, узагальнення, систематизація матеріалу.

Форма уроку: інтегрований.

Мета уроку: Повторити матеріал з розділу «Тригонометричні функції», а саме: значення тригонометричних функцій кутів 0⁰,30⁰,45⁰,60⁰,90⁰, формули перетворення градусів у радіани і навпаки, побудову кутів (додатних, від’ємних, більших за 360⁰) та знаходження значень тригонометричних функцій на одиничному колі, графіки тригонометричних функцій та правила їх перетворень, основні тригонометричні тотожності, формули зведення, формули додавання, значення обернених тригонометричних функцій додатних та від’ємних чисел; надання цікавої інформації про сім чудес античного світу.

Сприяти розвитку уваги, пам’яті, логічного мислення, уяви учнів, пізнавальної діяльності.

Виховувати математичну культуру запису та мови, культуру поведінки учнів під час уроку.

Обладнання: Ноутбук, проектор, екран, модель правильної чотирикутної піраміди, презентація «Сім чудес світу», таблиця-стенд «Значення тригонометричних функцій деяких кутів», друковані матеріали – картки із завданнями для учнів, формули перетворення радіан в градуси та навпаки на А2.

 

Хід уроку.

І.  Організація класу (2 хв.).

Перевірка готовності учнів до уроку, відмітка присутніх.

ІІ. Повідомлення теми, мети уроку (1 хв.).

Тема (учні записують у зошит), мета уроку.

ІІІ. Вступна бесіда (1 хв.).

Епіграф до уроку: «Предмет математики настільки серйозний, що не варто втрачати нагоди зробити його трохи цікавішим. (Блез Паскаль)»

Сьогодні  ми не тільки пригадаємо тригонометрію, а й помандруємо у давні часи, ще до н.е., у епоху античності – давній Вавілон, Грецію, Єгипет, та дізнаємось про найвидатніші пам’ятки культури стародавнього світу – які називаються «Сім чудес античного світу».

ІV. Актуалізація знань та вмінь (3хв.).

Але спочатку активізуємо вашу мозкову діяльність - пограємо в «Ланцюжок». (за таблицею «Значення тригонометричних функцій деяких кутів»)

Викладач починає: sin45⁰=, перший учень відповідає і каже новий приклад третьому учню і т.д.

Тепер можна вирушати у подорож.    

V. Подорож. Розв’язування вправ. (35 хв.) 

У багатьох народів стародавнього світу сім вважалося особливим. Наприклад, у єгипетській і вавилонській філософії й астрономії воно розглядалося як сума двох “життєвих чисел”: три й чотири. Пояснювалося це так: троє людей – батько, мати й дитина – становлять основу життя, а чотири – це кількість сторін світу й напрямків вітру, звідки приходить дощ – живильна волога, що робить землю плодоносною.

Отже, число “сім” здавна займало особливе місце в людській уяві, історичній пам'яті та міфології. Мабуть, тому в перших загадках про великі чудеса йшлося саме про сім чудес світу.

I чудо. Перше чудо, з яким ми познайомимось, це Єгипетські піраміди – «загробні будинки» фараонів.(доречі це єдине з семи чудес античного світу, що дійшло до наших днів)

 Серед семи чудес світу єгипетські піраміди найстародавніші. Вони мають правильну форму і тягнуться на десятки кілометрів: від сучасного міста Каїра до Фаюмського оазису.

До наших часів збереглося близько 70 пірамід. Колись їх було ще більше. Найбільша з них - піраміда Хеопса, збудована архітектором Імхотеп у ХХVІІІ ст. до н. е.

 Якщо вірити давньогрецькому історикові Геродоту, 100 тисяч чоловік будували її 20 років. Її складають майже 2,5 млн кам’яних блоків, кожен з яких важить дві з половиною, а то й три тонни. Висота піраміди  – 146.6м, а довжина сторони основи – 233м. У середині знаходилася гробниця фараона. Кажуть, ця піраміда була для нього драбиною, щоб зійти на небо.

Після смерті, фараонів захищали сфінкси – міфічні істоти, у вигляді левів. Їх статуї встановлювалися біля пірамід. За легендами, всім, хто хотів потрапити всередину піраміди, сфінкс загадував загадку. Якщо скарбошукач знаходив відповідь, сфінкс його пропускав, а якщо ні – роздирав. Зараз у Єгипті залишився лише один сфінкс біля піраміди Хеопса.

От і ми будемо уявляти, що перед кожним чудом світу сидить сфінкс і задає нам загадки-завдання. Якщо ми розв’язуємо їх – дізнаємося про нове чудо, якщо ні – задає ще завдання…

I завдання.

Заповнити таблицю:

Градуси		100		270
радіани					2

 

IІ чудо «висячі сади» Семираміди

Далі вирушаємо до Вавилону – найбільшого міста Стародавнього Світу. Там знаходилось ще одне чудо світу «висячі сади» Семираміди.

Легенда, а вслід за нею й описи стародавніх істориків стверджують, що вавилонський цар Навуходоносор ІІ, котрий жив у VІ столітті до нашої ери, влаштував «висячі сади» для своєї коханої дружини – перської царівни, яка надто сумувала у запилюженому й спекотному Вавилоні за зеленими пагорбами своєї батьківщини. Ці сади за своєю красою не мали собі рівних у всьому тодішньому цивілізованому світі. На висоті чотирьохярусної споруди був побудований палац.  На насипних терасах палацу були розбиті "висячі сади". Кожну терасу покривав великий шар чорнозему, в якому могли пускати коріння дерева, кущі, квіти тощо.

 Тут були зібрані рослини з близьких і далеких країн. Ведучи численні завойовницькі походи, Навуходоносор привозив до Вавилону не лише награбовані скарби, а й паростки екзотичних рослин. «Висячі сади» Семираміди становили найбільший і найвидатніший дендрарій (колекція деревних рослин) стародавнього світу…

IІ завдання. На одиничному колі побудувати кути: , , 225⁰, 300⁰, -315⁰, 390⁰. Знайти (за допомогою кола): , .

IІІ чудо. «Храм Артеміди»

Ще одним чудом народи античного світу вважали «Храм Артеміди» у давньогрецькому місті Ефесі. Артеміда – була покровителькою міста Ефеса. Її греки вважали богинею плодоріддя, покровителькою тварин і охоти, богинею Місяця, ціломудрія, охоронителькою породіль. В головному залі храму стояла її статуя висотою понад 2м, вся оздоблена золотом і дорогоцінностями.

Сам же храм являв собою прямокутну будівлю із мармуру та дерева довжиною 105м та шириною 51 метр, обнесену з усіх сторін подвійною колонадою із 127 колон висотою 18 метрів.

Унікальним був сам спосіб побудови храму. Він був зведений на болотистому ґрунті. Незвичність вибору місця пояснювалася прагненням будівельників уникнути руйнування храму внаслідок частих землетрусів і пожеж. На думку архітектора Херсифрона, м'який болотистий ґрунт слугував амортизатором при землетрусах, а щоб запобігти осіданню величезної кам'яної будівлі, було вирішено заповнити котлован сумішшю деревного вугілля і вовни.

IІІ завдання. (спробуйте його розв’язати усно. Але спочатку пригадайте означення триг. функцій)

Куту α на одиничному колі відповідає точка М () . Чому дорівнюють значення sinα, cosα, tgα, ctgα?

IV чудо: Александрійський маяк.

Ще однією видатною спорудою античного світу був Александрійський маяк на острові Фарос в Єгипті (у гирлі (устье) річки Нил). Унікальність цієї споруди в тому, що це була перша в світі вежа із сигнальним вогнем.

Від землі до вершини цей маяк мав близько 180 м,  світло від відкритого вогнища з дров, що запалювали вночі на найвищій терасі фокусувалося за допомогою увігнутого дзеркала. Його  було видно на відстані 50-60 км. Всю споруду  увінчувала бронзова статуя покровителя морів Посейдона заввишки 8 м.

Маяк простояв майже тисячу років, але в 796 році його зруйнував землетрус.

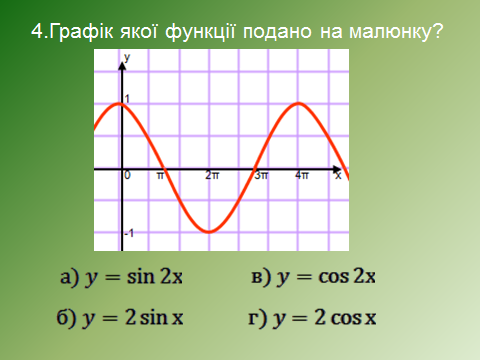
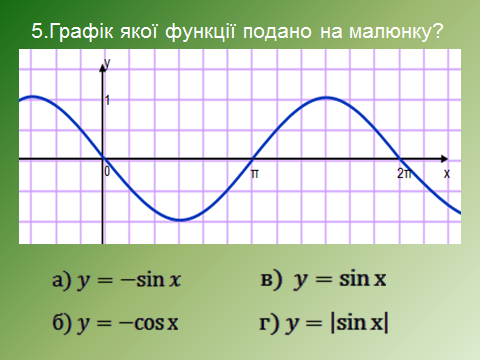
IV завдання.

 

 

 

 

 

 

 

 

 

 

 

 

Графік якої функції подано на малюнку?
Графік якої функції подано на малюнку?
Графік якої функції подано на малюнку?
Графік якої функції подано на малюнку?
Графік якої функції подано на малюнку?

 

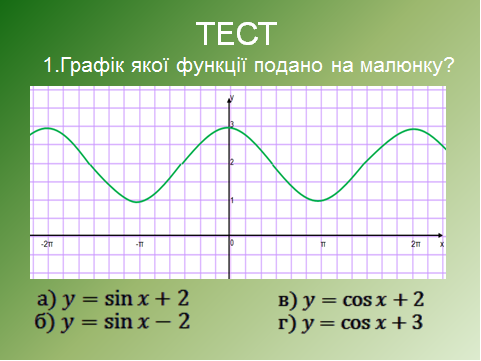
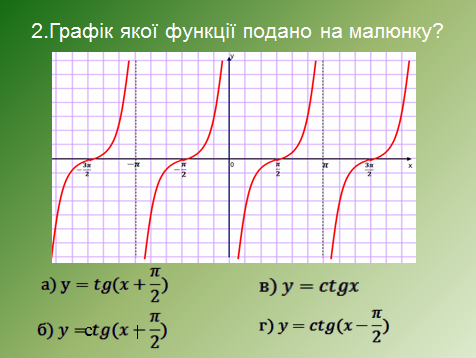
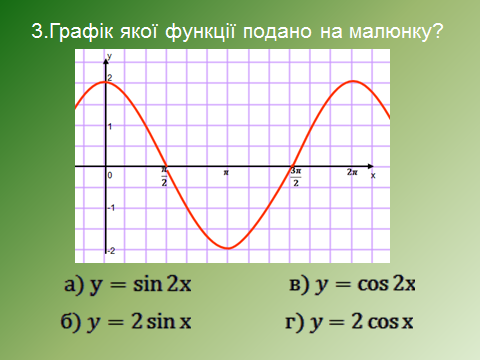
Відповіді: 1в, 2а, 3г, 4в, 5а.

V чудо:  Статуя Зевса Олімпійського 

Статуя Зевса — була споруджена на півострові Пелопоннес, у древньому місті Олімпія.

За переказами, саме тут Зевс вступив в боротьбу зі своїм батьком, кровожерливим і віроломним Кроном, який пожирав своїх дітей. Врятований матір'ю, змужнілий Зевс, переміг і примусив Крона відригнути своїх братів і сестер.

На честь цієї перемоги були встановлені олімпійські ігри, що уперше відбулися у 776 р. до н. е. Але десь через 300 років в Олімпії архітектор Лібон почав будувати храм, присвячений Зевсу, що став головною святинею міста.

Храм прикрашала статуя бога заввишки 12 м 40 см, богиня перемоги Ніка, яка стояла на долоні Зевса, була вища за звичайну людину.

Фігура Зевса була виконана з дерева, і на цю основу за допомогою бронзових і залізних цвяхів, спеціальних гачків кріпилися деталі з слонячої кістки і золота, очі в нього були з коштовних каменів.

 Мандрівники, які бачили Зевса в Олімпії, називають дивними поєднання в його лику владності і милосердя, мудрості і доброти.

V завдання.

Оскільки кращі атлети з усіх кінців Греції поспішали на свято в Олімпію – помірятися на честь Зевса силою, спритністю і швидкістю, то і ми спробуємо прийняти участь у так званих Олімпійських іграх. Пропоную естафету: на перших партах кожного ряду лежать кільця з завданнями на знаходження значень обернених тригонометричних функцій. За моєю командою ці кільця учні перших парт роздають п’ятьом учням свого ряду.  Ті швиденько усно або письмово розв’язують завдання, знаходять відповідь на кільці на дошці і приклеюють до нього. Яка команда першою складе сучасний олімпійський символ (прикріплюється на дошці за допомогою двостороннього скотчу), та і виявиться переможницею.

Початок естафети.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

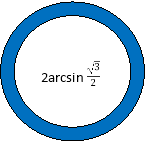
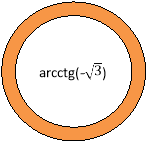
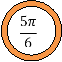
Відповіді до завдань:

Олімпійский символ – означає єдність п’яти континентів та зустріч спортсменів всього світу на Олімпійских іграх.

 

VІ чудо. Мавзолей в Галікарнасі 

Мавзолей — храм-гробниця і надгробний пам'ятник царя Мавсола, споруджений у середині IV століття до н. е. за наказом його дружини Артемісії III в Галікарнасі (Греція).

Мавсол був правителем міста Гелікарнас (після свого батька). З роками він набував все більшої могутності і задумувався про гробницю для себе і своєї цариці. На його думку, це повинна була бути надзвичайна гробниця. Мавсол мріяв про величний пам'ятник, який би нагадував світу про його багатство і могутність ще довго після його смерті.

Помер Мавсол до закінчення робіт над гробницею, але його вдова продовжувала керувати будівництвом до повного завершення, приблизно в 350 року до н. е.

Гробниця була названа мавзолеєм, на ім'я царя, і це слово стало означати всяку значну і величну гробницю.

 

Розв’язавши наступне завдання ви дізнаєтесь на якому острові знаходилось сьоме чудо античного світу.

Завдання: Спростіть вирази 1-5.  ВИРАЗИ ВІДПОВІДІ О)   C)  P)  O)  Д)

Заповніть таблицю:   № виразу   1 2 3 4 5   «Літера – відповідь»

VІІ чудо. Колос Родоський — величезна статуя грецького бога Сонця Геліоса, споруджена між 292 та 280 роками до н. е. на вході до гавані острова Родос (Греція). Статуя за час свого існування була найвищою в світі, висотою 70 ліктів (31,5 м). Геліос був не просто особливо шановним божеством на острові — він був його творцем.  Вважалося, що не маючи місця йому присвяченого, сонячний бог виніс острів на своїх руках з морської глибини.

 

Підведення підсумків.

VІ.  Підсумок уроку. Оцінювання учнів. (2 хв.)

        Учнівське резюме.

VІІ.  Домашнє завдання. (1 хв.)

Підручник «Алгебра і початки аналізу» М.І.Шкіль, с.157 №5(подати у градусній мірі кути, що виміряні у радіанах),№6(навпаки), №16(4 приклади на кілька дій: обчислити за таблицею «Значення тригонометричних функцій»).

ПРЕЗЕНТАЦІЯ