Методична розробка "Застосування методу площ до розв'язування геометричних задач"

ЗАСТОСУВАННЯ МЕТОДУ ПЛОЩ ДО РОЗВ'ЯЗУВАННЯ ГЕОМЕТРИЧНИХ ЗАДАЧ

 

Ця робота присвячена одному з методів розв’язання геометричних задач –методу площ. Використання методу площ значною мірою спрощує процес розв’язання деяких складних задач шкільного курсу геометрії, заощаджує час на екзаменах, допомагає розв’язувати олімпіадні задачі.

В підручнику геометрії 8, 9 класів А.Г. Мерзляка в задачах пропонується довести основні властивості площ, хоча системи задач, спрямованих на застосування властивостей площ,  немає.

Матеріали  можуть бути використані учнями як на уроках геометрії, так і при підготовці до ДПА у 9 класі, ЗНО у 11 класі, олімпіад та інших математичних конкурсів.

1. Основні властивості площ

 

Геометричну фігуру називають простою, якщо її можна розбити на скінчену кількість плоских трикутників. Для простих фігур площа – це додатна величина, числове значення якої має такі властивості: рівні фігури мають рівні площі; якщо фігура розбивається на частини, що є простими фігурами, то площа цієї фігури дорівнює сумі площ її частин; площа квадрата зі стороною, що дорівнює одиниці вимірювання, дорівнює одиниці. Фігури, які мають рівні площі, називаються рівновеликими.

Розглянемо кілька властивостей площ, які часто використовують при розв'язуванні планіметричних задач.

 

Властивість 1. Якщо два трикутника мають однакові висоти (або спільну висоту), то відношення їх площ дорівнює відношенню їх основ.

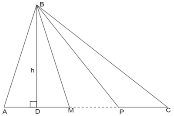Доведення. Нехай  у двох трикутників з основами і  рівні висоти . Розглянемо відношення площ цих трикутників: .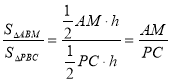

Рис. 1.1

Властивість 2. Якщо два трикутника мають однакові сторони (спільну сторону), то відношення їх площ дорівнює відношенню їх висот, які проведені до них.

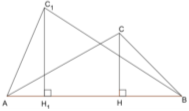Доведення. Розглянемо і . і їх висоти до спільної  сторони..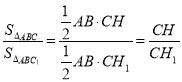

   Рис.1.2

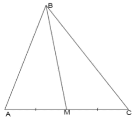Наслідок 1: Медіана трикутника діліть його на 2 рівновеликих  трикутника.

Доведення. За властивістю (3) : . За умовою , отже .

Властивість 3. Якщо два трикутника мають спільний кут, то їх площі відносяться як добуток сторін, утворюють цей кут.

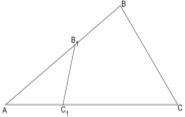Доведення: Розглянемо і зі спільним кутом A.  Використовуючи формулу площі трикутника  ,отримуємо:   

Рис. 1.4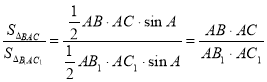                         

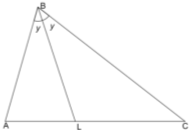Наслідок 2. Бісектриса кута трикутника ділить його на два трикутника, площі яких  відносяться як  сторони, які утворюють цей кут.

Доведення: .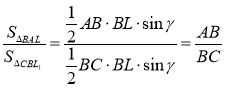

 

 Рис. 1.5

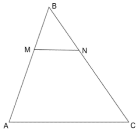Властивість 4. Відношення площ подібних трикутників (фігур) дорівнює  квадрату коефіцієнта подібності.

Доведення: Нехай в і , та  – спільний. Розглянемо відношення  площ подібних трикутників, отримуємо:

Рис. 1.6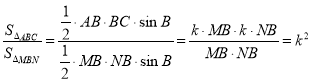              

 

2. Характеристика методу площ

 

Метод площ полягає в застосуванні різних властивостей площ фігур для складання співвідношень, які пов`язують відомі дані задачі і шукані елементи.

В методичній літературі  виділяють три типа задач, які розв’язуються за допомогою методу площ. Перший тип задач характеризується знаходженням площі фігури двома способами: складанням або рівняння, або системи рівнянь, тобто задача з геометричної перетворюється в алгебраїчну.

До другого типу відносяться задачі, при розв’язанні яких використовується властивість адитивності площі: якщо фігура розрізана на кілька частин, то її площа дорівнює сумі площі цих частин.

Задачі на застосування властивостей відношення площ, це задачі третього типу. Властивість відношення площ доцільно використовувати в тих випадках, коли мова йде безпосередньо про відношення площ або якихось відрізків.

 

3.  Застосування прийому, основаному на знаходженні площі фігури двома способами

 

Перерахуємо дії, які характеризують даний прийом:

1) складання виразу для площі фігури за умовою задачі;

2) складання виразу для площі фігури з використанням невідомого елемента;

3) складання рівності з отриманих виразів для отримання площі фігури;

4) розв'язування отриманого рівняння і знаходження невідомою в умові задачі величини .

Проаналізував багато задач з різних посібників й збірників, пропонуємо для розгляду найбільш типові і значущі задачі. Характерною особливістю таких задач є те, що площа може бути включена в умову або запитання задачі, а може і не фігурувати в них. Розглянемо приклади.

Задача 1. Знайти бісектрису прямого кута трикутника ABC, якщо катети AC=2, BC=3.

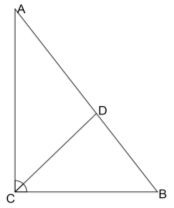Розв'язання 1. Розглянемо стандартне розв'язання цієї задачі.

За теоремою Піфагора знайдемо гіпотенузу трикутника:.

За властивістю бісектриси кута трикутнику :    ;  ;   .

   Рис. 3.1                 .  З за теоремою косинусів:  

.

Відповідь:.

Розв'язання 2. Застосуємо метод площ до цієї задачі. Підрахуємо площу   двома способами: ,

. 

. Отже .

Це рішення простіше і коротше.

 

Задача 2. Довести , що бісектриса кута трикутника ділить протилежну сторону трикутника на відрізки, пропорційні прилеглим сторонам кута (властивість бісектриси кута трикутника).

 

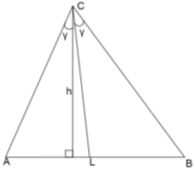Доведення. Нехай CL - бісектриса кута ACB. Позначимо h  висоту,  яка проведена до сторони AB. Підрахуємо площу трикутників ACL і BCL двома способами, отримуємо:

;    ;

Поділимо отримані рівності: , що і треба було довести.

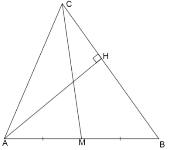Задача 3. В трикутнику ABC висота АН дорівнює медіані ВМ. Знайдіть кут МВС.

Розв'язання. Підрахуємо площу трикутника    двома способами: і . Прирівняємо вирази для площ:

  Рис. 3.3                            .

За умовою АН = ВМ, отже .

Відповідь:

4. Застосування властивості адитивності площі

 

Перерахуємо дії, які характеризують даний прийом:

1) розбиття фігури на частини з використанням умови задачі;

2) складання виразу для площ фігур, які отримали при розбитті (для цього варто використовувати як задані, так і шукані елементи задачі);

3) складання виразу для площі фігури як суми площ фігур, які її складають;

4) знаходження площі вихідної фігури, використовуючи дані задачі;

5)складання рівності отриманих виразів для площі фігури;

6) розв’язання отриманого рівняння і знаходження невідомої в задачі величини (або доведення заданої рівності).

Розглянемо приклади задач.

Задача 4. Площа паралелограма ABCD дорівнює S. Знайдіть площу чотирикутника AMCK, якщо точки M і K середини сторін BC і CD відповідно.

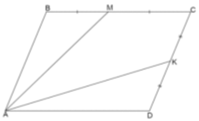Розв'язання.  Проведемо діагональ AC.  , а за наслідком 1 : і . Отже, .

Рис. 4.1                             Відповідь:

         

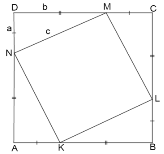Задача 5. Доведемо теорему Піфагора методом площ.

Доведення. Нехай дано прямокутний трикутник  з катетами a, b та гіпотенузою c. Треба довести, що . Побудуємо квадрат ABCD зі стороною .

Точки K, L, M, N на сторонах квадрата такі, що

 AK = BL = CM = DN = a,  KB = LC = MD = NA = b.

Рис. 4.2             KLMN квадрат зі стороною c і площею . З іншого боку,

  .Отже, .

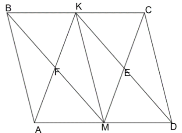Задача 6. Середини двох паралельних сторін паралелограма з'єднані з протилежними вершинами. Яка частина площі паралелограма обмежена проведеними відрізками?

 Розв'язання. Проведемо відрізок МК, отримуємо два паралелограма з однаковою площею. Діагоналі ділять кожний з них на чотири рівновеликих частини, отже  .

    Рис. 4.3             Відповідь: .

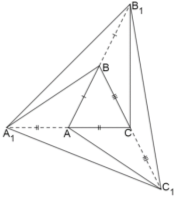Задача 7. На продовженні сторін трикутника АВС побудовані відрізки АА₁ =АС, ВВ₁=АВ, СС₁=ВС. Знайдіть , якщо .

Розв'язання. Виконаємо додаткову побудову і з'єднаємо точки А₁ і В, В₁ і С, С₁ і А.  Медіана трикутника ділить його на два рівновеликих трикутника,отже всі сім отриманих  трикутників мають рівні площі. Отже, .

 

  Рис. 4.4

 

5. Застосування прийому, основаного на відношенні площ і відповідних відрізків

 

Використання властивостей відношень відрізків і площ  при розв'язанні задач дозволяє виділити дії, які будуть входити в цей прийом:

1.               співвідношення шуканих відрізків з площею фігур,елементами яких вони є (або співвідношення площ шуканих фігур з відповідними відрізками), і застосування зазначених властивостей;
2.               знаходження відношення площ цих фігур (довжин відрізків).

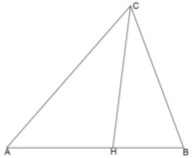Задача 9. У трикутнику АВС точка Н ділить сторону АВ в відношенні 2 : 3, вважаючи від вершини В. Знайдіть площу трикутника НВС, якщо площа трикутника АВС дорівнює 15.

Розв'язання. АВС і НВС мають спільний кут В, отже за властивістю 3:

. Отже,

.

     Рис. 5.1                     Відповідь: .

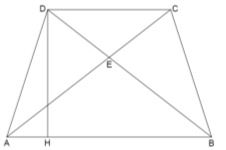
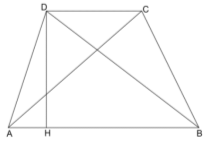Задача 10. У трапеції з основами АВ і СД  діагоналі перетинаються в точці Е. Знайдіть площу трикутника ВСЕ, якщо АВ = 30, СД = 24, АД = 3, кут ДАВ дорівнює .

Розв'язання. З АДН: . .

ДСЕ ВАЕ (за двома кутами). Отже,

  Рис. 5.2                . Трикутники ВСЕ і ВСД  мають однакову висоту, тому за властивістю 2 маємо: . Звідси, . 

Відповідь: .

Найбільш складний  по відношенню до розглянутих прийомів є тип задач, в розв'язанні яких необхідно одночасно використовувати і властивість адитивності площ, і властивість відношень площ.

Задача 11. На сторонах трикутника взято точки М, N, Р так, що

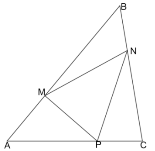АМ : МВ = ВN : СN = СР : АР = 1 : 2. Знайдіть площу трикутника АВС, якщо площа  МNР = 15 см.

Розв'язання. За умовою , . ABC  та MBN мають спільний кут В, отже, за властивістю 3: ,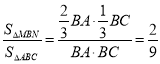

Рис. 5.3          Аналогічно ; . За властивістю адитивності:   . Отже,.

Відповідь: .

Задача 12. У трапеції з основами ВС і АД діагоналі перетинаються в точці О, Р – середина відрізку ОД. Знайдіть площу чотирикутника АВСР, якщо , АД = 6,  ВС = 2.

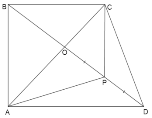Розв'язання. Нехай . ВСО DАО за двома кутами (ВСА=САД як внутрішні різносторонні при паралельних прямих ВС і АД, ВОС=АОД як                     вертикальні). Отже, . За властивістю 2:

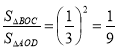; . Аналогічно, ., що означає, що . За властивістю 4:; ;. За властивістю адитивності:

. Так як за умовою ,.

 Відповідь: .

6. Використання методу площ до розв’язування завдань державної підсумкової атестації та  у та завдань ЗНО.

Був розглянутий збірник завдань ДПА авторського колективу А. Г. Мерзляк, В. Б. Полонський, М. С. Якір, рекомендований Міністерством освіти і науки України. Матеріали збірника на третину складаються з геометричних задач. З 50 запропонованих геометричних задач третя частина так чи інакше пов'язані із площами. Розглянемо декілька прикладів таких задач  третьої частини.

Задача 13. Висота рівнобедреного трикутника, яка проведена до основи, дорівнює 15, а до бічної сторони – 24. Знайдіть площу трикутника [10, варіант 24] .

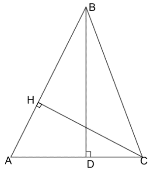Розв'язання . В трикутнику  ABC  AB = ВC, ВД = 15, h_a = 24 – висота, проведена до бічної сторони. Позначимо АВ = a , АС = b.

Підрахуємо площу трикутника двома способами:  і  .  Отримуємо рівняння:

Рис. 6.1                         ; .

З :;  ; ; .

.

Відповідь: .

Задача 14. В трикутник вписано коло, радіус якого 5. Знайти площу трикутника, якщо одна зі сторін трикутника точкою дотику діліться на відрізки 12 і 7,5. [10, варіант 10] .

 

 

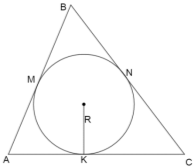Розв'язання. Нехай точки К, М, N – точки дотику кола зі сторонами АВС. За властивістю дотичних: АК = АМ = 12; МВ = ВN =7,5; СК = СN = x., з іншого боку, за

Рис. 6.2                     формулою Герона: .

Прирівняємо вирази для площ АВС і отримуємо рівняння:

;

;

.

.

Відповідь: .

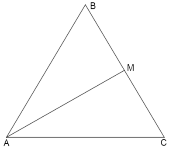Задача 15. Знайти площу АВС, якщо АВ = 26 см, АС = 30 см, а довжина медіани AM = 14 см [10, варіант 47]

Розв'язання. Добудуємо АВС до паралелограма АВСД, в якому М – середина АД. Тоді сторона АД = 28 см. Знайдемо площу АВД за формулою Герона:

, отже,

   Рис. 6.3                    . та

.

 

Відповідь: .

Задача 16. На сторонах трикутника АВС позначили точки Д і F так, що , а на стороні ВС – точки Р і М так, що . Знайдіть площу чотирикутника ДFРМ, якщо  [10, варіант 24]

 

 

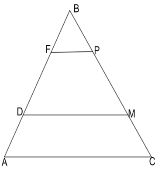Розв'язання. Ідея розв'язання задачі полягає в тому, що .  Оскільки , а – спільний, то АВС і  ДВМ подібні.

.     .

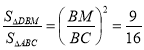Рис. 6.4             Аналогічно АВС і  FВР подібні, отже:

,    .

.

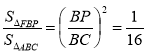Відповідь: .

Зазначимо, що задачі  14 і 15 розв'язані за допомогою прийому, заснованому на знаходженні площі фігури двома способами, а при розв’язуванні задач 15 і 16 потрібно одночасно використовувати властивість адитивності площ і властивість відношень площ.

У завданнях ЗНО також зустрічаються задачі, для розв’язку яких передбачається активна робота з площами. Такі завдання зустрічаються як у тестах, так і у завданнях на відповідність та в завданнях відкритої форми. Наведемо приклади таких задач.

Задача 17. Екрани телевізорів мають форму прямокутників, відповідні сторони яких пропорційні. Діагоналі екранів цих телевізорів дорівнюють відповідно 48 і 32 дюймів. Визначте у скільки разів відрізняються їх площі?

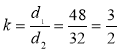Розв’язання. . Отже . За властивістю 4:.

Відповідь: 2,25.

 

 

Задача 18. У прямокутному трикутнику АВС точка М є серединою гіпотенузи АВ, довжина якої дорівнює 26 см. Точка О віддалена від вершин В і С на 15 см, а від сторони ВС – на см. З точки О на катет ВС опущено перпендикуляр ОК, точка К належить відрізку ОМ.

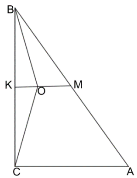1) Доведіть, що чотирикутник КМАС – трапеція.

2)  Визначте площу трапеції КМАС (ЗНО 2015).

Розв’язання: За умовою ВО = ОС, отже, ВОС – рівнобедрений, тому висота ОК є медіаною. К – середина ВС, М – середина АВ. Таким чином, КМ середня лінія . Отже, – трапеція.

  Рис. 6.5   

З ВКО:

 Точка М – середина АВ, тому .

З ВКM: KM=12 (5, 12, 13 – піфагорова трійка).

.

ВKM BCA; ;      ,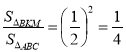

Тоді  

Відповідь: .

 

ВИСНОВКИ

 

Застосування методу площ є потужним інструментом для розв’язання планіметричних задач, який дає можливість учням обрати найбільш раціональний шлях до розв’язування геометричних задач.

Безумовно, що метод площ не є єдиним можливим способом розв’язування проаналізованих задач, однак його використання значною мірою спрощує процес розв’язування та заощаджує час на екзаменах.

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Кушнір І.А. Методи розв'язання задач з геометрії: кн. для вчителя / І.А. Кушнір. –К.: Абрис, 1994, – 464 с.
2. Готман Э.С. Задачи по планиметрии и методы их решения. Пособие для учащихся / Э.С. Готман. – М.: Просвещение, Учеб. лит., 1996. – 240 с.
3. Полонский В.Б. Учимся решать задачи по геометрии / В.Б. Полонский, Е.М. Рабинович, М.С. Якир.– Киев, 1996. – 256 с.
4. Новиков И.Д. Метод площадей / И.Д. Новиков // Квант. – 1971. – № 12. – С. 41–46.
5. Прасолов В.В. Используя площадь / В.В. Прасолов // Квант. – 1986. – № 5. – С. 16–19.
6. Мерзляк Г.А. Геометрія: підручник для 8 класу загальноосвітніх навчальних закладів / А.Г. Мерзляк , В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2016. – 224 с.
7. Шарыгин И.Ф. Учимся решать задачи  по геометрии / И.Ф. Шарыгин // Математика в школе. –1989. – №2. – С. 87–101.
8. Мерзляк А.Г. Геометрія: підручник для 9 класів загальноосвітніх навчальних закладів / А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2017. – 240 с.
9. Сарванова Ж.А. Формирование приемов, составляющих метод площадей, при обучении школьников решению геометрических задач / Ж.А. Савранова // Modern high technologies. – № 2. – 2016. – С. 380–384.
10. Мерзляк А.Г. Збірник завдань для державної підсумкової атестації з математики 9 кл. рівень / А.Г. Мерзляк  та ін. За ред. Н.І. Бурди. – К.: Центр навч.- мет. л-ри. 2018.