Розробка уроку для учнів 10 класу (студентів І курсу коледжу та училища) з математики на тему «Розв’язування тригонометричних рівнянь способами зведення до однієї тригонометричної функції, розкладання на множники».

 

Тема заняття:  Розв’язування тригонометричних рівнянь способами зведення до однієї тригонометричної функції, розкладання на множники.  

Навчальна мета заняття: перевірити рівень засвоєння попереднього навчального матеріалу, ознайомити з іншими способами розв’язування тригонометричних рівнянь,  формувати уміння і навички розв’язувати тригонометричні рівняння, відмінні від найпростіших, удосконалити уміння розв’язувати найпростіші тригонометричні рівняння.

Розвиваюча мета заняття: розвивати пізнавальний інтерес, уміння використовувати сформовані знання, навики і вміння, розвивати культуру мовлення, логічне мислення, пам'ять, вміння раціонально використовувати час та оволодівати принципами організації праці, допитливість, ініціативність.

Виховна мета заняття: виховувати працелюбність, прививати бажання мати якісні глибокі знання, виховувати зібраність, організованість, відповідальність, увагу, культуру міжособистісного спілкування, вміння співпрацювати в колективі. Тип заняття: комбінований

Форма проведення заняття: класно-урочна

Матеріально-технічне забезпечення та дидактичні засоби: таблиці, роздатковий матеріал, презентації, мультимедійне обладнання.

Хід заняття

I.                  Організаційно-психологічна частина.

II.               Перевірка домашнього завдання, повторення раніше вивченого матеріалу (активізація пізнавальної діяльності).

III.            Мотивація навчальної діяльності.

IV.            Повідомлення теми, мети, плану заняття. V.    Актуалізація опорних знань. VI.        Вивчення нового матеріалу.

VII.            Закріплення вивченого матеріалу.

VIII.         Підведення підсумків заняття. Рефлексія. IX. Домашнє завдання.

        

                                                  I.    Організаційно-психологічна частина

Привітання. 

1.            Перевірка присутності студентів на занятті.

2.            Перевірка санітарного стану кабінету.

3.            Призначення чергового.          ^{y =0,5x}

4.            Студенти отримують картки самоконтролю і викладач пояснює як треба їх заповнювати.  

 

 

Картка самоконтролю

Прізвище, ім’я_______________________

Група___________       Дата_____________

 

№ п/п	Види діяльності	Бали
1	Бліц-опитування ( по 1 балу)
2	Відповідність «Рівняння-корені» (по 0,5 бала за кожну відповідність)
3	«Чи знаєте Ви…?» (по 0,5 бала за формулу)
4	Розв’язування рівнянь:
	№4
	№5
	№6
	№7
5	Додаткові бали
	Оцінка

 

 

Викладач:

Французький математик, фізик, філософ Анрі Пуанкаре сказав: «Наука складається з фактів, як будинок із каменів, але набір фактів ще не наука, так само, як купа каміння ще не будинок». Ви знаєте вже багато фактів з тригонометрії, а саме графіки та властивості тригонометричних        функцій,     вивчили      велику кількість тригонометричних формул, знаєте як розв’язувати        найпростіші         тригонометричні рівняння і нашим сьогоднішнім завданням буде навчитись застосовувати ці факти (знання) при розв’язуванні більш складних тригонометричних рівнянь (іншими словами, маючи купу каміння будемо будувати будинок). 

        

II. Перевірка домашнього завдання, повторення раніше вивченого матеріалу (активізація пізнавальної діяльності) Викладач.

-         Що задавали додому? 

Шкіль М.І. та ін. Алгебра і початки аналізу 10 кл., р. 2, §12, с. 107-115 Вправа №57 (3, 5, 7, 9, 11), с. 115.

-         Чи виникли труднощі під час виконання домашнього завдання?

Перевірку теоретичного матеріалу виконаємо із застосуванням бліцопитування.

Бліц-опитування (усна перевірка знань, фронтальна робота)

На екрані буде з’являтись запитання – студенти дають відповідь. Хто перший підняв руку, той має право відповідати. За кожну правильну відповідь нараховується 1 бал, який вписуєте до картки самоконтролю. Доповнення також оцінюється. Увага на екран!

Запитання для студентів:

1.     Які рівняння називаються тригонометричними?

Рівняння, у яких невідоме (змінна) входить лише під знак тригонометричної функції.

2.     Які рівняння називаються найпростішими?

Рівняння виду sinx a,cosx a tgx, a ctgx,    a   

3.     При якому значенні a тригонометричні рівняння sinx a,cosx a мають розв’язки?

Якщо a  1;1

4.     При якому значенні a тригонометричні рівняння tgx a ctgx, a мають розв’язки?

При будь-якому a з множин дійсних чисел, a  ; 5. Що таке arcsina?

Арксинусом числа a називається таке число (кут) з проміжку ^_^2 2; ^_ , синус

якого дорівнює a 6. Що таке arccosa?

Арккосинусом числа a називається таке число (кут) з проміжку 0;, косинус якого дорівнює a7. Що таке arctga?

Арктангенсом числа a називається таке число (кут) з проміжку ^_^2 2; ^_, синус

якого дорівнює a 8. Що таке arcctga ?

Арккотангенсом числа a називається таке число (кут) з проміжку 0;, котангенс якого дорівнює a

9.                 Чому дорівнює arcsina? arcsin a arcsina

10.            Чому дорівнює arccos(a)? arccos(  a)  arccosa

11.            Чому дорівнює arctg(a)? arctg( a) arctga

12.            Чому дорівнює arcctg(a)? arcctg(  a)  arcctga

13.            Яка особливість розв’язку тригонометричних рівнянь?

Як правило або зовсім не мають розв’язків або мають їх безліч.

14.            Внаслідок якої властивості  тригонометричних функцій тригонометричні рівняння мають безліч розв’язків?

Періодичності Встановіть відповідність «Рівняння - корені» 

(групова, письмова робота)

Викладач нагадує студентам, що на минулому занятті були розглянути види найпростіших тригонометричних рівнянь та формули для отримання їх коренів (розв’язки), які вони повинні були вивчити на сьогодні. Для перевірки знань пропонується встановити відповідність між рівняннями і коренями.

Для виконання цього завдання необхідно об’єднатися в групи по 4 студента. Кожна група отримує заздалегідь підготовлений один бланк, де вони вписують свої прізвища. Після колективного обговорення записують відповіді. Представник кожної групи студентів передає бланк із відповідями викладачу. Викладач висвічує правильні відповіді на екрані і оголошує результати (перевірка за допомогою студентів).  Увага на екран!

        

Вправа «Чи знаєте Ви…?» (усна, фронтальна робота)

Наступне завдання дозволить перевірити чи знають студенти тригонометричні формули Знання цих формул знадобляться під час вивчення нового матеріалу. Увага на екран!

 

Викладач робить висновок про рівень засвоєння навчального матеріалу, називає прізвища активних студентів. 

 

ІІІ. Мотивація навчальної діяльності

 

Студентам пропонується переглянути презентацію «Тригонометрія навколо нас». Підбір матеріалу до презентації, створення і проведення презентації виконує студент (випереджальне завдання). 

Викладач акцентує увагу студентів на широкому застосуванні тригонометрії в науці і техніці, в навколишньому середовищі і робить висновок про актуальність теми розв’язування тригонометричних рівнянь.

 

IV.          Повідомлення теми, мети, плану заняття

На сьогоднішньому і наступних заняттях ми розглянемо різні способи розв’язування тригонометричних рівнянь, які відрізняються від найпростіших. Сьогодні ви познайомитесь з такими способами розв’язування тригонометричних рівнянь як зведення до однієї тригонометричної функції і розкладання на множники.

Викладач оголошує тему, мету, план заняття, студенти записують в зошити тему, план заняття. 

 

V.              Актуалізація опорних знань.

Для розуміння наступного потрібно розуміння попереднього. Дуже ефективною для проведення повтору є вправа «Асоціативний кущ».

        

Викладач пропонує студентам скласти «асоціативний кущ», ключовим словом (поняття, термін) якого є «рівняння». Студенти мають згадати все, що виникає в пам’яті стосовно          цього          слова.          Очікувані відповіді студентів: алгебраїчне, квадратне, дробове,          тригонометричне найпростіше, неповне,          повне,         невідоме,    корені, розв’язування,          дискримінант,      коефіцієнт, скласти, теорема Вієта, лінійні, квадратні, дробові.

                    Настанова     викладача     (осмислення     й     поглиблення     особливостей

розвязування тригонометричних рівнянь)

1.           Особливістю розв’язування тригонометричних рівнянь є те, що загальних методів, способу не існує.

2.           Що вони (рівняння) або зовсім не мають розв’язків, або мають безліч, внаслідок періодичності (про що ми вже згадували).

3.           Існує дуже багато тригонометричних рівнянь, і самих найрізноманітніших, тому і способів розв’язування існує багато. Ми будемо намагатись розробити і сформулювати загальні (універсальні) орієнтири (рекомендації) розв’язування тригонометричних рівнянь.  

VI. Вивчення нового матеріалу

Згідно плану заняття відбувається вивчення нового матеріалу. 

Увага на екран!

Викладач Перед вами тригонометричні рівняння.

1.      sin ^x _1

4

2. 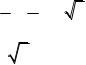     2cos5 3x 3

3.      tg3x 3       0

4.      tg² x3tgx 4       0

5.      2cosx 2    5sin² x

6.      cos2xsinx0

7.      sin4xsin2x0

Назвіть найпростіші

Очікувані відповіді: 1, 2, 3.

Такі рівняння ви вмієте розв’язувати за відповідними формулами. Інші рівняння не є найпростішими. Питання: Як розв’язувати ці рівняння?  Розв’язування рівняння відбувається під керівництвом викладача.

Запис розв’язку рівняння

Розв’язання	Коментар
tg2 x3tgx 4   0	Помічаємо, що до складу рівняння входить лише одна функція тангенс одного аргументу х.
tgx t	Отже, зручно ввести нову змінну tgx t.
t2   3t 4 0	Записати рівняння, використовуючи нову змінну.
t1 4, t2 1	Розв’язати            отримане            квадратне (алгебраїчне) рівняння
1.                 При t1 4, маємо tgx4, тоді за формулою коренів рівняння tgxa x1 arctg4k, k Z 2.                 При   t2 1 маємо tgx1, тоді x2 arctg( 1) k,  x2 arctg1k,  x2   k, k Z 4	Повернутися до початкової змінної (виконати обернену заміну) та розв’язати отримані найпростіші тригонометричні рівняння. Рівняння має коренів при будьякому значенні t, оскільки E tgx( ); .  Врахувати, що     арктангенс -        непарна функція.
Відповідь:         x1 arctg4k, x2   k, k Z 4	Записати відповідь, враховуючи, що значення arctg4 існує, але вираз не спрощується.

Аналізуємо вигляд наступного рівняння: 2cosx 2     5sin² x

Викладач: Чи однакові аргументи у рівнянні? Так

Тоді наступне запитання Чи потрібно зводити рівняння до однієї функції? Так Яким чином це зробити?

Йде колективне обговорення, після якого студент біля дошки розв’язує рівняння при необхідності із коментарем або за під керівництвом викладача.

Запис розв’язку рівняння

_{Наступне рівняння. Аналізуємо його вигляд:} cos2xsinx0

Викладач: Чи однакові аргументи у рівнянні? Ні   Чи потрібно зводити рівняння до однієї функції? Так Яким чином це зробити?

Спробуємо зробити так, щоб у рівняння входила одна і та сама функція одного й того самого аргументу.

Йде колективне обговорення, після якого викладач і студент біля дошки розв’язує рівняння при необхідності із коментарем або за під керівництвом викладача.

Запис розв’язку рівняння

Викладач:. Аналізуємо вигляд наступного рівняння: sin4xsin2x0

Чи однакові аргументи у рівнянні? Ні  

Чи потрібно буде зводити до однієї функції, подивимось

Йде колективне обговорення. Запис розв’язку рівняння

Можна запропонувати інший спосіб розкласти ліву частину рівняння на множники:

1.     Застосувати формулу перетворення суми (різниці) тригонометричних функцій у добуток.

2.     Добуток дорівнює нулю, якщо хоч один із множників дорівнює нулю.

3.     Розв’язати найпростіше тригонометричне рівняння.

4.     Записати відповідь

Яким би складним не було тригонометричне рівняння, розв’язати ми його зможемо за умови дотримання певних орієнтирів (рекомендацій). Давайте їх сформулюємо і запишемо:

1.     Звести тригонометричні функції до одного аргументу.

2.     Звести тригонометричне рівняння до однієї функції

3.     В інших випадках переносимо всі члени рівняння в ліву частину і намагаємось розкласти на множники.

VII. Підведення підсумків заняття. Рефлексія

Викладач підводить підсумки заняття, студенти підсумовують кількість набраних балів, записаних в картках      самоконтролю      і викладач оголошує результати. На сьогоднішньому занятті Ви зуміли застосувати свої знання на      практиці,    обмінялися знаннями,      оцінили      свою діяльність    на      занятті        та отримали      можливість

замислитись над підвищенням якості  роботи, оцінивши свій рейтинг. Щоб досягти успіху треба працювати, вчитися і не боятися труднощів. 

VIII. Домашнє завдання