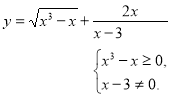МЕТОДИЧНІ РЕКОМЕНДАЦІЇ щодо використання програмного забезпечення при вивченні теми «Функції, їхні властивості і графіки» з предмету «Математика» для студентів базової середньої о

Міністерство освіти і науки України

Кропивницький коледж харчування та торгівлі

 

 

 

 

 

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

щодо використання програмного забезпечення при вивченні теми «Функції, їхні властивості і графіки»

 з предмету «Математика»

для студентів базової середньої освіти

спеціальності «Підприємництво, торгівля та біржова діяльність»

 

 

 

Склала викладач: Чорна А.А.

 

 

 

 

 

Розглянуто на засіданні циклової комісії

обліково-економічних дисциплін

Протокол №___

від «__» ______2018р.

Голова циклової комісії _____І.М. Щербак

ЦІЛІ ТА ЗАВДАННЯ ТЕМИ

Метою вивчення теми «Функції, їхні властивості і графіки» є систематизація та розширення знань студентів про числа, степені, корені, узагальнити знання про різновиди функцій, розвинути навички «читання» і побудови графіків функцій.

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

Методичні рекомендації з математики використовуються  під час вивчення теми  «Елементарне дослідження функції», а також вивчення даної теми поєднується з вивчення теми «Micrоsoft Office – Табличний процесор Microsoft Excel» з предмету «Інформатика» . Матеріал, що розглядається в даній темі, не є зовсім новим для студентів, але він дає можливість розширити та поглибити знання студентів про функцію, зокрема вивчити її властивості, навчитися використовувати властивості функцій для побудови їх графіків, розв’язувати рівняння та нерівності.

Під час  проведення заняття слід мати на увазі, що тема має пропедевтичний характер. Дослідження функцій розглядатиметься знову після вивчення похідної в ІІ семестрі. Тому тут прослідковується випереджаюче навчання.

Студентам доречно повідомити, що властивості функцій є базою для розгляду питання щодо розв’язування рівнянь і нерівностей. Дійсно, розв’язати рівняння означає знайти нулі відповідної функції, а знайти проміжки знакосталості – розв’язати відповідну нерівність.( дані теми будуть вивчати також на І курсі в І семестрі)

Необхідно також нагадати студентам, що з деякими властивостями функцій вони ознайомилися в попередніх класах. ( 9й класс школи).  Це такі властивості, як нулі функції, знакосталість, зростання та спадання функції. Проте вивченого недостатньо для того, щоб розв’язувати деякі прикладні задачі (наприклад, будувати графіки функцій). Тому першочерговим постає питання щодо повторення відомих властивостей, а також розгляд інших властивостей функцій. Вивчення цих властивостей, формування вміння застосовувати їх до розв’язування задач – основна дидактична мета цієї теми.

Повторення елементарних перетворень графіка функції сприяє кращому розумінню і запам’ятовуванню того, які саме перетворення необхідно виконати, щоб уникнути помилок, яких   часто припускаються студенти, особливо якщо мова йде про паралельне перенесення вздовж різних координатних осей.

Слід відмітити, що дуже важливими моментами на занятті є використання мультимедійного проектора. Протягом заняття учні при розв’язуванні вправ використовують велику кількість графіків функцій, чого неможливо було б зробити без використання комп’ютера. Так, накресливши ескіз графіка функції студенти, зберігаючи ще цікавість до цього графіка, можуть швидко побачити справжній графік цієї функції  у спроектованій на дошку системі координат.

Розглядаючи  функції, часто доводиться розв’язувати не тільки пряму задачу про знаходження значення функції за відомим значенням аргументу, а й обернену задачу про знаходження аргументу за відомим значенням функції. Програма передбачає ознайомлювальний характер вивчення теми про обернену функцію, але даний матеріал має широке застосування, наприклад, під час вивчення обернених тригонометричних функцій, показникової та логарифмічної функцій, що будуть вивчатись пізніше.

Завдання на встановлення властивостей функцій, обернених до заданих, та побудову графіків є досить складними, оскільки їх розв’язування передбачає вільне володіння знаннями про види елементарних функцій, їх властивості та графіки, оволодіння вміннями виконувати геометричні перетворення графіків елементарних функцій, будувати фігури, симетричні відносно прямої. Тому рівень складності завдань викладач обирає залежно від рівня підготовленості студентів, не занижуючи вимог, але водночас створюючи ситуацію успіху.

Як приклад, можна взяти будь-яку функцію і побудувати графік функції, оберненої до даної. Під час такої роботи в студентів розвивається уява, інтуїція, логічне мислення, вміння будувати графік, симетричний даному відносно прямої у=х. Побудувавши ці графіки (зазвичай студенти трохи допускають неточності), викладач в цю ж систему координат проектує правильні графіки. Така робота у дітей збуджує цікавість до предмету, розвиває навички точно будувати графіки.

 

 

 

 

 

 

 

 Вивчення даної теми, складається з лекції, та практичних занять. Лекція з даної теми складається з таких питань:  (додаток 1 з повним змістом лекції)

1. Поняття функції, способи її задання
2. Найпростіші властивості функцій
3. Поняття оберненої функції
4. Перетворення графіків функцій

Функцію можна задати за допомогою таблиці, графіка, формули. Найчастіше функцію задають формулою, яка дає можливість одержати значення залежної змінної у, підставивши конкретне значення аргументу х.

Областю визначення функції у=f(х), яка задана формулою, називають множину тих значень, яких може набувати х, тобто таких х, за яких формула має зміст (усі дії, указані формулою, можна виконати).

Дати поняття про функції та їх області визначення доцільно на конкретних прикладах. Наприклад:

1.     Якщо функція є многочленом 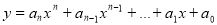 , то 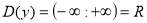(наприклад,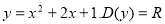
2.     Якщо функція має вигляд 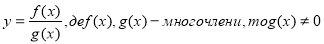(наприклад, 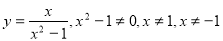, Отже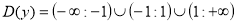
3.     Якщо функція має вигляд: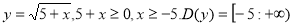

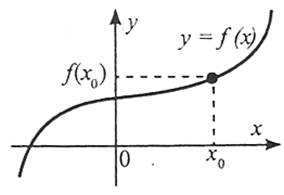
Графіком функції  називають множину всіх точок площини з координатами , де перша координата «пробігає» всю область визначення функції , а друга – це відповідні значення функції у точці х.

Повторення всіх графіків функції та способів їх побудови представлено як презентацію, в якій розглядаються усі графіки які вже вивчались, їх способи задання, способи побудови та їх графіки. ( Додаток 2)

Далі розглядаємо всі властивості функцій та їх графіків. Всі матеріали представлені в лекції. А також на практичному занятті розглядаються властивості не тільки на прикладі, і на дошці а й за допомогою проектора студенти розглядають і відповідають на питання і завдання с презентації (Додаток 3).

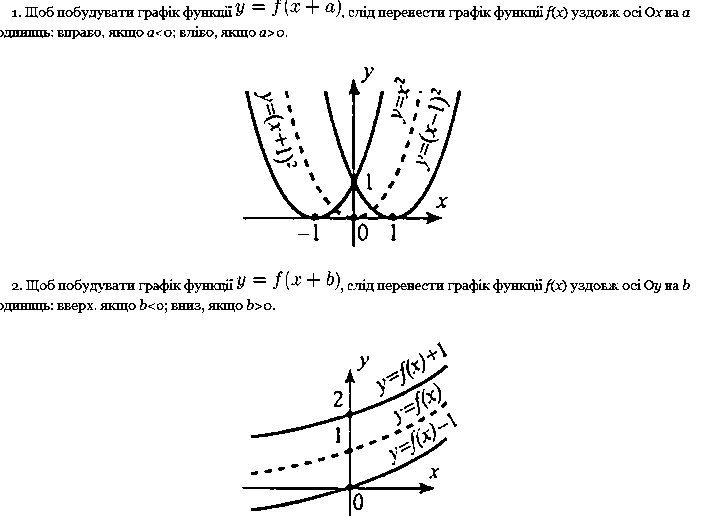 Перетворення графіків функцій розглядається на прикладах.

 

 

 

 

 

 

 

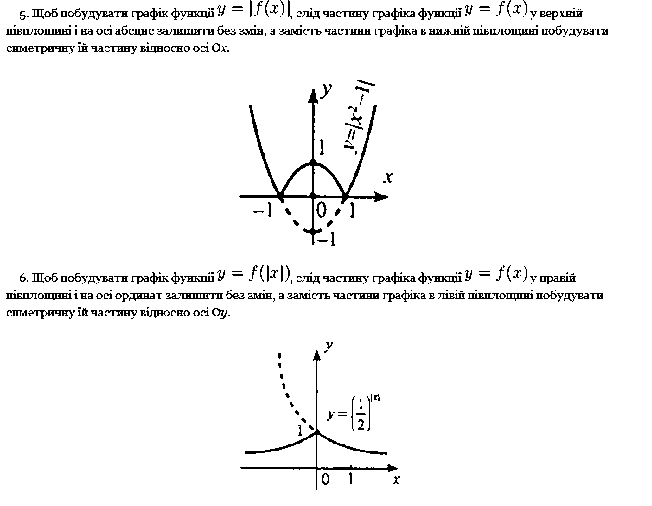
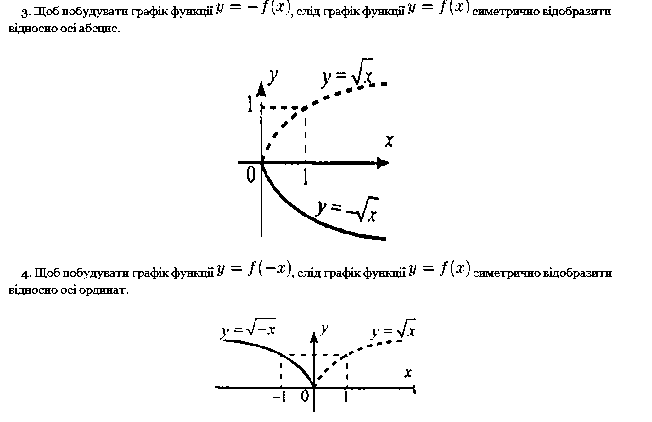
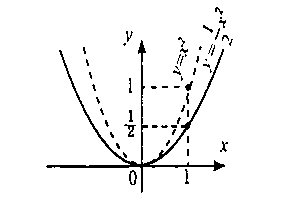
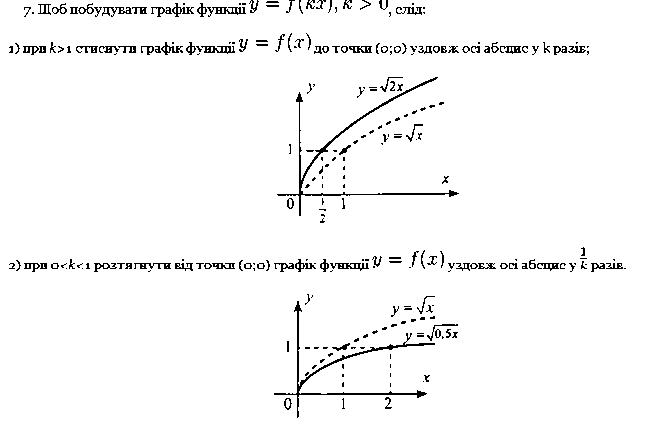
Вивчення теми про функції доцільно розглядати наочно, як в презентаціях, так і за допомогою таких програм як Гран2Д, а також за допомогою програми офіса  - табличний процесор Microsoft Excel, в якій можливі всі перетворення і побудова графіків функцій.

 Введення тексту і чисел. Введення даних здійснюють безпосередньо в поточний осередок або в рядок формул, розташований у верхній частині вікна програми безпосередньо під панелями інструментів (рис.1 ).

 

 

 

 

 

 

 

 

 

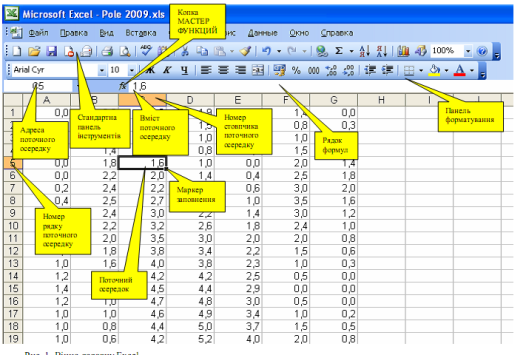
Рис.1 Вікно редактора Microsoft Excel

Формули. Обчислення в таблицях програми Excel здійснюються за допомогою формул. Формула може містити числові константи, посилання на осередки і функції Excel, сполучені знаками математичних операцій. Дужки дозволяють змінювати стандартний порядок виконання дій.

Правило використання формул в програмі Excel полягає в тому, що, якщо значення осередку залежить від інших елементів таблиці, завжди потрібно використати формулу, навіть якщо операцію легко можна виконати. Це гарантує, що подальше редагування таблиці не порушить її цілісності і правильності обчислень, що виробляються в ній. Формула може містити посилання, тобто адреси осередків, вміст яких використовується в обчисленнях. Це означає, що результат обчислення формули залежить від числа, що знаходиться в іншому осередку. Осередок, що містить формулу, таким чином, є залежним. Значення, що відображається в осередку з формулою, перераховується при зміні значення осередку, на який вказує посилання. Посилання на середок можна задати різними способами. По-перше, адресу осередку можна ввести вручну.Інший спосіб складається з кліку по потрібному осередку або виборі діапазону, адресу якого потрібно ввести. Осередок або діапазон 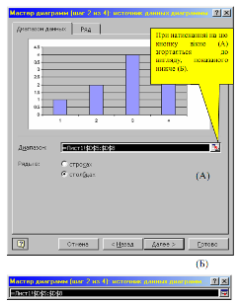при цьому виділяються пунктирною рамкою. Всі діалогові вікна програми Excel, які вимагають вказівки номерів або діапазонів осередків, містять кнопки, приєднані до відповідних полів. При натисненні на такій кнопці діалогове вікно згортається до мінімально можливого розміру, що полегшує вибір потрібного осередку (діапазону) за допомогою натиснення або простягання (рис. 2). При натисканняі на цю кнопку вікно (А) згортається до вигляду, показанного нижче (Б).

Рис. 2

Стандартні функції використовуються в програмі Excel тільки в формулах. Виклик функції складається з вказівки в формулі імені функції, після якої в дужках вказується список параметрів. Окремі параметри розділяються в списку крапкою з комою. Як параметр може використовуватися число, адреса осередку або довільне вираження, для обчислення якого також можуть використовуватися функції.

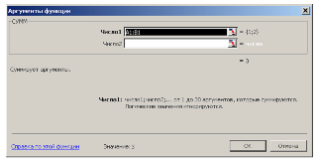Діалогове вікно АРГУМЕНТЫ ФУНКЦИИ. Якщо почати введення формули натисненням на початковій кнопці в рядку формул, з'явиться діалогове вікно АРГУМЕНТЫ ФУНКЦИИ (рис. 3).

Рис. 3

Вона містить значення, яке вийде, якщо негайно закінчити введення формули. У лівій частині рядка формул, де раніше розташовувався номер поточного осередку, тепер з'являється список функцій, що розкривається. Він містить десять функцій, які використовувалися останніми, а також пункт ДРУГИЕ ФУНКЦИИ ( рис.3 )

Використання майстра функцій. При виборі пункту ДРУГИЕ ФУНКЦИИ запускається МАСТЕР ФУНКЦИЙ, що полегшує вибір потрібної функції. У списку КАТЕГОРИЯ вибирається категорія, до якої відноситься функція, серед яких є Повний алфавітний перелік, тоді нижче у списку ВЫБЕРИТЕ ФУНКЦИЮ з'явиться перелік функцій даної категорії. Після виділення потрібної і натискання кнопки ОК, ім'я функції занесеться в

рядок формул разом з дужками, що обмежують список параметрів. Текстовий курсор встановлюється між цими дужками.

Введення параметрів функції. У вікні вікно АРГУМЕНТЫ відображаються поля, призначені для введення параметрів. Якщо назва параметра вказана напівжирним шрифтом, параметр є обов'язковим і відповідне поле повинне бути заповнено. Параметри, назви яких приводяться звичайним шрифтом, можна опускати. У нижній частині палітри приводиться короткий опис функції, а також призначення змінного параметра. Параметри можна вводити безпосередньо в рядок формул або в поля палітри формул, а якщо вони є посиланнями - вибирати на робочому листі. Якщо параметр заданий, в палітрі формул вказується його значення, а для опущених параметрів значення, прийняті за умовчанням. Тут можна також побачити значення функції, обчислене при заданих значеннях параметрів.

Правила обчислення формул, що містять функції, не відрізняються від правил обчислення більш простих формул. Посилання на осередки, які використовуються як параметри функції, також можуть бути відносними або абсолютними, що враховується при копіюванні формул методом автозаповнення.

Для визначення виду залежності між величинами у прямокутній декартовій системі координат необхідно побудувати точки за даними значеннями наведеними у таблиці.

 

 

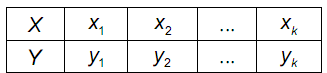
Ці точки незначно відхиляються від точок деякої лінії. Побудова виконується у середовищі Microsoft Excel засобом «Мастер диаграмм».

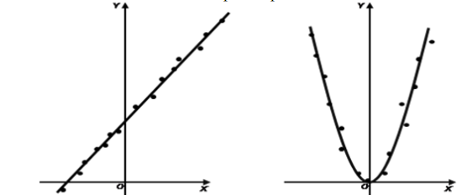
За виглядом графіку робиться припущення про вид залежності, наприклад,

Наприклад, Квадратична функція має вигляд: 

Для знаходження коефіцієнтів залежності, тобто , cкладають й вирішують систему рівнянь, попередні результати розрахунків для якої зручно оформляти у вигляді таблиці, значення якої обчислюють теж у середовищі Microsoft Excel засобом «Мастер функций».

Наприклад, нехай у результаті експерименту (деяких вимірів) отримані дискретні значення змінної x та залежної від неї змінної y. Ці данні подані у

таблиці:

X	-2,1	-1,1	0	1,1	2,1	2,6
Y	4,4	0,3	-2	-1,8	0,2	2,1

 

Визначення виду залежності між величинами X й Yзасобом «Мастер диаграмм» середовища Microsoft Excel представлено на малюнку .

 

 

 

 

 

 

 

 

 

 

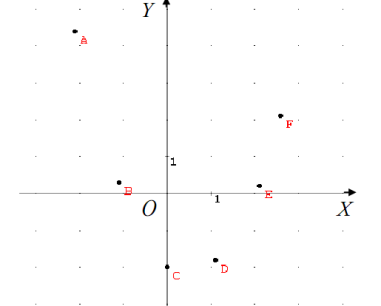
 Рис.4

 

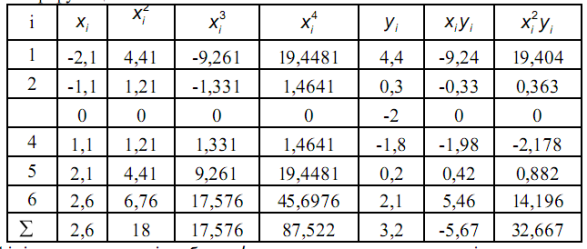За даними таблиці виконуються проміжні розрахунки у середовищі Microsoft Excel засобом «Мастер функций». 

 

 

 

 

 

 

 

 

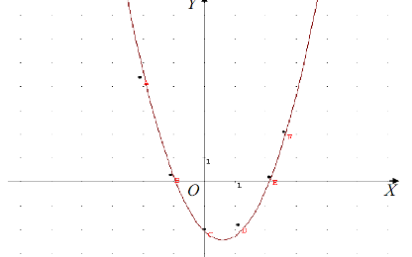
Задача вважається розв’язаною якщо знайдено аналітичний вираз залежності та побудовано її графік. Графік цієї залежності подано на малюнку 5.

Рис. 5

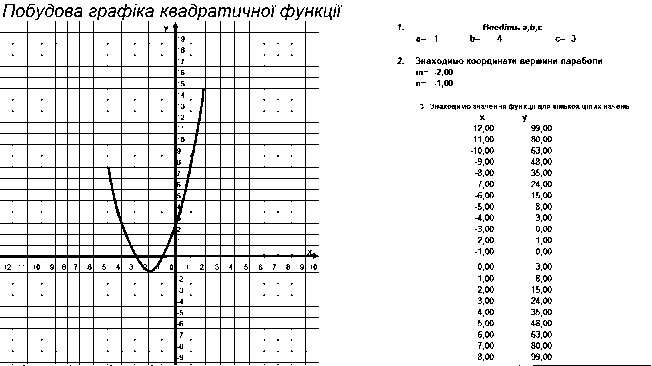
На прикладі розглянемо побудову графіка квадратичної функції в програмі табличного процесора Microsoft Excel.

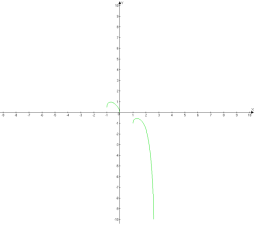Практичні завдання: Знайти область визначення і побудувати графіки функцій в Microsoft Excel.

1.  
2. 

 

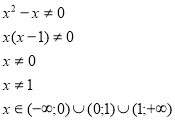
В кінці вивчення теми розроблено різнорівневі завдання практичні в зошиті, а також творчі завдання в програмі Microsoft Excel. А також експрес-тести на перевірку знань і умінь студентів, щодо основних видів функцій, їхніх властивостей та які саме графіки до них є, а також як по графіку функції визначати властивості функцій (нулі функції, область визначення та множину значень функції, парність і непарність функції, періодичність, проміжки зростання і спадання функції).

Приклади експрес –тестів, усних вправ, представлені в Додатку 4. 

В кінці побудови графіків квадратичної функції в тій же програмі Microsoft Excel представлено тест на визначення рівня засвоєння знань. (додаток 5)