Відділ освіти, сім`ї, молоді та спорту Семенівської селищної ради Полтавської області

Семенівський навчально-виховний комплекс №1

імені М. М. Хорунжого

               

               

 

                                                        

 

 

                           Л. М. Власюк

 

 

 

МЕТОДИЧНИЙ ПОСІБНИК:

 

Задачі з параметрами, пов`язані з дослідженням квадратичної функції

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СЕМЕНІВКА – 2020

ВЛАСЮК ЛАРИСА МИХАЙЛІВНА

 

Учитель математики Семенівського навчально-виховного комплексу № 1 імені                           М. М. Хорунжого, стаж роботи за фахом – 23 роки, учитель-методист вищої кваліфікаційної категорії.

 

Анотація

Розв’язання задач з модулем, що містять параметр, спирається на знання властивостей квадратичної функції, графічних побудов та перетворення геометричного місця точок на координатній площині.

Робота містить методично-теоретичну розробку даної теми, опорні конспекти для полегшення засвоєння та повторення матеріалу, графічні ілюстрації. Це сприяє розвитку в учнів абстрактного та алгоритмічного видів мислення; логічного мислення розгалуження; наочно-образного мислення, пошукової евристичної діяльності.

Матеріал може бути використаний у підготовці до олімпіад, конкурсів, зовнішнього незалежного оцінювання, а також для поглиблення знань з теми «Квадратична функція», для закріплення й підвищення рівня знань з математики.

Даний матеріал апробований у Семенівському навчально-виховному комплексі №1 імені М. М. Хорунжого.

Рецензенти: Вайло С. А. – методист методичного кабінету відділу освіти, сім`ї, молоді та спорту Семенівської селищної ради.

 Федоренко А. Г. – заступник директора з навчально-виховної роботи Семенівського навчально-виховного комплексу №1 імені М. М. Хорунжого.

ЗМІСТ

 

	Вступ...................................................................................................	4
1.	Розташування коренів квадратного тричлена на числовій осі (необхідні і достатні умови).............................................................	5
2.	Узагальнення теоретичних міркувань у вигляді опорних таблиць...............................................................................................	9
3.	Приклади розв`язання задач з допомогою міркувань (окремі випадки) ...........................................................................................	12
4.	Нерівності з параметрами, пов`язані з дослідженням квадратичної функції........................................................................	13
5.	Типові задачі на дослідження квадратичної функції з параметрами........................................................................................	17
6.	Модуль і параметр у задачах на дослідження квадратичної функції. ...............................................................................................	19
7.	Приклади задач, що приводять до дослідження квадратичної функції. ...............................................................................................	21
	Висновки.............................................................................................	23
	Список використаної літератури......................................................	24

Вступ

 

Задачі з параметрами традиційно входять до складу завдань ЗНО, математичних конкурсів та олімпіад різних рівнів і мають на меті перевірку логічного мислення учнів. У більшості школярів та майбутніх абітурієнтів розв`язання таких задач викликає страх не тому, що вони не здатні логічно мислити, а тому, що у звичайній школі мало уваги приділяється завданням, що у своєму розв`язанні вимагають мислення розгалуження, вміння прозоро й лаконічно записувати розв`язання, а задачі з параметрами, як правило, взагалі ігноруються.

Об`єктом дослідження даної методичної роботи є задачі з параметрами.

За мету я ставлю формування предметних компетентностей: розв`язування параметричних задач, поступове адаптування учнів до завдань з параметрами; формування ключових компетентностей: абстрактного та алгоритмічного видів  мислення, наочно-образного мислення (при використанні геометричної інтерпретації), пошукової евристичної діяльності (при пошуку раціональних способів розв`язування),  формування елементарних навичок роботи з параметрами.

Опорні конспекти допоможуть повторити та узагальнити певний навчальний матеріал, полегшать його залучення до розв`язування задач.

1. Розташування коренів квадратного тричлена на числовій осі (необхідні і достатні умови).

Для розв`язування багатьох задач з параметрами дуже важливим є знання властивостей квадратичної функції і залежності цих властивостей від можливих співвідношень між коефіцієнтами.

Нехай нам задане квадратне рівняння

 , – квадратична функція.

Введемо позначення:

a, b, c – коефіцієнти квадратичної функції; 

f(m) – значення функції в точці ;

 – дискримінант;

   – абсциса вершини параболи;

   – ордината вершини параболи;

– менший корінь рівняння;

– більший корінь рівняння;

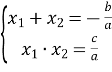– теорема Вієта.

 

Дослідження знака дискримінанта дозволяє встановити, дійсні чи комплексні корені квадратного тричлена. Однак для цілого ряду задач треба ще встановити, як розташовані на числовій осі дійсні корені квадратного тричлена відносно яких – небудь фіксованих точок числової осі.

Це можна зробити за допомогою наступних теорем:

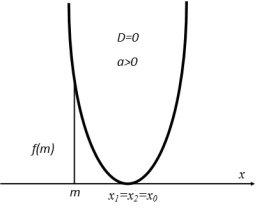
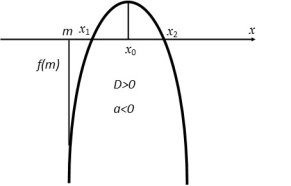
Теорема 1. Корені квадратного тричлена з дійсними коефіцієнтами обидва дійсні і обидва більші даного числа m тоді і тільки тоді, коли

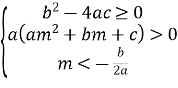            (1)

Згідно умови теореми графік функції    перетинає вісь Ox або дотикається до неї, а точки перетину чи дотику лежать правіше заданої точки m.

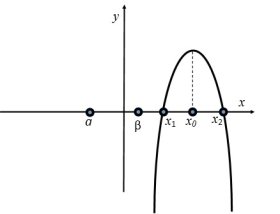
Можливі чотири різних розміщень параболи   y = f(x)   відносно осі Ox і точки m, що задовольняють умову теореми.

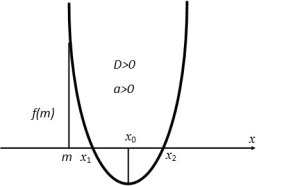Випадок 1.

 

 

 

 

 

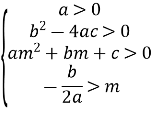
Випадок 2.

 

 

 

 

 

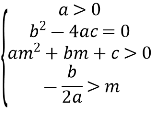
Випадок 3.

 

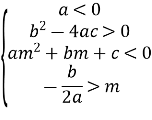
Випадок 4.

 

 

 

 

 

 

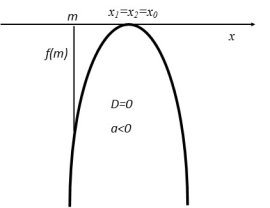
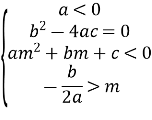
Ці чотири випадки охоплюють всі можливі розміщення параболи, при яких корені квадратного тричлена дійсні і обидва більші за m. Таким чином, об’єднуючи всі частини в одну, одержимо систему (1).

Корені квадратного тричлена належать проміжку тоді, коли

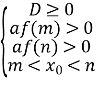
Аналогічно можна дати геометричну інтерпретацію розташування коренів квадратного тричлена для інших випадків:

 

відповідно до цього сформулювати теореми.

Теорема 2. Корені квадратного тричлена з дійсними коефіцієнтами обидва дійсні і обидва менші даного числа n, якщо

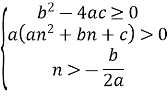
Теорема 3. Корені квадратного тричлена   з дійсними коефіцієнтами обидва дійсні і містяться в інтервалі тоді і тільки тоді

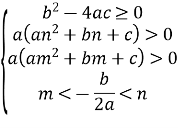
Теорема 4. Для того, щоб корені квадратного тричлена   були дійсні і число знаходилось між ними, необхідно і достатньо, щоб виконувалась умова .

Існують ще випадки, коли:

а) тільки більший корінь квадратного тричлена належить проміжку   ;

б) тільки менший корінь квадратного тричлена належить проміжку   ;

в) проміжок знаходиться в середині проміжку між коренями ;

г) між двома коренями одного тричлена знаходиться тільки один корінь другого тричлена :   де – корені тричлена  

Для всіх випадків сформулювати теореми неможливо, тому потрібно проводити міркування в кожному випадку окремо і користуватися геометричною інтерпретацією.

2. Узагальнення теоретичних міркувань у вигляді опорних таблиць.

Опорний конспект -  1

«Гра» коренів квадратного тричлена

 

 

 

 

 

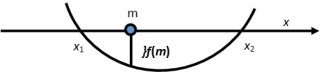
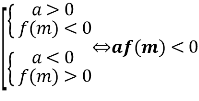
Один з коренів більший за m, другий – менший за m.

 

 

 

 

 

Обидва корені  менші за m.

 

 

 

 

 

 

 

 

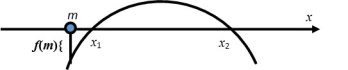
Обидва корені більші за m.

Опорний конспект – 2

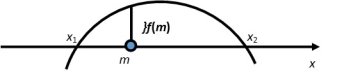
«Гра» коренів квадратного тричлена з інтервалом

 

 

 

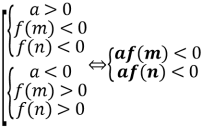
Один з коренів менший за m, другий – більший за n.

 

 

 

 

 

 

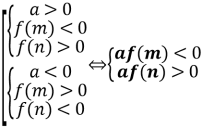
Обидва корені менші за n, але один з коренів більший за m.

 

 

 

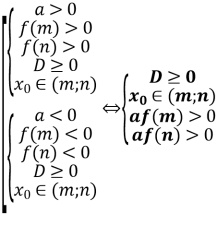
Обидва корені більші за m, але менші за n.

 

3. Приклади розв’язання задач з допомогою міркувань (окремі випадки).

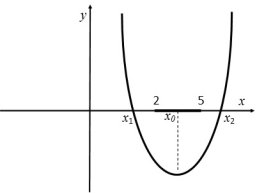
Задача. Знайти всі ті значення параметра m, для яких обидва корені рівняння знаходяться між числами 0 і 2.

Розв’язання. Знайдемо корені рівняння:

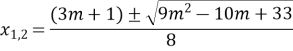
Розв’язати далі дану задачу складно, бо вона зводиться до розв’язання двох подвійних ірраціональних нерівностей. Тому розв’яжемо її графічно.

Тричлен у лівій частині рівняння розглядатимемо як функцію:

 

Схематично побудуємо графік цієї функції:

      для будь яких m

(абсциса вершини параболи)

,       

Відповідно до умов задачі нам підходить тільки таке положення параболи:

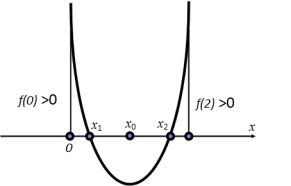
Запишемо це аналітично:

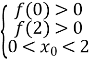  або 

 

 

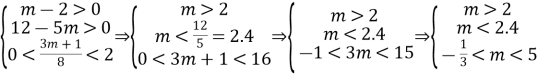
Відповідь .

4. Нерівності з параметрами, пов’язані з дослідженням квадратичної функції.

Не маючи можливості описати всі типи задач з параметрами, зупинимось тільки на найбільш поширених задачах, в яких йде мова про розташування коренів.

Розіб’ємо всі задачі умовно на групи:

1. нерівність виконується для всіх тоді і тільки тоді, якщо

2. нерівність виконується для всіх тоді і тільки тоді, якщо

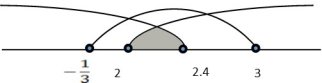
Приклад. При яких значеннях параметра а нерівність

Розв’язання. Згідно 1. маємо:

або

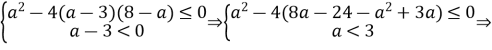
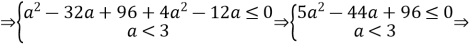
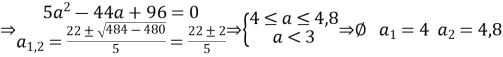
Відповідь. Немає таких значень, при яких буде виконуватись дана нерівність.

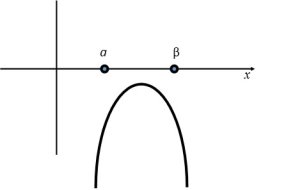3. нерівність виконується для всіх тоді і тільки тоді, якщо:

а)  

 

 

 

 

 

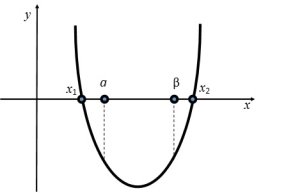
або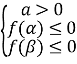  

 

 

 

 

 

 або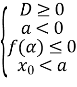 

 

 

 

 

 

 

 

або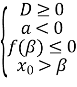   

 

 

 

 

 

б) для виконання нерівності при повинні виконуватись такі умови:

 

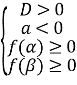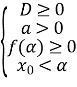або або або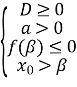

в) нерівність виконується для всіх , якщо:

 

або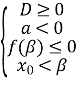

г) а для всіх тоді коли:

або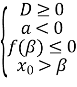

І нарешті нерівність виконується для всіх , тоді і тільки тоді, коли або .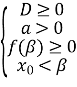

Для всіх , якщо   або .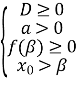

Задача 1. Знайти  всі  значення  параметра  m,  при  яких  нерівність виконується для всіх .

Зобразимо схематично графік функції, що відповідає поставленій умові.

 

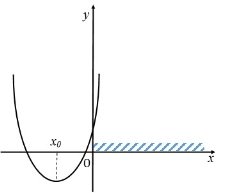
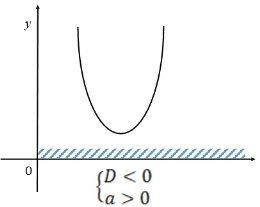
або 

 

 

 

 

 

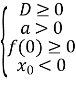
Отже,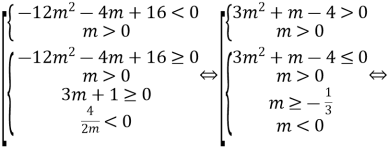

 

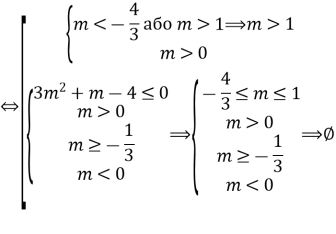
Відповідь:

Задача 2. Знайти всі значення параметра а, при яких нерівність виконується для всіх х таких, що

 

 

 

Отже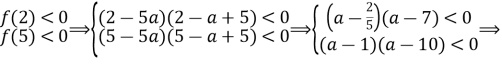

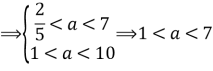
Відповідь:

5. Типові задачі на дослідження квадратичної функції з параметрами.

Розглянемо ще кілька задач на дослідження квадратичної функції (характера коренів, знаків коренів, їх розміщення на числовій осі) залежно від параметра, що входить у коефіцієнти цієї функції.

Задача 1. Для яких значень параметра а квадратний тричлен має тільки цілі корені?

Розв’язання. Покладемо За теоремою Вієта:

де – корені квадратного тричлена. За умовою , а тому і теж цілі числа. З цього слідує, що – ціле число.

Нехай звідки тоді

Якщо – ціле число, то може набувати таких значень: .

Відповідно до цього може набувати таких значень:

Якщо за умовою – цілі числа, то і

Відповідь: ; .

 

Задача 2. Розв’язати і дослідити нерівність

Розв’язання. Знайдемо корені тричлена, що стоїть у лівій частині.

  .

Зазначимо, що

Дослідження.

а)

Якщо і то

Якщо і тобто то бо і .

б) .

Якщо і – суперечність .

Якщо і ; – розв’язків немає.

в) .

Якщо і – суперечність

Якщо і ; – розв’язків немає.

Якщо

Відповідь.

якщо

   якщо

   якщо якщо – розв’язків немає.

6. Модуль і параметр у задачах на дослідження квадратичної функції.

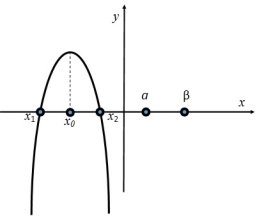
Задача. При яких значеннях параметра а корені рівняння: задовольняють умові ?

Розв’язання.

Умова на корені рівносильна системі  тобто вимозі розташування обох коренів в інтервалі .

Графічне тлумачення вимоги розташування коренів має вигляд

 

 

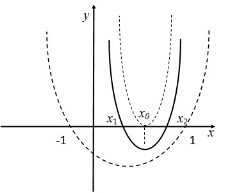
тоді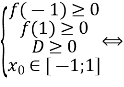

 

 

 

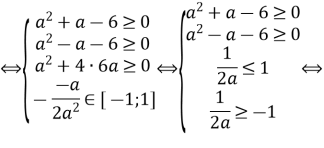
Відповідь: .

Задача 2. При яких дійсних значеннях параметра а нерівність

справджується при всіх

Розв’язання.

Позначимо , тоді

Розглянемо функцію

Графічне тлумачення системи має вигляд:

1).

–  немає коренів.

 

 

 

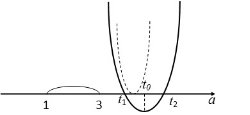У цьому випадку

2).   

 Обидва корені більші за 3 (корені можуть співпадати).

 

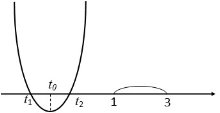У цьому випадку: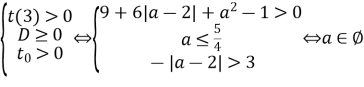

3).    Обидва корені менші за 1 (корені можуть співпадати).

 

У цьому випадку: .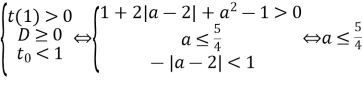

Відповідь:

7. Приклади задач, що приводять до дослідження квадратичної функції.

Задача 1. Довести, що вершина параболи описує пряму лінію.

Доведення. Обчислимо координати вершин параболи:

тобто, маємо систему

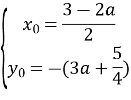
Знайдемо як функцію . Для цього виразимо а з першого рівняння системи і підставимо його в друге рівняння.

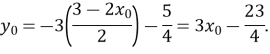
Отже, ордината вершини параболи лінійно залежить від абсциси, причому

Таким чином, довели, що вершина параболи при зміні параметра а описує пряму

Задача 2. При  яких  значеннях  параметра  а  один  з  коренів  рівняння дорівнює подвоєному кореню рівняння .

Розв’язання. Нехай – корені другого рівняння, тоді коренями першого рівняння будуть . Згідно теореми Вієта, запишемо:

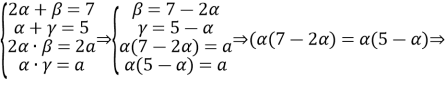
звідси

Відповідь: при

Задача 3. При яких значеннях параметра рівняння

і рівняння мають спільний корінь?

Розв’язання. Нехай – спільний корінь даних рівнянь. Тоді:

+

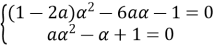
Очевидно тому і

1) при – рівняння спільних коренів не мають (переконуємось перевіркою).

2) при , знаходимо  Підставляючи це значення в рівняння і зробивши перетворення, одержимо рівняння:

Розв’язавши його, знаходимо

Відповідь: при

Висновки

 

Труднощі розв`язування задач з параметрами полягають у тому, що навіть найпростіші рівняння або нерівності потребують виконання розгалуженості всіх значень параметрів на групи, в кожній з яких задача має розв`язок. Саме тому вони вважаються одними з найскладніших в учнівському колі. Крім того, окремої теми на вивчення таких задач шкільною програмою не передбачено.

В роботі розглянуті методи розв`язування задач з параметрами, пов`язані з дослідженням квадратичної функції, показано їх дію на прикладах. Вона допоможе учням запам`ятати наступне:

•         Параметр – це фіксоване, але невідоме число;
•         Розв`язати рівняння, нерівність, систему з параметрами означає для кожного допустимого значення параметра знайти множину всіх коренів даного рівняння, множину всіх розв`язків даної нерівності чи системи;
•         Основний принцип розв`язування задачі з параметром полягає у необхідності розгляду різних випадків у залежності від певних значень параметра;
•         Відповідь до задачі з параметром формується у вигляді запису проміжків зміни параметра з поданням для кожного проміжку розв`язків задачі;
•         Складність задач з параметрами обумовлюється тим, що, як правило, разом зі зміною параметра змінюються не лише коефіцієнти, але й ряд інших характеристик. Зокрема може змінюватися степінь рівняння або нерівності, область допустимих значень тощо.

Скориставшись цією методичною розробкою можна значно допомогти учням опанувати обрану тему і цим самим полегшити їм підготовку до ЗНО, олімпіад, конкурсів, де все частіше зустрічаються задачі вказаного типу.

Використана література

 

1. Апостолова Г. В. Хитромудрий модуль. -  Київ: «Факт»,  2004.

2. Коваленко В. Г., Кривошеєв В. Я., Старосельцев О. В. Алгебра: експериментальний навчальний посібник для 9 класу. – К.: «Освіта», 1996.

3. Кравчук В. Р., Козира. В. М, Гап`юк Є. Ф., Гринчишин Я. Т. Алгебра: пробний підручник для 10 класу шкіл, ліцеїв та гімназій фізико-математичного профілю. – Тернопіль. «Підручники та посібники», 1997.

4. Нелін Є. П. Алгебра і початки аналізу: дворівневий підручник для 10 класу загальноосвітніх навчальних закладів. – К.: «Світ дитинства», 2004.

5. Шарова Л. І. Рівняння і нерівності: посібник для підготовчих відділень. – К.: «Вища школа», 1981.

6. Шкіль М. І., Колесник Т. В., Хмара Т. М. Алгебра і початки аналізу: підручник для 9-11 класів з поглибленим вивченням математики в середніх закладах освіти. – К.: «Освіта», 2001.