Методика розв'зування діофантових рівняннь різних типів.
Вступ
Розділ І. Загальні теоретичні відомості
- Лінійні діофантові рівняння.
- Невизначені рівняння вищих порядків.
2.1 Рівняння![]() . Піфагорові трійки.
. Піфагорові трійки.
2.2 Рівняння Ферма.
2.3 Невизначене рівняння третього порядку.
2.4 Рівняння Лежандра.
Висновок до Розділу І
Розділ ІІ. Методи та приклади розв’язання діофантових рівнянь
- Алгоритм знаходження розв’язків діофантового рівняння.
- Основні методи розв’язування діофантових рівнянь в класах поглибленого вивчення математики.
- Метод біноміальних перетворень при розв’язуванні показникаових діофантових рівнянь.
-
Застосування алгоритму Евкліда для розв’язання невизначеного рівняння
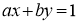 .
.
-
Спосіб розв’язання – використання розв’язків рівняння
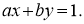
-
Спосіб розв’язання – використання розв’язків рівняння
- Розв’язування лінійних діофантових рівнянь.
- Розв’язування діофантових рівнянь вищих порядків.
- Задачі математичних олімпіад.
Висновок до Розділу І І
Загальні висновки
Вступ
Діофант представляє одну із найцікавіших особистостей в історії математики. Ми не знаємо, ким був Діофант, точні роки його життя, не відомі його попередники, які працювали у тій же сфері, що й він.
Дуже цікавою є діяльність Діофанта. До нас дійшло 7 книг із 13, які були об’єднані в «Арифметику». Стиль і зміст цих книг дуже відрізняється від класичних книг з теорії чисел та алгебри, зразки яких ми знаємо з «Начал» Евкліда, лем Архімеда і Аполлонія. «Арифметика», безсумнівно, є результатом багаточисленних досліджень, велика кількість з яких залишилась нам невідомою.
У книгах Діофанта, що збереглися, міститься 189 задач із розв’язаннями. У першій книзі викладено задачі, які приводяться до визначених рівнянь першого та другого степеня. Решта п’ять книг містять невизначені рівняння. У цих книгах ще немає систематичної теорії невизначених рівнянь, методи розв’язування змінюються час від часу. Діофант задовольняється певним розв’язком, цілим чи дробовим, аби він був додатним.
Проте методи розв’язування невизначених рівнянь складають основний внесок Діофанта в математику. Так що ж таке діофантове рівняння?
Діофантові рівняння — це алгебраїчні рівняння або системитаких рівнянь з двома або більшою кількістю змінних із цілими коефіцієнтами, для яких знаходяться цілі чи раціональні розв’язки; при цьому кількість змінних у діофантовому рівнянні більша від кількості рівнянь.
Розділ математики, що вивчає діофантові рівняння, називається діофантовим аналізом, який, у свою чергу, є частиною розділу сучасної математики — теорії чисел. У теорії чисел створені спеціальні методи розв’язування діофантових (їх ще називають невизначеними) рівнянь.
«Арифметика» Діофанта – це збірник задач (їх всього 189), кожна з яких має розв'язок і необхідні пояснення. В збірник входять різноманітні задачі, і їх розв’язки дуже часто не так просто зрозуміти. Діофант практикувався у знаходження розв’язків невизначених рівнянь вигляду:
![]() ,
, ![]() ,
,
систем таких рівнянь. Його цікавили тільки додатні цілі числа і раціональні розв’язки. Ірраціональні розв’язки він називав «неможливими» і ретельно підбирав коефіцієнти так, щоб отримати шукані додатні, раціональні розв’язки.
Тому, зазвичай, довільне невизначене рівняння (але, як правило, з цілими коефіцієнтами) називають «діофантовим», якщо хочуть наголосити на тому, що рівняння слід розв’язувати в цілих числах.
Невизначені рівняння першого степеня почали розглядати математики, приблизно в ![]() столітті. Деякі такі рівняння з двома, трьома невідомими з’явились у зв’язку з проблемами, які виникли в астрономії, наприклад, при розгляді питань, пов’язаних з визначенням періодичного повторення небесних явищ.
столітті. Деякі такі рівняння з двома, трьома невідомими з’явились у зв’язку з проблемами, які виникли в астрономії, наприклад, при розгляді питань, пов’язаних з визначенням періодичного повторення небесних явищ.
В 1624 році була опублікована книга французького математика Баше де Мезирьяка , у якій для розв'язку рівняння ![]() фактично застосовується процес, що зводиться до послідовного визначення неповних часткових підхідних дробів.
фактично застосовується процес, що зводиться до послідовного визначення неповних часткових підхідних дробів.
Після Баше в ![]() і
і ![]() століттях різні алгоритми для розв'язку невизначеного рівняння першого степеня з двома невідомими давали Роль, Ейлер та інші математики.
століттях різні алгоритми для розв'язку невизначеного рівняння першого степеня з двома невідомими давали Роль, Ейлер та інші математики.
Ланцюгові дроби для розв'язку таких рівнянь були застосовані вперше Лагранжем. Пізніше діофантові рівняння стали записувати і розв’язувати у формі конгруенцій.
У серпні 1900 року в Парижі відбувся ![]() міжнародний конгрес математиків. 8 серпня Д. Гільберт прочитав на цьому конгресі доповідь «Математичні проблеми». Серед 23 проблем, розв'язок яких, як вважав Гільберт, було необхідно отримати в наступному
міжнародний конгрес математиків. 8 серпня Д. Гільберт прочитав на цьому конгресі доповідь «Математичні проблеми». Серед 23 проблем, розв'язок яких, як вважав Гільберт, було необхідно отримати в наступному ![]() столітті , десяту проблему він сформулював наступним чином:
столітті , десяту проблему він сформулював наступним чином:
«Нехай задано діофантове рівняння з довільним числом невідомих і раціональними числовими коефіцієнтами. Вказати спосіб, за допомогою якого можна після скінченного числа операцій встановити, чи розв’язне це рівняння в цілих числах ».
Гіпотезу, що такого способу не існує, першим сформулював (з вагомими на те доказами) американський математик М. Девіс у 1949 році. Доведення цієї гіпотези затягнулося на 20 років – останній крок був зроблений в 1970 році Юрієм Володимировичем Мятиясеєвичем , на першому році аспірантури він показав алгоритмічну нерозв’язність 10 –ї проблеми Гільберта.
Проте, якщо про довільне діофантове рівняння не можна сказати чи має воно цілі корені, чи не має, то проблема існування цілих коренів лінійного діофантового рівняння розв’язана.
Традиційно основним завданням шкільного курсу алгебри є навчити учнів розв'язувати рівняння та задачі, що зводяться до них. Недаремно упродовж багатьох років алгебру розглядали як науку про рівняння і способи їх розв'язування. Велике значення рівнянь підкреслював А.Ейнштейн, він казав: «Мені доводиться ділити свій час між політикою і рівняннями. Проте рівняння, на мій погляд, набагато важливіші, тому що політика існує тільки для даного часу, а рівняння будуть існувати вічно». Не можна стверджувати що, наприклад, тема «Функції» має меншу важливість, але навіть функцію, з певної точки зору, можна розглядати, як рівняння виду ![]() , що виконується за певних умов та має певні властивості. Крім цього, слід відзначити, що багато задач шкільного курсу геометрії теж розв'язується алгебраїчним способом, тобто за допомогою рівнянь. Отже, без уміння розв'язувати рівняння різного типу та різного ступеня складності не можна оволодіти шкільною програмою з математики.
, що виконується за певних умов та має певні властивості. Крім цього, слід відзначити, що багато задач шкільного курсу геометрії теж розв'язується алгебраїчним способом, тобто за допомогою рівнянь. Отже, без уміння розв'язувати рівняння різного типу та різного ступеня складності не можна оволодіти шкільною програмою з математики.
Вперше з рівняннями учні зустрічаються на уроках математики в початковій школі, як тільки починають вивчати дії з натуральними числами. Але способи розв’язування рівнянь у 1 – 4 класах ґрунтуються на правилах визначення невідомого компоненту тої чи іншої дії: невідомого доданка, зменшуваного, від'ємника, множника тощо. І лише в 6 – 7 класах починають розглядати більш науковий, більш строгий підхід до рівнянь: дають означення рівняння як рівності, що має змінну, вводять поняття кореня рівняння, дають відповідь на запитання «Що означає розв'язати рівняння?», а головне, вводять основні властивості рівнянь, на яких і базуються усі їх способи розв'язування, незалежно від типу і складності. Крім цього, під час вивчення теми «Рівняння та їх властивості» (6—7 клас) учні починають розв'язувати рівняння, в яких змінна знаходиться у двох частинах одночасно. Отже, в 6 – 7 класах узагальнюються всі знання і навички учнів щодо розв'язування рівнянь першого степеня, зведення їх до лінійних або до рівнянь вигляду![]() .
.
Поступово вигляд і способи розв'язування рівнянь ускладнюються. Упродовж вивчення алгебри учні опановують уміння розв'язувати квадратні, ірраціональні, логарифмічні, тригонометричні, показникові рівняння, а також їх системи, але, на жаль, усі ці рівняння відносяться до так званих визначених, тобто рівнянь з однією змінною або (якщо це система) систем, де кількість змінних дорівнює кількості рівнянь. Загальноприйнята шкільна програма з математики зовсім «забула» про існування невизначених рівнянь (рівнянь, що мають кілька змінних або систем, де кількість змінних більша від кількості рівнянь). Задачі на подібні рівняння зустрічаються лише на математичних олімпіадах. Виникає питання: якщо учень не знайомий навіть з основами теорії невизначених рівнянь, як же він буде їх розв'язувати? Тому за доцільне буде ознайомити учнів з найпростішими невизначеними, або діофантовими рівняннями під час вивчення відповідних тем шкільної програми з алгебри. До речі, не всі невизначені рівняння є діофантовими. Діофантовими називаються лише ті алгебраїчні рівняння або їх системи з цілими коефіцієнтами, в яких кількість змінних більша, ніж кількість рівнянь, а знайти треба тільки цілі або раціональні розв'язки. Отже, до діофантових рівнянь найчастіше зводяться задачі, за змістом яких невідомі значення величин можуть бути тільки цілими числами. Важливість даної теми ще й у тому, що діофантові рівняння дають велику можливість для розвитку логічного мислення учнів, бо загальних способів їх розв'язування немає, до кожного типу рівнянь треба підходити творчо, використовуючи пошукові методи, які, в першу чергу, направлені на формування учня як особистості, здатної до самостійної, творчої і діяльності.
Коли ж ми можна розпочати знайомство учнів з найпростішими діофантовими рівняннями? Слід підкреслити, що невизначені рівняння все ж таки з'являються в шкільному курсі алгебри. У 7 класі вводять поняття лінійного рівняння з двома змінними або рівняння вигляду![]() , вводять означення розв'язку подібного рівняння, а потім переходять до його геометричного змісту, але алгебраїчні способи розв'язування при цьому не розглядаються. Саме у цій темі можна почати розглядати основи теорії невизначених рівнянь першого степеня. Потім у 8 класі під час вивчення теми „Квадратні рівняння” показати способи розв’язування найпростіших діофантових рівнянь другого степеня і т. д.
, вводять означення розв'язку подібного рівняння, а потім переходять до його геометричного змісту, але алгебраїчні способи розв'язування при цьому не розглядаються. Саме у цій темі можна почати розглядати основи теорії невизначених рівнянь першого степеня. Потім у 8 класі під час вивчення теми „Квадратні рівняння” показати способи розв’язування найпростіших діофантових рівнянь другого степеня і т. д.
За чинною програмою 5 – 11 класів діофантові рівняння вивчаються у факультативному курсі в 9 класі. На вивчення даної теми відводиться 4 години.
Навчальний посібник містить історичний аспект вивчення діофантових рівнянь, методи розв’язання лінійних діофантових рівнянь: метод спуску, метод ланцюгових дробів; для визначення частинних розв’язків – способи підбору, підстановки, алгоритм Евкліда тощо. Подано також приклади розв’язання діофантових рівнянь вищих степенів та конкурсні задачі, моделлю розв’язання яких є діофантові рівняння.
Розділ І. Загальні теоретичні відомості
§1. Лінійні діофантові рівняння
Діофантовим рівнянням першого степеня з


про публікацію авторської розробки
Додати розробку
