Методика викладання комплексних чисел

Проєкт «МЕТОДИКА ВИВЧЕННЯ КОМПЛЕКСНИХ ЧИСЕЛ У КЛАСАХ ІЗ ПОГЛИБЛЕНИМ ВИВЧЕННЯМ МАТЕМАТИКИ».

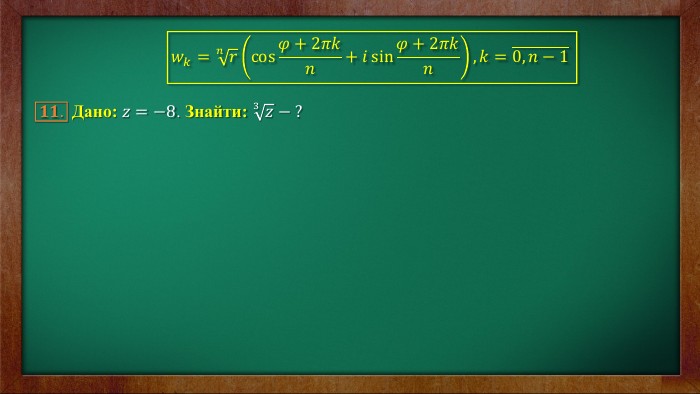
Алгебраїчна форма комплексного числа Означення. Комплексним числом називають вираз виду 𝑎+𝑏𝑖, де 𝑎 та 𝑏 ­– дійсні числа, 𝑖 – уявна одиниця, яка визначається рівністю 𝑖2=−1. Комплексні числа часто позначають однією літерою: 𝑧=𝑎+𝑏𝑖. Число 𝑎 при цьому називають дійсною частиною, а число 𝑏 – уявною частиною комплексного числа 𝑧=𝑎+𝑏𝑖. Символічно їх позначають так: 𝑎=𝑅𝑒 𝑧, 𝑏=𝐼𝑚 𝑧. Зауваження. Будь-яке дійсне число можна розглядати як комплексне число, в якого уявна частина дорівнює 0: 𝑎=𝑎+0⋅𝑖 .  

Означення. Два комплексні числа 𝑧1=𝑎1+𝑏1𝑖 та 𝑧2=𝑎2+𝑏2𝑖 називають рівними тоді і тільки тоді, коли 𝑎1=𝑎2 та 𝑏1=𝑏2, тобто 𝑧1=𝑧2𝑎1+𝑏1𝑖=𝑎2+𝑏2𝑖 ⇔𝑎1=𝑎2𝑏1=𝑏2 Означення. Комплексне число 𝑧=𝑦𝑖, в якому 𝑅𝑒 𝑧=0 називають суто уявним числом. 

Дії над комплексними числами у алгебраїчній форміОзначення. Сумою комплексних чисел 𝑧1=𝑎1+𝑏1𝑖 та 𝑧2=𝑎2+𝑏2𝑖 є комплексне число 𝑧, дійсна частина якого дорівнює сумі дійсних частин, а уявна частина – сумі уявних частин, тобто𝒛𝟏+𝒛𝟐=𝒂𝟏+𝒂𝟐+𝒃𝟏+𝒃𝟐𝒊Зауваження. Про число 𝑧 кажуть, що його дістали внаслідок додавання комплексних чисел 𝑧1 і 𝑧2, і записують 𝑧=𝑧1+𝑧2. Числа 𝑧1 і 𝑧2 звуть доданками. Властивості операції додавання комплексних чисел:1) асоціативність: 𝑧1+𝑧2+𝑧3=𝑧1+𝑧2+𝑧3;2) комутативність: 𝑧1+𝑧2=𝑧2+𝑧1. 

Означення. Комплексне число −𝑎−𝑏𝑖 називається протилежним комплексному числу 𝑎+𝑏𝑖. Комплексне число, протилежне комплексному числу 𝑧, позначається −𝑧. Зауваження. Сума комплексних чисел 𝑧 і −𝑧 дорівнює нулю 𝑧+(−𝑧)=0. .𝟏. Дано: 𝑧1=2+5𝑖, 𝑧2=1−7𝑖. Знайти: 𝑧1+𝑧2.𝟐. Дано: 𝑧1=2𝑖, 𝑧2=8−𝑖. Знайти: 𝑧1+𝑧2. 

Означення. Різниця комплексних чисел 𝑧1=𝑎1+𝑏1𝑖 та 𝑧2=𝑎2+𝑏2𝑖 є комплексне число 𝑧, що є сумою числа 𝑧1 і числа протилежного 𝑧2𝒛=𝒛𝟏+(−𝒛𝟐)=𝒂𝟏−𝒂𝟐+𝒃𝟏−𝒃𝟐𝒊,тобто комплексним числом, дійсна і уявна частини якого дорівнюють відповідно різниці дійсних і уявних частин зменшуваного і від'ємника. Зауваження. Про число 𝑧 кажуть, що його дістали внаслідок віднімання комплексного числа 𝑧2 від комплексного числа 𝑧1, і записують 𝑧=𝑧1−𝑧2.𝟑. Дано: 𝑧1=3−9𝑖, 𝑧2=7+𝑖. Знайти: 𝑧1−𝑧2. 

Означення. Добутком комплексних чисел 𝑧1=𝑎1+𝑏1𝑖 та 𝑧2=𝑎2+𝑏2𝑖 є комплексне число: 𝒛=𝒛𝟏⋅𝒛𝟐=𝒂𝟏𝒂𝟐−𝒃𝟏𝒃𝟐+𝒂𝟏𝒃𝟐+𝒂𝟐𝒃𝟏𝒊Зауваження. Про число 𝑧 кажуть, що його дістали внаслідок множення комплексного числа 𝑧1 на комплексне число 𝑧2, і записують 𝑧=𝑧1𝑧2. Числа 𝑧1 і 𝑧2 називають співмножниками. Властивості операції множення комплексних чисел:1) асоціативність: 𝑧1𝑧2𝑧3=𝑧1𝑧2𝑧3;2) комутативність: 𝑧1𝑧2=𝑧2𝑧1.3) додавання і множення комплексних чисел зв'язані правилом, яке називається законом дистрибутивності множення відносно додавання: 𝑧1+𝑧2𝑧3=𝑧1𝑧3+𝑧2𝑧3. 

𝟒. Дано: 𝑧1=1+2𝑖, 𝑧2=3−𝑖. Знайти: 𝑧1⋅𝑧2 (двома способами). 

Означення. Часткою двох комплексних чисел 𝑧1 та 𝑧2 𝑧2≠0 є таке комплексне число 𝑧, що 𝑧1=𝑧𝑧2 . Частку комплексних чисел 𝑧1=𝑎1+𝑏1𝑖 та 𝑧2=𝑎2+𝑏2𝑖 обчислюють за формулою:𝒛=𝒛𝟏𝒛𝟐=𝒂𝟏𝒂𝟐+𝒃𝟏𝒃𝟐𝒂𝟐𝟐+𝒃𝟐𝟐+𝒂𝟐𝒃𝟏−𝒂𝟏𝒃𝟐𝒂𝟐𝟐+𝒃𝟐𝟐𝒊Зауваження. Про число 𝑧 кажуть, що його дістали внаслідок ділення комплексного числа 𝑧1 на комплексне число 𝑧2, і записують 𝑧=𝑧1𝑧2. Зауваження. Ця формула дозволяє відразу обчислити частку двох комплексних чисел, але користуватись нею досить незручно. При розв’язанні прикладів, як правило, домножують чисельник та знаменник дробу на число, спряжене до знаменника. 

Означення. Комплексне число 𝑎 –𝑏𝑖 називається спряженим до комплексного числа 𝑧 = 𝑎 +𝑏𝑖 та позначають 𝑧=𝑎 –𝑏𝑖. Зауваження. Сума та добуток спряжених комплексних чисел завжди є дійсним числом. Дійсно, для будь-якого числа 𝑧 = 𝑎 + 𝑏𝑖:𝑧+𝑧=𝑎 +𝑏𝑖+𝑎−𝑏𝑖=𝑎+𝑎+𝑏−𝑏𝑖=2𝑎𝑧⋅𝑧=𝑎 +𝑏𝑖⋅𝑎−𝑏𝑖=𝑎2+𝑎𝑏𝑖−𝑎𝑏𝑖−𝑏𝑖2=𝑎2+𝑏2 

𝟓. Дано: 𝑧1=23+𝑖, 𝑧2=3+𝑖. Знайти: 𝑧1𝑧2 (двома способами). 

𝟔. Обчислити: 1𝑖−2. 

Піднесення уявної одиниці до ступеня𝒊𝟏=𝒊 𝒊𝟐=−𝟏 𝒊𝟑=𝒊𝟐⋅𝒊=−𝒊 𝒊𝟒=𝒊𝟑⋅𝒊=𝟏𝒊𝟓=𝒊𝟒⋅𝒊=𝒊 𝒊𝟔=𝒊𝟓⋅𝒊=−𝟏 𝒊𝟕=𝒊𝟔⋅𝒊=−𝒊 𝒊𝟖=𝒊𝟕⋅𝒊=𝟏 Ми бачимо, що величина 𝑖𝑛, де 𝑛 – деяке натуральне число, може прийматилише чотири значення: 𝑖 , −1, −𝑖 та 1. Для того, щоб обчислити величину 𝑖𝑛,треба представити число 𝑛 у вигляді 𝑛=4𝑘, 𝑛=4𝑘+1, 𝑛=4𝑘+2 або𝑛=4𝑘+3, де k – натуральне число (інакше кажучи, треба поділити 𝑛 на 4 з остачею)  𝒊4𝒌=𝒊4𝒌=1𝒌=1  𝒊4𝒌+1=𝒊4𝒌⋅𝒊=1⋅𝒊=𝒊𝒊4𝒌+2=𝒊4𝒌⋅𝒊2=1⋅𝒊2=1⋅−1=−1𝒊4𝒌+3=𝒊4𝒌⋅𝒊3=1⋅𝒊3=1⋅−𝒊=−𝒊 

𝟕. Обчисліть:а) 𝑖191 б) 𝑖100 в) 𝑖365 г) 𝑖2023 

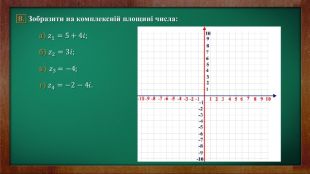
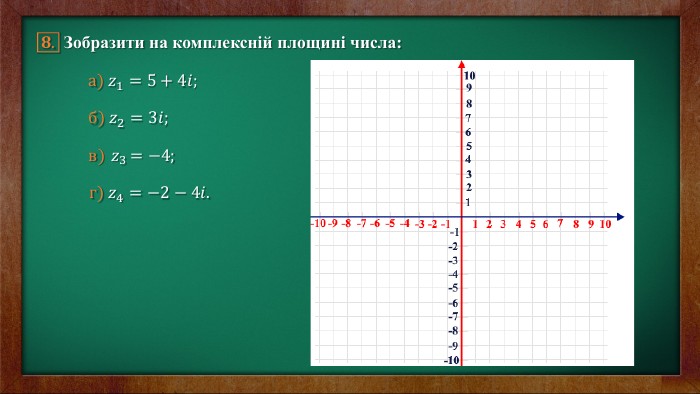
Геометричне зображення комплексного числа Подібно до того, як дійсні числа можна зображати точками числової прямої, комплексні числа можна зображати точками площини. Можливість такого зображення ґрунтується на ототожненні множини комплексних чисел 𝑎+𝑏𝑖 множини пар дійсних чисел (𝑎;𝑏), які в прямокутній системі координат О𝑥у можна трактувати як координати точок площини.  Далі, з кожною точкою 𝐴 координатної площини 𝑂𝑥𝑦 можна зв'язати вектор 𝑂𝐴, який виходить з початку координат і закінчується y точці 𝐴. Тому комплексні числа допускають ще одну геометричну інтерпретацію: кожне комплексне число 𝑎+𝑏𝑖 можна геометричне інтерпретувати як вектор 𝑂𝐴 з координатами (𝑎;𝑏). Координати вектора 𝑂𝐴 при цьому будуть такими ж, як і координати точки 𝐴, а саме (𝑎;𝑏). 𝑦 𝑂 𝐴 𝑏 𝑎 𝑥 

Тригонометрична форма комплексного числа Виберемо на площині прямокутнику декартову систему координат. Якщо кожному комплексному числу 𝑧=𝑎+𝑏𝑖 поставити у відповідність точку 𝑎;𝑏 площини 𝑥𝑂𝑦, то між множиною всіх комплексних чисел і множиною всіх точок площини буде встановлено взаємно однозначну відповідність. Дійсні числа при цьому зображуються точками осі Ох , а суто уявні числа – точками осі Оу . Тому вісь Ох називають дійсною, а вісь Оу – уявною. Числу 𝑧=0 відповідає точка 𝑂0;0. 

𝟖. Зобразити на комплексній площині числа:а) 𝑧1=5+4𝑖; б) 𝑧2=3𝑖; в) 𝑧3=−4; г) 𝑧4=−2−4𝑖. 

Як відомо, комплексне число 𝑧=𝑎+𝑏𝑖 можна також зображати вектором, початок якого знаходиться у точці 0;0, а кінець – в точці 𝑎;𝑏. Такий вектор називають радіус-вектором точки 𝑎;𝑏. Довжину радіус-вектора називають модулем комплексного числа і позначають 𝑧 , 𝜌 або 𝑟 . Кут 𝜑, який утворює радіус-вектор точки 𝑧 з додатним напрямком осі 𝑂𝑥, називають аргументом комплексного числа і позначають 𝐴𝑟𝑔 𝑧 : 𝜑=𝐴𝑟𝑔 𝑧. 𝒓=𝒂𝟐+𝒃𝟐 𝒄𝒐𝒔 𝝋=𝒂𝒓𝒔𝒊𝒏 𝝋=𝒃𝒓 

При цьому: 𝑎=𝑟cos𝜑, 𝑏=𝑟𝑠𝑖𝑛𝜑, тому 𝑧=𝑎+𝑏𝑖=𝑟cos𝜑+𝑟sin𝜑⋅𝑖. Отже,𝒛=𝑟cos𝜑+𝑖𝑠𝑖𝑛𝜑 – тригонометрична форма комплексного числа. Зауваження. Кожне комплексне число має модуль, причому 0≤𝑟<+∞, 𝑟=0, тоді й тільки тоді, коли 𝑧=0. Аргумент числа 𝑧=0 невизначений, а для всіх інших комплексних чисел аргумент визначається не однозначно, а з точністю до сталого доданку виду 2𝜋𝑘, де 𝑘∈ℤ. Наприклад, якщо 𝑧=1+𝑖, то аргументом 𝑧 може бути будь-яке із чисел 𝜋4, 𝜋4±2𝜋, 𝜋4±4𝜋, …, тобто 𝐴𝑟𝑔 1+𝑖=𝜋4+2𝜋𝑘, 𝑘∈ℤ. Означення. Головним значенням аргументу вважають те значення кута 𝜑, яке задовольняє нерівності −𝜋<𝜑≤𝜋 . Це значення позначають через 𝑎𝑟𝑔 𝑧.𝑨𝒓𝒈 𝒛=𝒂𝒓𝒈 𝒛+𝟐𝝅𝒌, 𝒌∈ℤ 

𝟗. Запишіть число у тригонометричній формі: а) 𝑧1=5; б) 𝑧2=𝑖; в) 𝑧3=−2; г) 𝑧4=−𝑖;д) 𝑧5=1+𝑖;е) 𝑧6=−3+𝑖. 

Комплексні числа. Задачі для практичного заняття𝟏. Дано: 𝑧1=4+5𝑖, 𝑧2=3−2𝑖. Знайти: а) 𝑧1+𝑧2; б) 𝑧2−𝑧1; в) 𝑧1⋅𝑧2; г) 𝑧1𝑧2. 

Комплексні числа. Задачі для практичного заняття𝟐. Обчислити: 5+𝑖7−6𝑖3+𝑖.𝟑. Запишіть число у тригонометричній формі: а) 1−𝑖; б) −2+2𝑖. 

Комплексні числа. Задачі для практичного заняття𝟒. Обчисліть:а) 𝑖47; б) 𝑖122; в) 𝑖2040; г) 𝑖93. 

Дії над комплексними числами у тригонометричній форміТеорема 1. Нехай комплексні числа 𝑧1 та 𝑧2 записані в тригонометричній формі:𝑧1=𝑟1cos𝜑1+𝑖sin𝜑1𝑧2=𝑟2cos𝜑2+𝑖sin𝜑2 Тоді 𝒛𝟏⋅𝒛𝟐=𝒓𝟏⋅𝒓𝟐𝐜𝐨𝐬𝝋𝟏+𝝋𝟐+𝒊𝐬𝐢𝐧𝝋𝟏+𝝋𝟐𝒛𝟏𝒛𝟐=𝒓𝟏𝒓𝟐𝐜𝐨𝐬𝝋𝟏−𝝋𝟐+𝒊𝐬𝐢𝐧𝝋𝟏−𝝋𝟐 

𝟔. Дано: Знайти:𝑧1=3cos𝜋7+𝑖sin𝜋7 𝑧2=4cos6𝜋7+𝑖sin6𝜋7   а) 𝑧1⋅𝑧2; б) 𝑧17; Знайти: Комплексні числа. Задачі для практичного заняття

𝟔. Дано: Знайти:𝑧1=3cos𝜋7+𝑖sin𝜋7 𝑧2=4cos6𝜋7+𝑖sin6𝜋7   в) 𝑧2−3; г) 𝑧2𝑧1. Знайти: Комплексні числа. Задачі для практичного заняття

Теорема 2. Нехай 𝑧𝑘=𝑟𝑘cos𝜑𝑘+𝑖sin𝜑𝑘, 𝑘=1,2,…,𝑛, тоді𝒛𝟏⋅𝒛𝟐⋅…⋅𝒛𝒌==𝒓𝟏⋅𝒓𝟐⋅…⋅𝒓𝒌𝐜𝐨𝐬𝝋𝟏+𝝋𝟐+ … +𝝋𝒌+𝒊𝐬𝐢𝐧𝝋𝟏+𝝋𝟐+ … +𝝋𝒌Наслідок. У випадку, коли 𝑧1=𝑧2= … =𝑧𝑛=𝑧=𝑟cos𝜑+𝑖sin𝜑, формула приймає наступний вигляд:𝒛𝒏=𝒓𝐜𝐨𝐬𝝋+𝒊𝐬𝐢𝐧𝝋𝒏=𝒓𝒏𝐜𝐨𝐬𝒏𝝋+𝒊𝐬𝐢𝐧𝒏𝝋, де 𝑛∈ℤ 

Формула Муавра𝒛𝒏=𝒓𝒏𝐜𝐨𝐬𝒏𝝋+𝒊𝐬𝐢𝐧𝒏𝝋 𝟏𝟎. Обчисліть:а) 𝑧=−1+𝑖39  

Формула Муавра𝒛𝒏=𝒓𝒏𝐜𝐨𝐬𝒏𝝋+𝒊𝐬𝐢𝐧𝒏𝝋 𝟏𝟎. Обчисліть: б) 1+𝑖2023 

Комплексні числа. Задачі для практичного заняття𝟓. Знайти дійсну та уявну частину комплексного числа: а) 𝑧=1+𝑖1−𝑖11 

Комплексні числа. Задачі для практичного заняття𝟓. Знайти дійсну та уявну частину комплексного числа: б) 𝑧=2+2𝑖5 

Добування кореня 𝑛–го ступеня із комплексного числа Означення. Коренем 𝑛-го ступеня із комплексного числа 𝑧 називають комплексне число 𝑤, яке при піднесенні до ступеня 𝑛 дає 𝑧, тобто:𝑤=𝑛𝑧⟺𝑤𝑛=𝑧Якщо 𝑧=0, то 𝑛𝑧=0 для будь-якого 𝑛. Нехай 𝑧≠0. Теорема. Існує рівно 𝑛 значень кореня 𝑛-го ступеня із комплексного числа 𝑧=𝑟cos𝜑+𝑖sin𝜑, 𝑧≠0. Ці значення визначаються формулою:𝑤𝑘=𝑛𝑧=𝑛𝑟cos𝜑+𝑖sin𝜑=𝑛𝑟cos𝜑+2𝜋𝑘𝑛+𝑖sin𝜑+2𝜋𝑘𝑛, де𝑘=0,1,2,…,𝑛−1=0,𝑛−1 

𝟏𝟏. Дано: 𝑧=−8. Знайти: 3𝑧 − ? 𝑤𝑘=𝑛𝑟cos𝜑+2𝜋𝑘𝑛+𝑖sin𝜑+2𝜋𝑘𝑛,𝑘=0,𝑛−1  

Комплексні числа. Задачі для практичного заняття𝟕. Дано: 𝑧=2cos3𝜋4+𝑖sin3𝜋4 . Знайти: 3𝑧 − ? 

Добування кореня 𝑛–го ступеня із одиниці𝟏=𝐜𝐨𝐬𝟎°+𝒊𝐬𝐢𝐧𝟎° Отже, 𝜺𝒌=𝐜𝐨𝐬𝟐𝝅𝒌𝒏+𝒊𝐬𝐢𝐧𝟐𝝅𝒌𝒏 , де𝑘=0,1,2,…,𝑛−1=0,𝑛−1 Означення. 𝜀𝑘 будемо називати примітивним (первісним) коренем 𝑛-го ступеня з одиниці, якщо 𝑛 – це найменше натуральне число, таке що 𝜀𝑘𝑛=1. Критерій примітивності. 𝜀𝑘 буде примітивним коренем 𝑛-го ступеня з одиниці, тоді і тільки тоді, коли 𝑛 і 𝑘 взаємно прості числа, тобто: 

𝟏𝟐. Знайти всі корені з одиниці 4 ступеню.  

Зауваження. На комплексній площині кореням 𝑛-го ступеня з одиниці відповідають вершини правильного 𝑛-кутника, вписаного в одиничне коло з центром у початку координат, причому одна з вершин відповідає числу 1. 

Комплексні числа. Задачі для практичного заняття𝟖. Знайти всі примітивні корені з одиниці 12 ступеню.  

Комплексні числа. Задачі для практичного заняття𝟗. Знайти всі корені рівняння:a) 𝑧2+6𝑧+34=0; 

Комплексні числа. Задачі для практичного заняття𝟗. Знайти всі корені рівняння:б) 𝑧2+36=0; 

Комплексні числа. Задачі для практичного заняття𝟗. Знайти всі корені рівняння:в) 𝑧4−5𝑧2−36=0; 

Комплексні числа. Задачі для практичного заняття𝟗. Знайти всі корені рівняння:г) 𝑧3+𝑧−2=0. 

Дякую за увагу!