Презентація "Комбінаторика. Найпростіші комбінаторні задачі"
Про матеріал
Презентація містить необхідний теоретичний мінімум та тренувальні вправи у вигляді тестових завдань. Підійде і для роботи на уроці, і для дистанційного навчання учнів.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



































-

Kлачик Альона Ярославівна
23.05.2024 в 19:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
12.03.2023 в 11:12
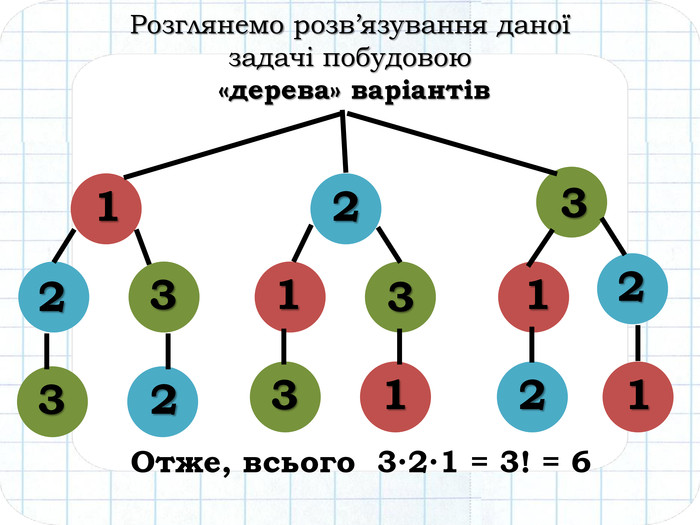
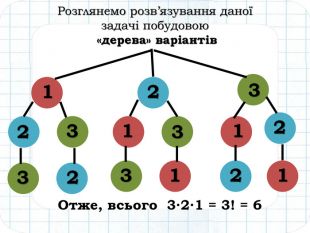
Шикарно подано. Важливо показати "спосіб дерева".
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

ночовка валентина
07.12.2022 в 08:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Скрипнюк Марія
31.05.2022 в 11:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тимченко Олена Василівна
13.04.2022 в 19:13
Дякую, що даєте можливість користуватися. Дай Боже здоров'я.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сипченко Тетяна Миколаївна
11.04.2021 в 20:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

суріна надія Олександрівна
06.02.2021 в 09:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рязанова Галина Яківна
08.12.2020 в 01:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Букарева Анастасія Анатоліївна
17.11.2019 в 21:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
07.05.2019 в 19:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Anikeienko Alla
20.11.2018 в 20:39
Чудово
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прошак Сергій Володимирович
28.10.2018 в 19:58
Щиро дякую! Удачі Вам.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самборська Олена Дмитрівна
09.10.2018 в 12:52
Чудово!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 10 відгуків