Презентація "Основи математичної статистики"
Про матеріал
Презентація містить необхідний теоретичний мінімум, зразки розв'язання статистичних задач і завдання для самостійної роботи учнів.
Перегляд файлу
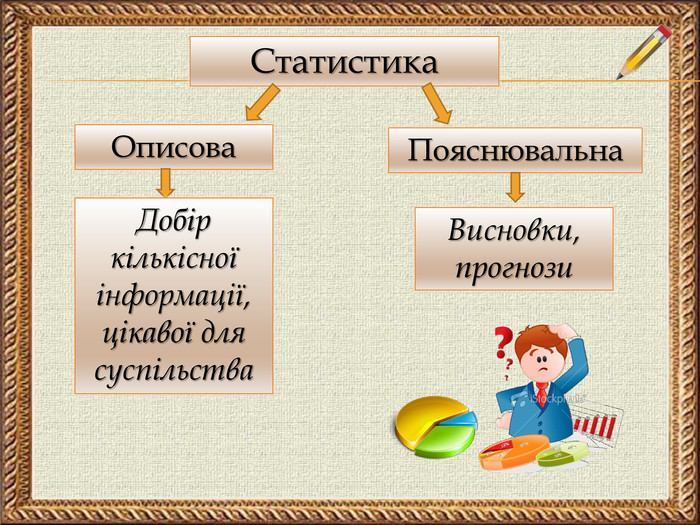
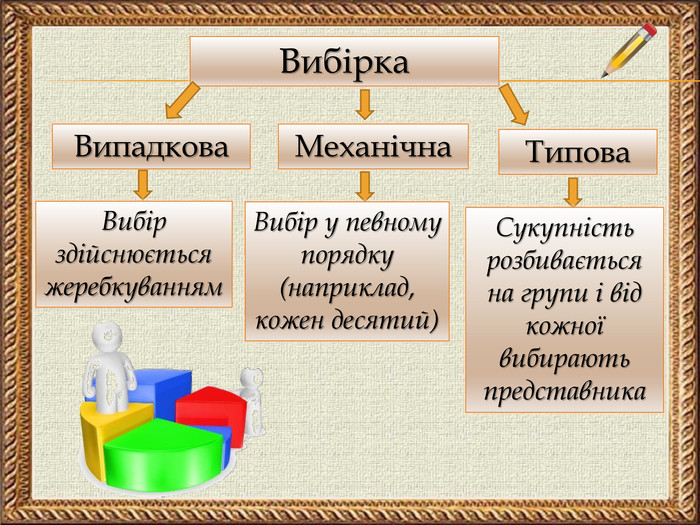
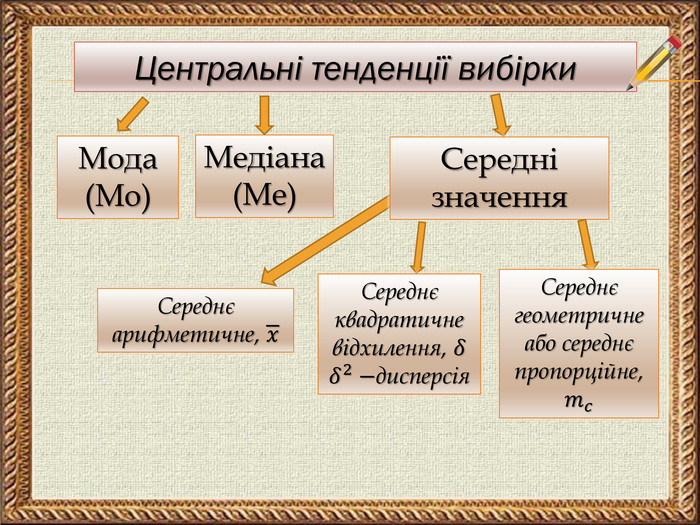
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку































-

П'ятковська Світлана
07.03.2024 в 20:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Якименко Оксана Вікторівна
09.02.2024 в 21:34
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Дунаєвська Ольга
21.01.2024 в 20:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мащакевич Ліана Анатоліївна
14.05.2023 в 11:21
Щиро дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kosyhina Elena
05.04.2023 в 19:27
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мєркулова Ірина
24.05.2022 в 20:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Косенко Вікторія Володимирівна
05.05.2022 в 09:25
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Тимошенко Тетяна Іллівна
04.04.2022 в 00:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Личко Вікторія Михайлівна
07.03.2022 в 20:53
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
10.02.2022 в 10:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гречана Тетяна Іванівна
27.04.2021 в 19:13
Отлично! Большое спасибо!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Павлюк Людмила Петрівна
26.04.2021 в 16:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тиндик Олена
20.04.2021 в 17:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Yeskina Viktoriya
31.03.2021 в 13:21
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Shaga Tanya
14.03.2021 в 00:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ракович Наталія Петрівна
12.01.2021 в 14:04
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Мисюра Тарас
31.10.2020 в 13:30
супер
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тимченко Олена Василівна
23.06.2020 в 19:21
Дякую за цікаву презентацію і за можливість скористатися.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рябіїк Тетяна Олександрівна
07.04.2020 в 21:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Костишена Жанна Павлівна
21.03.2020 в 13:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Букарева Анастасія Анатоліївна
17.11.2019 в 21:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чиновата Зоя Анатоліївна
27.09.2019 в 15:35
Методично грамотно та лаконічно, естетично викладено. Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сердюк Тетяна Борисівна
25.04.2019 в 13:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 20 відгуків