Презентація "Теорія ймовірностей"
Про матеріал
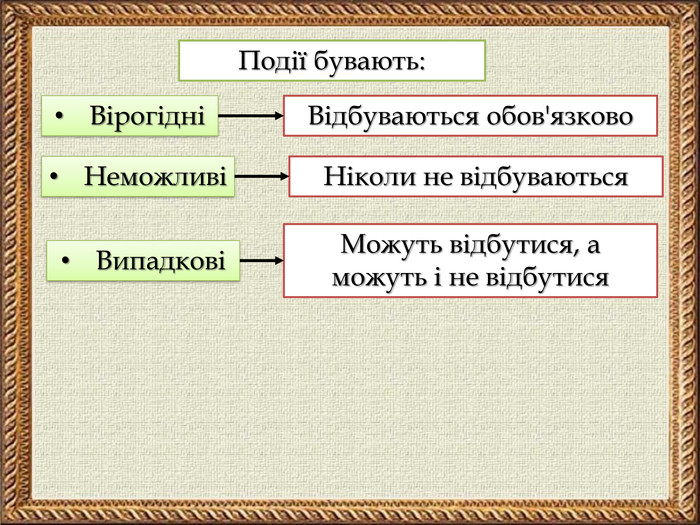
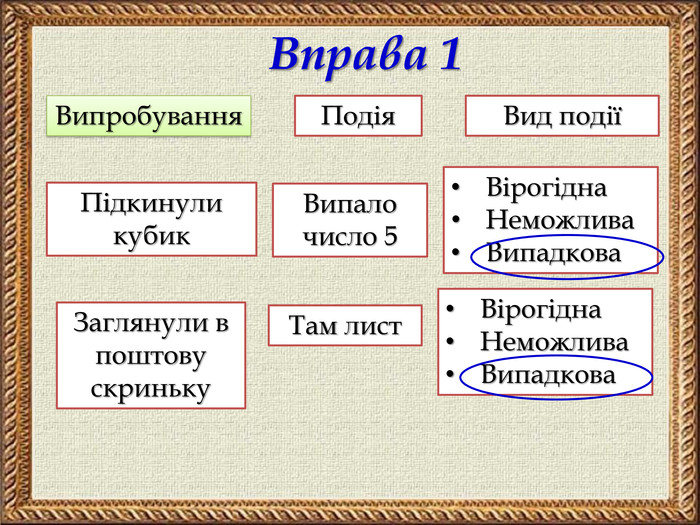
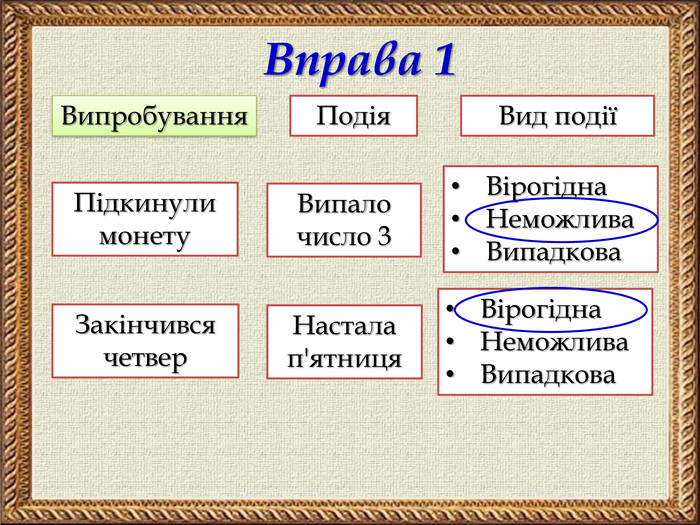
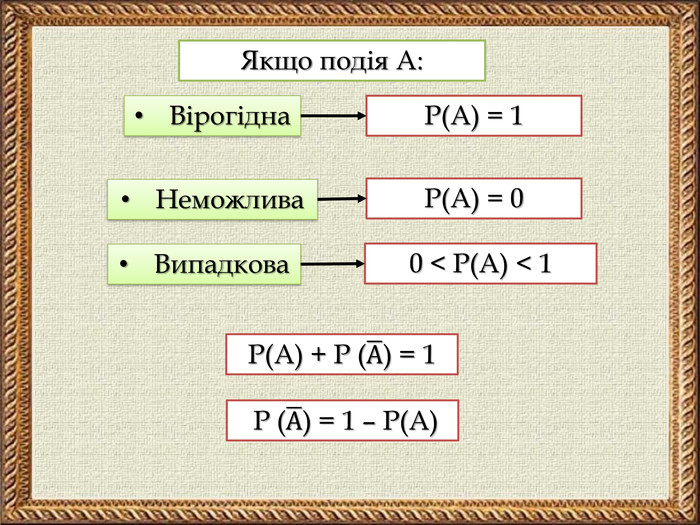
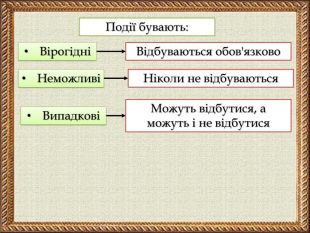
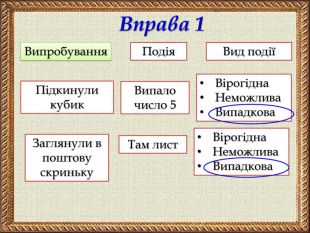
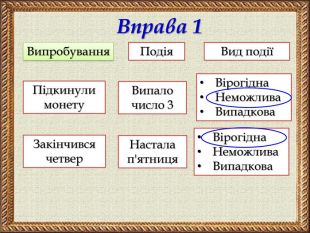
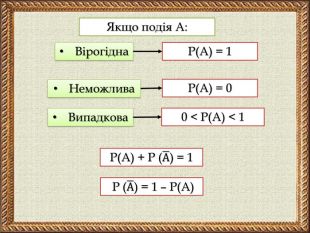
Презентація містить тези основних понять теорії ймовірностей, зразки розв'язування задач на ймовірність та розв'язання складених задач на ймовірність засобами комбінаторики. Покрокова анімація дозволяє учням самостійно опрацьовувати даний матеріал.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку































-

Мащакевич Ліана Анатоліївна
14.05.2023 в 11:24
Загальна:
4.3
Структурованість
3.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жуковська Валентина
23.01.2023 в 22:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
25.09.2022 в 20:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гордєєва Тетяна Миколаївна
11.04.2022 в 10:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мельникова Світлана Олегівна
22.02.2022 в 05:56
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чубарь Елена
01.02.2022 в 23:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Норкіна Олена
03.11.2021 в 16:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
04.05.2021 в 14:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сінченко Тамара Вікторівна
16.04.2021 в 11:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

МАКЕДОНСЬКА ЛЮДМИЛА
15.04.2021 в 19:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чорна Марина Володимирівна
28.03.2021 в 11:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Писаренок Зінаїда Іванівна
24.02.2021 в 08:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Березська Валентина
08.01.2021 в 12:03
Березська Валентина
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Білошапко Наталія Миколаївна
13.04.2020 в 15:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Безродня Ельвіра Євгеніївна
25.03.2020 в 12:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жовмір Олена Олександрівна
21.03.2020 в 09:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Котовський Євгеній
26.02.2020 в 06:01
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Брязкало Юлия
08.12.2019 в 18:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Букарева Анастасія Анатоліївна
17.11.2019 в 21:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
07.05.2019 в 19:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бурдильная Лариса
21.03.2019 в 20:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сердюк Татьяна
26.02.2018 в 09:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 19 відгуків