Конспект уроку з алгебри для 11 класу по темі "Показникові рівняння"

Тема: Показникові рівняння

Мета: ознайомити з означенням показникових  рівнянь та алгоритмом розв’язування цих рівнянь; формувати вміння розв’язувати показникові рівняння;розвивати пам'ять, логічне мислення, культуру математичного мовлення та письма;виховувати старанність, наполегливість, працьовитість.

Тип уроку: засвоєння нових знань, умінь та навичок.

Основні методи та прийоми: словесні, фронтальна бесіда, розповідь, колективне обговорення, самостійна робота,  робота  з підручником, робота в парах.

Обладнання: набір завдань для «мозкового штурму», картки із завданнями, плакат для гри  «Впізнай мене»,  підручник – алгебра 11 клас А.Г. Мерзляк.

                                                    Епіграф уроку:

                                                    Недостатньо мати лише добрий розум,

                                                    Головне - це раціонально застосовувати його.

                                   Рене Декарт

Хід уроку:

І. Організаційний момент.

ІІ. Актуалізація опорних знань.

Два учні працюють з завданнями на картках.

Прийом «Мозковий штурм»

1. Яка з даних функцій є показниковою?  (№ 16.6 ст. 161):

1) у=х⁶                                               3) у=6^х

2) у=                           4) у= 6?

Чому? Яка функція називається показниковою?

Назвіть відомі вам властивості показникової функції.

2. у=2^х, у=0,2^х. Яка з цих функцій зростаюча, а яка спадна?
3. у=2^х  на відрізку 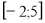. При якому значенні змінної х функція набуває найменшого (найбільшого) значення?
4. Встановіть відповідність. Завдання «пастка».(одна із формул не існує)

Гра «Впізнай мене»

хх	х
х: х
(х)	х
х	х
()	3х

      5. Замініть зірочки, щоб утворилась тотожність (16.1(1,2) ст. 160):

          1) 3⁽⁺¹⁾:3²=3^{*+2+ *}: 3²= 3^{*+2+ * *2}= 3³=27

ІV. Мотивація навчання.

Як бачите, вміння використовувати властивості степеня з довільним дійсним показником, практично полегшує роботу під час розв’язання завдань, спрощення виразів, побудови та читання графіків показникових функцій... . Ці властивості застосовуються досить часто. Сьогодні ми ознайомимось з означенням та алгоритмом розв’язування показникових рівнянь.

ІV. Вивчення нового матеріалу (п.17 ст. 166).

Розглянемо рівняння: 2=8;    3 3=4;    0,3= 0,3

У всіх цих рівняннях зміна міститься тільки в показнику степеня. Наведені рівняння є прикладами показникових рівнянь.

Теорема 17.1. При а 0 і а 1рівність а= авиконується тоді і тільки тоді, коли х= х.(З доведенням та наслідком учні знайомляться самостійно)

Наприклад. 1) 2^х=8,  2^х=2³,  х=3.

2) Якому з наведених проміжків належить корінь рівняння 2^х=?

,

 

V. Закріплення знань та вмінь.

1. Усно. Розв’яжіть рівняння. (робота з підручником) № 17.1 (1,2,6,8) ст.. 170.

1) 4= 64;           2) 3= ;            6) 8= 16;       8) = 25.

2. Розв’язування завдань. (17.3 ст. 171)

1) Робота біля дошки:

Розвяжіть рівняння: а) 3^х=;  б) 5^х+3=()^х; 3) 3+ 3= 90.

2)  робота в парах: хлопці – 2^х+6=()^х; дівчата – 5^х+5^х+1=30.

3) Самостійно – хлопці - № 17.1; дівчата - № 17.3 ст. 170

 

ІV. Підсумок уроку

1. Сьогодні на уроці я вивчив …

                                   пригадав …

                                  запам’ятав…

                                                  зрозумів …

                                                  мені важко давалося …

                                                  тепер буду намагатись …

VІІ. Домашнє завдання

п. 17  ст. 166 (вивчити), виконати № 17.4 (1,2), № 17.6 ст. 171.