В твоїх руках міні-підручник з фізики, 

в якому представлений розділ «Механічна робота та енергія». 

 

Ознайомся зі змістом та очікуваними результатами вивчення теми «Механічна робота та енергія». Для опанування фізики потрібно немало зусиль, уваги: спостерігати фізичні явища, виконувати досліди, розв'язувати задачі, проводити різноманітні вимірювання, осмислювати результати пізнавальних дій.

 

Ти отримаєш величезне задоволення від того, як фізика відкриває перед

тобою все нові й нові можливості: самостійно розбиратись у таємницях і загадках природи, використовувати набуті знання, уміння і навички у повсякденному житті. 

 

Ти дізнаєшся про механічну роботу, потужність, види механічної енергії та закон збереження й перетворення енергії в механічних процесах та його практичне застосування. Зрозумієш, як користуватися простими механізмами для полегшення виконання роботи тощо. Переконаєшся, що у фізиці поняття енергії є основним, а сама фізика є вченням саме про закони взаємоперетворення різних видів енергії. 

 

Щоб полегшити тобі орієнтуватися в тексті міні-підручника і поліпшити засвоєння матеріалу, у

книжці застосовуються такі умовні позначення:

 

 

Відповідаємо на Навчаємося запитання розв’язувати задачі

 

 

                                  Поміркуй і відповідай                                        Це цікаво!

 

Домашній експеримент  

 

 

    

Бажаю  успіхів  у  набутті  знань  про  механічну  роботу  та енергію,  машини  й  механізми, в  оволодінні  вмінням  застосовувати  набуті  знання!

 

 

Зміст 

 

Механічна робота                                                                                                                                                                     .......4

Потужність                                                                                                                                                                                      .......7

Механічна енергія та її види                                                                                                                                          .......9

Закон збереження й перетворення енергії в механічних процесах та його         .....12 практичне застосування

Прості механізми                                                                                                                                                                      .....15

Машини й механізми                                                                                                                                                             .....17

Момент сили. Умови рівноваги важеля                                                                                                              .....18

Лабораторна робота № 11 «Вивчення умови рівноваги важеля»                           .....19

Коефіцієнт корисної дії механізмів. «Золоте правило» механіки                                            .....20

Лабораторна робота № 12 «Визначення ККД похилої площини»                          .....23

«Вічний двигун»                                                                                                     .....24

Навчальний проект «Становлення і розвиток знань про фізичні основи машин .....27

і механізмів»

 

 

Очікувані результати: учень/учениця:

 

Знає й розуміє: 

поняття механічної роботи, потужності, кінетичної і потенціальної енергії, моменту сили, коефіцієнту корисної дії та їхні одиниці, сутність закону збереження механічної енергії, умови рівноваги важеля, «золоте правило» механіки,  принцип дії простих механізмів; 

формули роботи, потужності, ККД простого механізму, кінетичної енергії, потенціальної енергії тіла, піднятого над поверхнею Землі, моменту сили.  

 

Уміє: 

застосовувати набуті знання в процесі розв'язування фізичних задач та виконання лабораторних робіт;  вимірювати ККД простих механізмів; користуватися простими механізмами (важіль, нерухомий та рухомий блоки, похила площина);  пояснювати «золоте правило» механіки. 

 

Виявляє ставлення й оцінює:  прояв закону збереження та перетворення механічної енергії; ефективність використання машин і механізмів

Поняття «робота» у фізиці має певний сенс. Механічна робота  (або робота сили) відбувається в тому випадку, коли відбувається рух тіла під дією сили.

Робота

Механічна робота

 

1. Що таке механічна робота? Слово «робота» у повсякденному житті має багато значень. 

 

            для позначення професії              для оцінки результату праці   для позначення характеру діяльності

 

            для характеристики складності праці   для характеристики стану

Французький учений Віктор Понселе на початку ХІХ століття писав: «Дії, виконувані різними двигунами, нескінченно різноманітні. Щоб мати можливість порівнювати їх між собою, треба ввести величину, що для всіх двигунів служила б загальною мірою». Такою мірою Понселе запропонував уважати добуток сили на переміщення точки її прикладання. Таку величину він назвав механічною роботою.

r

                                                                                                       Якщо напрямок сили F                    r

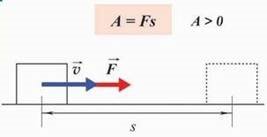
збігається з напрямком переміщення s точки прикладання сили, робота A дорівнює добутку модуля сили на модуль переміщення: A  Fs.

Одиницею роботи, як слідує з визначення, є 1 Дж = 1 H·1м, тобто робота, виконана силою в 1 Н при переміщенні точки прикладання сили на 1 м у напрямку дії сили.

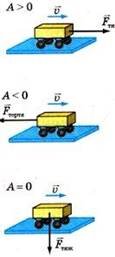
Робота — скалярна величина, але скалярні величини можуть бути позитивними, негативними або рівними нулю. Якщо напрямок руху тіла збігається з напрямком прикладеної сили, то ця сила виконує додатну роботу і її обчислюють за формулою A  Fs.

Якщо напрямок руху протилежний напрямку дії сили, то ця сила виконує від’ємну роботу і її обчислюють за формулою: A  Fs.

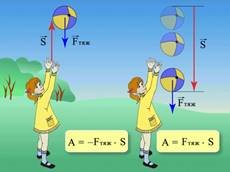
Якщо кинути, наприклад, м’яч вертикально угору, то під час польоту м’яча на нього діє сила ваги, спрямована вниз протилежно переміщенню. Робота сили ваги в цьому випадку від’ємна.

 

2. Коли робота дорівнює нулю?

З формули для роботи сили A  Fs випливає, що у випадку, коли хоча б один зі співмножників (сила F або переміщення s) дорівнює нулю, робота дорівнює нулю — незалежно від величини іншого співмножника.

                                                         якщо переміщення дорівнює нулю

 

    Робота дорівнює нулю            якщо сила перпендикулярна до переміщення

                                                         якщо сила, що діє на тіло, дорівнює нулю

 

Наприклад, якщо м’яч котиться по землі в горизонтальному напрямку, то сила ваги буде перпендикулярна до напрямку руху й роботи не виконає: A = 0. Тіла, що лежать на столі, чинять тиск на стіл, але роботи не виконують. Під час руху планети по круговій орбіті навколо Сонця робота сили притягання дорівнює нулю. Якщо тіло рухається за інерцією, то при цьому не відбувається механічної роботи, тому що в цьому випадку є переміщення, але немає діючої сили.

3. Робота різних сил

а) Робота сили тяжіння

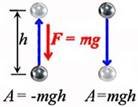
Коли тіло рухається вниз, напрямок сили тяжіння збігається з напрямком переміщення. При цьому робота сили тяжіння додатна й дорівнює нулю: Amgh.

Коли тіло рухається угору, сила тяжіння спрямована протилежно переміщенню. Тому під час руху тіла угору робота сили тяжіння від’ємна й дорівнює Amgh.

 

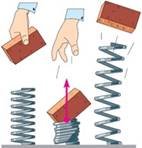
б) Робота сили пружності

Коли стисла пружина розпрямляється,

сила пружності, що діє з її боку, спрямована так само, як переміщення, тому робота сили пружності додатна. При цьому деформація пружини зменшується, тобто при зменшенні деформації сила пружності пружини виконує додатну роботу.

Коли ми стискаємо недеформовану пружину, сила, що діє з боку пружини, спрямована протилежно деформації. Виходить, при збільшенні деформації сила пружності пружини виконує від’ємну роботу.

 

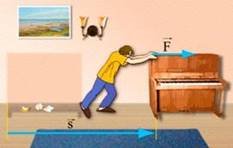
в) Робота сил тертя

Сила тертя ковзання або кочення спрямована завжди протилежно швидкості, а, отже, і переміщенню тіла, тому робота сили тертя ковзання або кочення від’ємна.

У результаті дії сили тяжіння або пружності швидкість тіла може як збільшуватися, так і зменшуватися: у

першому випадку робота додатна, у другому — від’ємна. А в результаті дії сили тертя ковзання або кочення швидкість тіла завжди зменшується: робота цих сил завжди від’ємна.

У розглянутих вище прикладах на тіло діяла тільки одна сила. Якщо на тіло, що рухається, діє кілька сил, то кожна з них може виконувати роботу. При цьому можна підрахувати й роботу кожної з них окремо, й роботу рівнодійної цих сил.

 

1.    Яку фізичну величину називають роботою? 2.    У яких випадках механічна робота дорівнює нулю? Додатна? Від’ємна? Наведіть приклади. 3.    Чому дорівнює робота сили, коли напрямок сили збігається з напрямком переміщення? Коли сила спрямована протилежно переміщенню? 4.    Чи можуть сили, які діють на тіло, що рухається, виконувати одна — додатну роботу, а інша — від’ємну? Наведіть приклад, що ілюструє вашу відповідь.

Горизонтальна сила 8 Н, прикладена до бруска, змушує його рухатися зі  швидкістю 4 см/с. Яку роботу виконала ця сила за 15 с?  Розв’язок. Скористаємося визначенням роботи: A  F l . При цьому  пройдений шлях дорівнює: l t . Остаточно одержуємо: A Ft .  Перевіряємо одиниці величин: A Н м с  Нм  Дж.      с  Обчислюємо роботу: А  80, 0415  4, 8 Дж.

Навчаємося розв’язувати задачі

2.                  Визначте роботу, виконувану при підйомі гранітної плити об’ємом 0,3 м3 на висоту 4 м. 3.                  Людина штовхає візок, прикладаючи горизонтальну силу 50 Н. При цьому візок рухається  рівномірно. Яка його швидкість, якщо за 2 хв виконана робота дорівнює 12 кДж? 4.                  Чи може сила тертя спокою виконувати роботу? Якщо так, наведіть приклад.  Розв’язок. Може. Наприклад, коли людина піднімає вертикально лом, обхопивши його  пальцями, роботу виконує сила тертя спокою, що діє на лом з боку руки.

 

Поміркуй і відповідай

1.                 На пружині нерухомо висить вантаж. Чи виконує роботу сила пружності, що  діє на вантаж? Сила тяжіння? 2.                 Чи виконує роботу сила ваги, що діє на м’яч, коли він: а) лежить на землі; б)  летить у футбольні ворота? 3.                 При рівномірному підйомі вантажу на 10 м виконана робота 1 кДж. Яка вага  вантажу? Яка його маса? 4.                 Вантаж вагою 10 Н рівномірно підняли, виконавши роботу 200 Дж. На яку  висоту підняли вантаж?

 

 Робота якої сили виконується під час руху?

 Придумай за малюнком задачу, запиши в зошит умову

і розв'язування

 

Потужність

 

1. Потужність

Подивись на рисунок: копач й екскаватор почали працювати одночасно. При цьому за однакову кількість часу копач виконав менше роботи. Тому говорять, що потужність екскаватора більше, ніж потужність копача.

Очевидно, потужність більше в тій ситуації, де відбувається більше роботи за той самий час. І, навпаки: потужність менше в тій ситуації, де відбувається менше роботи за той самий час. Отже,  потужність характеризує швидкість виконання роботи й обчислюється за формулою:  A

               N   , де N — потужність, А — виконана робота, t — проміжок часу, за

t

який ця робота виконана.

2. Одиниця потужності

Для вимірювання потужності використовується одиниця ват (Вт). Це потужність, за якої робота в 1 Дж виконується за 1 с:

1^Дж

                                                                                     1 Вт _ .

1с

Одиниця потужності названа ватом на честь англійського винахідника

Джеймса Уатта, що створив першу парову машину. У техніці часто застосовують більші одиниці потужності — кіловат (кВт) і мегават (МВт).

Потужність є важливою характеристикою будь-якого двигуна. Потужності двигунів, створених людиною, можуть коливатися в дуже широких межах: від часток вата (двигун електричної бритви) до сотень і  тисяч мегават (ракетний двигун).

3. Як виразити потужність через силу й швидкість?                         

Потужність транспортного засобу, наприклад, автомобіля,  зручно виражати не через роботу й час, а через силу й швидкість. Нехай тіло рухається з постійною швидкістю й сила, що діє на це тіло, спрямована уздовж переміщення тіла.

A Позначимо модуль швидкості , а модуль сили F. Оскільки N  , а A  Fs, одержуємо:

t

N  Fs  F s  F^t  F, тобто потужність дорівнює добутку сили на швидкість. t t t

1.    Що необхідно знати, щоб визначити виконану роботу, не вимірюючи шлях? 2.    Які одиниці потужності використовуються в техніці? Наведіть приклади. 3.    Чому потужність пов’язана зі швидкістю руху? 4.    Як розрахувати роботу, знаючи потужність?

Під час руху з постійною швидкістю сила тяги двигуна компенсує силу опору руху. Наведена формула для потужності пояснює, чому водій робить перемикання на малу швидкість, коли автомобіль їде нагору по схилу: щоб збільшити силу тяги при тій же потужності мотора, необхідно зменшити швидкість руху.

 

Навчаємося розв’язувати задачі

1.                  Гоночний автомобіль, маса якого 500 кг, розвиває потужність 400 кВт. З якою швидкістю рухається цей автомобіль, якщо сила тяги дорівнює вазі автомобіля?                                                                                                  Fs        s Розв’язок. Відповідно до визначення: N         F     Ft  F.                                                                                                   t          t           t З іншого боку: FPmg .                                                       N      N Звідси одержуємо:               . F mg Перевіряємо одиниці величин:  Вт      Дж  Нм  м . Н сН     сН     с кг кг                                                                                     400 103                  м Обчислюємо шукану швидкість:                    80 .                                                                                      500 10          с 2.                  Кінь тягне віз зі швидкістю 3 м/с, прикладаючи силу 100 Н. Яку потужність розвиває кінь? 3.                  Яку потужність розвиває школяр масою 50 кг, добігаючи з 1-го поверху на 5-й за півхвилини? Висоту поверху прийміть рівною 3 м. 4.                  Двигун автомобіля, розвиваючи потужність 10 кВт, виконав роботу 1,2 МДж. За який час була виконана ця робота? 5.                  Гиря годинника має масу 800 г і за добу опускається на 120 см. Яка потужність такого механізму?

Поміркуй і відповідай

1.                  Два однакових за розміром й конструкцією кораблі розвивають різну  потужність. Чи з однаковою швидкістю будуть рухатися ці кораблі? 2.                  Автомобіль в’їжджає в гору, зберігаючи постійною потужність двигуна. Чому  при цьому зменшують швидкість його руху? 3.                  Чому при розгоні двигун автомобіля розвиває більшу потужність, ніж при  рівномірному русі? 4.                  Першокласник і десятикласник навперегони піднімаються сходами на другий поверх школи. Фінішували вони одночасно. Чи однакову роботу вони виконали? Чи однакову потужність розвивали? 5.                  Збільшується чи зменшується швидкість руху судна щодо води при його переході з ріки в море? Уважайте, що при цьому потужність, яку розвивають двигуни, і число обертів гвинта не змінюються.

Механічна енергія

 

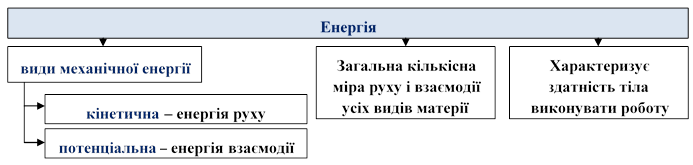
1. Енергія

Розглянемо кілька прикладів, коли роботу виконують сили, що діють з боку деяких тіл.

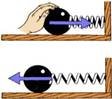
а) При розпрямленні стиснутої пружини сила пружності, що діє з боку

пружини, виконує роботу. Виходить, стиснута (деформована) пружина має здатність виконувати роботу. Цю властивість пружини використовують, наприклад, у пружинних годинниках і заводних іграшках.

б) Вантаж, що опускається з деякої висоти, також виконує роботу:

це використовують, наприклад, у годинниках з гирями й на

гідроелектростанціях, де роботу виконує падаюча з греблі вода.

Отже, піднятий на деяку висоту вантаж має здатність виконувати роботу.

в) Якщо візок, що рухається, зіштовхується з

пружиною, він деформує пружину. Отже, тіло, що рухається, має здатність виконувати роботу.

Про тіла, при зміні стану яких може бути виконана робота, говорять, що вони мають енергію.

 Фізичну величину, що характеризує здатність тіла або системи тіл виконувати роботу, називають енергією. Коли тіло виконує роботу, його енергія зменшується на

величину, рівну виконаній роботі: якщо позначити енергію тіла в початковому стані E_поч, в кінцевому E_кін , а виконану тілом роботу A_т, то E_поч E_кін A_т . Звідси випливає, що одиниця енергії така сама, як й одиниця роботи,— джоуль.

 

2. Потенціальна енергія

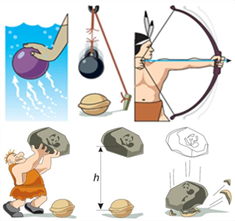
 Спортсмен перед пострілом натягає тятиву лука. Натягнута тятива лука може виштовхнути стрілу, виконуючи при цьому роботу.

Тіло, підняте на деяку висоту над землею, взаємодіючи з нею, так само може при падінні виконати деяку роботу Всі ці тіла мають енергію, тому що взаємодіють з іншими тілами (або частинами тіла).

 Потенціальною енергією називають частину механічної енергії, що обумовлена взаємодією тіл або частин того самого тіла.

Оскільки тіло, підняте відносно поверхні Землі, взаємодіє з нею

(притягується), то воно має потенціальну

енергію Е_п. Будемо вважати потенціальну енергію тіла, що лежить на поверхні Землі, рівною нулю, тоді потенціальна енергія тіла, що перебуває на висоті h, визначається роботою, яку виконає сила ваги при падінні на Землю. А робота може бути визначена за формулою Amgh.

Виходить, у цьому випадку й потенціальна енергія буде виражатися рівністю: E_п  mgh .

Потенціальною енергією володіє будь-яке пружно деформоване тіло. Енергію стиснутих і закручених пружин використовують, наприклад, у ручних годинниках, різноманітних заводних іграшках й ін. 

kx²

           Потенціальна енергія деформованої пружини визначається як E_п   .

2

3. Кінетична енергія

Дуже часто ми бачимо, що механічна робота виконується внаслідок того, що тіло має деяку швидкість.

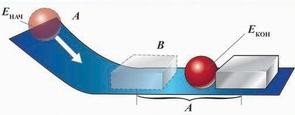
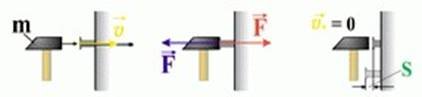
Тепловоз, що рухається, зіштовхуючись із вагоном, переміщає його на деяку відстань. При цьому виконується робота. Коли куля пробиває дошку, також виконується робота. Енергія, якою володіє

тіло, що рухається, називається кінетичною.

 Кінетичною енергією називають частину механічної енергії, що визначається рухом тіла.

Кінетична енергія тіла, що рухається з деякою швидкістю, дорівнює роботі, яку треба виконати, щоб передати тілу в стані спокою таку саму швидкість.

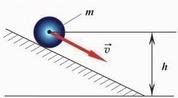
Кінетична енергія E_к тіла масою m, що рухається зі швидкістю υ,

m2

визначається формулою: E_к           . 2

Значення кінетичної енергії залежить від вибору системи відліку: адже кінетична енергія тіла залежить від його швидкості, а швидкість тіла в різних системах відліку різна. Якщо система відліку явно не зазначена, звичайно мають на увазі систему відліку, пов’язану із Землею.

З погляду різних спостерігачів кінетична енергія того самого тіла може бути різною.

 

 

	Механічна енергія
Вид	кінетична	потенціальна
Позначення	ЕК	ЕП
Одиниця вимірювання	Дж
Формула
Властивості	•     Є мірою механічного руху тіл. •     Адитивна величина. •     Скалярна величина. •     Залежить від вибору системи відліку	•    Залежить від взаємного розміщення тіл.  Є функцією тільки координат. •    Фізичний смисл має не саме значення енергії, а різниця енергій. •    Визначена не однозначно, а з точністю до постійної сталої

1.    Наведіть приклади тіл, здатних виконати роботу при переході з одного стану в інший. 2.    Чи змінюється механічний стан тіла або системи тіл під час виконання роботи? 3.    Які тіла мають потенціальну енергію? Наведіть приклади. 4.    Які тіла мають кінетичну енергію? Наведіть приклади.

1.    Вертоліт підняв вантаж масою 1,5 т на висоту 800 м над поверхнею землі. Визначте потенціальну енергію вантажу відносно поверхні землі й відносно дна шахти глибиною 100м. 2.    Швидкість автомобіля збільшилася від 5 м/с до 25 м/с. У скільки разів збільшилася його кінетична енергія? 3.    На яку висоту треба підняти тіло масою 15 кг, щоб потенціальна енергія тіла збільшилася на 45 Дж?

 Навчаємося розв’язувати задачі                                              

 

Закон збереження механічної енергії

 

1. Коли зберігається механічна енергія?

У всіх видів енергії є загальна властивість: енергія нізвідки не виникає й нікуди не зникає, вона лише переходить із одного виду в інший або від одного тіла до іншого. Це твердження називається законом збереження енергії.

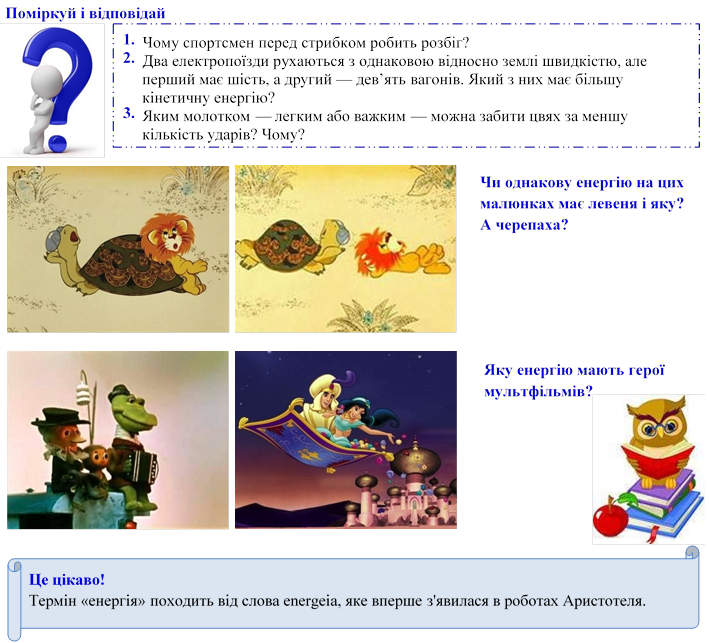
Піднятий над Землею м’яч має певну потенціальну енергію. При його падінні ця енергія поступово зменшується. Однак збільшується його швидкість, що свідчить про збільшення кінетичної енергії. Максимальну кінетичну енергію м’яч має біля самої землі.

Отут його швидкість найбільша, а потенціальна енергія найменша, оскільки висота м’яча наближується до нуля.

Потенціальна енергія піднятого над поверхнею землі м’яча перетворилася на кінетичну енергію м’яча, що рухається. Якщо знехтувати опором повітря, то сума кінетичної й потенціальної енергій падаючого тіла

залишається незмінною, тобто механічна енергія тіла зберігається.

Таким чином, багато явищ природи супроводжуються перетворенням одного виду енергії в інший.

2. Закон збереження механічної енергії

Доведемо, що якщо опором повітря можна знехтувати, сума кінетичної й потенціальної енергій падаючого тіла залишається незмінною, тобто механічна енергія тіла зберігається.

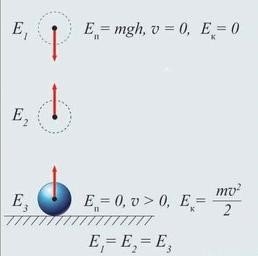
Нехай вантаж масою m падає без початкової швидкості з висоти H.

У початковому стані потенціальна енергія вантажу E_п  mgh , а його кінетична енергія E_к  0.

Таким чином, початкова механічна енергія вантажу E_п  E_к  mgH .

На деякій висоті h  H потенціальна енергія вантажу E_п  mgh . Щоб знайти кінетичну енергію вантажу E_{к } m^2 на висоті h, тобто коли він зробив 2

переміщення S  H h, скористаємося тим, що при вільному падінні без початкової швидкості _{ср ср} ^{  2} 2gS .  Отже, E_к  m²  m 2gS  mgS  mgH h.

S  t ,  _         , а t       , звідки _ 

                                 2            g                                                         2        2

Отже, повна механічна енергія вантажу на будь-якій висоті h  H дорівнює

E_п  E_к  mgh  mgH h mgH , тобто дорівнює його початковій енергії. А це й означає, що механічна енергія при падінні вантажу зберігається.

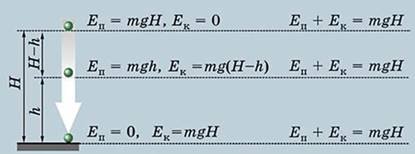Таким чином,

•      механічна енергія зберігається, якщо можна знехтувати тертям, тобто коли на тіло діють тільки сила ваги й сили пружності.

Це твердження називають законом збереження механічної енергії.

Помітимо, що збереження механічної енергії не означає збереження кінетичної й потенціальної енергій окремо: так, при падінні тіла його потенціальна енергія перетворюється в кінетичну, а при коливаннях маятників потенціальна й кінетична енергії неодноразово перетворюються одна в одну.

•      Суму потенціальної й кінетичної енергії тіла називають його повною механічною енергією Е: E  E_п  E_к.

3. Приклади закону збереження механічної енергії

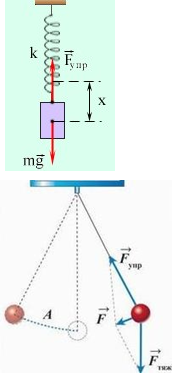 а) Коливання пружинного маятника Вантаж на пружині опустили вниз.

Після відпускання вантажу пружина стискується. У міру її стискання сила пружності пружини зменшується, значить, зменшується й потенціальна енергія пружини. Проте одночасно зростає кінетична енергія вантажу, тому що при розгоні угору збільшується його швидкість. Одночасно зростає й потенціальна енергія вантажу під дією сили ваги, тому що вантаж піднімається вище. У цьому прикладі енергія перейшла з одного виду в інші: з потенціальної під дією сили пружності в кінетичну й потенціальну під дією сили ваги.

б) Коливання нитяного маятника

Відхилимо кульку на нитці вправо й відпустимо: він рухається вліво, збільшуючи швидкість. Отже, кінетична енергія зростає. Одночасно кулька опускається, і в середньому положенні її потенціальна енергія стає найменшою. Однак у цей момент швидкість є найбільшою. Отже, за рахунок запасу кінетичної енергії кулька продовжує рухатися вліво, піднімаючись усе вище. Це призводить до зростання її потенціальної енергії. Одночасно швидкість зменшується, що призводить до зменшення кінетичної енергії кульки.

У цьому прикладі енергія переходила з одного виду в інший: з кінетичної енергії в потенціальну енергію й навпаки.

в) Гальмування тіла силою тертя

На рисунку зображений поїзд, що їде.

Гальмівні колодки притиснулися до колеса. Сила тертя, що виникла між колесом і колодками, сповільнює обертання колеса, а отже, і швидкість поїзда. Під час тертя вони нагріваються настільки сильно, що, торкнувшись рукою, можна одержати опік.

Ми спостерігаємо перетворення енергії з одного її виду в інший й одночасно перехід від одного тіла до інших: кінетична енергія всього поїзда перетворювалася у внутрішню енергію його гальмівних колодок, коліс і

навколишнього повітря. Цей приклад також ілюструє перетворення енергії з одного виду в інший й, одночасно, її перехід від одного тіла до інших.

 

1.    Які перетворення енергії відбуваються при падінні тіла за відсутності опору повітря? 2.    Які перетворення енергії відбуваються під час руху каменя, кинутого угору? 3.    За якої умови зберігається механічна енергія? 4.    Які перетворення енергії відбуваються за наявності тертя?

Навчаємося розв’язувати задачі

 

 

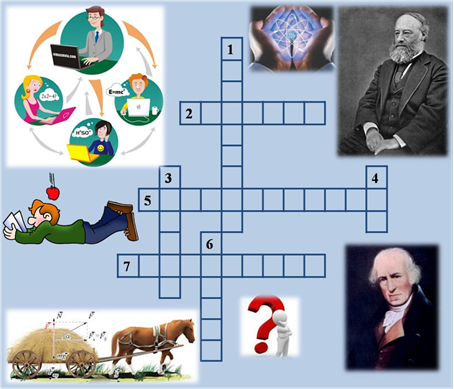
1.             Енергія рухомого тіла.

2.             Фізична величина, що характеризує здатність тіла або системи тіл виконувати роботу.

3.             ... відбувається в тому випадку, коли відбувається рух тіла під дією сили.

4.             Одиниця вимірювання потужності.

5.             Частина механічної енергії, що обумовлена взаємодією тіл або частин того самого тіла.

6.             Одиниця вимірювання механічної роботи.

7.             Фізична величина, яка характеризує швидкість виконання роботи.

 

 

Опиши, які перетворення енергії відбуваються?

 

 

Прості механізми

 

Тисячі років люди працювали, використовуючи переважно силу власних м'язів. Але можливості м'язів людини обмежені. 

Вже в далекі часи виникла потреба мати пристрої, які б дали можливість отримати виграш у силі. Іншими словами, пристрої, застосування яких дає змогу піднімати вантажі, які без таких пристроїв не можна навіть зрушити з місця.

Пристрої, призначені для збільшення сили чи зміни її напрямку, дістали назву механізми. Щоб полегшити свою працю, тобто отримати виграш у силі,

людина винайшла, виготовила та почала використовувати такі прості механізми, як важіль, блок, коловорот, похилу площину, клин, гвинт, колесо та інші. За допомогою таких механізмів люди і будували піраміди, храми тощо. Прості механізми ‒ це не що інше як знаряддя праці. 

Набагато легше переміщувати вантажі, поставивши їх на колеса, колоти кам'яні брили або дерев'яні колоди, користуючись клином ‒ трикутним шматком дерева чи металу. І нині важкі речі, як-от: камені, ящики, навіть автомобілі, людина здатна підняти за допомогою довгого дерев'яного чи металевого стержня або дошки, що мають точку опори, ‒ важеля. За принципом важеля працює криниця, народна назва якої «журавель». Щоправда, важіль має недолік ‒ за допомогою цього простого механізму вантажі не можна підняти на значну висоту.

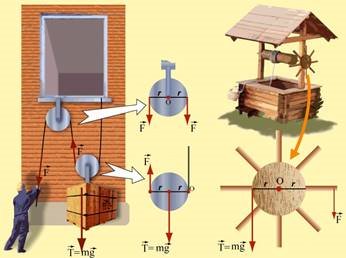
Інший простий механізм ‒ блок не має такого недоліку. Блок виготовляють у вигляді колеса із

заглибиною для мотузки чи ланцюга. Якщо блок закріпити на потрібній висоті і перекинути через нього мотузку або ланцюг, то піднімати вантажі буде зручніше і швидше. Проте блок не дає виграшу в силі, а лише змінює напрямок її дії. Тривалий час цей простий механізм був незамінний у будівництві. Ним і тепер користуються під час індивідуального будівництва.

У сільській місцевості воду з колодязів зазвичай дістають за допомогою коловорота. Це також простий механізм.

До простих механізмів належить і похила площина. Її використовують для отримання виграшу в силі під час переміщення тіл.

 

ü  Прості механізми полегшують працю людини. До них належать важіль, блок, коловорот, похила площина, клин, гвинт, колесо тощо. 

ü  Прості механізми використовують не тільки для виграшу в силі, а й для зміни її напрямку.

ü  Складні механізми створюють, поєднавши два механізми і більше.

 

Характеристики	Прості механізми
	Важіль	Похила площина	Блок
Означення	Тверде тіло, що закріплене на вісі	Площина, що розташована під кутом до горизонту	Деталь у вигляді колеса з жолобом для нитки
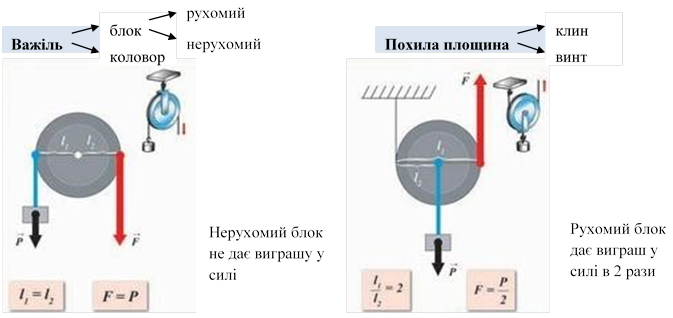
Виграш у силі	разів	разів	Нерухомий блок не дає виграшу у силі. Рухомий блок дає виграш у силі в 2 рази
	У відстані ми програємо у стільки ж разів, у скільки виграємо у силі. Всі прості механізми не дають виграшу в роботі
Використовуються	в механізмах для передачі руху	в побуті та техніці для зменшення навантаження	в будівництві для зміни напряму руху

 

Характеристики		Прості механізми
	Важіль	Похила площина	Блок
Переваги	Виграш у силі, маленька сила тертя	Виграш у силі	Для отримання великого виграшу у силі використовується поліспаст. Зміна напрямку руху
Недоліки	Громіздкість	Громіздкість	Маленький виграш у силі
ККД	середній	найменший	найбільший

 

 

 

 

Як ти можеш пояснити слова Архімеда?

 

 

 

Машини й механізми

 

Пилосос і холодильник, літак і підйомний кран, ткацький верстат і комбайн, велосипед і автомобіль ‒ усе це приклади машин. Зверніть увагу на те, що, незважаючи на відмінності у зовнішньому вигляді та призначенні, матеріалах, з яких їх зроблено, вони мають спільну назву ‒ «машини». Чому? По-перше, тому, що всі вони виконують потрібну людині роботу. По-друге, для її виконання всім машинам потрібна енергія. І по-третє, спільним для всіх машин є наявність трьох основних частин: робочого органа, двигуна і механізму, що їх зв'язує. За відсутності однієї з частин машина не працюватиме. Отже, машина ‒ це система, складові частини якої взаємозв'язані. А оскільки машини створює людина, то їх можна назвати рукотворними системами.

Робочі органи машин можуть бути різними. У гелікоптера ‒ пропелер, у екскаватора ‒ ківш, у велосипеда ‒ колеса. Назва робочий орган свідчить про те, що ця частина допомагає людині виконувати ту роботу, задля якої машину створили.

Призначення двигуна ‒ перетворювати один вид енергії на інший. У двигунах таких машин, як автомобіль, мотоцикл, трактор, хімічна енергія палива перетворюється на теплову, а потім на механічну.  

Двигуни пилососа, пральної машини перетворюють електричну енергію, що надходить до них із електромережі, на механічну. Всі двигуни, зокрема й електродвигуни, під час роботи нагріваються. Це означає, що частина спожитої енергії перетворюється на теплову.

У велосипеда або ручної м'ясорубки двигуна немає. Чому ж їх також називають машинами? Тому що роль двигуна у них відіграє людина, витрачаючи на виконання роботи свою енергію.

Робочий орган і двигун з'єднані між собою механізмом. У багатьох машин ‒ це прості механізми (важіль, блок, ланцюг, пасок) або їх поєднання. Так, механізм велосипеда є поєднанням таких простих механізмів: важіль, вісь, зубчасте колесо (шестерня), ланцюг.

ü Машини ‒ це пристрої, що виконують корисну для людини роботу і при цьому перетворюють один вид енергії на інший. 

ü Основними частинами кожної машини є робочий орган, двигун, механізм.

ü Сучасні машини ‒ це величезне досягнення людини, що стало можливим завдяки її невтомним пошукам і праці.

ü У машинобудуванні використовують метали, пластмаси, гуму, скло та багато інших речовин і матеріалів.

Момент сили. Умови рівноваги важеля

 

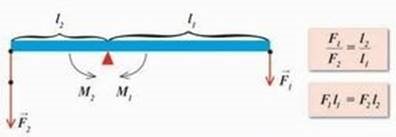Важелем називають тверде тіло, що може обертатись навколо будь-якої нерухомої опори. Найбільш коротша відстань між точкою опори та прямою, вздовж котрої діє на важіль сила, називають плечем сили.

Добуток модуля сили, яка обертає тіло, на плече її називають моментом сили; він позначається літерою М.

М = F l Важіль знаходиться в рівновазі під дією двох сил, коли момент сили, яка його обертає за годинниковою стрілкою, рівна моменту сили, яка його обертає проти годинникової стрілки. Дане правило називають правилом моментів, що записується у вигляді формули. M1 = M2

 

1.    Якщо вісь обертання важеля розміщена посередині і до кінців важеля прикладені однакові сили, спрямовані в одну сторону, то …  a) важіль знаходиться в рівновазі; b) важіль повернеться 2.    Якщо вісь обертання важеля розміщена посередині і до кінців важеля прикладені неоднакові сили, спрямовані в одну сторону, то … a) важіль знаходиться в рівновазі; b) важіль повернеться 3.    Якщо вісь обертання важеля розміщена посередині і до кінців важеля прикладені однакові сили, спрямовані в протилежні сторони, то …  a) важіль знаходиться в рівновазі; b) важіль повернеться

 

Навчаємося розв’язувати задачі 

 

 

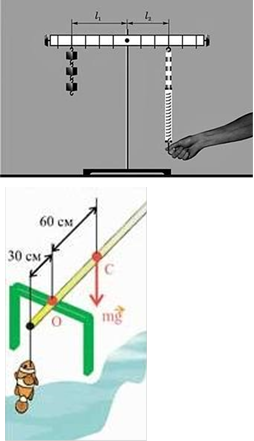
1.  Яку силу необхідно прикласти до другого плеча, щоб важіль був зрівноважений? Один тягарець має масу 100 г, а одне ділення на важелі

‒ 10 см.

 

 

 

 

2.  Як за допомогою вудки, маса якої 1 кг, визначити масу рибки?

 

 

 

 

 

 

 

 

 

Лабораторна робота № 11 «Вивчення умови рівноваги важеля»

 

Мета роботи: перевірити на досліді умови рівноваги важеля.

Обладнання: штатив з муфтою, важіль, набір важків, динамометр, лінійка з міліметровими поділками.

 

Теоретичні відомості 1. Установіть важіль на штативі й зрівноважте його в горизонтальному положенні за допомогою регулювальних гайок на кінцях.

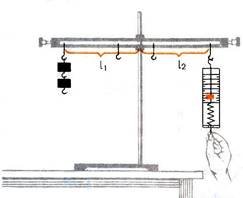
2.         Утримуючи рукою важіль у горизонтальному положенні, підвісьте до нього на довільній відстані від осі «гірлянди» важків загальною вагою Р, як показано на рисунку.

3.         Зрівноважте важіль, прикладаючи до нього за допомогою динамометра вертикально спрямовану силу, як показано на рисунку. Виміряйте модуль цієї сили F.

4.         Визначте за допомогою поділок на важелі плечі сил l₁ й l₂ (див. рисунок).

5.         Повторіть дослід ще два рази, змінюючи положення точок підвісу важків й їхню загальну вагу.

6.         Зробіть у зошиті для лабораторних робіт схематичні рисунки дослідів. На рисунках укажіть прикладені до важеля сили й плечі цих сил. Обчисліть моменти М1 і М2 сил, які обертають важіль відповідно проти годинникової стрілки й за годинниковою стрілкою.

7.         Заповніть у зошиті наступну таблицю:

 

	№ досліду	P , Н	l1 , м	M1 , H·м	F , Н	l2 , м	M2 , H· м
	1
	2
	3

8.         Порівняйте значення моментів М₁ і М₂ сил, які обертають важіль у протилежних напрямках і

зробіть висновок. 

 

 

 

 

 

 

 

 

«Золоте правило» механіки. ККД

 

1. «Золоте правило» механіки й закон збереження енергії

Давно пройшов той час, коли будь-яку роботу людина мала виконувати безпосередньо своїми руками. Зараз піднімати вантажі, переміщати їх по землі, воді й у повітрі, виконувати будівельні роботи й багато чого іншого людині допомагають механізми. На зорі розвитку цивілізації людина для своєї діяльності використовувала прості механізми — важіль, блок, похилу площину, клин, коловорот.

З їх допомогою були створені унікальні спорудження, деякі з яких збереглися до наших днів.

І сьогодні прості механізми мають широке застосування як самі по собі, так і як частини складних механізмів.

При використанні простих механізмів можна одержати виграш у силі, але він неодмінно супроводжується програшем у переміщенні. Можна й, навпаки, одержати виграш у переміщенні, але тоді ми неодмінно програємо в силі. Архімед установив на досліді, що 

•      при використанні простих механізмів ми або виграємо в силі в стільки разів, у скільки разів програємо в переміщенні, або виграємо в переміщенні в стільки разів, у скільки разів програємо в силі.

 Це твердження назвали «золотим правилом» механіки. Найбільш чітко його сформулював Галілей, уточнивши, що воно справедливо, коли тертям можна знехтувати.

Довгий час «золоте правило» механіки розглядалося як «самостійний» закон природи. І тільки після відкриття закону збереження енергії з’ясувалося, що «золоте правило» механіки є одним із проявів закону збереження енергії:

•      при використанні будь-якого простого механізму не можна одержати виграш у роботі. Із закону збереження енергії випливає й набагато більш загальне твердження, що стосується будьяких механізмів,— не тільки простих, але і як завгодно складних: неможливе існування так званого «вічного двигуна», призначенням якого було б вічно виконувати роботу без витрати енергії.

 

2. Коефіцієнт корисної дії

Практично в будь-якому механізмі, у кожній машині діє сила тертя, на подолання якої витрачається частина енергії, що передається механізму. Ця частина енергії перетворюється у внутрішню, тобто вона йде на нагрівання тіла. Отже, механізм передає лише частину енергії, отриманої ним від іншого тіла, тому тілу, яке він пересуває.

Робота, що виконується над механізмом для приведення його в рух, називається виконаною або повною роботою.  

Нехай тіло піднімають по похилій площині, прикладаючи силу F, спрямовану уздовж площини.

Робота цієї сили є витраченою (або повною).

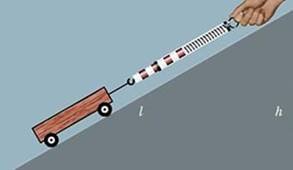Робота, що виконується механізмом над переміщуваним тілом, називається корисною роботою. При рівномірному підйомі тіла по похилій площині сила F, спрямована уздовж площини, переміщаючи брусок на відстань l, виконує роботу A_вик  Fl .

При підйомі тіла масою m на висоту h виконується корисна робота A_к  mgh .

Для визначення ефективності механізму треба знати, яку частину витраченої роботи становить корисна робота. Із цією метою вводять коефіцієнт корисної дії (ККД).

 Коефіцієнтом корисної дії називають відношення корисної роботи A_к до витраченої A_вит A^к η       .

Aвит

Коефіцієнт корисної дії часто виражають у відсотках, наприклад, η = 0,7 можна записати також у вигляді η = 70 %.

У більшості випадків корисна й витрачена роботи виконуються протягом однакового часу. Тому ККД можна обчислювати через повну й корисну потужності.

                                                                          A^к                                       N^кt                                  N^к

                                                               η  100%  100%          η  100%

                                                                        Aвит                                 Nповнt                              N

              ^повн

Із «золотого правила» механіки випливає, що корисна робота дорівнює витраченій. Але це виконується тільки за ідеальних умов: важелі й блоки невагомі й у них, а також на похилій площині немає тертя. У разі невиконання цих умов корисна робота завжди буде менше, ніж витрачена (повна). Тому ККД завжди менше 100 %.

Усяку машину прагнуть зробити такою, щоб її ККД наближався до одиниці. Для цього зменшують, наскільки можливо, силу тертя й інші втрати в машині.

 

1.    Чому важіль не дає виграшу в роботі? 2.    Чому блок не дає виграшу в роботі? 3.    Яку роботу називають корисною? 4.    Яку роботу називають витраченою (або повою)? 5.    Чому корисна робота на практиці завжди менше витраченої? 6.    Що показує ККД? Як можна збільшити ККД?

 

Навчаємося розв’язувати задачі

1.                  По похилій площині піднімають вантаж масою 60 кг, прикладаючи до  нього силу 250 Н, спрямовану уздовж площини. Чому дорівнює ККД  площини, якщо її довжина дорівнює 10 м, а висота дорівнює 3 м?  Розв’язок. Корисна робота Aк  mgh , де m — маса вантажу, h — висота  похилої площини. Витрачена ж робота Aвит  Fl , де F — прикладена сила, l    — довжина похилої площини. Отже,                                                          η Aк  mgh .                                                              Aвит              Fl  Перевіривши одиниці величин і підставивши числові дані, одержимо:         609,83  η  25010  0,71. Таким чином, у цьому випадку ККД становить 71%. 2.                  За допомогою важеля підняли вантаж масою 100 кг на 1 м. При цьому  сила, прикладена до іншого плеча важеля, виконала роботу 1,5 кДж. Чому  дорівнює ККД важеля?

 

Поміркуй і відповідай

 

 

Розгадай  

1.                  Цей механізм не дає виграшу в силі, а лише змінює напрямок її дії.

2.                  Це такий простий механізм, за допомогою якого у сільській місцевості зазвичай дістають воду з колодязів. 

3.                  За допомогою якого простого механізму вантажі не можна підняти на значну висоту.  4.     По горизонталі: пристрій, призначений для збільшення сили чи зміни її напрямку.  

По вертикалі: пристрій, що виконує корисну для людини роботу і при цьому перетворює один вид енергії на інший.

5.        Цей вчений найбільш чітко сформулював «золоте правило» механіки. 

6.        Його використовують щоб колоти кам'яні брили або дерев'яні колоди. 

7.        Кому із вчених належать слова «Дайте мені точку опори і я зрушу Землю»?  

8.        Одна із основних частин машин. 9. Вона потрібна для виконання роботи всім машинам.

 

Придумай за малюнками задачі, запиши в зошит умову і розв'язування

 

 

 

 

 

 

 

 

 

Лабораторна робота № 12 «Визначення ККД похилої площини»

 

Мета роботи: Вивчити властивості похилої площини в експериментальних умовах і визначити її ККД.

 

Обладнання: гладенька дошка завдовжки 50 см, дерев'яний брусок, динамометр, набір важків масою по 100 г кожний, штатив з лапкою, мірна стрічка.

 

Теоретичні відомості

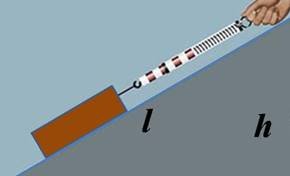
У техніці, на виробництві і в повсякденному житті застосовують простий механізм, який має назву похилої площини. Це пристрій, у якому довга дошка чи рейка покладені так, що утворюють деякий кут із горизонтом.

Як правило, цей кут менший за 45°.

Використання похилої площини дає змогу дістати виграш у силі. Виграш у роботі, як стверджує «золоте правило» механіки, отримати не можна. У реальних

умовах той, хто користується похилою площиною, навіть програє в роботі, оскільки при переміщенні тіла похилою площиною виконує додаткову роботу з переборення сил тертя.

 

Виконання роботи  1. Кінець дошки закріпіть в лапці штатива так, щоб вона утворювала кут 15...20° з горизонтом.

Виміряйте довжину дошки і висоту закріпленого кінця дошки над поверхнею стола.

2.      Виміряйте вагу дерев'яного бруска.

3.      Навантаживши брусок важком масою 100 г, покладіть його на дошку.

4.      До бруска приєднайте динамометр і почніть його тягти рівномірно вгору похилою площиною, стежачи за показами динамометра.

5.      Повторіть дослід із бруском, навантаженим спочатку двома, а потім трьома важками.

6.      Розрахуйте ККД похилої площини і виграш у силі для кожного із трьох дослідів.

7.      Результати вимірювань і розрахунків запишіть у таблицю.

 

№ досліду	l , см	h , см	F , Н	mg , Н	Aвит , Дж	Aк , Дж	η , %
1
2
3

 

8.      *Збільшіть висоту закріпленого кінця дошки і повторіть дослід згідно з п. 1-6. Порівняйте значення ККД для обох випадків і зробіть висновки щодо залежності ККД і виграшу в силі від кута нахилу похилої площини.

9.      Дослідіть отримані результати й з’ясуйте: чи одержуємо ми виграш у силі? у роботі? Як ваша відповідь узгоджується із «золотим правилом» механіки?

 

 

 

 

Вічний двигун

 

1. Від великої омани до великого відкриття  

По небу вічно рухається Сонце, Місяць і планети, вічно обертається навколо своєї осі Земля... Вічно течуть ріки, і вічно біжать гнані вітром хмари... Люди навчилися навіть використовувати вічний рух води й вітру, побудувавши водяні й вітряні млини.

Тому не дивно, що розумами вчених й інженерів заволоділа зухвала думка: якщо вічний рух існує в природі, виходить, і людина може створити вічний двигун і змусити його служити собі.

Міркування про створення вічного двигуна не давали спокою багатьом, навіть видатному італійському художникові й винахідникові Леонардо да Вінчі.

Чи слід всякого, хто в минулі століття намагався побудувати вічний двигун, уважати неуком чи божевільним?

З розвитком виробництва потреба у двигунах дедалі збільшувалася, а теплових двигунів ще не було. А після того, як їх винайшли, вони тривалий час залишалися занадто дорогими. Знаменита картина художника Іллі Рєпіна показує, як важко було обходитися без двигунів.

Однак всі спроби створити вічний двигун завжди закінчувалися невдачею. Учені й інженери довго не помічали принципового розходження між вічним рухом і вічним двигуном.

Вічний рух можливий, якщо повністю усунути тертя — таким, наприклад, є рух за інерцією, коли на тіло не діють інші тіла.

Однак вічний двигун, тобто пристрій, що виконував би роботу без споживання енергії,

неможливий навіть за повної відсутності тертя.

Сьогодні ми знаємо, що це — наслідок закону збереження енергії. Але, як ми незабаром побачимо, цей великий закон зобов’язаний своїм відкриттям... саме вічним двигунам, що не відбулися.

Але чи були даремними всі спроби побудувати вічний двигун? Ні! Невдачі спонукали вчених по-новому глянути на проблему, що й призвело, зрештою, до відкриття закону збереження енергії.

2. Загадки й розгадки «вічних двигунів»

Найдавніший з відомих на сьогодні проектів вічного двигуна належить індійському поетові, математикові й астрономові Бхаскаре, що жив в ХІІ столітті. Він пропонував на колесі закріплювати довгі закриті посудини, наполовину наповнені ртуттю. 

Посудини розташовувалися під кутом до радіуса колеса, тому при будь-якому положенні колеса в його лівій частині перебуває більше

ртуті, ніж у правій. Отже, за задумом «винахідника», колесо має обертатися

проти годинникової стрілки.

У чому полягає помилка проекту?

У правій частині колеса ртуті, дійсно, менше, ніж у лівій, але ж ця ртуть перебуває далі від осі.

Розрахунок показує, що моменти сил, з якими діє на колесо ртуть у лівій і правій частині колеса, у точності врівноважують один одного. І тому внаслідок правила моментів колесо буде перебувати в рівновазі.

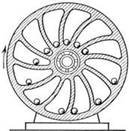Приваблива ідея побудувати колесо, що не може перебувати в рівновазі й тому обертатиметься вічно, прямує крізь століття, підкоряючи одну країну за іншою.

Таким, наприклад, був один із проектів Леонардо да Вінчі. Як і всі інші, цей «вічний двигун» не працював, але виглядав гарніше за інші — адже його творцем був не тільки великий винахідник, але й великий художник.

У чому полягає помилка проекту?

Якщо підрахувати, скільки кульок знаходиться з кожної сторони колеса, то

виявиться, що ліворуч кульок більше. Розрахунок показує, що моменти сил, що обертають колесо в протилежні сторони, у точності рівні.

Як ми бачимо, більш пізні винахідники «вічних коліс» наводили докази, протилежні аргументам перших винахідників — тепер вони віддавали перевагу не силі, а плечу сили, але ще не вміли правильно знаходити моменти сил.

 

3. Користь від пошуку вічних двигунів все-таки була!

Великий італієць Леонардо да Вінчі, що присвятив винаходу вічного двигуна багато років, з кожним новим проектом дедалі глибше осягав проблему, що стояла перед ним. Зазнавши невдачі з будовою «вічного колеса» (про цей його проект ми розповіли вище), він уперше робить точний розрахунок моментів сил для «вічного колеса».  

Ось його висновок: «сумарний момент сил, що обертають колесо в одну сторону, у точності дорівнює сумарному моменту сил, що обертають колесо в іншу сторону. Тому існування «вічного колеса» неможливо». Це — перший науково обґрунтований висновок про неможливість вічного двигуна.

 Однак головний висновок стосовно неможливості створення вічного двигуна зробив Роберт Майєр. Він писав, що роздуми й нові спостереження й призвели його до відкриття закону збереження енергії.

 Герман Гельмгольц, інший із учених, що відкрили закон збереження енергії, також говорив, що на думку про збереження енергії його навели багатовікові невдалі спроби створити вічний двигун.

 

 

Навчаємося розв’язувати задачі

 

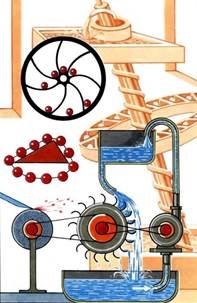
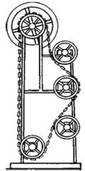
1.  Може видатися, що права, довша, частина ланцюга, повинна постійно переважувати ліву, коротшу частину, внаслідок чого ланцюг має вічно обертати колеса, призводячи до руху певний механізм. У чому помилка проекту?

 

 

 

 

2.  За задумом автора проекту, зображеного на рисунку, колесо буде обертатися вічно, оскільки чотири молоточки завжди будуть переважувати три таких самих молоточки. У чому помилка проекту?

3.  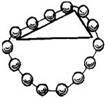Наприкінці XVI століття нідерландський математик й інженер Симон Стевін пропонує розглянути ланцюжок з однакових кульок на двох похилих площинах. У чому помилка проекту?

 

Розв’язок. Може видатися, що дві кульки на правій площині не можуть урівноважувати чотири кульки на лівій площині, і тому ланцюжок має вічно обертатися (проти годинникової

стрілки). Але дослід свідчить, що ланцюжок перебуває в рівновазі. І тоді, виходячи з неможливості вічного двигуна, Стевін знаходить умови рівноваги тіл

на похилій площині.

 

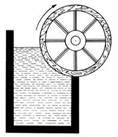
4.  Обертовий на осі дерев’яний барабан частково занурений у воду. За задумом авторів «винаходу», на занурену у воду частину барабана діє, відповідно до закону Архімеда, виштовхувальна сила, спрямована угору. Тому барабан повинен вічно обертатися. У чому помилка проекту?

 

Розв’язок. Сили тиску води спрямовані перпендикулярно до поверхні барабана, тобто спрямовані до осі барабана. Тому ці сили не обертають барабан, а тільки намагаються викривити

вісь, на яку він посаджений.

 

5.  Один з проектів «вічного двигуна». Чому він не буде працювати?

 

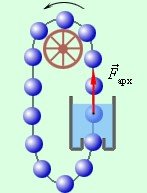
Що ще тобі відомо про «вічний двигун»? Поділись інформацією  

 

 

Навчальний проект  «Становлення і розвиток знань про фізичні основи машин і механізмів»

 

 

 

 

Вимоги до навчального проекту

 

Ø  Необхідна наявність значущої в дослідницькому, творчому плані проблеми.

Ø  Робота над проектом розпочинається з планування дій щодо розв’язання проблеми.

Ø  Самостійна дослідна діяльність учнів.

Ø  Результати виконаних проектів повинні бути матеріальні (відеофільм, презентація, альбом,

комп'ютерна газета, альманах тощо). 

 

 

 

              Світ машин та механізмів тепер супроводжує

 

                              людину на кожному кроці. 

          Людина, суспільство стають все більш залежними

                           від сучасної, складної техніки

 

 

 

 

 

 

 

 

 

Джерела:

 

 

 

 

1.      Іванова Ж.В. Фізика. 8 клас. Розробки уроків. Харків "Ранок. Веста", 2008

2.      Кара Ф.М. Роєва Т.Г. Фізика. 8 клас. Завдання для тематичного оцінювання. Харків "Країна мрій", 2008

3.      Кирик Л. А. Усі уроки фізики. 8 клас — Х.: Вид. група «Основа», 2008

4.      Кононіченко С.П. Роєва Т.Г. Фізика. Навчальний посібник. 8 клас. Харків "Країна мрій", 2008

5.      Пивовар Л.М. Роєва Т.Г. Фізика. 8 клас. Актуальні уроки. Харків "Країна мрій", 2008

6.      Навчальна програма з фізики для 7-9 класів підготовлена робочою групою у складі:

О.І. Ляшенко, доктор педагогічних наук, професор, академік НАПН України (керівник групи);

В.Г. Бар’яхтар, доктор фізико-математичних наук, професор, академік НАН України; Л.Ю. Благодаренко, доктор педагогічних наук, доцент; М.В. Головко, кандидат педагогічних наук, доцент; Ю.І. Горобець, доктор фізико-математичних наук, професор, член-кореспондент НАПН України; Т.М. Засєкіна, учитель фізики, кандидат педагогічних наук; В.Д. Карасик, учитель фізики, Заслужений учитель України, переможець Всеукраїнського конкурсу "Учитель року-2005"; О.В. Ліскович, завідувач лабораторії Миколаївського ОІППО;

М.Т. Мартинюк, доктор педагогічних наук, професор, член-кореспондент НАПН України;

І.Ю. Ненашев, учитель фізики, лауреат Всеукраїнського конкурсу "Учитель року-1996"; Н.А. Охрименко, методист Донецького ОІППО; В.Д. Сиротюк, доктор педагогічних наук, професор; М.І. Шут, доктор фізико-математичних наук, професор, академік НАПН України.

2012 р.

7. Сайти: festival.1september.ru, ifizik.ru