Міні-підручник з теми "Раціональні числа та дії над ними"

Дорогі шестикласники!

 Цей міні-підручник допоможе вам у вивченні теми «Раціональні числа та дії над ними». Опрацювавши його, ви навчитеся додавати, віднімати, множити та ділити раціональні числа. Також дізнаєтеся, що таке коефіцієнт, як розкрити дужки у виразі та як звести подібні доданки.

Основні положення тем стисло викладені у схемах, таблицях, пам’ятках. До них відразу наведені приклади. На допомогу  у роботі за цим підручником є система умовних позначок:

 

	зосередься, поміркуй та запам’ятай
	навчись правильно записувати розв’язання
	дізнайся більше про історію математики
	потренуйся у виконанні вправ
	перевір свої знання

 

Тренувальні вправи розподілені за рівнем складності: 

-  завдання початкового рівня складності; 

-   завдання середнього та достатнього рівня складності;     

-   завдання високого рівня складності. 

  Для тих, хто хоче знати більше

 

Розв’язування багатьох задач, особливо тих, які розв’язуються за допомогою рівнянь, призводило до віднімання від меншого числа більшого. Це вимагало введення нових чисел.

Вперше від’ємні числа з’явилися у Давньому Китаї приблизно 2100 років тому. Там вміли додавати та віднімати додатні та від’ємні числа.

В Індії у VII ст. були вже відомі правила множення та ділення від’ємних чисел. У Європі від’ємними числами почали користуватися в ХІІ-ХІІІ ст.. Але більшість учених ставилися до них, як до «хибних», а до додатних – як до «справжніх».

Завдяки французькому математику, фізику та філософу Рене Декарту (1596-1650 рр.) додатні та від’ємні числа отримали геометричне трактування. Він увів координатну пряму(1637р.).

Загальне визнання від’ємні числа як дійсно існуючі отримали лише у першій половині ХУІІ ст.. Тоді ж затвердилося й сучасне позначення для від’ємних чисел.

 

 

          § 1. Додавання раціональних чисел

 

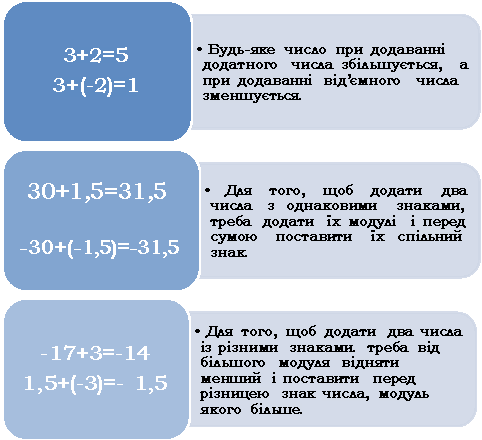
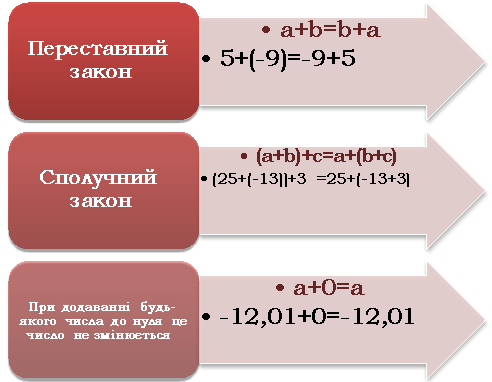
           §2. Властивості додавання

Зразок

1.Знайдіть суму чисел:

 (-13)+(-15)+(+9)+(-17)

Застосуємо переставний та сполучний закони додавання:

 ((-13)+(-17)+(-15))+9=-45+9=-36

 

2. Обчисліть: -3

-3 - 3.

 

3. Знайдіть суму: -6,4+5,1;    -5,8+7,2.

-6,4+5,1=-(6,4-5,1)=-1,3

-5,8+7,2=(7,2 – 5,8)=1,4

Запитання для самоперевірки

1. Вибудуй послідовно відповідь:

Щоб додати два від’ємних числа, потрібно

     -    їх                                  -    поставити

     -    додати                         -    перед

         -    модулі                         -    сумою

         -    мінус                                -    знак

1. Як додати два числа з різними знаками?
2. Чому дорівнює сума двох протилежних чисел?
3. Назвіть основні властивості додавання.
4. Чи вірно, що сума будь-яких двох чисел більша від кожного з доданків? Наведіть приклади, які підтверджують або спростовують це твердження.

 

Тренувальні вправи

1. 1. Знайдіть суму чисел

-20+(-15);                    -0,5+0,25;

-4,8+(-6,12);                ;

- 0,3 - 0,7;                   -110+(-120).       

2. Виконайте додавання

-7+11;                      0,6+(-0,4);

-119+16;                 128+(-128,3);

0,001+(-0,01);         (-4,5)+144,5.

3. Знайдіть значення виразу

27,8+(-43,08);          -3,97+(-4,3);

-11,56+(-56,09);      -8,9+6,7;

-8,9+(-6,7);              0,45+(-1,05).

4. Виконайте додавання

;                

;        - 1 +

      

5. Обчисліть

(1,8)+(-2,6)+0,37;    14+(-23)+19+(-11);

.

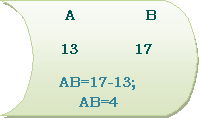
           §3. Віднімання раціональних чисел

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

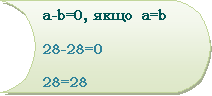
Для тих, хто хоче знати більше

Індійські математики уявляли собі додатні числа як «маєтність», а від’ємні числа як борги. Індійські математики Брахмагупта (УІІ ст.) і Бхаскара (ХІІ ст) так формулювали правила додавання та віднімання: «Сумою двох маєтностей є маєтність. Сума маєтності та боргу дорівнює їх різниці. Сума двох боргів є борг. Сума майна і такого самого боргу дорівнює нулю».

 

Зразок

1. Знайдіть різницю: 12-(-4);

                                       -15-(-10).

Розв’язання: 12-(-4)= 12+4=16;

                       -15-(-10)=-15+10=-5

2. Температура повітря за день знизилася на 6 і до кінця дня стала дорівнювати -10. Якою була температура повітря вранці?

Розв’язання: температура повітря вранці - х, зниження на 6 позначимо -6. Тоді, х+(-6)=-10;    

 х=-10-(-6); х=-10+6; х=-4.

Завдання для самоперевірки

Поставте знак «+», якщо твердження вірне, або «-», якщо воно не вірне.

1. Для того, щоб від даного числа відняти інше, треба до від’ємника додати число, протилежне зменшуваному.
2. Різниця двох чисел додатна, якщо зменшуване більше від’ємника.
3. Різниця двох чисел від’ємна, якщо зменшуване менше від’ємника.
4. Різниця двох чисел дорівнює нулю, якщо зменшуване більше від’ємника.

Тренувальні вправи

1. Обчисліть

-887 – 113;                            475 – (-109);

-5810 – (-6326);                    6,28 – (-3,72);

-9,64 – (2,36);                       4,07 – 6,38.

 

2. Запишіть вираз у вигляді алгебраїчної суми та обчисліть

-184 - (-107) - (+216) - (-144)+(-208);

(-1,485) - (-3,087)+(-2,408)+(-1,005).

3. Виконайте дії

3,7 + (-8,3) – (-2,8)+(-4,3));  

         -0,76 – (-0,55+(-0,77)+0,92);

        -7,5 – (-4,8) – (-3,3 – 1,7).

 

4. Розв’яжіть рівняння

х – (-8) = 3;                             -11 – х =7;

-5,4 – х = 1,6;                         -0,84 – х = -0,34;

-8 – х = 13,1;                          х – (-3 - 9) = -17,2.

 

5. Висота гори Еверест 8882 м. Глибина Маріанської западини у Тихому океані – 10863 м. На скільки метрів перша точка на поверхні земної кулі вища за другу?

 

6. У Липні 1983 р. в Антарктиді була відмічена найнижча на земній кулі температура -89,2, а у вересні 1992 в м. Тріполі (Північна Америка) була відмічена найвища температура +58. Знайдіть різницю між найвищою та найнижчою температурами, відміченими на земній кулі. 

 

 

 

 

                § 4. Розкриття дужок

 

Зразок

1. Спростіть вираз: m+3-(m-n+4)

Розв’язання: m+3-(m-n+4)= m+3-m+n-4= (m-m)+n+(3-4)=0+n+(-1)=n-1.

2. Запишіть різницю виразів і спростіть її: а+15,4 і 7,9-а

 

Розв’язання: (а+15,4)-(7,9-а)=а+15,4-7,9+а=(а+а)+(15,4-7,9)=2а+7,5

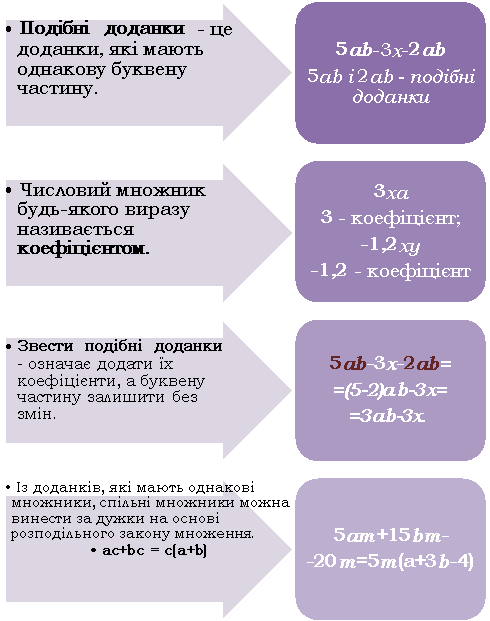
Подібні доданки.

          Зведення подібних доданків

Зразок

1. Зведіть подібні доданки

4а-18а+7а=(4-18+7)а=7а

 

2. Спростіть вирази

 

Спочатку необхідно розкрити дужки, а потім – звести подібні доданки.

а) -(х+9)-5(-2х+7ху)= - х – 9 -5*(-2х)-

-5*7ху= - х – 9+10х-35ху=9х-9-35ху

 

У виразі може бути кілька груп подібних доданків. При спрощенні таких виразів потрібно спочатку виділити групи подібних доданків, а потім у кожній групі звести подібні.

 

б) 6а-7b+12-5a-3b= (6a-5a)+(-7b-3b)+12= a-      - 10b+12.

3. Винесіть за дужки спільний множник

 

Для цього слід застосувати розподільну властивість множення, записавши спочатку добуток кожного із доданків.

3ma-6mb-9mc= 3ma-2mb-33mc=3m(а-    -2b-3с).

 

 

Тренувальні вправи

 

1. Знайдіть вираз, який дістанемо, розкривши дужки у виразі:

-m-(n-p)

1. -m-n-p;    б) -m-n+p;   в) m+n+p;  
2.  г) m-n+p.

 

2. Який з наведених виразів дорівнює сумі виразів: (2у-3); (-3); (3-5у)?

а) 3у-3; б) -3у-3; в) 5у-6; г) 3у-3+6.

 

3. Знайдіть значення виразу: 3(5а+2b), якщо а=3,5; b=-8,2.

 

    4.  Спростіть вирази:

 -1,8x;                        -9a-9b+a+12b;

   -3(c-5)+6(c+3).

 

    5. Знайдіть вираз, який дістанемо, розкривши дужки у виразі: 2k(3a-5b-2c)

 a) 6ak -10bk – 4ck;          б) 6ak + 10bk+4ck;

         в) -6ak +10bk+4kc;         г) -3ak-5bk-4kc.

 

   6.  Який вираз дістанемо, винісши за дужки спільний множник? 5px-10py+15pk

       a) 5p(x+2y-3k);               б) -5p(-x+2y-3k);

                     в) p(-5x+10y-15k).

                    §5. Множення раціональних чисел

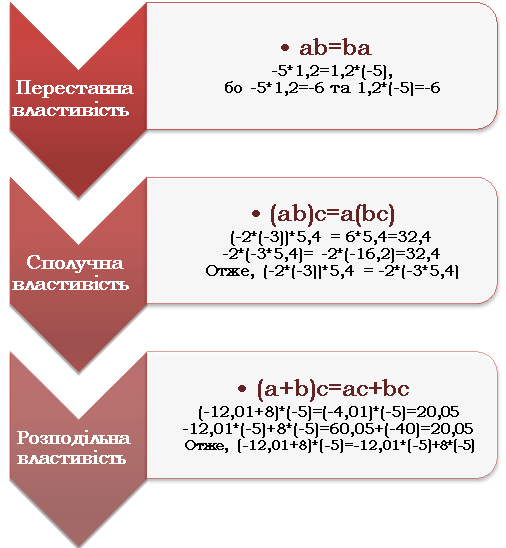Правила множення

Для того, щоб перемножити два числа з однаковими знаками, треба помножити модулі цих чисел і поставити перед отриманим добутком знак «+»	(+17)(+5)=175=175=75   (-17)(-5)=-17-5=175=75
Добутком двох від’ємних чисел є число додатне	-28(-3)=84
Для того, щоб перемножити два числа з різними знаками, треба помножити модулі цих чисел і поставити перед отриманим добутком знак «-»	(-1,5)0,2=-(-1,50,2)= -(1,50,2) = -0,3   1,4(-3) =  -(1,43) = -4,2
При зміні знаку будь-якого множника знак добутку змінюється	1,20,3 =0,36 -1,20,3 =-0,36 1,2(-0,3) =-0,36

 

 

 

 

              §6. Властивості множення

 

 

 

Завдання для самоперевірки

«Продовжіть речення»

 

1. Для того, щоб перемножити два числа з однаковими знаками, треба…
2. Добутком двох від’ємних чисел є число…
3. Для того, щоб перемножити два числа з різними знаками, треба…
4. Добуток дорівнює одному з множників, якщо…
5. Щоб перевірити переставну властивість множення, потрібно…
6. Щоб перевірити сполучну властивість множення, потрібно…
7. Наведіть приклади застосування  розподільної властивості множення.

Знайдіть помилку у міркуваннях:

Доведемо, що 5=6. Для цього запишемо правильну рівність: 35+10-45=42+12-54. Винесемо за дужки спільні множники лівої і правої частини цієї рівності. Дістанемо: 5(7+2-9)=6(7+2-9). Розділимо обидві частини цієї  рівності на спільний множник (той, що в дужках) і дістанемо: 5=6.

Тренувальні вправи

 

1. Виконайте  множення

(-125)                            84(-25);

(-72)                      (-64)

2. Виконайте дії

(-12+5)(3-(-7));      (-63 – (+28) – (-84))(-5);

(-11)(-19) – (-12) – (-7)).

3. Виконайте множення

(-117)(-877)(-914)0;     121(-242)(-363);

(-0,1)(-0,2)(-0,5);           (-3,73)105,12(-1).

4. Знайдіть значення виразу

(-3)(-7)5+3(-5)7;          (-15,3 – 24,3

(-)

5. Спростіть вираз

х(-2,1)(-1)0,3;                 -1,8 (-2)(+0,5)b;

(+1)(-1)с(-1,7);          ()(-)(-)(-24). 

6. Обчисліть добуток, застосувавши закони множення

-21(-290)+190(-21);  - ;

-11370+(-11)230;     

 

 

           §7. Ділення раціональних чисел

 

 

 

Частка двох чисел з однаковими знаками – число додатне	125:5=25 (-125):(-5)=25
Частка двох чисел з різними знаками – число від’ємне	125:(-5)=-25 (-125):5=-25
Для того, щоб знайти модуль частки, треба модуль діленого розділити на модуль дільника	-7,5:1,5=--7,5:1,5= =-(7,5:1,5)=-5
При діленні нуля на будь-яке число, яке не дорівнює нулю, отримують нуль. На нуль ділити не можна!	0:(-1,178)=0 0:
При діленні числа на 1 отримуємо частку, яка дорівнює діленому. а:1=а	-117,21:1 = -117,21
При діленні числа на (-1) отримуємо частку, протилежну діленому. а:(-1)= - а	-117,21:(-1) = 117,21

 

Зразок

1. Обчисліть:(.

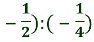Розв’язання:

Застосуємо правило ділення чисел з однаковими знаками.

(=

 

2. Виконайте дії (5,44 + (-0,16):(-0,4))-(-1,48-       -1,12):(-1,5)

 

Розв’язання: Зручно виконувати розв’язання таких прикладів за діями, враховуючи порядок дій. В першу чергу виконують дії в дужках, множення та ділення, а потім додавання та віднімання.

1. (-0,16):(-0,4)=0,4
2. 5,44+0,4=5,84
3. -148 – 1,12= - 2,5
4. 5,84 – (-2,5)= 5,84 + 2,5 = 8,34
5. 8,34:(-1,5) = -(83,4:15)= - 5,56.

 

Відповідь: -5,56

 

 

 

 

Тренувальні вправи

1. Знайдіть частку

-69:23;                                       39:(-13);

-72:(-12);                                   -96:(-16);

-6,72:3,2;                                   13,44: (-5,6).

     2. Знайдіть частку

 5,88:(-2,8);                                 -22,8:(-0,38);

 -5,32:(-0,14);                             -14,4:1,2;

 10,88: (-36);                               -5,7:19.

     3.Обчисліть 

 -2: (-);                                  -7

 -                          ;

                                2

 3                            (-):(-

     4.Виконайте дії 

 0,5:3       -

         -1    -7

  -3):0,2. 

      5.Вставте у порожні клітинки числа так, щоб дії було виконано правильно: 

 108 :         = -18 : 0,25;

 -8: (-0,2) = 0,5  

 -0,72 

 

Запитання для самоперевірки

«Де помилка?»

Знайдіть помилку у твердженнях, сформулюйте правила вірно, обґрунтуйте свою думку.

2. Частка двох чисел з однаковими знаками – число від’ємне.
3. Для того, щоб знайти модуль частки, треба модуль дільника розділити на модуль діленого.
4. Частка двох чисел з різними знаками – число додатне.
5. Ділити нуль на будь-яке число не можна.
6. При діленні будь-якого числа на нуль отримують нуль.
7. При діленні числа на 1 отримуємо частку, яка дорівнює числу протилежному діленому.
8. При діленні числа на (-1) отримуємо частку, яка дорівнює діленому.

 

 

 

Анкета - рецензія за результатами апробації

міні-підручника математики „Раціональні числа та дії над ними. 6 клас”

1. Чи відповідає міні-підручник програмі з математики?
   1. Так, міні-підручник „Раціональні числа та дії над ними. 6 клас”, створений відповідно до програми з математики.
   2. Ні, матеріал зібраний в міні-підручнику довільно, програмним вимогам не відповідає.
2. Яку форму має міні-підручник?
   1. Він має тільки приклади для розв’язання за темою «Раціональні числа та дії над ними»
   2. Він має форму збірки узагальненого теоретичного та практичного матеріалу з теми «Раціональні числа та дії над ними», що вивчається в курсі 6 класу.
3. Яке практичне застосування міні-підручника ви бачите?
   1. Міні-підручник є гарна підказка на контрольній роботі.
   2. Наведені приклади дають змогу навіть дітям із початковим рівнем навчальних досягнень привчають до системності при повторені та підготовці до контрольної роботи.
4. Як побудовано зміст міні-підручника?
   1. Підручник має чітку структуру, кольорове і шрифтове виділення опорних слів, висновків.
   2. Структура міні-підручника змішана, дуже важко зрозуміти за яким принципом зібрано та розподілено матеріал.
5.               Яке значення цього підручника для учнів 6-х класів?
   1. Такий підручник не є обов’язковим для учнів 6-х класів. Готуючись до контрольної роботи учні можуть і самостійно вибрати необхідний матеріал з підручника.
   2. Він має важливе практичне значення не лише на узагальненому уроці завдяки своїй структурі, унікально підібраному матеріалу.
6. Чи знадобиться міні-підручник вам після вивчення теми?
   1. Зміст міні-підручника надає можливість одночасно повторити весь навчальний матеріал з теми та використовувати його як довідник при подальшому вивченні курсу математики.
   2. Міні-підручник дуже цікавий при підготовці до контрольної роботи за темою, але подальшого практичного значення він не має. В ньому зібрана тільки одна тема, тому при вивченні інших тем він більше не знадобиться.

Висновок: («так» чи «ні»)

Пропонуємо використовувати міні-підручник всім учням 6-х класів при опрацювання теми «Раціональні числа та дії над ними» та як довідник при подальшому вивченні математики, бо тема «Раціональні числа та дії над ними» є однією з головних тем курсу 6-го класу.

Рецензію склали              __________________________________                           

                      

 

Зміст

§ 1. Додавання раціональних чисел                3

§ 2. Властивості додавання    4

§3. Віднімання раціональних чисел  7

§ 4. Розкриття дужок. Подібні доданки.

          Зведення подібних доданків    11-12

§5. Множення раціональних чисел               15

§6. Властивості множення               16

§7. Ділення раціональних чисел         19