Розв’язування задач прикладного характеру           з застосуванням похідної.

 

 

 

 

 

 

 

 

 

Операція знаходження похідної називається  диференціюванням.

Значення похідної в точці x₀ дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою x₀ і дорівнює кутовому коефіцієнту цієї дотичної. У цьому полягає геометричний зміст похідної.

Рівняння    дотичної   до   кривої         у = f(x) в

 

точці М(x_o; у_o) має вигляд: y – y_о = f ‘(x_o)(x – x_o).

Геометричний     зміст похідної використовують

під час дослідження функцій

 

Застосування похідної         для      дослідження                 функцій

Якщо     y'(x)     >     0,     то     функція     зростає.

Якщо       y'(x)     <     0,     то     функція     спадає.

Якщо y'(x) = 0 (або не існує), то в точці x =

 

x₀ знаходяться критичні точки функції (серед яких можливі точки максимуму або мінімуму).

Використання похідної в інших галузях

 

Похідну в хімії використовують для визначення швидкості хімічних реакцій. У біології - для визначення приросту популяції виду.

В економічних науках похідна допомагає  визначити еластичність попиту, крім того похідна від обсягу виробленої продукції по  

часу визначає продуктивність

 

 

 

 

 

Поняття похідної виникло у ХVІІ ст. у зв’язку з необхідністю розв’язати деякі математичні і фізичні задачі. Задачу про побудову дотичної розв’язав Г.Лейбніц, про визначення миттєвої швидкості під час прямолінійного нерівномірного рухуІ.Ньютон, який прийшов до поняття похідної, виходячи з положень механіки. Результати  своїх досліджень І.Ньютон виклав у трактаті „Метод флюксій”, опублікованому в 1736 році. Учений називав похідну флюксією, а саму функцію – флюентою.

•  Похідна – це швидкість зміни функції. Нехай матеріальна точка рухається вздовж координатної прямої х за законом х=х(t). Тоді похідна від координати за часом у даний момент є швидкістю руху в цей момент часу. У цьому й полягає її механічний зміст.

•  Поняття похідної як швидкості зміни функції використовується під час означень багатьох фізичних величин. Наприклад, похідна швидкості руху за часом є прискорення; похідна величини заряду за часом є сила струму; похідна потоку магнітної індукції за часом є електрорушійна сила індукції; похідна роботи за часом є потужність

 

 

Розвяжіть усно завдання 1-4, користуючись графіком функції 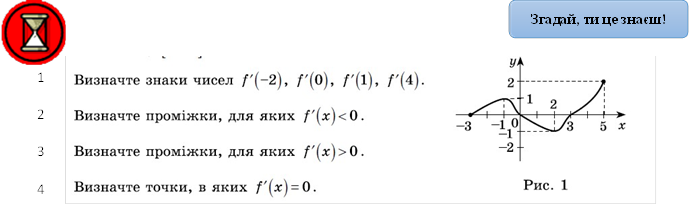y=f(x)на проміжку [-3;5] ( рис.1).

 

Розвяжіть усно завдання 5-6, користуючись тим, що закон зміни координати х матеріальної точки від часу t під час прямолінійного руху вздовж осі Ох задається функцією  x(t)=t³-2t²+4t-3

5

6

 

Виконайте усно тестові завдання 7-8, обравши одну правильну відповідь

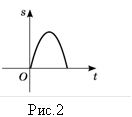
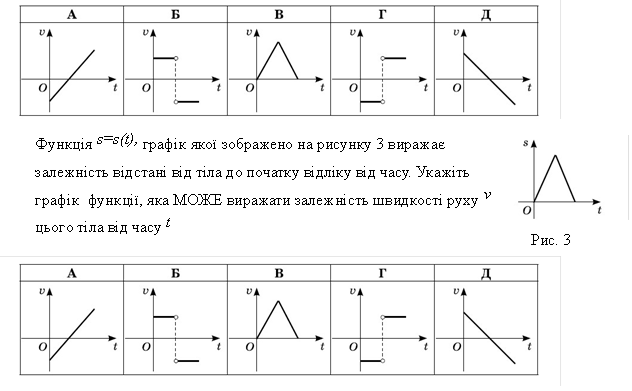
7  Функція s=s(t), графік якої зображено на рисунку 2 виражає

залежність відстані від тіла до початку відліку від часу. Укажіть графік  функції, яка МОЖЕ виражати залежність швидкості руху v цього тіла від часу t

8  9     Укажіть геометричні перетворення графіка функції y=f(x), визначеної на проміжку(- ∞; +∞). які слід виконати, щоби

отримати графіки функцій y=g(x), наведених у завданнях 1-8. Укажіть координати точки М’, у яку переходить точка М (6;-2), що належить графіку функції  y=f(x). внаслідок цих перетворень. Заповніть відповідну таблицю.

№	Геометричні перетворення	Координати М’(х;у)		№	Геометричні перетворення	Координати М’(х;у)
1	g(x)=f(x)+2			5	g(x)= f(3x)
2	g(x)=f(x-4)			6	g(x)=f ( x )
3	g(x)=-f(x)			7	g(x)=2f(x)
4	g(x)= f(x)			8	g(x)=| f(x)|

 

             Кількість правильних відповідей ______________                        Перевірив_____________________

зі швидкістю х  км/год. Пасажир, сідаючи в таксі, може обирати швидкість руху автомобіля. Яку швидкість (у км/год) має обрати пасажир, щоб його витрати на 1км шляху були

НАЙМЕНШИМИ?

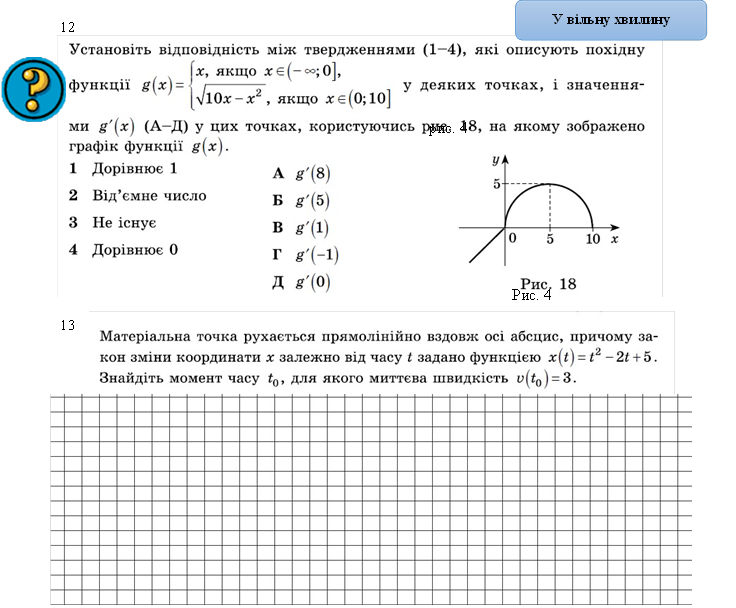
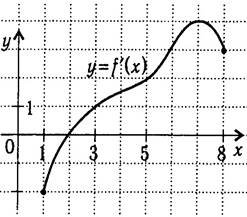
14 Функція визначена на проміжку [х1;х2]. На рисунку зображено графік похідної у= f ^׳(х). По графіку похідної визначте, яку абсцису має точка на графіку функції  у= f ^׳(х), дотична якої має кутовий коефіцієнт, що дорівнює 2

 

 

2

2.   За якого значення параметра с найменше значення функції y= x⁴ – 8x² +c на відрізку  [-1;3]дорівнює 30

3.   При якому найбільшому значенні параметра а функція f^׳(х)= -х³+(а+6)х+5 спадає на всій числовій прямій

4.   Задано функцію f^׳(х)= 3х⁴-4х³-12х²

1.  Знайдіть проміжки зростання та спадання функції, екстремуми функції.

2.  Побудуйте ескіз графіка функції у= f^׳(х).

3.  Знайдіть кількість коренів рівняння f^׳(х)=а, де а∈ 𝑅𝑅, залежно від значень параметра а

                                                                         Додаток № 1(учнівський проект)                       

Шановні учні!

Уявіть собі 2200 рік. Група учнів 143 гімназії міста Києва відправилася в

наукову експедицію на міжзоряному кораблі до нещодавно відкритої планети. Корабель на підльоті до зоряної системи помітно зменшив швидкість, “повільно” наближався до третьої планети цієї системи. На екрані, збільшуючись у розмірах, “висіла” куля з чіткими обрисами материків, гірських хребтів, рік…За допомогою комп'ютера допитливий учень Вася Пупкін визначив радіус планети. Він виявився рівним 6000 км. Попередньо захопивши в бібліотеці школи фізичний довідник, Вася швидко знайшов значення гравітаційної постійної: G = 6,67.10^–11 Н·м²/кг². Для визначення маси цієї планети йому необхідно було  попрацювати з комп'ютером... І в цей момент роздався голос капітана корабля: “Увага! Ми знаходимося на висоті 100 км над поверхнею. Наша швидкість 30 км/с. Починаємо екстрене гальмування”. “Нічого, — подумав Вася. — захоплю з собою лінійку, секундомір, нитку і маленький вантаж. Виміряю на поверхні планети  прискорення вільного падіння і знайду її масу”.

              Через 30 хвилин група перших дослідників вийшла з космічного корабля. Серед них був і Вася. Він швидко зробив виміри і визначив спочатку прискорення вільного падіння, а потім і масу планети. Як, по-вашому, він це зробив?

Домашнє завдання:

За даним  текстом спробуйте сформулювати свої цікаві задачі. Тексти задач підготуйте до наступного уроку. Успіхів вам!

Додаток № 2  (тестування)

 

1.     За 6 с маятник зробив 12 коливань. Чому дорівнює частота коливань?

                               А. 0,5 Гц         Б. 2 Гц          В. 72 Гц         Г. 6 Гц

 

2.     Як зміниться період коливань вантажу на пружині, якщо масу вантажу зменшити в 4 рази?

                    А.  Збільшиться в 4 рази                      Б.  Збільшиться в 2 рази

                    В.  Зменшиться в 2 рази                     Г.  Зменшиться в 4 рази

 

3.     Як зміниться період коливань вантажу на пружині, якщо жорсткість пружини зменшити в 16 разів?

                    А.  Збільшиться в 4 рази                      Б.  Збільшиться в 16 разів

                    В.  Зменшиться в 16 разів                     Г.  Зменшиться в 4 рази

 

4.     Координата тіла, яке коливається змінюється за законом х = sin ( πt ). Чому дорівнює період коливань? Усі величини виражені в одиницях СІ.

А.¼  с         Б. ½  с          В. 2 с        Г. 4 с

 

5.     Яким виразом визначається частота коливань математичного маятника?

                                                           А. 2_π         Б. 2_π          В.               ¹                Г.        ¹      

                                                                                                                                   2_π l / g                   2_π g /l

6.     Який приблизно період коливань математичного маятника довжиною 90 м? Прийняти прискорення вільного падіння g = 10 м/с².

А.1/18 з         Б. 1/3 с.          В. 3 с.         Г. 18 с.

 

7.     Як зміниться період коливань математичного маятника, якщо його довжину збільшили в 9 разів?

                    А.  Збільшиться в 3 рази                      Б.  Збільшиться в 9 рази

                    В.  Зменшиться в 3 рази                     Г.  Зменшиться в 9 рази

 

8.     Яке з перерахованих коливань є вільним? а) Коливання вантажу на пружині, після однократного його відхилення від положення рівноваги; б) Коливання дифузора гучномовця під час роботи приймача.

А.Тільки а)         Б.  а) і б)          У. Тільки б)         Г. Ні а),  ні б)

 

9.     Вантаж підвішений на нитці і відхилений від положення рівноваги так, що його висота над землею збільшилася на 20 см. Приблизно з якою швидкістю тіло буде проходити положення рівноваги при вільних коливаннях?

                               А. 1 м/с         Б. 2 м/с          В. 4 м/с         Г. 20 м/с.

 

10. При вільних коливаннях вантажу на пружині максимальне значення його потенціальної енергії 10 Дж, максимальне значення кінетичної енергії 10 Дж. У яких межах змінюється повна механічна енергія вантажу і пружини?

                А.  Змінюється від 0 до 10 Дж                Б.  Змінюється від 0 до 20 Дж

                В.  Не змінюється і дорівнює 10 Дж      Г.  Не змінюється і дорівнює 20 Дж

 

 

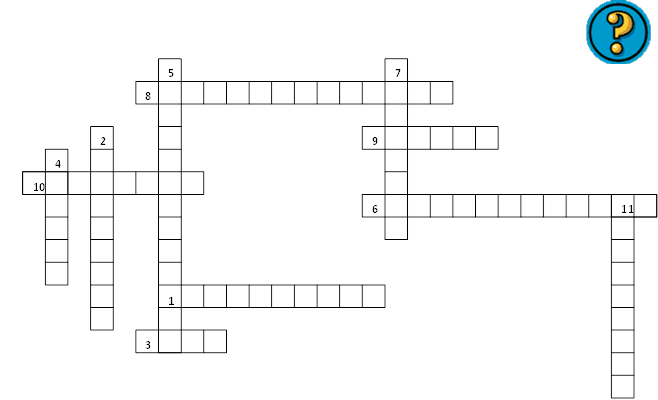Додаток № 3 (кросворд)

 

 

ЗАПИТАННЯ ДО КРОСВОРДА:

 

1.                   Одна із величин, значення  якої повторюється при коливальному русі.

2.                   Коливання, які відбуваються  у замкненій системі.

3.                   Одиниця вимірювання частоти коливань.

4.                   Величина, обернена частоті коливань.

5.                   Коливання, які відбуваються  за законом синуса або косинуса.

6.                   Яка з енергій максимальна при найбільшому відхиленні маятника від положення рівноваги?

7.                   Яка із кінематичних величин максимальна при проходженні тілом положення рівноваги?

8.                   Маятник, період коливань якого залежить від довжини нитки.

9.                   Одна із причин затухання вільних коливань.

10.               Явище, яке виникає при співпаданні власної частоти коливань та частоти зовнішньої вимушуючої сили. 

11.               Величина, яка зростає при співпаданні власної частоти коливань з частотою коливань зовнішньої вимушуючої сили. 

 

1. 

 

 

 

 

 

 

2. 

 

 

 

 

3