Многогранники. Призми і паралелепіпеди
Проведення навчальних лекцій в умовах компетентнісно орієнтованої системи математичної підготовки старшокласників потребує особливо ретельної підготовки вчителя, по-перше, з боку привернення уваги до способу фіксування матеріалу учнями. З метою навчання учнів конспектування навчального матеріалу, на наш погляд, є методично виправданим у 10-11-х класах використовувати опорні конспекти, які друкуються на окремих аркушах, для того, щоб навчити учнів виділяти головне, правильно записувати означення, акуратно (від руки) виконувати креслення тощо. З іншого боку, для підсилення ролі унаочнення, активізації учнівської уваги та кращого засвоєння ними пропонованих знань, є доцільним використання на занятті сучасних інформаційно-комунікаційних технологій та засобів мультимедіа, зокрема – мультімедійного проектора (мультимедійної, інтерактивної дошки), педагогічних програмних засобів, рекомендованих Міністерством освіти та науки України. Це дозволить демонструвати потрібні рисунки, таблиці, проектувати на екран окремі завдання й побудови.
1
«Многогранники. Призми і паралелепіпеди».
Цілі уроку
Розвивальна: сприяти розвитку просторового мислення, оперування просторовими категоріями й поняттями; вмінь фіксувати та свідомо використовувати навчальну інформацію (загальні навчальні компетенції).
Дидактична: формування знань основних понять теми, навичок розпізнавання та зображення просторових тіл (призм і паралелепіпедів) на площині; вмінь застосовувати властивості виучуваних понять на практиці, при розв’язуванні типових задач (предметні компетенції).
Виховна: сприяти вихованню цілеспрямованості, наполегливості у виконанні освітніх завдань, культури математичної мови та мислення, графічної культури, інтерес до вивчення математики (особистісні компетенції).
Обладнання: мультімедійний проектор (мультимедійна дошка), педагогічний програмний засіб – пакет динамічної геометрії DG або GRAN 3D, аркуші для складання опорного конспекту (на друкованій основі).
Лекція розрахована на одну академічну годину. Комп’ютерна підтримка викладу навчального матеріалу передбачена шляхом показу слайдів (презентації Power Point) і демонстрації побудов зображень фігур у динаміці. В наведеному нижче опорному конспекті записі, які мають бути виконані учнями, подані курсивом.
Опорний конспект лекції
Тема: Многогранники. Площі поверхонь і перерізи многогранників. Призми і паралелепіпеди
- Многогранники та їх елементи. Перерізи многогранників
Геометричне тіло – об’єднання скінченої просторової області і її поверхні.
Многогранник – тіло, поверхня якого складається із скінченої кількості многокутників.
![]()
![]()
![]() Грані многогранника - многокутники, які обмежують многогранник
Грані многогранника - многокутники, які обмежують многогранник![]()
Діагональ многогранника – відрізок, який сполучає дві вершини, які не належать одній грані.
Опуклий многогранник розміщений з одного боку від площини кожної його грані.
Усі грані опуклого многогранника – опуклі многокутники.
|
|
опуклий семигранник
|
|
семигранник неопуклий |
Розгортка многогранника
 Одержання розгортки: поверхню многогранника розрізати по ребрах і розпластати на площині
Одержання розгортки: поверхню многогранника розрізати по ребрах і розпластати на площині
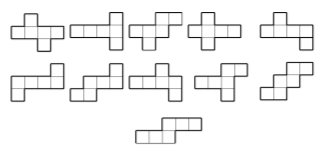
Розгортки куба
Площа поверхні многогранника – це сума площ усіх його граней, вона дорівнює площі розгортки даного многогранника.
Січна площина: якщо принаймні дві точки многогранника лежать по різні боки від площини, ця площина перетинає многогранник, її називають січною площиною.
Переріз многогранника – фігура, яка складається з усіх точок, спільних для многогранника та січної площини.
Кожний переріз опуклого многогранника – опуклий многокутник.
![]()
![]()
![]()
![]()

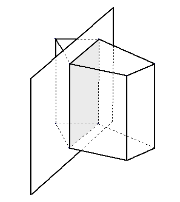
- Види многогранників.
Призми і паралелепіпеди
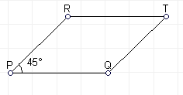
Призма – многогранник, у якого дві грані – рівні п-кутники, а решта граней – паралелограми.


![]()
![]() Призми
Призми
![]()
![]()
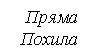
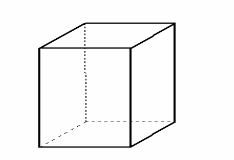
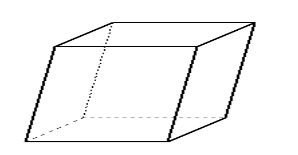



|
|
Січна площина, паралельна основі, перетинає її по многокутнику, що дорівнює основі. |
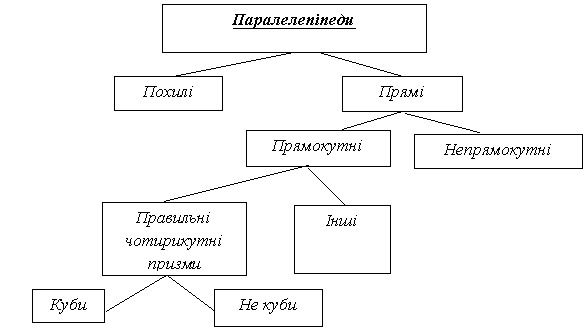
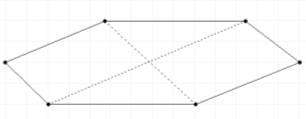
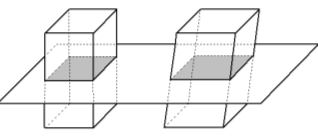
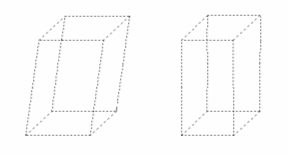
Паралелепіпед - призма, основа якої паралелограм.
Прямий паралелепіпед – такий, бічні ребра якого перпендикулярні основі.
Прямокутний паралелепіпед – той, в якого всі грані – прямокутники.
Довжини трьох ребер прямокутного паралелепіпеда називають вимірами цього прямокутного паралелепіпеда.
Куб – прямокутний паралелепіпед, усі три виміри якого рівні.
- Теореми про властивості паралелепіпедів
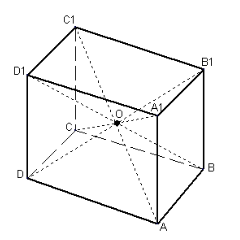
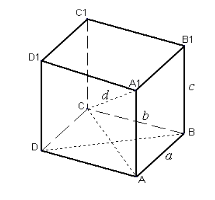
Теорема 1: діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою пополам.
Доведення:
|
Нехай діагоналі АВC1D1 і CDA1B1 перетинаються в точках О і О1, які є серединами відрізків АC1 і DB1. АC1 і DB1 – діагоналі паралелограма АDC1B1, звідси точки О і О1 – збігаються. Таким чином, середина кожної діагоналі паралелепіпеда – одна й та сама точка О, що й треба було довести. |
Властивість точки перетину діагоналей паралелепіпеда:
ця точка є центром симетрії паралелепіпеда.
Теорема 2: квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів:
d2 = a2 + b2 + c2
Теорему 2 довести самостійно, скориставшись рисунком на аркуші 5.
|
|
Дано: Довести: Доведення: |
Приклад задачі: розміри цеглини 250×120×65 мм. Знайдіть відстань між її найвіддаленішими точками.
Розв’язання
Цеглина має форму прямокутного паралелепіпеда. Найвіддаленіші її точки – кінці діагоналі паралелепіпеда, тому шукана відстань
![]()
Відповідь: 285 мм.
- Обчислення площ поверхонь призм і паралелепіпедів
|
Вид многогранника |
Sбічн |
Sповн |
|
Призма похила Паралелепіпед |
Сума площ бічних граней |
Sп = Sб + 2 So, де Sб – площа бічної поверхні, So – площа основи
|
|
Призма пряма Прямокутний пар-д |
Sб = Рh, де Р – периметр основи h – висота прямої призми (прямокутного паралелепіпеда) |
|
|
куб |
Sб = 4а2, де а – ребро куба |
Sп = 8а2, де а – ребро куба |
- Зображення на площині призм і паралелепіпедів
Вимоги до зображення: правильність, наочність, зручність (простота) виконання.
Зображення многокутників на площині
Правильний трикутник
|
1 спосіб |
2 спосіб |
Прямокутник, квадрат
|
|
|
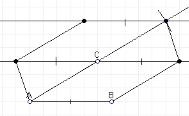
Правильний шестикутник
|
Через рівні трикутники |
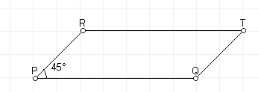
Через паралелограм |
Запитання для самоперевірки
- Сформулюйте означення геометричного тіла.
- Сформулюйте означення многогранника, його граней та діагоналей.
- Як отримати розгортку многогранника?
- Які ви знаєте многогранники, дайте їх означення.
- Як знайти площі поверхонь призм і паралелепіпеда.
- Які властивості паралелепіпедів ви знаєте?
- Доведіть теореми 1-2.
- Як побудувати просторове зображення паралелепіпеда, основами якого є правильний трикутник, прямокутник, правильний шестикутник?
Матеріал лекції (і опорного конспекту) підготовлений за підручником. Усі рисунки, таблиці, схеми, а також відтворення розв’язування задач і доведення теорем (окрім тих, доведення яких учням пропонується розглянути самостійно за підручником) висвітлюються на екрані за допомогою мультімедійного проектора. При демонстрації побудов та зображень використовується педагогічний програмний засіб DG (послуга покрокового відтворення побудов). Який це має вигляд, розглянемо на прикладі відтворення повної побудови зображення проекції на площині правильного шестикутника:
 Перший і другий кроки
Перший і другий кроки 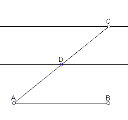
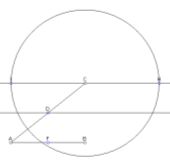 3-ій-5-ий кроки
3-ій-5-ий кроки 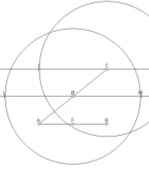



про публікацію авторської розробки
Додати розробку