Многогранники. Розв язування вправ. Відкритий урок
Відкритий урок 11 клас геометрія
Тема: «Многогранники. Розв’язування вправ і задач».
Мета: - закріпити знання про многогранники, їх елементи, площі бічної і повної поверхонь;
- розв’язувати задачі на знаходження елементів, площ поверхонь тіл;
Ключові компетентності:
- Спілкування державною мовою: ставити запитання і розпізнавати проблему; розвивати логічне мислення; робити висновки на основі інформації; аргументувати, доводити правильність тверджень;
- Математична: оперувати геометричними об’ єктами на площині і в просторі; усвідомлення важливості математики, як універсальної мови науки;
- Інформаційно-цифрова: уміння діяти за алгоритмом; знаходити інформацію та оцінювати її достовірність.
Хід уроку
І. Організаційний момент. Мотивація навчальної діяльності.
Видатний французький архітектор Ле Корбюзі сказав: «Ми живемо в геометричний період. Усе навколо – геометрія».
І справді, світ, в якому ми живемо, наповнений геометрією будинків і вулиць, творіннями природи і людини, в яких можна знайти геометричні елементи.
Геометрія є могутнім інструментом пізнання природи і створення техніки. Вона виявляється скрізь, де потрібна найбільша точність у визначенні форми і розмірів : техніку, інженеру, архітектору, робітнику - всім необхідна геометрична уява.
- Тема нашого уроку: «Розв’язування задач на обчислення площ поверхонь многогранників».
- Сьогодні ми закріплюємо знання про многогранники, їх елементи, площі їх поверхонь.
ІІ. Перевірка засвоєння теоретичного матеріалу.
- Як сказав французький філософ , письменник, фізик, математик Блез Паскаль: «Цінними є не ті знання, які відкладаються в голові, як жир, а ті, які перетворюються в мисленнєві м язи».
- Зараз ми з вами і потренуємо ці мисленнєві м язи: проведемо математичний диктант.
1. Математичний диктант
Я читаю твердження, вам треба визначити: правильне воно чи хибне. У вас є ланцюжок пронумерованих квадратиків. Це номера запитань. Якщо твердження правильне, ви креслите дугу над номером питання, якщо хибне, то дугу креслите під ним.
( Перед уроком усім учням були видані листки для відповідей, картки самооцінювання)
Увага! Починаємо:
1) Бічні грані прямої призми є прямокутниками (Правильно).
2) Чи правильне твердження, що у трикутної призми 9 ребер? (Правильне)
3) Чи правильним є твердження, що в основі призми, у якої 15 ребер, лежить п ятикутник? (Правильне)
- Площа прямокутного трикутника дорівнює: ав/3 , де а,в-катети. (Неправильне/ ав/2)
-
Площа повної поверхні куба дорівнює 4
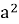 , де а – сторона куба. (Неправильне/ 6
, де а – сторона куба. (Неправильне/ 6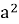 ,)
,)
- У правильній піраміді усі бічні ребра рівні (Правильне)
- Апофема - це висота піраміди (Неправильне /це висота бічної грані)
- У чотирикутної піраміди 8 ребер (Правильне).
Ключ-відповідь:
|
1
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Оцінювання: кожне завдання по 0,5 балів.
2. Актуалізація знань. Перегляд презентації «Многогранники»
3. Розв’язування усних вправ. Вправа «Знайди помилку»
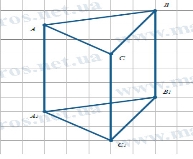
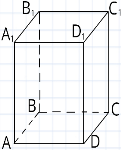
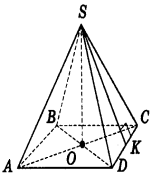
- 2) 3)
АА = 5 см
ВВ = 6 см АС – діагональ SK – висота піраміди
СС = 6 см призми
Під час обгрунтування відповідей, учні дають означення елементів геометричних тіл та їх властивостей.
4. Перевірка засвоєння формул.
« У математиків існує своя мова - формул».
С.В. Ковалевська
Вислів записано на дошці (плакат формату А3).
То ми з вами зараз і «поговоримо» цією мовою - мовою формул.
Завдання на відповідність.
Завдання: Вибрати формули, які відповідають геометричним тілам .



1) 2) 3)
Картки з формулами:
А) S бічн. пов = 2(AB + BC)![]()
![]() ;
;
Б) S повн. пов. = S бічн. пов. + 2 ![]() ;
;
В) S повн. пов. = S бічн. пов.+2( AB![]() BC);
BC);
Г) S бічн. пов = ½ Р осн ![]() SK;
SK;
Д) S повн. пов. = S бічн. пов. + ( AB![]() BC);
BC);
Е) S осн = ![]()
![]() / 4;
/ 4;
Ж) S бічн. пов = 3AB ![]()
![]() ;
;
ІІІ. Перевірка практичних навичок.
Усна робота
 АВ=3; ВС = 5 ;
АВ=3; ВС = 5 ; ![]() = 8. Знайти S бічної поверхні
= 8. Знайти S бічної поверхні
2)
 АВ= ВС = 4 ;
АВ= ВС = 4 ; ![]() = 5. Знайти S бічної поверхні
= 5. Знайти S бічної поверхні
3)
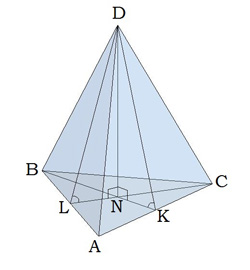 АВ= 8; АС = 6 ; DK = 9.
АВ= 8; АС = 6 ; DK = 9. ![]() АВС = 90
АВС = 90![]()
Знайти S бічної поверхні
![]() Письмова робота 1
Письмова робота 1
Декілька учнів працюють за партами самостійно за індивідуальними завданнями (картками) , а інші учні класу в цей час працюють ( колективно) над розв’язуванням задачі, умова якої записана на листку формату А 3 і вивішена на дошці.
Задача ( колективне рішення)
Площа бічної поверхні правильної трикутної призми, всі бічні грані якої є квадрати, дорівнює 12 ![]() . Знайдіть кут між площиною основи та перерізом призми ( площиною, проведеною через ребро основи ВС і середину протилежного бічного ребра).
. Знайдіть кут між площиною основи та перерізом призми ( площиною, проведеною через ребро основи ВС і середину протилежного бічного ребра).
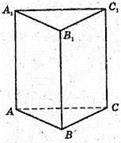
( Після обговорення розв’язування задачі записується на дошці).
Письмова робота 2.
Самостійна робота. Розв’язування задач. ( 10 хв)
1 варіант.
- Скільки вершин, ребер, граней має семикутна призма?
- Знайти площу бічної поверхні і площу повної поверхні правильної чотирикутної піраміди, в якої сторона основи дорівнює 5 см, а апофема дорівнює 8 см.
2варіант.
- Скільки вершин, ребер, граней має вісьмикутна піраміда?
-
Знайти площу діагонального перерізу правильної чотирикутної призми, в якої площа основи дорівнює 144
 , а бічне ребро дорівнює 10 см.
, а бічне ребро дорівнює 10 см.
Картки із задачами.
Картка 1.
Знайти площу розгортки многогранника, у якого одна грань – квадрат зі стороною а, а решта четверо граней - правильні трикутники.
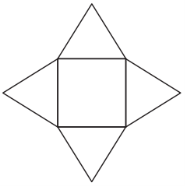
Картка 2.
Знайти площу поверхні правильної трикутної призми, сторона основи якої дорівнює 3 см, а бічне ребро дорівнює 5 см.
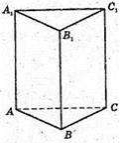
Картка 3.
Площа бічної поверхні правильної чотирикутної піраміди дорівнює S. Знайдіть площу основи піраміди, якщо її апофема дорівнює l .

V. Підсумок уроку
(Самооцінювання учнів )
- Дякую всім за урок. Урок закінчено.
Д/з. Скласти кросворди із ключовими словами : призма, піраміда.
Картка самооцінювання
Прізвище, ім’ я________________________________________________
Клас __________________
|
№ |
Завдання |
Максимальна кількість балів |
Само-оцінювання, балів |
|
1 2 3 4 5 |
Математичний диктант Вправа «Знайди помилку» Використання формул Задачі за готовими малюнками Колективне розв’ язування задачі Всього балів: |
2 2 2 2 2
10 |
|
Ключ-відповідь
|
1
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
11 клас Геометрія
Самостійна робота. Розв язування задач
- варіант
- Скільки вершин, ребер, граней має семикутна призма?
- Знайти площу бічної поверхні і площу повної поверхні правильної чотирикутної піраміди, в якої сторона основи дорівнює 5 см, а апофема дорівнює 8 см.
2варіант
- Скільки вершин, ребер, граней має вісьмикутна піраміда?
-
Знайти площу діагонального перерізу правильної чотирикутної призми, в якої площа основи дорівнює 144
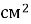 , а бічне ребро дорівнює 10 см.
, а бічне ребро дорівнює 10 см.
______________________________________________________
11 клас Геометрія
Самостійна робота. Розв язування задач
1 варіант
- Скільки вершин, ребер, граней має семикутна призма?
2. Знайти площу бічної поверхні і площу повної поверхні правильної чотирикутної піраміди, в якої сторона основи дорівнює 5 см, а апофема дорівнює 8 см.
2 варіант
1. Скільки вершин, ребер, граней має вісьмикутна піраміда?
2. Знайти площу діагонального перерізу правильної чотирикутної призми, в якої площа основи дорівнює 144 ![]() , а бічне ребро дорівнює 10 см.
, а бічне ребро дорівнює 10 см.
__________________________________________________________
11 клас Геометрія
Самостійна робота. Розв язування задач
1 варіант
- Скільки вершин, ребер, граней має семикутна призма?
- Знайти площу бічної поверхні і площу повної поверхні правильної чотирикутної піраміди, в якої сторона основи дорівнює 5 см, а апофема дорівнює 8 см.
2 варіант
- Скільки вершин, ребер, граней має вісьмикутна піраміда?
-
Знайти площу діагонального перерізу правильної чотирикутної призми, в якої площа основи дорівнює 144
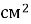 , а бічне ребро дорівнює 10 см.
, а бічне ребро дорівнює 10 см.
Картка самооцінювання
Прізвище, ім я________________________________________________
Клас __________________
|
№ |
Завдання |
Максимальна кількість балів |
Само-оцінювання, балів |
|
1 2 3 4 5 |
Математичний диктант Вправа «Знайди помилку» Використання формул Задачі за готовими малюнками Колективне розв язування задачі Всього балів: |
2 2 2 2 2
10 |
|
Ключ-відповідь
|
1
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
_______________________________________________________________
Картка самооцінювання
Прізвище, ім я________________________________________________
Клас __________________
|
№ |
Завдання |
Максимальна кількість балів |
Само-оцінювання, балів |
|
1 2 3 4 5 |
Математичний диктант Вправа «Знайди помилку» Використання формул Задачі за готовими малюнками Колективне розв язування задачі Всього балів: |
2 2 2 2 2
10 |
|
Ключ-відповідь
|
1
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Картки із задачами.
Картка 1.
Знайти площу розгортки многогранника, у якого одна грань – квадрат зі стороною а, а решта четверо граней - правильні трикутники.
 _____________________________________________
_____________________________________________
Картка 2.
Знайти площу поверхні правильної трикутної призми, сторона основи якої дорівнює 3 см, а бічне ребро дорівнює 5 см.

_____________________________________________________________
Картка 3.
Площа бічної поверхні правильної чотирикутної піраміди дорівнює S. Знайдіть площу основи піраміди, якщо її апофема дорівнює l .

1


про публікацію авторської розробки
Додати розробку
