Множення і ділення десяткових дробів.

Тема. Множення і ділення десяткових дробів.

Мета: перевірити якість засвоєння програмних знань з теми та визна­чити рівень сформованості умінь і навичок.

Тип уроку: перевірка й корекція знань, умінь і навичок.

Хід уроку

I. Перевірка домашнього завдання

Зібрати робочі зошити з тематичним оцінюванням № 8.

II. Умови тематичної контрольної роботи № 8

Варіант 1

1°. Обчисліть:

1) 7,52 · 3,4; 2) 0,0018 · 8,7; 3) 45,921 · 100; 4) 42,1 : 100; 5) 36,48 : 12;

6) 8 : 32; 7) 8,41 : 29; 8) 4959 : 0,87; 9) 4 : 0,001.

2°. Знайдіть значення виразу: (20 – 22,05 : 2,1) · 6,4 + 9,2.

3°. Розв'яжіть рівняння: (х – 15,43) · 0,2 = 3,73.

4°. Відстань між двома селами дорівнює 149,8 км. З цих сіл одночасно в одному напрямку виїхали легковий автомобіль і мотоцикл, причому мотоцикліст їхав попереду. Через 3,5 год після початку руху авто­мобіль наздогнав мотоцикліста. Якою була швидкість мотоцикліста, якщо швидкість автомобіля дорівнювала 75,5 км/год?

5*. Якщо в деякому десятковому дробі перенести кому вправо через одну цифру, то він збільшиться на 61,047. Знайдіть цей дріб.

Варіант 2

1°. Обчисліть:

1) 9,45 · 7,4; 2) 0,0016 · 7,3; 3) 47,39 · 1000; 4) 47,9 : 100; 5) 65,39 : 13;

6) 9 : 36; 7) 10,01 : 9,1; 8) 14 : 0,56; 9) 18 : 0,01.

2°. Знайдіть значення виразу: 52 – (22,95 : 2,7 + 3,4) · 2,8.

3°. Розв'яжіть рівняння: 0,78 · (х + 0,12) = 3,9.

4°. З двох станцій, відстань між якими дорівнює 59,75 км, одночасно в одному напрямку виїхали пасажирський і швидкий поїзди. Попере­ду їхав пасажирський поїзд зі швидкістю 62,8 км/год і через 2,5 год після початку руху його наздогнав швидкий поїзд. Знайдіть швидкість швидкого поїзда.

5*. Якщо в деякому десятковому дробі перенести кому вправо через одну цифру, він збільшиться на 34,605. Знайдіть цей дріб.

Розв'язання і відповіді

Варіант 1

1°. 1) 24,65; 2) 0,01566; 3) 4592,1; 4) 0,421; 5) 3,04; 6) 0,25; 7) 0,29; 8) 5700; 9) 4000.

2°. .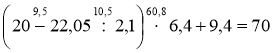

3°. х – 15,43 = 3,73 : 0,2; х – 15,43 = 18,65; х = 18,65 + 15,43; х = 34,08.

Відповідь. 34,08.

4°. Нехай х км/год — швидкість мотоцикліста, тоді (75,5 – х) км/год — швидкість наближення. За 3,5 год автомобіль і мотоцикліст наздогнали один одного, тобто подолали відстань, що розділяла їх (75,5 – х) · 3,5 км, яка за умовою задачі дорівнює 149,8 км. Складемо рівняння:

(75,5 – х) · 3,5 = 149,8;

75,5 – х = 149,8 : 3,5;

75,5 – х = 42,8;

х = 74,5 – 42,8;

х = 32,7.

Отже, швидкість мотоцикліста 32,7 км/год.

Відповідь. 3-2,7 км/год.

5*. Нехай х — шукане число, тоді нове число 10х, а їх різниця 10х – х за умовою дорівнює 61,047. Складемо і розв'яжемо рівняння:

10х – х = 61,047; 9х = 61,047; х = 61,047 : 9; х = 6,783.

Відповідь. 6,783.

Варіант 2

1°. 1) 69,93; 2) 0,01168;  3) 47390; 4) 0,479; 5) 5,03; 6) 0,25; 7) 1,1; 8) 25;      9) 1800.

2°. .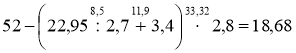

3°. 0,78 · (х + 0,12) = 3,9; х + 0,12 = 3,9 : 0,78; х + 0,12 = 5; х = 4,88. Відповідь. 4,88.

4°. Нехай х км/год — швидкість швидкого поїзда, тоді швидкість збли­ження (х – 62,8) км/год. За 2,5 год швидкий поїзд наздогнав пасажирсь­кий, отже, (х - 62,8) · 2,5 = 59,75; х – 62,8 = 59,75 : 2,5; х – 62,8 = 22,7; х = 22,7 + 62,8; х = 85,5. Отже, швидкість швидкого поїзда 85,5 км/год. Відповідь. 85,5 км/год.

5*. Нехай х — шуканий дріб, тоді новий дріб 10х, а їх різниця (10x – х) за умовою дорівнює 34,605. Складемо рівняння:

10х – х = 34,605; 9х = 34,605; х = 34,605 : 9; х = 3,845.

Відповідь. 3,845.