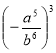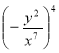Навчальний посібник "Алгебра 7 клас І семестр"
Посібник розроблений згідно Комбінованої системи М.П. Гузика і може бути використаний як додатковий матеріал для учнів на уроки. Він складається з трьох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу,
- між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу;
- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Ківерцівська експериментальна школа
Навчальний посібник

І семестр


Шановний семикласнику!
Ти починаєш вивчати новий шкільний предмет – алгебру.
Алгебра – це стародавня й мудра наука. Знайти її надзвичайно важливо. Алгебра – не тільки корисний, а й цікавий предмет, який розвиває кмітливість та логічне мислення. У цьому тобі допоможе навчальний посібник, який ти тримаєш в руках.
Посібник складається з трьох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу, на яких ти зможеш засвоїти поняття, терміни і правила блоку навчальної інформації, також навчитись застосовувати ці знання для розв’язування різноманітних задач і вправ.
-
між уроками фронтального опрацювання ти будеш виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені
- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Нехай Бог посилає тобі мудрості у вивченні алгебри!!!
Тема №1. Функції
Урок №1

Функції
«…поняття функціональної залежності є
основне поняття всієї вищої математики…»
О. Я. Хінчин
Питання
- Функція.
- Лінійна функція.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §3, пункти 20 – 23, стор. 132 – 172.
|
1. Функція |
||
|
1.1 |
Якщо кожному значенню незалежної змінної ( |
Периметр квадрата – функція від довжини його сторони. Шлях – функція від часу. |
|
1.2 |
Усі значення, яких набуває незалежна змінна (х, абсциса, аргумент), утворюють область визначення функції. |
|
|
1.3 |
Усі значення, яких набуває залежна змінна (у, ордината, функція), утворюють область значень функції. |
|
|
1.4 |
Графіком функції називають фігуру, яка складається з усіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – відповідним значенням функції. |
|
|
1.5 |
Способи задання функції:
|
|
|
1.6 |
Якщо функція описує реальний процес, то кажуть, що вона є математичною моделлю даного процесу. |
Зміна температури, шлях, зміна площі і т. д. |
|
2. Лінійна функція |
||
|
2.7 |
Функцію, яку можна задати формулою виду |
|
|
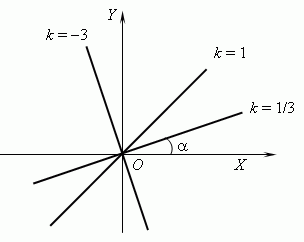
2.8 |
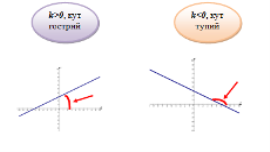
Від коефіцієнта k залежить кут, який утворює графік лінійної функції з додатним напрямком осі х, тому k називають кутовим коефіцієнтом прямої |
|
|
2.9 |
Властивості лінійної функції
|
|
|
2.10 |
Графіки функцій |
|
|
2.11 |
Функцію, яку задано формулою |
|
|
2.12 |
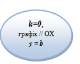
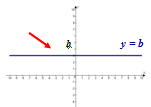
Графіком прямої пропорційності є пряма, яка проходить через початок координат. |
|
Урок №2
«Усе перевіряйте, чи воно
правильне, міцно тримайтесь того, що добре»
1 послання ап. Павла до солунян 5:21
Фронтальне опрацювання матеріалу
Функція. Область визначення і область значень функції. Способи задання функції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 1.6 блоку навчальної інформації № 1.
- Усно дайте відповіді на запитання:
-
Що називають функцією
- Що таке незалежна змінна?
- Що таке залежна змінна?
- Які є способи задання функції?
- Що таке область визначення і область значень функції?
- Що називають графіком функції?
- Що таке математична модель реального процесу?
Завдання 2.
- Усно розв’язати вправи, стор.136, 146 підручника: 760; 789.
- Виконати усно вправи, запропоновані вчителем у презентації.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово розв’язати вправи з вашого підручника, стор. 137 – 140: 765, 774, 795, 803.
Урок №3
«Якщо людина живе тільки для себе,
єдине, чого вона заслуговує – презирства»
Цицерон
Фронтальне опрацювання матеріалу
Графік функції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 1.6 блоку навчальної інформації № 1.
- Усно дайте відповіді на запитання:
- Як називається площина, на якій задано координатні прямі?
- Як називається вісь ОХ?
- Як називається вісь ОУ?
- На якій осі визначаються точки, що відповідають значенню аргументу?
- На якій осі визначаються точки, що відповідають значенню функції?
- Що називають функцією?
- Що називають графіком функції?
Завдання 2.
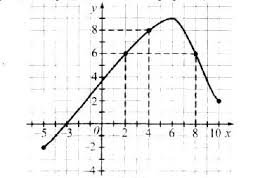
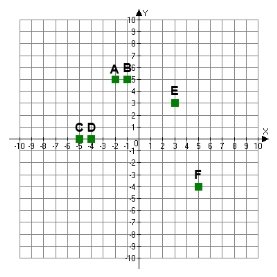
Визначити координати точок
|
|
A |
|
|
B |
|
|
|
C |
|
|
|
D |
|
|
|
E |
|
|
|
F |
|
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
|
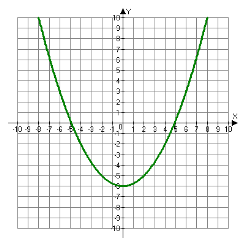
Задана функція: Знайдіть значення функції в даних точках і позначте ці точки на координатній площині. |
||||||||||||||||||||
|
- Знайдіть точки на графіку функції і заповніть таблицю
|
|
|
|
|
|
0 |
|
4 |
|
8 |
|
|
|
6 |
|
|
|
|
|
3 |
|
-
Побудуйте графік функції
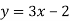
-
Побудуйте графік функції
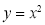
|
|
|
|
|
0 |
1 |
2 |
3 |
|
|
|
4 |
|
|
|
|
|
Урок №4
«Якщо людина живе тільки для себе,
єдине, чого вона заслуговує – презирства»
Цицерон
Фронтальне опрацювання матеріалу
Функція. Лінійна функція
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези блоку навчальної інформації № 1.
- Усно дайте відповіді на запитання:
- Що називають функцією?
- Що таке область визначення та область значень функції?
- Що називають графіком функції?
- Яка функція називається лінійною? Наведіть приклад.
- Що таке пряма пропорційність? Наведіть приклад.
- Що є графіком лінійної функції, прямої пропорційності?
- Вкажіть умови перетину та паралельності графіків лінійних функцій.
Завдання 2.
Усно виконати вправи:
- Нехай х см – довжина сторони рівностороннього трикутника, у – його периметр. Задайте формулою функцію у від х.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з наведених функцій не є лінійною?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Функцію задано формулою
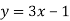
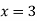
|
А |
Б |
В |
Г |
|
6 |
2 |
8 |
4 |
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Функцію задано формулою
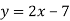
-
Функцію задано формулою
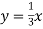 . При якому значенні аргументу значення функції дорівнює 12?
. При якому значенні аргументу значення функції дорівнює 12?
-
В одній системі координат побудувати графіки функцій
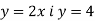
Завдання 4.
Письмово виконати вправи:
-
Функція задана формулою
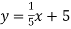 . Заповніть таблицю:
. Заповніть таблицю:
|
х |
|
– 15 |
|
1 |
|
– 1 |
|
у |
2 |
|
5 |
|
4 |
|
-
Побудувати графік функції
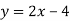
-
Не виконуючи побудови, знайдіть координати точки перетину графіків функцій
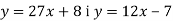
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Функцію задано формулою
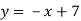
-
Функцію задано формулою
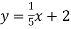 . При якому значенні аргументу значення функції дорівнює 7?
. При якому значенні аргументу значення функції дорівнює 7?
-
В одній системі координат побудувати графіки функцій
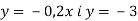
-
Функція задана формулою
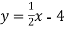 . Заповніть таблицю:
. Заповніть таблицю:
|
х |
– 8 |
|
– 2 |
|
6 |
|
|
у |
|
– 6 |
|
– 4 |
|
2 |
-
Побудувати графік функції
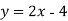
-
Не виконуючи побудови, знайдіть координати точки перетину графіків функцій
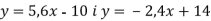
Завдання на вибір (виконані завдання здати на уроці індивідуального опрацювання):
- Підготувати 5 завдань «Функція. Лінійна функція».
- Скласти кросворд на 8 питань «Функція».
- Скласти розповідь «Наш туристичний похід» і намалювати графік руху туристів.
- Функція – це залежність. Складіть список речей, від яких залежить життя людини, доповніть його малюнками.
- Знайдіть кілька віршів з Біблії, де говориться, що ми залежимо від Бога.
Всі завдання повинні бути оформлені на стандартному листку А4, друковані, малюнки або намальовані від руки, або оформлені на комп’ютері у кольорі.
Урок №6
«Здобудеш освіту — побачиш більше світу»
Українське прислів’я
Внутрішньопредметне узагальнення матеріалу
Функція
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 1.
- Письмово відповісти на питання, запропоновані вчителем.
Завдання 2.
Усно виконати вправи:
- Укажіть вираз, що задає функцію.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Лінійну функцію задано формулою
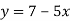
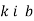
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з функцій є прямою пропорційністю?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Функцію задано формулою
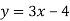
- значення функції, якщо значення аргументу дорівнює 4;
-
значення аргументу, при якому значення функції дорівнює
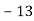
-
Функцію задано формулою
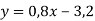
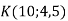
-
Побудуйте графік функції
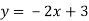
-
Функцію задано формулою
-
значення функції при
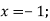
-
значення аргументу, при якому
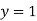
-
Побудуйте в одній системі координат графіки функцій:
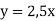
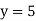
-
Знайдіть таке число b, щоб точка перетину графіків функцій
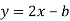
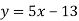
-
Побудуйте в одній системі координат графіки функцій:
Тема №2. Лінійні рівняння та їх системи
Урок №1

Лінійні рівняння та їх системи
«Алгебра – це, власне кажучи, аналіз рівнянь»
Жозеф Серре, французький математик
Питання
- Загальні відомості про рівняння.
- Лінійне рівняння з однією змінною.
- Лінійне рівняння з двома змінними.
- Системи двох лінійних рівнянь з двома змінними.
- Розв’язування задач за допомогою систем рівнянь.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §1, пункти 2 – 3, стор. 12 – 26; §4, пункти 24 – 29, стор. 173 – 218
|
1. Загальні відомості про рівняння |
||||||||||
|
1.1 |
Рівнянням називають рівність, що містить змінну. |
|
||||||||
|
1.2 |
Число, яке задовольняє рівняння, називають розв’язком або коренем рівняння. |
Число 2 є розв’язком рівняння |
||||||||
|
1.3 |
Розв’язати рівняння означає знайти його корені або довести, що їх немає. |
|||||||||
|
1.4 |
Два рівняння називаються рівносильними, якщо вони мають одні й ті ж самі корені. Рівносильними вважають і такі рівняння, які не мають коренів. |
|
||||||||
|
1.5 |
Властивості рівнянь:
|
|||||||||
|
2. Лінійне рівняння з однією змінною |
||||||||||
|
2.6 |
Рівняння виду |
|
||||||||
|
2.7 |
Числа |
|||||||||
|
2.8
|
Кількість коренів лінійного рівняння з однією змінною
|
|||||||||
|
3. Лінійне рівняння з двома змінними |
||||||||||
|
3.9 |
Лінійним рівнянням з двома змінними називають рівняння виду |
|
||||||||
|
3.10 |
Розв’язком рівняння з двома змінними називають пару значень змінних, для яких рівняння перетворюється у правильну рівність. |
1) (1; 2) 2) (3; 5) |
||||||||
|
3.11 |
Лінійні рівняння з двома змінними мають ті ж самі властивості, що і рівняння з однією змінною. |
|
||||||||
|
3.12 |
Графік рівняння з двома змінними утворюють усі точки координатної площини, координати яких є розв’язками даного рівняння. |
|||||||||
|
3.13 |
Графіком рівняння |
|||||||||
|
4. Системи двох лінійних рівнянь з двома змінними |
||||||||||
|
4.14 |
Якщо потрібно знайти спільні розв’язки двох рівнянь, то кажуть, що ці рівняння утворюють систему рівнянь. |
|
||||||||
|
4.15 |
Розв’язком системи двох рівнянь з двома змінними називають пару значень змінних, для яких кожне рівняння системи перетворюється у правильну числову рівність. |
(30; 26)
|
||||||||
|
4.16 |
Щоб розв’язати систему рівнянь графічним способом, потрібно побудувати графіки даних рівнянь в одній системі координат і знайти координати спільних точок цих графіків. |
|||||||||
|
4.17 |
Щоб розв’язати систему рівнянь способом підстановки, потрібно: 1) виразити з будь – якого рівняння системи одну змінну через іншу; 2) підставити в інше рівняння системи замість цієї змінної одержаний вираз; 3) розв’язати отримане рівняння з однією змінною; 4) знайти відповідне отриманому, значення першої змінної. |
Відповідь: (1; 2). |
||||||||
|
4.18 |
Щоб розв’язати систему рівнянь способом додавання потрібно: 1) помножити обидві частини рівнянь системи на такі числа, щоб коефіцієнти біля однієї зі змінних стали протилежними числами; 2) додати почленно ліві і праві частини рівнянь і замінити одне із рівнянь системи одержаним рівнянням; 3) розв’язати одержане рівняння з однією змінною; 4) знайти відповідне значення іншої змінної. |
Відповідь: (1; 2) |
||||||||
|
5. Розв’язування задач за допомогою систем рівнянь |
||||||||||
|
5.19 |
При розв’язуванні задач за допомогою систем рівнянь чинять так:
|
|||||||||
Урок №2
«Пам’ятайте, якщо ви бажаєте навчитися
плавати, то сміло заходьте у воду, а якщо бажаєте
навчитися розв’язувати задачі, то сміло розв’язуйте їх»
Дьордь Пойа, угорський, швейцарський, американський математик
Фронтальне опрацювання матеріалу
Загальні відомості про рівняння. Лінійне рівняння з однією змінною
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 2.8 блоку № 2.
- Усно дайте відповіді на запитання:
- Що називають рівнянням?
- Що називається коренем рівняння?
- Що означає розв’язати рівняння?
- Сформулювати основні властивості рівнянь.
- Сформулювати означення лінійного рівняння з однією змінною.
Завдання 2.
Виконати усно:
- Назвати ліву і праву частину рівняння:
- 5x + 7 = 3x – 2;
- 0,5x = 4,7х + 8;
-
4у + 12 = 0.
- Пояснити, чому не має розв’язку рівняння:
- х + 3 = х;
-
5 – z = 8 – z.
- Розв’язати рівняння:
![]()
![]()
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи, стор. 14 – 17 підручника: 34 (1, 3, 5); 41; 45; 49 (2, 4); 51 (1, 3, 5, 7, 9); 61 (1, 3); 62 (2); 63 (1).
Урок №3
«Неможливо правильно
керувати світом без Бога та Біблії»»
Джордж Вашингтон, 1-й президент США
Фронтальне опрацювання матеріалу
Розв’язування задач за допомогою лінійних рівнянь з однією змінною
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 2.8 блоку № 2.
- Усно дайте відповіді на запитання:
- Що називають рівнянням?
- Що називається коренем рівняння?
- Що означає розв’язати рівняння?
- Сформулювати основні властивості рівнянь.
- Сформулювати означення лінійного рівняння з однією змінною.
- Скільки розв’язків може мати лінійне рівняння і від чого це залежить?
Завдання 2.
- Прочитайте пункт 3, стор. 18 – 19 підручника.
- Усно дайте відповідь на питання:
- Що називають математичною моделлю реальної ситуації?
- За яким алгоритмом розв’язують задачі за допомогою лінійних рівнянь з однією змінною?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Назвіть невідомі величини
Позначте одну з них буквою;
Виразіть решту невідомих величин через ту, що позначили буквою
|
№ |
Фрагмент задачі |
Вираження невідомих |
|
1 |
У Василька і Марічки було грошей порівну |
Василько - |
|
Марічка - |
||
|
2 |
Один кілограм цукерок дорожчий за кілограм печива на 6 грн |
|
|
|
||
|
3 |
Пішохід прибув на 2 години пізніше, ніж велосипедист |
|
|
|
||
|
4 |
Один шматок дроту у 3 рази менший за другий |
|
|
|
||
|
5 |
Швидкість вантажівки на 48 км/год більша від швидкості легкової машини |
|
|
|
||
|
6 |
Віталій за день розв’язує 7 задач, а Мишко – 6. Скільки задач розв’яже кожен за х днів? |
|
|
|
Завдання 4.
Згадайте принци дії шалькових терез.
Допоможіть «відновити рівновагу» у наступних завданнях.
Відповідь:
Вираз А на 5 більший від виразу В А-5=В
Вираз В у 5р більший від виразу А 5А=В
Вираз А на 12 менший від виразу В А=В+12
Вираз В у 3р менший від виразу А А=3В
Вираз А у 10р більший від виразу В А=10В
Вираз В на 7 менший від виразу А А=В+7
Завдання 5.
- Для нового кабінету гімназії потрібно придбати комплект меблів: 15 парт та 30 стільців. Завгосп просить нас вказати ціну парти та стільця, якщо директор повідомила її, що загальна сума витрат складає 14 100 грн, а парта дорожча за стілець на 280 грн.
- Для ремонту гімназії було куплено фарбу. Завгосп відзначила, що маса однієї банки акрилової емульсії «Сніжка ULTRA BIEL» на 1,6 кг більша за масу однієї банки емалі ПФ-115, хоча 6 банок «Сніжки» має таку ж масу як і 14 банок емалі. Яка маса кожної банки?
- У комірчині стояло 2 мішки зі стартовою та фінішною шпаклівкою по 30 кг в кожному. Для ремонту з першого мішка взяли втричі більше шпаклівки, ніж з другого, після чого в ньому стало в 2 рази менше шпаклівки. Скільки залишилось матеріалу в кожному мішку?
- Улітку на річці Стир Роман і Кирил брали участь у районних змаганнях з плавання. У басейні гімназії Кирил пливе швидше на 0,2м/с ніж Роман. Відомо, що Роман за 25 с проплив на 1 м більше, ніж Кирил за 20 с. Яка швидкість кожного хлопця?
Урок №4
«Я все можу в Тім, Хто мене підкріпляє,
в Ісусі Христі»
До филип’ян 4:13
Фронтальне опрацювання матеріалу
Лінійне рівняння з двома змінними та його графік
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 3.12 блоку №2.
- Усно дайте відповідь на питання:
- Що називається розв’язком рівняння з двома змінними?
-
Чи є пара чисел (4;1) розв’язком рівняння
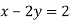
- Що називається графіком рівняння з двома змінними? Чи завжди таке рівняння має графік?
- Які рівняння називаються рівносильними? Яку властивість мають графіки рівносильних рівнянь?
- Серед даних рівнянь із двома змінними виберіть пари таких, що мають однакові графіки та поясніть, чому ви так вважаєте:
-
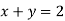
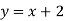
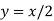
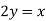
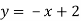
- Виконайте усно вправи:
- Серед поданих рівнянь назвіть лінійні рівняння з двома невідомими:
-
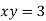
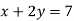
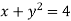 ; 4)
; 4) 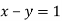
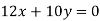
![]()
![]()
![]()
![]()
-
Назвіть кілька розв’язків лінійного рівняння
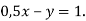
- Як на координатній площині розташований графік рівняння:
-
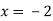
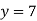
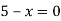
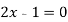
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Виконайте письмово вправи:
-
Які з пар чисел (2;2); (1;3); (1;3,5);
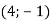
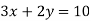
-
Виразіть
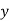
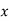
-
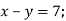
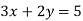
-
Які з точок
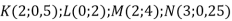 не належать графіку рівняння
не належать графіку рівняння 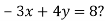
- Побудуйте графік рівняння:
-
Які з точок
-
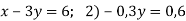
-
На прямій, яка є графіком рівняння
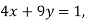
-
Знайдіть значення коефіцієнта
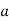
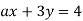
-
На прямій, яка є графіком рівняння
Урок №5
«А якщо кому з вас не стачає мудрості,нехай просить
від Бога, що всім дає просто, та не докоряє, – і буде вона йому дана»
Якова 1:5
Фронтальне опрацювання матеріалу
Системи лінійних рівнянь. Графічний спосіб розв’язування систем
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 4.16 блоку № 2.
- Усно дайте відповідь на питання:
- У якому випадку говорять, що треба розв’язати систему рівнянь?
- Що є розв’язком системи рівнянь з двома змінними?
- Що означає розв’язати систему рівнянь?
- У чому суть графічного методу розв’язування систем рівнянь з двома змінними?
- Що називають лінійним рівнянням з двома змінними?
- Які властивості рівнянь вам відомі?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Усно виконайте вправу 1007, стор. 194 підручника.
Завдання 3.
Письмово виконайте вправи, стор. 194 – 195 підручника: 1009 (2), 1010 (1, 3, 5), 1014 (1).
Завдання 4.
Письмово виконайте вправи:
-
На графіку рівняння
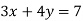
-
Знайдіть усі пари натуральних чисел, які є розв’язками рівняння
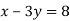
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
 Розв’яжіть рівняння
Розв’яжіть рівняння 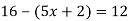 .
.
- У першій пачці в 5 раз більше зошитів, ніж у другій. Коли з першої пачки переклали у другу 12 зошитів, то в обох пачках зошитів стало порівну. Скільки їх було у кожній пачці спочатку?
-
Розв’яжіть графічно систему рівнянь
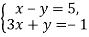
-
На графіку рівняння
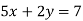
-
Знайдіть усі пари натуральних чисел, які є розв’язками рівняння
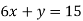
Урок №7
"Ні про що не турбуйтесь, а в усьому нехай
виявляються Богові ваші бажання молитвою
й проханням з подякою"
Филип'ян 4:6
Фронтальне опрацювання матеріалу
Розв’язування систем лінійних рівнянь способом підстановки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 4.14 – 4.17 блоку № 2.
- Усно дайте відповіді на запитання:
- Коли кажуть, що рівняння утворюють систему рівнянь?
- Що називають розв’язком системи лінійних рівнянь?
- Сформулюйте алгоритм розв’язування систем рівнянь способом підстановки.
- Як ви вважаєте, коли найкраще використовувати метод підстановки при розв’язуванні рівнянь?
Завдання 2.
Виконайте усно вправи
-
Чи є розв’язком системи
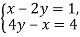 пара чисел:
пара чисел:
-
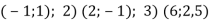 ?
?
-
Виразіть
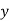
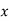
-
Виразіть
-
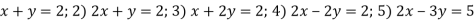
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконайте вправи:
-
Використовуючи алгоритми та приклади, розв’яжіть систему способом підстановки:
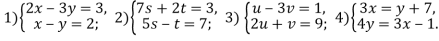
- Знайдіть координати точок перетину графіків рівнянь, не виконуючи побудов:
-
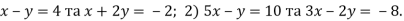
-
Знайдіть розв’язки системи рівнянь
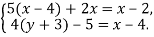
- Знайдіть помилку в розв’язанні:
-
Знайдіть розв’язки системи рівнянь
![]()
Відповідь: (3;2).
Завдання 4.
Заповніть пропуски так, щоб утворені записи були правильні (розв’язання системи способом підстановки):
![]()
Урок №8
«З ким поведешся, від того і наберешся»
Українське прислів’я
Фронтальне опрацювання матеріалу
Розв’язування систем лінійних рівнянь способом додавання
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 4.17 блоку №2.
- Усно дайте відповіді на питання:
- Скількома способами можна розв’язувати системи лінійних рівнянь з двома змінними?
- Що називають рівнянням?
- Що означає розв’язати рівняння?
- В чому суть методу підстановки розв’язування систем рівнянь?
- Коли виникає необхідність розв’язати систему рівнянь?
- Що називають розв’язком системи рівнянь з двома змінними?
- В чому суть методу додавання?
Завдання 2.
Виконайте усні вправи, запропоновані вчителем у презентації.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Виконайте письмово вправи зі ст. 202 – 205:
1047 (1, 3, 5), 1050 (2, 6), 1053 (1).
Урок №9
«Діяльність - єдиний шлях до знання»
Б. Шоу
Фронтальне опрацювання матеріалу
Розв’язування задач за допомогою систем рівнянь
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку №2.
- Завершіть речення:
- Рівність, яка містить невідоме, називається …
- Значення змінних, для яких рівняння перетворюється у правильну числову рівність, називається …
- Розв’язати рівняння означає …
- Якщо потрібно знайти спільні розв’язки двох чи кількох рівнянь, говорять, що ці рівняння утворюють …
- Математичною моделлю задачі є …
-
Як розв’язувати задачі за допомогою систем рівнянь?
- Що зайве? Чому?
а) «система, графік, змінна, розв’язок, спілкування»;
б) «показник, многочлен, степінь, гребінь »;
в) «рівність, рівняння, речення, тотожність»;
г) «число, значення, лікування, формула, задача»
Завдання 2.
Розгляньте приклад розв’язування задачі:
Учень задумав два числа, сума яких дорівнює 100, а різниця – 26. Які числа задумав учень?
Нехай х – перше число, тоді у – друге число. Оскільки їх сума дорівнює 100, то маємо рівняння: х + у = 100.
За другою умовою задачі маємо рівняння: х – у = 26.
Складемо систему рівнянь:
![]() та розв’яжемо способом додавання
та розв’яжемо способом додавання
2х = 126
х = 63
у = 37
Відповідь: перше число 63, друге – 37.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконайте вправи:
- Чи можна розміняти 100 грн. купюрами по 5 і 2 грн. так, щоб усіх купюр було 30?
- На двох складах 102 т цукру. Коли з першого складу забрали 15% цукру, то на ньому вже залишилося на 9 т цукру більше, ніж на другому. Скільки цукру було на кожному складі спочатку?
- Теплохід проходить за 2 год за течією річки й за 3 год проти течії 222 км. За 3 год за течією річки він проходить на 60 км більше, ніж за 2 год проти течії. Знайдіть швидкість теплохода в стоячій воді та швидкість течії річки.
- За 7 кг апельсинів і 4 кг лимонів заплатили 26 грн. Скільки коштує 1 кг апельсинів і скільки 1 кг лимонів, якщо 5 кг апельсинів дорожчі за 2 кг лимонів на 4 грн?
Урок №10
«Бог з нами навіть тоді, коли ми не бачимо Його»
Кирстен Холмберг, християнський журналіст
Фронтальне опрацювання матеріалу
Системи лінійних рівнянь з двома змінними
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 4.14 – 5.19 блоку № 2.
- Усно дайте відповідь на питання:
- Коли кажуть, що два рівняння утворюють систему рівнянь?
- Що є розв’язком системи двох рівнянь з двома змінними?
- Які способи розв’язування систем рівнянь вам відомі?
- Як розв’язати систему рівнянь графічним способом?
- Як розв’язати систему рівнянь способом підстановки?
- Як розв’язати систему рівнянь способом додавання?
- Як розв’язувати задачі за допомогою систем рівнянь?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Яке з поданих рівнянь має розв’язок (2; – 5)?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Яка пара чисел є розв’язком системи рівнянь
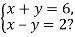
|
А |
Б |
В |
Г |
|
(4; 2) |
(3; 3) |
(2; 4) |
(6; 0) |
-
Яке рівняння дістанемо, якщо почленно додамо рівняння системи
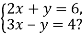
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
- Сума двох чисел дорівнює 75. Знайдіть ці числа, якщо 70% від одного і 40% від другого разом складають 42.
-
Розв’язати систему рівнянь способом підстановки:
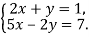
-
Розв’язати систему рівнянь способом додавання:
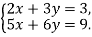
-
Розв’язати систему рівнянь:
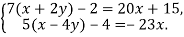
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Розв
 язати систему рівнянь способом додавання
язати систему рівнянь способом додавання 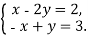
-
Розв
 язати систему рівнянь способом підстановки
язати систему рівнянь способом підстановки 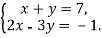
-
Розвяжіть систему рівнянь
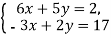 .
.
- 70% від одного числа на 20 більше за 60% від другого числа. Знайдіть ці числа, якщо їх сума дорівнює 75.
Урок №12
«Любов виникає з любові; коли хочу,
щоб мене любили, я сам перший люблю»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Лінійні рівняння та їх системи
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 2, звернувши особливу увагу на тези 1.1, 1.2, 1.3, 1.5, 2.6, 3.9, 3.10, 4.14, 4.15, 4.17, 4.18.
- Письмово відповісти на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Яке з рівнянь є лінійним рівнянням?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вкажіть розв’язок рівняння
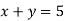
|
А |
Б |
В |
Г |
|
(– 5; 1) |
(5; 0) |
(– 5; 6) |
(– 4; 4) |
-
Запишіть пару чисел, яка є розв’язком системи
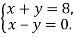
|
А |
Б |
В |
Г |
|
(6; 2) |
(4; 4) |
(5; 3) |
(8; 0) |
Завдання 3.
Письмово виконати вправи:
-
Розв’яжіть рівняння:
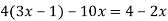 .
.
-
Розв’яжіть систему рівнянь способом підстановки
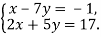
-
Розв’яжіть систему рівнянь
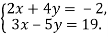
- Розв’яжіть задачу за допомогою рівняння:
На одному складі було в 3 рази більше телевізорів, ніж на другому. Після того, як з першого складу взяли 20 телевізорів, а на другий привезли 14, телевізорів на обох складах стало порівну. Скільки телевізорів було на кожному складі спочатку?
- Розв’яжіть задачу за допомогою системи рівнянь:
За 3 год за течією і 4 год проти течії катер проплив 174 км. За 4 год за течією і 5 год проти течії він проплив 224 км. Знайдіть власну швидкість катера і швидкість течії.
Тема №3. Цілі вирази. Степінь з натуральним показником. Одночлен
Урок №1

Цілі вирази. Степінь з натуральним показником. Одночлен
«Ледача рука до убозтва
веде, рука ж роботяща збагачує»
Книга приповістей Соломонових 10:4
Питання
- Вирази зі змінними. Цілі вирази.
- Тотожно рівні вирази. Тотожності.
- Степінь з натуральним показником.
- Властивості степеня з натуральним показником.
- Одночлен та його стандартний вигляд.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §2, пункти 4 – 7, стор. 27 - 53.
|
||
|
1.1 |
Виразом зі змінними називають вираз, утворений зі змінних, чисел, знаків дій і дужок. |
|
|
1.2 |
Значенням числового виразу, який одержимо, підставивши у вираз зі змінними замість змінних їхні значення, називають значенням виразу зі змінними |
Якщо
|
|
1.3 |
Вирази, які не містять дії ділення на вираз зі змінними, називають цілими. |
|
|
1.4 |
Вирази, які містять дію ділення на вираз зі змінними, називають дробовими. |
|
|
1.5 |
Вирази зі змінними використовують для запису формул |
|
|
||
|
2.6 |
Вирази, відповідні значення яких є рівними при будь-яких значеннях змінних, що входять до них, називають тотожно рівними. |
|
|
2.7 |
Рівність, яка є правильною для всіх значень змінних, називають тотожністю. |
|
|
2.8 |
Заміну одного виразу тотожно рівним йому виразом називають тотожним перетворенням виразу
|
|
|
2.9 |
При доведенні тотожностей використовують такі способи:
|
|
|
||
|
3.10 |
Степенем числа а з натуральним показником n, більшим за 1, називають добуток n множників, кожен з яких дорівнює a |
n разів
|
|
3.11 |
Степенем числа а з показником 1 називають саме число а. |
|
|
3.12 |
Степінь від’ємного числа з парним показником є число додатне. Степінь від’ємного числа з непарним показником є число від’ємне. |
|
|
3.13 |
Будь-який натуральний степінь числа 0 дорівнює 0. |
|
|
||
|
4.14 |
Щоб перемножити степені з однаковими основами, потрібно основу залишити ту саму, а показники степенів додати: |
|
|
4.15 |
Щоб поділити степені з однаковими основами, потрібно основу залишити ту саму, а від показника степеня діленого відняти показник степеня дільника: |
|
|
4.16 |
Щоб піднести степінь до степеня, потрібно основу залишити ту саму, а показники степенів перемножити: |
|
|
4.17 |
Щоб піднести до степеня добуток, досить піднести до цього степеня кожний множник і результати перемножити: |
|
|
||
|
5.18 |
Одночленом називають добуток чисел, змінних, та їхніх степенів. Змінні, числа та їхні степені також вважаються одночленами. |
|
|
5.19 |
Одночлен, записаний у вигляді добутку числового множника, який стоїть на першому місці, і степенів різних змінних, називають одночленом стандартного вигляду. |
|
|
5.20 |
Числовий множник одночлена, записаного у стандартному вигляді, називають коефіцієнтом одночлена. |
|
|
5.21 |
Степенем одночлена називають суму показників степенів усіх змінних, які входять до нього. Якщо одночленом є число, то вважають, що степінь такого одночлена дорівнює 0. |
|
Урок №2
«І все, що тільки чините,
робіть від душі, як Господу, а не людям»
Послання св. апостола Павла до Колосян 3 : 23
Фронтальне опрацювання матеріалу
Вирази зі змінними
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.5 блоку № 3.
- Усно дати відповідь на питання:
- Що називають виразом зі змінними?
- Що називають значенням виразу зі змінними?
- Дайте визначення цілого виразу. Наведіть приклади.
- Що називають дробовим виразом? Наведіть приклади дробових виразів.
- Де використовують вирази зі змінними?
Завдання 2.
Прочитайте вираз, використовуючи терміни «сума», «різниця», «квадрат», «куб» тощо.
-
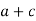
-
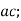
-
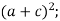
-
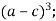
-
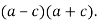
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
3.1. Заповніть таблицю, обчисливши значення виразу ![]() для заданих значень
для заданих значень ![]() :
:
|
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
3.2. Запишіть у вигляді виразу:
1) різницю чисел ![]() і
і ![]() ;
;
2) квадрат суми чисел ![]() і
і ![]() ;
;
3) суму куба числа ![]() і квадрата числа
і квадрата числа ![]() ;
;
4) квадрат різниці чисел ![]() і
і ![]() ;
;
5) різницю квадратів чисел ![]() і
і ![]() ;
;
6) півсуму добутку чисел 0,7 і ![]() та числа –0,6.
та числа –0,6.
3.3. Відомо, що ![]()
-
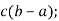
-
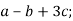
-
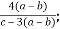
-
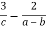 .
.
3.4. Складіть вираз для розв’язування задачі:
- Периметр прямокутника 16 см, одна з його сторін m см. Яка площа прямокутника?
-
З двох міст, відстань між якими S км, назустріч одне одному виїхали два автомобілі. Швидкість одного з них
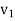 км/год, а швидкість другого –
км/год, а швидкість другого – 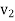 км/год. Через скільки годин вони зустрінуться?
км/год. Через скільки годин вони зустрінуться?
Урок №3
«Світ математики – це немовби багатоповерхова
будівля, причому ідеї кожного поверху зв’язані як між
собою, так і з тими, що знаходяться вище і нижче»
Годфрі Харолд Харді, англійський математик
Фронтальне опрацювання матеріалу
Тотожно рівні вирази. Тотожності
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.9 блоку № 3.
- Усно дай відповідь на питання:
- Що називають виразом зі змінними?
- Що називають значенням виразу зі змінними?
- Які вирази називаються тотожно рівними?
- Що називають тотожністю?
- Записані нижче рівності є тотожностями. Заповніть пропуски:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
- Якщо один із виразів замінити тотожно рівним йому виразом, то така заміна називається... перетворенням.
- Які прийоми використовують при доведенні тотожностей?
- Із запропонованих слів (словосполучень) утворіть пари, об’єднані певною (однією) логікою (змістом): 1) вирази; 2) тотожність; 3) заміна; 4) тотожно рівні; 5) рівність; 6) тотожне перетворення. Поясніть логіку.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Розглянь приклад 1 на стор. 29 підручника.
- Користуючись розглянутим прикладом, письмово виконай вправи, стор. 30 – 31 підручника: 134, 138 (1, 3, 5), 141, 142 (2, 3), 144 (1, 3).
Завдання 3.
- Розглянь приклад 2 на стор. 29 підручника.
- Користуючись розглянутим прикладом, письмово виконай вправу 144 (1, 3), стор. 31 підручника.
![]()
Готуємось до індивідуального опрацювання матеріалу
-
Спростіть вираз:
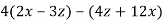 .
.
-
Доведіть тотожність:
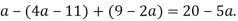
-
Спростити вираз і знайти його значення:
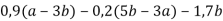 , якщо а = 2, b = 3.
, якщо а = 2, b = 3.
-
Доведіть тотожність
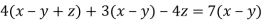 .
.
-
Доведіть тотожність:
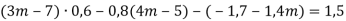 .
.
Урок №5
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Степінь з натуральним показником
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.10 – 3.13 блоку № 1.
- Усно дати відповідь на питання:
- Що називається степенем числа а з натуральним показником n?
- Що називають степенем числа а з показником 1?
- Чому дорівнює степінь від’ємного числа з парним і непарним показником степеня?
- Чому дорівнює будь-який натуральний степінь числа 0?
Завдання 2.
Уважно прочитайте повідомлення
Слово Exponent, яке ввів для показника степеня Штифель в 1553 році, означає «показник», » позивач». Показники степеня в сьогоднішньому вигляді ввів до науки Декарт (1637). Англієць за народженням, що жив у Франції, Юг писав 5аIV , Ерігон – 5а4, у Декарта ці символи перетворились в 5а4. Вираз «піднесення до степеня» вперше з’явився в 1716 році в роботі »Mathematische Lexicon» Вольфа.
Дайте відповіді на питання:
- Хто вперше ввів поняття степеня?
- Хто запропонував поняття «піднесення до степеня»?
- Кому ми завдячуємо сучасним виглядом показника степеня?
Завдання 3.
Усно виконати вправи (стор. 34 – 35): 152, 153.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 4.
Письмово виконати вправи (стор.36 – 38): 162, 165 (1, 3), 166 (2, 4, 6), 175, 177, 185.
Уроки № 6 – 8
«Не все те отрута, що неприємне на смак»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Властивості степеня з натуральним показником
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.10 – 4.17 блоку № 3.
- Усно дати відповідь на питання:
- Що називається степенем числа а з натуральним показником n?
- Що називають степенем числа а з показником 1?
- Чому дорівнює степінь від’ємного числа з парним і непарним показником степеня?
- Чому дорівнює будь-який натуральний степінь числа 0?
- Як перемножити степені з однаковими основами?
- Як поділити степені з однаковими основами?
- Як піднести степінь до степеня?
- Як піднести до степеня добуток?
Завдання 2.
- Усно виконати вправи (стор. 43): 205, 206, 208, 211.
-
Знайди значення виразу:
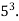
|
А |
Б |
В |
Г |
|
5 |
10 |
15 |
125 |
-
Подай у вигляді степеня добуток:
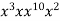 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Подай у вигляді степеня частку:
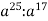 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
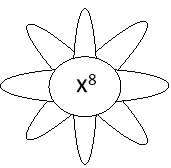 Користуючись різними властивостями степеня з натуральним показником, на пелюстках ромашки напишіть вирази, які б дорівнювали виразу усередині:
Користуючись різними властивостями степеня з натуральним показником, на пелюстках ромашки напишіть вирази, які б дорівнювали виразу усередині:
Письмово виконати вправи (стор. 43 – 45 ):
Завдання 4.
215, 220, 221 (1, 3, 5, 7), 224, 231.
Завдання 5.
|
1. Запишіть у вигляді степеня: |
||
|
1)
2) |
3) |
4) |
|
2. Спростіть вираз: |
||
|
1)
2) |
3) |
4) |
|
3. Знайдіть значення виразу: |
||
|
1)
2) |
3) |
4) |
|
4. Замініть зірочку степенем так, щоб утворилась правильна рівність: |
||
|
- |
а4 ∙ * : а13 = а2 |
- |
|
5. Піднесіть до степеня дріб: |
||
|
1)
2) |
3) |
4) |
|
6. Порівняйте: |
||
|
1) 85 та 214; 2) 1253 та 255;
|
3) 93 та 272 |
4)
|
Завдання 6.
236, 242.
Завдання 7.
-
Спростіть:
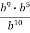 .
.
-
Обчислити, використовуючи властивості степеня:
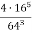 .
.
-
Знайдіть значення виразу:
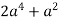 при
при 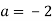
-
Спростити вираз: а)
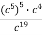 ; б)
; б) 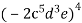 .
.
-
Обчислити, використовуючи властивості степеня:
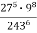 .
.
Завдання 8.
Письмово виконай вправи:
-
Виконай дії: 1)
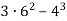 ; 2)
; 2) 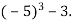
-
Спрости вираз: 1)
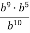 ; 2)
; 2) 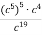 ; 3)
; 3) 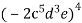 .
.
-
Обчисли, використовуючи властивості степеня: 1)
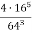 ; 2)
; 2) 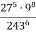 .
.
-
Знайди значення виразу
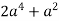 при
при 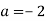
![]()
Готуємось до індивідуального опрацювання матеріалу
-
Виконайте дії: а)
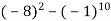 ; б)
; б) 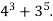
-
Спростіть:
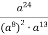 .
.
-
Обчислити, використовуючи властивості степеня:
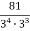 .
.
-
Знайдіть значення виразу:
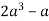 при
при 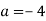
-
Спростити вираз: а)
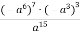 ; б)
; б) 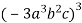 .
.
-
Обчислити, використовуючи властивості степеня:
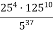 .
.
Уроки № 10, 11
«Визначай смак не по шкаралупі, а по ядру»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Одночлен. Стандартний вигляд одночлена
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити блок № 1.
- Усно дати відповідь на питання:
- Що називається степенем числа а з натуральним показником n?
- Що називають степенем числа а з показником 1?
- Чому дорівнює степінь від’ємного числа з парним і непарним показником степеня?
- Чому дорівнює будь-який натуральний степінь числа 0?
- Як перемножити степені з однаковими основами?
- Як поділити степені з однаковими основами?
- Як піднести степінь до степеня?
- Як піднести до степеня добуток?
- Що називається одночленом?
- Що таке стандартний вигляд одночлена?
- Що називають степенем одночлена?
- Що називають виразом зі змінними?
- Що називають значенням виразу зі змінними?
- Які вирази називаються тотожно рівними?
- Що називають тотожністю?
- Які прийоми використовують для доведення тотожностей?
Завдання 2.
Усно виконати вправи з підручника (стор. 50): 261, 262, 263.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи з підручника (стор. 50 – 52): 266, 268, 271 (1, 3, 5), 274, 276 (1, 3), 280 (1, 2, 6).
Завдання 4.
Письмово виконати вправи:
-
Звести одночлен до стандартного вигляду, вказати його коефіцієнт і степінь: 1)
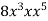 ; 2)
; 2) 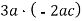 ; 3)
; 3) 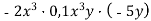 .
.
-
Знайдіть значення одночлена: 1)
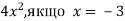 ;
;
2) ![]()
![]() ,
, ![]()
3) ![]() , якщо
, якщо ![]()
Завдання 5.
Письмово виконати вправи:
-
Знайдіть значення виразу:
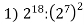 ; 2)
; 2) 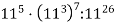 ; 3)
; 3) 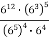 .
.
-
Знайдіть значення виразу: 1)
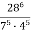 ; 2)
; 2) 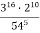 ; 3)
; 3) 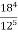 .
.
![]()
Готуємось до індивідуального опрацювання матеріалу
-
Обчисли значення одночлена
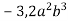 при
при 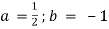 .
.
-
Спрости вираз: 1)
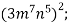 2)
2) 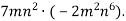
-
Запиши одночлен
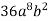 у вигляді квадрата одночлена.
у вигляді квадрата одночлена.
-
Спрости вираз: 1)
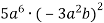 ; 2)
; 2) 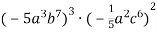 .
.
-
Подай вираз у вигляді куба одночлена
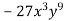 .
.
-
Спрости вираз:
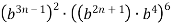 .
.
Урок № 13
«...найкраща помилка та, яку допускають при навчанні»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Цілі вирази. Степінь з натуральним показником. Одночлен
І. Засвоєння термінології до теми
Завдання 1.
- Повтори блок № 3, особливу увагу зверни на тези 1.1, 1.2, 3.10, 3.12, 4.14 – 5.19, 5.21.
- Письмово дай відповіді на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Запиши у вигляді степеня з основою
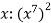 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Вкажи, який з поданих виразів не є цілим:
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисли значення виразу
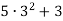 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Подай у стандартному вигляді одночлен:
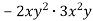 .
.
-
Виконай дії:
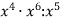 .
.
-
Спрости вираз:
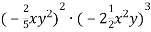 .
.
-
Доведи тотожність:
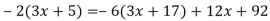 .
.
-
На першій полиці стоїть
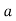
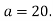
-
Спрости вираз
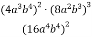 та знайди його значення при
та знайди його значення при 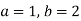
1


про публікацію авторської розробки
Додати розробку