Нестандартні задачі з математики (2 клас)
Методичний посібник – це збірник цікавих нестандартних задач з математики для учнів 2 класу. Матеріал підібрано відповідно до оновленої програми з математики в 2-ому класі. Його можна використовувати для здійснення індивідуального та диференційованого підходу як на уроках, так і в позаурочний час. Надаються відповіді до запропонованих задач.


![]()


З досвіду роботи Яшної Н.В., вчителя початкових класів Царичанської ЗОШ І-ІІІ ступенів Царичанської районної ради Дніпропетровської області
Затверджено рішенням науково-методичної ради КЗ «Царичанський районний методичний кабінет» Царичанської районної ради протокол № від
Рецензенти:
Логвиненко Н.Д. – методист КЗ «Царичанський районний методичний кабінет»; Рашевська Т.В.- директор Царичанської ЗОШ І-ІІІ ступенів


З досвіду роботи Яшної Н.В., вчителя початкових класів КЗ «Царичанської ЗОШ І-ІІІ ступенів» Царичанської селищної ради Дніпропетровської області
Методичний посібник – це збірник цікавих нестандартних задач з математики для учнів 2 класу. Матеріал підібрано відповідно до оновленої програми з математики в 2-ому класі. Його можна використовувати для здійснення індивідуального та диференційованого підходу як на уроках, так і в позаурочний час. Надаються відповіді до запропонованих задач.
Посібник адресований вчителям початкових класів, другокласникам та їхнім батькам.
Обсяг посібника 35 сторінок
КЗ «Царичанська загальноосвітня школа І-ІІІ ступенів»
Царичанської селищної ради
Дніпропетровської області
смт. Царичанка
вул. Соборна, 40а
51000
E-mail: Tcarihanka@gmail
Зміст
Передмова ………………………………………………………………………….4
Задачі на обчислення ……………………………………………………………...6
Задачі на поєднання арифметичних дій………………………………………….7
Задачі на знаходження невідомих за сумою і різницею………………………..7
Задачі на відношення між величинами:
Вікові зміни.………………………………………………………………………9
Часові залежності…………………………………………………………………10
Логіка з геометрії…………………………………………………………………11
Позиційні задачі…………………………………………………………………..13
Задачі на вилучення………………………………………………………………14
Логічні задачі………………………………………………..................................16
Комбінаторні задачі………………………………………………………………20
Задачі на переливання……………………………………………………………21
Відповіді на задачі ……………………………………………………………….22
Використана література ………………………………………………………....34

 Передмова
Передмова
« Рано чи пізно кожна правильна
математична ідея знайде своє
застосування в тій чи іншій справі.»
(О.М.Крилов)
В основі оновлення й перебудови шкільної освіти Державним стандартом передбачається одна з найголовніших задач школи - підготовка всебічно розвиненої, активної особистості, здібної до самостійних досліджень і відкриттів.
Нестандартні задачі становлять один із напрямів розвитку математичного мислення, формування досвіду творчої діяльності молодших школярів, допомагають знаходити правильне розв’язання проблеми, застосовувати знання на практиці, переносити відомі їм способи дій у нові для них ситуації та відкривати нові способи діяльності.
У посібнику містяться цікаві, різні за складністю завдання, що охоплюють програмовий матеріал з математики для 2 класу. Пропоновані задачі розвивають логічне, дивергентне мислення, творчу уяву, заохочують до творчого пошуку, формують вміння самостійно приймати рішення. Зміст кожної задачі з логічним навантаженням дає змогу учням включатися в пошук, робити дотепні умовиводи, цілісно і синтетично уявити і, завдяки цьому вникнути в ситуацію, збуджують пізнавальний інтерес, вчать дітей обґрунтовувати свої відповіді, будувати логічну послідовність своїх висловлювань. Через упровадження нестандартних завдань виховується в учнів пізнавальний інтерес до вивчення математики, формуються інтелектуальні здібності.
Пошукова спрямованість завдань, виховання у дітей бажання знайти відповідь самостійно допоможуть учням навчитися співставляти, порівнювати, аналізувати, встановлювати закономірності.
Для того, щоб розв’язати навіть дуже складну задачу, учням знадобляться знання, що не виходять за межі шкільної програми. Задачі можна використовувати для роботи як із дітьми, що виявляють особливу цікавість до математики, так і з учнями, які прагнуть проявити кмітливість.
До збірки включено відповіді та детальні розв’язання до деяких задач. Посібник корисний для використання і на уроках, і під час проведення математичних змагань, олімпіад, для організації диференційованої домашньої роботи школярів.

 Задачі на обчислення
Задачі на обчислення
Задачі на логіку нумерації
- Записати число третього десятка, яке парне і ділиться на 7.
- Записати число п’ятого десятка, яке непарне і ділиться на 9.
- Записати парне двоцифрове число і, щоб кількість десятків була на 6 більша, ніж кількість одиниць.
- Записати двоцифрове непарне число, яке більше 39 і менше 43.
- Назвати найбільше парне двоцифрове число.
- Сума цифр двоцифрового числа дорiвнює найбiльшому одноцифровому, а число десяткiв – на 1 менше вiд цiєї суми.
- Над пiд`їздом будинку висить таблиця – покажчик квартир – з числами 33 - 48. Чи є в цьому пiд`їздi квартири 30, 39, 41, 51?
- Є двi групи чисел: 11, 21, 35, 47, 14 та 11, 12, 53, 43, 18. Назви всi рiзнi числа, якi входять до цих груп.
- Володя назвав усi числа другого десятка, а Михась – усi двоцифровi числа, кожне з яких записується двома однаковими цифрами. Якi числа назвав Володя, а якi Михась?
- Галинка написала всi числа по порядку вiд 1 до 99. Скiльки раз вона написала цифру 7?
- У потязі 14 вагонів. Дівчинка сіла у сьомий вагон. Скільки вагонів попереду цього вагона і скільки вагонів позаду нього?
- Скільки аркушів між п’ятим і вісімнадцятим аркушами книжки?

 Задачі на поєднання арифметичних дій
Задачі на поєднання арифметичних дій
Між показниками одного об’єкта
- Максиму три роки тому було 3 роки. Скільки йому буде років через три роки?
- Відрізок збільшили на 6 см і він став втричі довший. Якої довжини був відрізок спочатку?
- Через 6 років Петрик буде вчетверо старший, ніж він є зараз. Скільки років Петрику зараз?
- У бідон долили третину того молока, яке було у бідоні. Скільки літрів молока було спочатку у бідоні, якщо стало 28 літрів?
- Від стрічки відрізали її четверту частину. Скільки сантиметрів стрічки відрізали, якщо залишилось 60 см стрічки?
- До бочки долили спочатку 17 л води, а потім відлили третю частину води, яка була у бочці, або 16 л. Скільки літрів води спочатку було у бочці?
- До ящика спочатку доклали 8 апельсинів, а потім забрали 11 апельсинів. Скільки апельсинів було спочатку у ящику, якщо їх стало 25?

Задачі на знаходження невідомих за сумою і різницею
У даних задачах один із доданків на кілька одиниць більший (менший), ніж другий. Щоб розв’язати дані задачі, ми спочатку урівняємо доданки: до результату суми додамо (чи віднімемо) результат різниці між доданками. Потім результат суми зрівняних доданків розділити на 2 – знайдемо один із доданків, а потім, за умовою задачі, знайдемо другий доданок.
- У Вови та Олі разом було 30 листівок. У Олі було на 4 листівки більше, ніж у Вови. Скільки марок було у кожної дитини?
- У двох гусок 12 гусенят. У першої на 4 більше, ніж у другої. Скільки гусенят у кожної гуски?
- Діти назбирали два кошики слив. У першому кошику на 6 слив менше, ніж у другому. Скільки слив у кожному кошику, якщо всього зібрано 30 слив?
- Під час ремонту даху використали 12 кг жовтої і білої фарби. Жовтої фарби пішло на 4 кг більше, ніж білої. Скільки кілограмів жовтої та білої фарби використали окремо?
- Господар купив на ринкові 35 кг моркви та цибулі. Скільки він купив цибулі, якщо моркви на 9 кг менше?
- Хлопчик і дівчинка виготовили 15 кружечків. Скільки кружечків виготовив кожний з них, якщо відомо, що хлопчик виготовив на 5 кружечків більше?
- На трьох кущах розквітло 28 троянд. На другому кущі розквітло на 3 троянди більше, ніж на першому, а на третьому – на 4 троянди більше, ніж на другому. Скільки троянд розквітло на кожному кущі?
- У трьох господинь 67 кг яблук. У другої – на 5 кг менше, ніж у першої. У третьої – на 12 кг яблук більше, ніж у першої. Скільки кілограмів яблук у кожної господині?
- У двох коробках 22 олівці. У першій коробці на 2 олівці більше, ніж у другій. Скільки олівців у кожній коробці?
- У двох кошиках 75 персиків. Коли з першого взяли 6, а з другого 9, то у кошиках залишилося персиків порівну. Скільки персиків у кожному кошику?

Задачі із відношеннями між величинами
Вікові зміни
- Якщо брату 4 роки і він молодший від своєї сестри на 4 роки, то скільки буде років сестрі через чотири роки?
- Якщо брату два роки тому було 9 років і він на шість років молодший від сестри, то скільки років сестрі зараз?
- Якщо сестра молодша за брата на п’ять років і через три роки її вік складатиме 12 років, то якого віку брат?
- Якщо чотири роки тому вік сестри складав 8 років і вона молодша від брата на чотири роки, то скільки років братові зараз?
- Дідові 64 роки, його синові 40 років, а онукові – 12. Через скільки років вік діда дорівнюватиме сумі років сина і онука?
- Сергій на запитання, скільки йому років, відповів, що йому разом з Петриком тепер 36 років, а 6 років тому він був старший за Петрика утричі. Скільки років Сергієві тепер?
- Марії і Олені разом 16 років, а через 4 роки Олена буде втричі старша за Марію. Скільки років кожній дівчинці тепер?
- Сестра старша від брата на п'ять років. На скільки років вона буде старша від брата через шість років?
- Брат на запитання, скiльки йому рокiв, вiдповiв : "Менi разом з сестрою 19 рокiв, а 5 рокiв тому я був удвiчi старший вiд неї." Скiльки рокiв йому тепер?
- Яка з календарних пiр року - весна, лiто, осiнь, зима - найкоротша? Чи завжди вона найкоротша ?
- Три дiвчинки на запитання скiльки рокiв кожнiй, вiдповiли:
– Нам разом 25 рокiв.
– Я старша за Наталку на 1 рiк.
– Менi разом з Тетянкою 17 рокiв.
Скiльки рокiв кожнiй дiвчинцi?
12. Учень лягає спати о дев’ятій годині вечора, а будильник заводить на сьому ранку. Скільки годин спатиме учень?

Часові залежності
- Що вчора було "завтра", а "завтра" стане "вчора"?
- Сьогодні п'ятниця. Який день тижня буде через шість днів?
- Якщо наступного дня після свого дня народження я скажу: "Післязавтра буде середа", то в який день тижня у мене день народження?
- Весняні канікули розпочалися 23 березня і закінчилися 31 березня. Оксана сказала, що відпочивала 8 днів. Чи правильно вона полічила кількість днів?
- За якою ознакою складено рядки слiв:
а) ранок, день, вечір, нiч;
б) весна, лiто, осiнь, зима;
в) вересень, жовтень, листопад;
г) доба, тиждень, мiсяць, квартал.

 Логіка з геометрії
Логіка з геометрії
- Вовк і Лисиця – сусіди по дачі. Довжина спільної сторони дачі 12 метрів. Цю сторону Лисиця загородила парканом, закопуючи через кожні 2 метри стовп. Скільки всього знадобилось стовпів?
- Кришка столу має 4 кути. Один кут відрізали. Скільки тепер кутів у стола?
- Шість стовпів для огорожі ділянки розміщено в один ряд. Відстань між двома сусідніми стовпами 5 м. Скільки метрів становить відстань між крайніми стовпами?
- З яких геометричних фігур складено зображення? Полічи і напиши, скільки:

- З яких геометричних фігур складено зображення? Полічи і напиши, скільки:
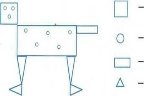
-

 З яких геометричних фігур складено зображення? Полічи і напиши, скільки:
З яких геометричних фігур складено зображення? Полічи і напиши, скільки:
![]()
![]()
![]()
![]() -
-
![]()
![]()
![]()
![]()
![]()
![]() -
-
-
 -
-
![]()
![]()
- У зображеній фігурі перекладіть 4 сірники так, щоб вийшло 10 квадратів.

- З 10 сірників склали будинок. Треба повернути будинок іншою стороною, переклавши 2 сірника.

- «Келих" (див. лівий малюнок), і "чарка" (див. правий малюнок) складені із чотирьох сірників. Усередині кожної "посудини" - вишенька. Як потрібно перемістити "келих" і "чарку", переклавши по два сірники в кожному з них, щоб вишеньки виявилися зовні?
![]()
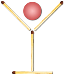
- Маємо стрілу, таку, як показана на малюнку.
Завдання:
1) перекладіть 8 сірників, щоб вийшло 8 рівних трикутників.
2) перекладіть 7 сірників так, щоб одержати 5 рівних чотирикутників.
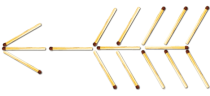
- На малюнку ви бачите корову, у якої є все, що має бути: голова, тулуб, ноги, роги та хвіст. Корова на малюнку дивиться вліво. Перекладіть рівно два сірники так, щоб вона дивилася вправо.
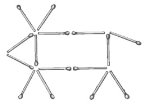
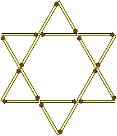
- Переставте 2 сірники з 18 так, щоб замість 8 трикутників фігура стала складатися з 6 трикутників. Повинні вийти тільки трикутники й не повинне бути вільно висячих сірників.
- Переставте 3 сірники так, щоб рибка попливла в другу сторону.

- Сірниковий рак повзе вправу сторону, переставте 3 сірники, щоб він повз вліво.

Позиційні задачі
- Якщо трикутник перший справа, а прямокутник перший зліва, то як будуть розташовані фігури зліва направо?
- Якщо круг перший справа, а трикутник – не другий зліва, то як будуть розташовані фігури справа наліво?
- Розфарбувати чотири квадрати так, щоб червоний квадрат лежав між зеленим та жовтим, а зелений – між синім та червоним. Назвати кольори квадратів зліва направо.
- Розфарбувати квадрат, трикутник, прямокутник, коло трьома кольорами (червоним, синім, зеленим) та розмістити так, щоб червона фігура знаходилася між прямокутником та синьою фігурою і фігури одного кольору поряд не стояли. Назвати фігури справа наліво.
- Розфарбувати квадрат, трикутник, шестикутник, овал чотирма кольорами (червоним, синім, жовтим, зеленим) та розмістити так, щоб червона фігура знаходилась між трикутником та синьою фігурою, а жовта фігура між червоною та овалом. Перша зліва фігура не квадрат. Назви фігури справа наліво.
- Розфарбувати п’ятикутник, овал, трикутник, чотирикутник двома кольорами (червоним, синім) та розмістити їх так, щоб фігури одного кольору поряд не знаходилися, трикутник лежав між п’ятикутником та червоним чотирикутником, а першою справа фігура була не овал. Назвати фігури справа наліво.

Задачі на вилучення
- У виставі "Ріпка" взяли участь Оля, Павлик, Марійка та Сергіко. Вони виконували ролі мишки, жабки, ведмедя і кабана. Мишкою була одна з дівчаток, але не Оля. Павлик не жабка і не ведмідь, Сергійко теж не жабка. Яку роль виконувала у виставі кожна дитина?
|
|
Мишка |
Жабка |
Ведмідь |
Кабан |
|
Оля |
|
|
|
|
|
Павлик |
|
|
|
|
|
Марійка |
|
|
|
|
|
Сергійко |
|
|
|
|
- Чотири катери: "Альбатрос", "Бригантина", "Вихор" та "Глобус" відходять від причалу в різний час. "Альбатрос" відходить не першим, але раніше за "Вихор" та "Глобус", а "Глобус" не раніше за "Вихор". Розмісти назви катерів у тому порядку, в якому вони відходять від причалу.
Розв'яжи задачу, скориставшись таблицею типу: тут потрібно викреслювати "зайве".
|
"Альбатрос" |
1 |
2 |
3 |
4 |
|
"Бригантина" |
1 |
2 |
3 |
4 |
|
"Вихор" |
1 |
2 |
3 |
4 |
|
"Глобус" |
1 |
2 |
3 |
4 |
3. На змаганнях з художньої гімнастики Галинка, Жанна і Наталка зайняли призові місця й одержали золоту, срібну і бронзову медалі. Жанна одержала не золоту медаль, а Галинка не бронзову. Наталка здобула не срібну, а Жанна не бронзову медаль. Яку медаль отримала кожна дівчинка?
|
|
золота |
срібна |
бронзова |
|
Галинка |
|
|
|
|
Жанна |
|
|
|
|
Наталка |
|
|
|
4. На вулиці, утворивши коло, розмовляють 4 хлопчики: Іван, Василь, Гліб і Микола. Хлопчик в зеленій сорочці (не Іван і не Василь) стоїть між хлопчиком в блакитній сорочці і Миколою. Хлопчик в білій сорочці стоїть між хлопчиком в червоній сорочці і Василем. Яку сорочку носить кожен хлопчик?
|
|
зелена |
блакитна |
червона |
біла |
|
Іван |
|
|
|
|
|
Василь |
|
|
|
|
|
Гліб |
|
|
|
|
|
Микола |
|
|
|
|
 Логічні задачі
Логічні задачі
- У тварини дві праві лапи, дві ліві лапи, дві лапи попереду, дві позаду. Скільки ніг у тварини?
- Кухар насипав рис порівну у дві склянки. Потім він з однієї склянки пересипав рис у каструлю. Де рису більше: у каструлі чи у склянці?
- Скільки кінців у кілка? У 2 кілків? УУ двох з половиною?
- Летіла зграя гусей: одна гуска попереду, а дві позаду; одна позаду і дві попереду, одна гуска між двома і три в ряд. Скільки було всього гусей?
- На столі лежали 3 цукерки в одній кучці. Дві матері, дві дочки та бабуся з внучкою взяли цукерки по одній штучці, і не стало цієї кучки. Як це зрозуміти? Скільки людей брали цукерки?
- На галявині гралися зайці. Всього у них 18 вух. 4 зайці сховалися. Скільки зайців залишилося. Скільки в них лап?
- У бджілки оченят стільки, скільки й у тебе, та ще стільки ж та ще півстільки. Скільки оченят у бджілки?
- Кіт живе 5 років, а півень – 3 роки. Скільки років можуть жити в господарки разом кіт і півень?
- Зустрілися п’ять чоловіків. Кожен за руку привітався з кожним. Скільки всього відбулося рукостискань?
- Двоє домовилось сісти у 9-ий вагон поїзда. Але один сів у 9-й вагон з кінця, а другий – у 9-й вагон з початку поїзда. Скільки має бути вагонів у поїзді, щоб пасажири насправді зустрілися в 9-ому вагоні?
- У Андрія і Бориса разом 11 горіхів. У Андрія і Володі – 12 горіхів, у Борі і Володі – 13 горіхів. Скільки всього горіхів у Андрія, Бориса і Володі разом?
- В одній сім’ї два батька й два сини. Скільки це чоловіків?
- Три курки за три дні знесуть три яйця. Скільки яєць знесуть 6 курок за 6 днів?
- Червона Шапочка несла бабусі 14 пиріжків: з м’ясом, грибами і капустою. Пиріжків із капустою було найбільше, причому їх було вдвічі більше, ніж пиріжків із м’ясом, а пиріжків із м’ясом було менше, ніж пиріжків із грибами. Скільки було пиріжків із грибами?
- Летіло 5 страусів. Одного страуса підстрелив мисливець. Скільки страусів полетіло далі?
- Співучий півник на вазі
Стояв лиш на одній нозі.
І мав вагу той півник – 2 кілограми рівно.
А ось яку б вагу мав птах,
Якби стояв на двох ногах?
- Хлопчик зібрав у коробку павуків і жуків – усього 8 штук. Якщо полічити, скільки всього лап у коробці, то виявиться 54 лапи. Скільки в коробці жуків і скільки павуків?
- У мене сестер і братів порівну. А в моєї сестри вдвічі менше сестер, ніж братів. Скільки нас?
- У восьминога 8 лап. Трьома парами лап він міцно тримає трьох водолазів. Скільки пар його лап ледарюють?
- Два батька і два сини взялися поділити три апельсина. По скільки апельсин отримав кожен?
- Висота дуба 20 м. За день мурашка піднімається по ньому на 5 м вгору, а за ніч спускається на 4 м вниз. За скільки днів мурашка доповзе до вершини дуба?
- Шість однакових бочок уміщують 28 відер води. Скільки відер води уміщують 15 таких бочок?
- Є шматок шовку довжиною 8 м. Як , не користуючись метром (чи іншою міркою довжини), відрізати від нього 6 м?
- Від рулону тканини довжиною 56 м відрізають по 7 м. Скільки розрізів треба зробити, щоб поділити на рівні шматки всю тканину?
- Як у кімнаті можна поставити 2 стільці, щоб біля кожної стіни стояло по 1 стільцю?
- Батько і діти їхали на велосипедах. У всіх велосипедах було 7 коліс. Скільки серед цих велосипедів було триколісних і скільки двоколісних?
- У дворі були кури й поросята. У них всіх 5 голів, а лап 14. Скільки було курей і поросят?
- Як розмістити 6 стільців біля 4 стін, щоб біля кожної стіни було тільки по 2 стільці?
- Розставте 9 стільців у кімнаті так, щоб біля кожної стіни стояло 3 стільці.
- Розмістити 8 стільців у кімнаті так, щоб біля кожної стіни стояло 3 стільці.
- Чоловікові треба перевезти через річку прирученого вовка, козу і капусту. Човен настільки малий, що в ньому можуть поміститися лише чоловік і з ним або вовк, або коза, або капуста. Зрозуміло, що козу не можна залишити на березі з вовком, а капусту – з козою. Що робити чоловікові?
- У матері п’ятеро дочок, у кожної по одному брату. Скільки всього дітей у матері?
- Шість мавп вирішили стати футболістами. Але оскільки всі вони хочуть бути лише воротарями, то на місце решти гравців надумали запросити страусів. Скільки страусів їм потрібно покликати. щоб усім було місце в командах, якщо в команді повинно бути 11 гравців, а воротар потрібен тільки один?
- Троє рибалок пішли ловити рибу і впіймали рибу-пилу, рибу-молот і меч-рибу. Меч-риба довша за рибу-молот і коротша за рибу-пилу. Яка риба серед них найдовша?
- У Бабусі-Ягусі завелося 6 мишей. Кожна миша згризає за зиму 5 шкарпеток. Скільки шкарпеток потрібно сплести Бабусі-Ягусі, щоб навесні було в чому вийти на вулицю?
- Мама поставила на стіл 9 склянок, з них перевернула дві склянки. Скільки склянок стало на столі?
- Фрекен Бок спекла пампушки. Прилетів Карлсон і з’їв половину. Потім Малюк з’їв половину того, що залишилось, і на тарелі лишилось 2 пампушки. Скільки усього пампушок спекла Фрекен Бок?
- Слимак почав підніматись по стіні в понеділок зранку. Висота стіни — 10 м. Слимак піднімається на 2 метри за один день і спускається на 1 метр за ніч. У який день тижня слимак доповзе до верхнього краю стіни?
- Летіли галки, побачили палки. Якщо на кожну палку сяде по галці, то для однієї галки не вистачить палки. А якщо на кожну палку сяде по дві галки, то одна з палок залишиться без галок. Скільки було галок і скільки було палок?
- У двох дівчаток разом 11 олівців. Якби в однієї з них стало на 5 олівців більше, то вона мала б у три рази більше олівців, ніж друга дівчинка. Скільки олівців у кожної дівчинки?
- Троє хлопчиків зробили 16 паперових корабликів, причому другий зробив на 2 кораблики менше, ніж перший, а третій – на 5 корабликів більше, ніж другий. Скільки корабликів зробив кожний хлопчик?

Комбінаторні задачі
Комбінаторика – це розділ математики, у якому вивчають питання про те, скільки різних комбінацій, які задовольняють ті чи інші умови, можна скласти із заданих об’єктів.
- У фінальному забігу на 50 м беруть участь Іваненко, Сидоренко, Коноплянко. Назвіть можливі варіанти розподілу призових місць. Скільки таких варіантів існує?
- На столі лежать яблуко, банан, груша. Скільки існує різних способів з\їсти фрукти?
- Туристи здійснюють подорож до гірського озера. Перший етап шляху можна подолати електропотягом або автобусом, другий — човнами, велосипедами або пішки. Скільки існує можливих способів здійснення подорожі?
- Хлопчик запланував купити книжку, альбом, ручку, гумку. А потім вирішив купити лише два предмети. Що міг купити хлопчик?
- На свято до Мухи-Цокотухи завітали Комар, Таракан, Блошка, Жук. Муха запросили всіх танцювати. Які пари могли утворитися?
- У ляльковому гуртку 4 дівчинки і 4 хлопчики. На екскурсію пішло 5 дітей. Скільки могло бути серед них дівчаток і хлопчиків?

 Задачі на переливання
Задачі на переливання
Задачі на переливання рідини можна розв’язувати
двома способами: з кінця і в переборі різних
варіантів переливань.
- Як за допомогою 5-літрового бідона і 3-літрової банки набрати на березі річки 4л води?
- Десятилітровий бідон наповнений водою. Як за допомогою семилітрового і трилітрового порожніх бідонів відміряти 5 літрів?
- У Карлсона є відро варення, воно вміщає 7 літрів. У нього є 2 порожніх відерка - 4-літрове і 3-літрове. Допоможіть Карлсону відлити 1 літр варення до чаю в менше (3-літрове) відерко, залишивши 6 літрів у великому (7-літровому) відрі.
- Губці Бобу терміново потрібно налити з водопровідного крану 6 л води. Але він має лише дві посудини: 5-літрову і 7-літрову. Як йому це зробити?
- Як Маші за допомогою 7-літового відра та 3-літрової банки налити в каструлю 5 л води, щоб зварити кашу?
Відповіді до задач:
Задачі на логіку нумерації
- 28.
- 45
- 82.
- 41.
- 98.
- 89.
- 30, 51 немає.
- 21, 35, 47, 14, 12, 53, 43, 18
- Володя - вiд 11 до 20, Михась - 11, 22,..., 99
- 11 разів.
- Спереду 6 вагонів, а позаду 14-7=7 (вагонів)
- (18-5)-1=12 (аркушів)
Задачі на поєднання арифметичних дій
Між показниками одного об’єкта
- Відповідь: 9 років.
- Відповідь: 3 см.
- Відповідь: 2 роки.
- Відповідь: 21 літр.
- Відповідь: 20 см.
- Відповідь: 31 л.
- Відповідь: 28.
Задачі на знаходження невідомих за сумою і різницею
- 30 – 4 =26 листівок разом, якщо у Олі та Вови їх порівну. 26:2=13 листівок у Вови, а у Олі, за умовою задачі, 13+4=17 марок. Можна урівняти листівки Вови з листівками Олі: 30+4=34, потім 34:2=17 листівок у Олі, а у Вови – 17-4=13.
- Відповідь: 8 гусенят, 4 гусенят.
- Відповідь: 12 слив, 18 слив.
- Відповідь: 8 кг, 4 кг.
- Відповідь: 22 кілограми.
- Відповідь: 10 копійок, 5 копійок.
- Відповідь: 6троянд, 9 троянд, 13 троянд.
- Відповідь: 20 кілограм, 15 кілограм, 32 кілограми.
- 22-2=20(шт.) – було б олівців у двох коробках, якби в них олівців було порівну. 20:2=10 (шт.) – олівців було б у кожній з двох коробок, якби в них олівців було порівну; або у тій коробці, де олівців менше. 10+2=12 (шт.) – олівців у першій коробці.
- 6+9=15(п.) – стільки персиків взяли з двох кошиків.
75-15=60 (п.) – всього в двох кошиках, коли в них стало яблук порівну.
60:2= 30 (п.) – стало в кожному кошику.
30+6=36 (п.) – було першому кошику.
30+9=39 (п.) – було в другому кошику.
Вікові зміни
- 12 років
- 17 років
- 14 років
- 16 років
- Через 12 років
- 24 роки
- 2 роки, 14 років
- На 5 років
- 11 рокiв
- Зима. Так
- Старшiй 9 років, Наташi 8років, Танi 8років.
- 10 годин
Часові залежності
- Сьогодні
- П’ятниця
- Неділя
- Ні, вона відпочивала 9 днів
- а) ранок, день, вечір, нiч ( доба )
б) весна, лiто, осiнь, зима ( пори року )
в) вересень, жовтень, листопад ( осiнь )
г) доба, тиждень, мiсяць, квартал ( мiри часу )
Геометричні задачі
- Відповідь: 7.
- Відповідь: 5.
- Відповідь: 25 метрів.
- Трикутників – 4, кружечків – 5, овалів – 6.
- Квадратів – 1, кружечків – 8, прямокутників – 2, трикутників – 4.
- Трикутників – 7, квадратів – 1, кружечків – 4.
7. Відповідь:

8. Відповідь:

9. Відповідь:
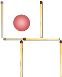
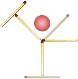
10. Відповідь:
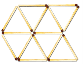
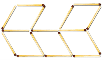
11. Відповідь:
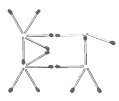
12. Відповідь:
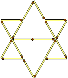
13. Відповідь:

14. Відповідь:

Позиційні задачі
- Прямокутник, трикутник.
- Трикутник, круг.
- Жовтий, червоний, зелений, синій.
- Трикутник, квадрат, коло, прямокутник.
- Овал, трикутник, квадрат, шестикутник.
- Овал, чотирикутник, трикутник, п’ятикутник.
Задачі на вилучення
- Відповідь:
|
|
Мишка |
Жабка |
Ведмідь |
Кабан |
|
Оля |
- |
+ |
|
|
|
Павлик |
- |
- |
- |
+ |
|
Марійка |
+ |
- |
|
|
|
Сергійко |
- |
- |
+ |
|
- Відповідь:
|
"Альбатрос" |
1 |
2 |
3 |
4 |
|
"Бригантина" |
1 |
2 |
3 |
4 |
|
"Вихор" |
1 |
2 |
3 |
4 |
|
"Глобус" |
1 |
2 |
3 |
4 |
3. Відповідь:
|
|
золота |
срібна |
бронзова |
|
Галинка |
|
|
- |
|
Жанна |
- |
+ |
- |
|
Наталка |
|
- |
|
4. Відповідь: Іван — у білій сорочці, Василь — у блакитній, Гліб — у зеленій, Микола - у червоній.
Логічні задачі
- Відповідь: 4.
- Відповідь: порівну.
- Відповідь: 2, 4, 6.
- Відповідь: 3.
- Відповідь: 3.
- Відповідь: 5 зайців, 20 лап.
- Відповідь: 2 + 2 + 1 = 5 оченят.
- Кіт і півень можуть прожити разом найбільше 3 роки – стільки, скільки живе півень
- Відповідь: 10.
- Відповідь: 17.
- Відповідь:
Позначимо кількість горіхів у Андрія –А, у Бориса – Б, у Володі – В. Тоді умову задачі можна записати трьома рівностями:
А + Б = 11
А + В = 12
Б + В = 13
А + Б + А + В +Б + В = 2А +2Б + 2В = 36
А + Б + В = 36 : 2 = 18
Із рівності 1 і 2 видно, що у Вови на один горіх більше, ніж у Борі: 12-11=1 (горіх). Оскільки у Вови і Бориса разом 13 горіхів, то можна дізнатися, скільки у них було б горіхів, якби у Вови було стільки ж горіхів, скільки у Бориса: 13 – 1 = 12 (горіхів). Тоді у Вови 6 + 1 = 7 (горіхів), а у Андрія 11 – 6 5 (горіхів), а у всіх разом 5 + 6 +7 = 18 (горіхів).
- Відповідь: усього 3 чоловіки – дід, батько, син.
- Відповідь: 12 яєць.
- Відповідь: Червона Шапочка несла 5 пиріжків із грибами.
- Відповідь: жодного, страуси не літають.
- Відповідь: 2 кілограми.
- Відповідь: Слід пригадати, що у жука 6 лап, а у павука – 8.У коробці було 5 жуків і 3 павуки.
- Відповідь: усіх семеро: чотири брати і 3 сестри. У кожного брата три брати і три сестри; у кожної сестри 4 брати і 2 сестри.
- Відповідь:1 пара.
- Відповідь: по одному. Два батька і два сини – це дід, батько і син)
- Міркування. За 16 днів. За кожні з перших 15діб мурашка піднімалася на 1 м. Отже, за 15 діб вона піднялася вгору на 15 м. А за 16-й день мурашка підніметься ще на 5 м і досягне вершини.
- Міркування. 15 бочок можна подати як 6 бочок + 6 бочок + 3бочки. : бочок уміщують 28 відер води. Тоді 3 бочки вміщують 14 відер води. Отже, 15 бочок уміщують 70 відер води.
- Міркування. Складемо шматок шовку пополам (8 м : 2 = 4м). Кожна частина буде по 4 м. А тепер одну з частин складемо ще на пополам (4 м: 2 = 2 м) і відріжемо її. 4 м + 4 м – 2 м = 6 м
- Відповідь: 7.
- Відповідь:
![]()

![]()
- Відповідь: 1 триколісний та 2 двоколісних.
- Відповідь: 2 поросят і 3 курей.
- Відповідь:

![]()
![]()
![]()
![]()
![]()
![]()
-



 Відповідь:
Відповідь:
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
- Відповідь:
![]()
![]()
- Розв’язання:
а) Чоловік перевозить козу.
б) Чоловік повертається один.
в) Чоловік перевозить вовка.
г) Чоловік повертається з козою.
д) Чоловік залишає козу і перевозить капусту.
е) Чоловік повертається один.
ж) Чоловік перевозить козу.
- Відповідь: 6.
- Відповідь: 60 страусів.
- Відповідь: Риба-пила.
- Відповідь: 32 шкарпетки.
- Відповідь: 9.
- Відповідь: 8 пампушок.
Міркуємо так: оскільки 2 пампушки – половина того, що було до того, як першу половину з’їв Малюк, отже до того, як Малюк узяв пампушки, їх було 4. Але 4 – друга половина від того, що було, першу ж з’їв Карлсон. Але якщо половина – 4, то ціле – 4 + 4 = 8 (пампушок).
- Міркування: за добу слимак просувається по стіні на 1 метр вгору (2 – 1). На кінець 8-ї доби він був на висоті 8 метрів. Увечері дев’ятого дня слимак піднявся на стіну. Це сталося у вівторок.
- Відповідь: 4 галки, 3 палки.
Для того щоб із цією задачею розібрались учні, малюємо: палки у вигляді відрізків, галок — у вигляді точок на них. Намалюємо одну палку. Виконаємо першу умову: посадимо на неї галку й одна галка має залишитись без палки. Малюємо точку окремо: Вийшло дві галки й одна палка.
Перевіряємо другу умову: якщо посадити на одну палку двох галок, усі палки будуть зайняті, тобто умови не виконані. Отже, палок більше ніж одна. Малюємо дві палки. Тоді галок має бути три. Якби вони сідали на ці дві палки по дві, то не залишилося б вільної палки (одна палка була б, дійсно, тільки з однією галкою):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
І нарешті, якщо намалювати три палки й чотири галки, то все вийде.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Відповідь: 7 олівців, 4 олівці.
- Відповідь: 5 корабликів, 3 кораблики, 8 корабликів.)
Комбінаторні задачі:
- 1) Іваненко, Сидоренко, Коноплянко;
2) Іваненко, Коноплянко, Сидоренко,;
3) Сидоренко, Іваненко, Коноплянко;
4) Сидоренко, Коноплянко, Іваненко;
5) Коноплянко, Іваненко, Сидоренко;
6) Коноплянко, Сидоренко, Іваненко.
2. Відповідь:
яблуко / банан / груша
груша / яблуко / банан
груша / банан / яблуко
банан / яблуко / груша
банан / груша / яблуко
Всього: 6 комбінацій.
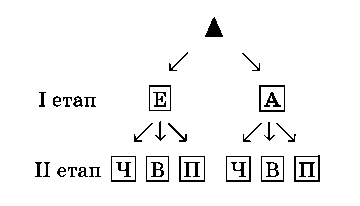
3. Розв'язання. Перший етап подорожі можна здійснити двома способами, а другий — трьома. Отже, всього існує 2 х 3 = 6 способів.
Розв'язання цієї задачі можна проілюструвати такою схемою (позначимо буквою Е пересування електропотягом, А — автобусом, Ч — човнами, В — велосипедами, П — пішки):
Усього існує 6 варіантів.
4. Усього існує 6 варіантів:
- книжка, альбом;
- книжка, ручка;
- книжка, гумка;
- альбом, ручка;
- альбом, гумка;
- ручка, гумка.
5. Усього існує 6 варіантів:
- Муха, Комар;
- Муха, Таракан;
- Муха, Жук;
- Блошка, Комар;
- Блошка, Таракан;
- Блошка, Жук.
6. Усього існує 4 варіанти:
1 дівчинка, 4 хлопчики;
2 дівчинки, 3 хлопчики;
3 дівчинки, 2 хлопчики;
4 дівчинки, 1 хлопчик.
Задачі на переливання:
1. Спробуємо дістати необхідну кількість води за допомогою переливання з 3 – літрової банки в 5 – літровий бідон. Наллємо двічі 3 літри води в 5- літровий бідон, у 3 – літровій банці залишиться 1 л води. Звільнивши бідон від води, вливаємо в нього1 л води і потім додаємо ще 3 л.
Спосіб 2.Спробуємо дістати необхідну кількість води за допомогою переливання з 5 – літрового бідона в 3 – літрову банку.
|
3 л |
0 |
3 |
0 |
2 |
2 |
3 |
|
5 л |
5 |
2 |
2 |
0 |
5 |
4 |
2. Нехай шукані 5 л води в результаті переливань опиняться у 7 – літровому бідоні. Необхідно заповнити 10 – літровий бідон, спустошуючи послідовно 3 – літровий і 7 – літровий бідони.
|
10 л |
7 л |
3 л |
|
5 |
5 |
3 |
|
2 |
5 |
3 |
|
2 |
5 + 2 = 7 |
3- 2 = 1 |
|
2 + 7 = 9 |
7 – 7 = 0 |
1 |
|
9 |
0 + 1 = 1 |
1 – 1 = 0 |
3. Розв’язання
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Розв’язання
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Наповнити 7-літрове відро, перелити з нього частину води у 3-літрову банку. У відрі залишиться 7-3=4 (л). Решту води з відра(4 л) перелити у каструлю. Тепер у каструлі не вистачає 5-4=1(л) води. Щоб отримати 1 л, ми виливаємо воду у колодязь із 3-літрової банки і знову наповнюємо 7-літрове відро. З відра переливаємо воду у 3-літрову банку, у відрі залишається 4 л води. З банки виливаємо воду у колодязь і з відра переливаємо в банку. тому у відрі залишається 4-3=1 л води. Цей 1 л ми доливаємо у каструлю: 4л+1л=5л.
Література:
1. Сухарева Л.С. Предметні тижні з математики в початковій школі. –
Видавництво «Ранок», 2010 рік, – 144 с.
2. ІвановаГ.Ж. Олімпіадні завдання з основних дисциплін. Вид. група «Основа», 2010, – 208 с.
3. Будна Н.О., Романишин І.Я., Тучапська Г.В. Предметні олімпіади. – Тернопіль: Навчальна книга – Богдан, 2005. – 32 с.
4. Микитинська М.І., Мацько Н.Д. Математичні ігри в 1-3 класах. – Київ «Радянська школа», 1980. – 128 с.
5. Беденко М.В. Математика – це справді цікаво. – Тернопіль: Навчальна книга – Богдан, 1999. – 96 с.
6. Баєва І.Ф., Руденко В.М., Мудрик О.І. Уроки розвитку логічного мислення у початкових класах. – Кам’янець-Подільський: Абетка, 2001. – 80 с.
7. Лісневич Т.Г. Цікаві задачі. Посібник для учнів початкових класів. – Тернопіль: Мандрівець, 1997. – 48 с.
8. Фадєєва Т. О. Методика розв’язування нестандартних задач з математики в початкових класах. – Кіровоград: РВЦ КДПУ, 2002. – 39 с.
9. Нестандартні задачі з математики. 1-4 класи / Упоряд. Н. В. Курганова - Х.: Вид-во «Ранок», 2010. –192 с. – (Навчаємо молодших школярів).
10. Гребенькова Л.О. Зимові вправи для другокласників. Робочий зошит для учнів 2 класу. – Х.: Вид-во «Ранок», 2013. – 64с.
11. Гриценко Н.І., Пильник Л.П., Немеш Л.В. Логіка. Нестандартні задачі. Робочий зошит. 2 клас. – Тернопіль: Навчальна книга – Богдан, 2011. – 80 с.
12. Фадєєва Т. Технологія складання нестандартних задач з математики. – Журнал «Початкова школа» №1 2009 р. – с.23-28.
13. Дудко Л., Московченко В. Система задач з логічним навантаженням для учнів 3-4 класів. – Журнал «Початкова школа» №9 2005 р. – с.31-33.
14. Корчевська О. Робота над завданнями підвищеної складності з математики в початкових класах. – Тернопіль: Підручники і посібники, 2001. – 112 с.
15. Карнаух П.М. Цікаві завдання з математики. 2 клас: Навчальний посібник. – Тернорпіль: Навчальна книга – Богдан, 2003. – 40 с.
16. Сухарева Л.С. Задачі із сірниками. – Х.: Вид. група «Основа», 2007. – 80 с.
17. Сухарева Л.С. Математичний гурток у початковій школі. – Х.: Вид. група «Основа», 2007. – 112 с.
18. Сухарева Л. С. Задачі на переливання, зважування, перекладання. — X., 2007.— 48 с.— (Серія «Математичний гурток в початковій школі»).

1

про публікацію авторської розробки
Додати розробку

-

Мосийчук Альона
17.12.2023 в 21:29
дяккую! Дуже класні задачі!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Щиренко Ірина Михайлівна
21.06.2023 в 17:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лебедева Юля
24.05.2023 в 12:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Суріна Сніжана Сергіївна
18.06.2022 в 16:00
Величезне дякую! Дуже корисно)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лобач Светлана
23.02.2022 в 21:29
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ємельянова Ганна Іванівна
18.01.2022 в 22:56
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Фукс Юлія Феліксівна
02.08.2021 в 18:18
Дякую за чудовий посібник
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ярошенко Світлана Іванівна
27.01.2021 в 11:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кравцова Ганна Миколаївна
20.12.2020 в 18:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жаркова Ірина Іванівна
21.01.2019 в 20:59
Дуже корисний посібник!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 7 відгуків