Нестандартний урок-подорож із застосуванням активних методів навчання та елементів самоконтролю (на прикладі теми: «Додавання і віднімання десяткових дробів»)

Нестандартний урок-подорож із застосуванням активних методів навчання та елементів самоконтролю (на прикладі теми: «Додавання і віднімання десяткових дробів»)

Мета. Формувати вміння та навички учнів додавати і віднімати десяткові дроби, розвивати навички обчислювальної техніки, усної лічби; продовжувати розвивати уміння працювати самостійно і в парі з товаришем (партнерство); розвивати навички самоконтролю, уважність, кмітливість, навички логічного мислення; виховувати активність, наполегливість, працьовитість, акуратність, самокритичність.

Тип уроку. Урок формування навичок і вмінь. Урок-подорож.

Активні методи навчання. Метод мозкового штурму (ММШ), метод занурення. Індивідуальна робота з додатковою літературою (4 учні).

Засоби навчання. Карта подорожі по місту «Десяткові дроби», кодоскоп, картки із завданнями, гра «Танграм», навчальна література: підручник математики, «Збірник задач і вправ для 5-6 класів» (автори: А.Г. Мерзляк та інші), конкурсні завдання «Кенгуру», кольорова крейда.

Девіз. «Обчислюй та міркуй раціонально».

Хід уроку

І. Організаційний момент.

Учитель: розпочинаючи роботу на уроці, я хочу запитати: чи є запитання по домашньому завданню? Всі виконали завдання? Якщо запитань немає, то продовжимо роботу.

Сьогодні урок у нас буде незвичайний. Проведемо його у вигляді подорожі у велике місто «Десяткові дроби». Нас з вами чекають цікаві зупинки. Хочу зауважити, що у нашій роботі нам допоможе вислів І. Хіксона «Якщо відразу немає успіху, то спробуйте ще і ще». Це мало б застерегти нас від можливого розчарування від невдач. Ми продовжуємо вивчати додавання і віднімання десяткових дробів, розв’язувати з їх використанням багато цікавих вправ. І тому, обчислюйте, міркуйте, причому раціонально, пам’ятаючи, що «швидкість потрібна, а поквапливість – шкідлива», як говорив великий російський полководець О.В. Суворов.

Давайте помандруємо всі разом до чудового міста, де багато-багато квітів пізнання, дерев, цифр і будинків у формі геометричних фігур. А для того, щоб помилуватися цією дивовижною красою природи та споруд, вирушимо пішки. Ну то що ж, вирушаємо?

ІІ. Актуалізація опорних знань.

Учитель перевіряє повне розуміння використання алгоритму додавання та віднімання десяткових дробів, активізує розумову діяльність (ММШ).

Учитель: Оскільки місто нам не дуже знайоме, у розвідку спершу підуть 6 учнів, які оглянуть його та повідомлять про його найцікавіші куточки (шести учням роздають завдання по картках).

Учитель. Поки розвідка працює, давайте ознайомимось із зупинками, які чекають нас на даному маршруті:

Зупинка 1 – «Теоретична», зупинка 2 – «Історична», зупинка 3 – «Уважність», зупинка 4 – «Практична», зупинка 5 – «Творча», зупинка 6 – «Підсумкова». (Учні допомагають перевіряти виконані на дошці завдання, кольоровою крейдою виставляють оцінки).

Зупинка 1. «Теоретична» (фронтальна бесіда)

«Запитання від Незнайки»:

1. Які дроби ви знаєте?
2. Що таке десятковий дріб?
3. Як відрізнити десятковий дріб від звичайного?
4. З яких частин складається десятковий дріб?
5. За яким принципом записують десяткові дроби?
6. Сформулюйте правило порівняння десяткових дробів.
7. Сформулюйте правило округлення десяткових дробів.
8. Сформулюйте алгоритм додавання і віднімання десяткових дробів.
9. Які закони додавання ви знаєте?
10. Записати буквені вирази цих законів.

Учитель звертає увагу учнів на унаочнення усних вправ. – Прочитайте десяткові дроби:

11,4; 888,8; 0,9; 21,87; 2,80; 0,55; 1,579; 326,703; 145,004; 203,6; 0,002; 0,20506.

• Порівняйте числа:

85,09 і 67,99; 0,5 і 0,724; 0,0025 і 0,00247; 55,7 і 55,700; 7,6431 і 7,6429.

• Округліть число 2,0724 до:

а) цілих; б) десятих; в) сотих; г) тисячних.

Учитель оцінює чотирьох учнів, які відповідали на теоретичні і практичні завдання, враховуючи виконання домашнього завдання. Два учні на сусідніх дошках відновлюють ланцюжок розрахунків:

-

-

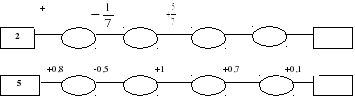
Зупинка 2. «Історична»

Готуючись до цього уроку, попередньо учням було запропоновано вдома дібрати цікаву інформацію з історії десяткових дробів [10]. На цій зупинці вони розповідають про мандрівку в минуле.

Учень 1. Десяткові дроби, як і звичайні, виникли на основі практичної потреби в торгівлі, будівництві тощо. Розвиток науки, техніки, промисловості, розширення торговельних відносин вимагали дедалі складніших обчислень. Тому постало питання про спрощення дій з дробами. Так виникло поняття десяткового дробу.

Учень 2. В Азії дроби застосовували ще до нашої ери (ІІ ст. до н.е.). У ХV столітті аль-Каші, астроном і математик із Самарканда, у своїй праці «Ключ до арифметики» (1427 р.)систематизував і значно розвинув знання про десяткові дроби, а самі дроби зображав так: 5843257 (риска ставилася між цілою і дробовою частиною).

Учень 3. У 1585 році нідерландський учений Сімон Стевін опублікував свою працю «Десятина» про десяткові дроби (те, що десяткові дроби відкрив аль-Каші, європейці ще не знали). Але запис, який запропонував Стевін, був незручним. Наприклад, десятковий дріб 35,912 він записував 35 9 1 2. Кому, як знак, що розділяє цілу й дробову частини числа, запропонував математик з Шотландії Джон Непер (1550-1617). Його математичні роботи були направлені на спрощення та впорядкування записів в арифметиці, алгебрі та тригонометрії. Але ще раніше кому застосовував німецький вчений Йоган Кеплер (1571-1630).

Учень 4. У Росії вперше вчення про десяткові дроби виклав Л.Магницький (1669-1739) у своїй «Арифметиці» - першому російському підручнику з математики (1703 р.). Арифметичні дії з десятковими дробами набагато простіші, ніж зі звичайними, і тому вони застосовуються частіше.

Учитель. Ось так виглядає минуле дробів. До речі, цікаве і влучне «арифметичне» порівняння належить російському письменнику і філософу Льву Толстому. Він казав, що людина подібна до дробу, знаменником якого є те, що людина про себе думає а чисельником – те, що людина являє собою. Чим більшої думки про себе людина, тим більший знаменник, а отже , менший дріб. Тож напрошується висновок пне пишайся собою, а працюй, вдосконалюй себе, гартуй розум і волю, щоб про твої вчинки кращої думки були інші.

Зупинка 3. «Кмітливість»

Девіз: «Думай швидше»

1. Який знак слід поставити між числами 4 і 5, щоб вийшло число, більше за 4 і менше за 5? (Кому).
2. Які числа не змінюються, якщо їх перевернути? (8; 88; 96; 69).
3. Що довше: пряма чи промінь? (Відповісти неможна).
4. Який найдавніший прилад для лічби? (Пальці).
5. З цифр 3 і 0 складіть частку. (0:3).
6. Від колоди довжиною 7 метрів щохвилини відпилюють по одному метру. За скільки хвилин розпилять всю колоду? (6 хвилин).
7. Що спільне у рівняння і дерева? (Корінь).
8. У числі 10,00830750 закреслити три нулі так, щоб воно було найбільшим. (10,8375).

Зупинка 4. «Практична»

Колективно розв’язуємо такі завдання:

№ 407 (1, 3, 5, 10). Відповідь: 1) 10,5; 3) 10,35; 5) 20,2; 10) 11,7.

№ 411 (2, 4, 6, 8, 9). Відповідь: 2) 5,5; 4) 17,82; 6) 18,68; 8) 42, 549; 9) 3,622.

Хто швидше? (З кожного ряду до дошки виходять по одному учню. Решта учнів розв’язують те рівняння, яке розв’язує учень з їхнього ряду.)

№ 413 (1, 4, 6). Відповідь: 1) 4,17; 4) 2,272; 6) 56.

Індивідуальна робота. (Учні по черзі, коментуючи, розв’язують задачі з повним обґрунтуванням).

Задача № 409 (2).

1. Яка площа другої кімнати Бабусі Ягусі?

17,6+5,9=23,5 (м²).

1. Яка площа двох кімнат Бабусі Ягусі?

17,6+23,5=41,1 (м²). Відповідь: 41,1 м²

Задача № 414 (2).

1. Яка швидкість моторного човна за течією річки?

16,4+1,8=18,2 (км/год).

1. Яка швидкість моторного човна проти течії річки?

16,4-1,8=14,6 (км/год).

Відповідь: 18,2 км/год; 14,6 км/год.

Далі вчитель ділить клас на групи, по 4 учні у кожній; вибирає старшого групи – доповідача.

Група 1. Задача № 417 (1). Відповідь: Барвінок зібрав на 0,16 кг грибів більше, ніж Івасик-Телесик.

Група 2. Задача № 417 (3). Відповідь: Барон Мюнхаузен за перші три хвилини польоту пролетів 819,6 км.

Група 3. Задача № 418 (2). Відповідь: Площа третьої ділянки, яку придбав пан Матроскін, дорівнює 177,76 га.

Група 4. Задача № 419 (2). Відповідь: Периметр трикутника дорівнює 38,4 дм.

Група 5. Задача № 418 (1). Відповідь: Наф-Наф зібрав 841,49 кг бананів.

Група 6. Задача № 409 (1). Відповідь: Дядько Скрудж отримав за грудень і січень 894,12 тисяч доларів прибутку.

Самостійна робота

Варіант 1. № 420 (1). Відповідь: а=32,9; b=5,868; х=4,132.

Варіант 2. № 420 (2). Відповідь: а=25,32; х=48,803; у=8,603.

Перші п’ять зошитів учитель бере на перевірку. Інші обмінюються зошитами і перевіряють роботи (взаємоконтроль).

Самоконтроль: Відповіді вчитель проектує відповіді на дошку за допомогою кодоскопу й пропонує тим учням, які припустили помилки, самостійно виправити їх, орієнтуючись на правильний результат.

Зупинка 5. «Творча» (гра у «Танграм»)

Метод занурення. Робота в парах. (На кожну парту вчитель роздає розрізані геометричні фігури з кольорового паперу. Кожна пара повинна скласти з цих фігур: будиночок, зайчика, вовка, рибу, журавля…). Учні складають фігури на картоні і демонструють зроблене вчителю.

Танграм

«Риба»

«Будиночок»

Учитель. Отож, бачимо, результати відразу помітні. Багатьом з вас ці завдання вдалося виконати так чудово, наче б то робили професійний художник чи архітектор (див. рисунок «Танграм»). Перший, другий та третій ряди знаходять периметр фігур № 1, № 6 і № 7 відповідно.

У цей час чотири учні на дошці працюють із наступними завданнями, записаними на картках.

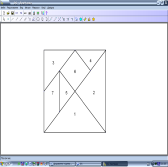
Завдання 1. Скільки відрізків на малюнку? Випишіть їх.

Відповідь: 6 відрізків.

Завдання 2. Скільки квадратів на малюнку?

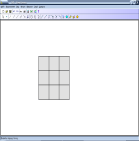
Відповідь: 14 квадратів.

Завдання 3. Скільки кутів зображено на малюнку? Випишіть їх.

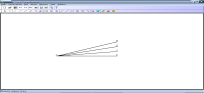
Відповідь: 6 кутів.

Завдання 4. Скільки трикутників на малюнку? Випишіть їх.

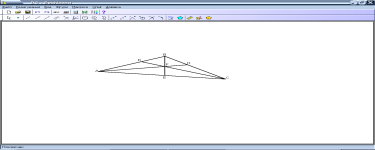
Відповідь: 16 трикутників.

Самоконтроль: За допомогою кодоскопа на дошку проектуються малюнки та правильні відповіді до завдань, учням, які припустили помилки пропонується самотужки знайти їх і показати на малюнках всі шукані фігури.

Учитель: З розглянутих вправ неважко зрозуміти, що треба вміти не просто дивитися, а дивитись і бачити. Отож, наші майбутні програмісти чудово впоралися із завданням. (Вчитель оцінює учнів, які добре працювали на даній зупинці, а також тих, хто зумів знайти свої помилки та самостійно виправити їх).

Зупинка 6. «Підсумкова»

IV. Завдання додому.

1. Скласти кросворд.
2. № 1008 (а, б, е), № 1011 (а, б, е), № 1015 [34].

V. Підсумок уроку.

Учитель. Наша подорож завершена. Чи сподобалась вам ця своєрідна мандрівка у місто десяткових дробів? Яка зупинка вам найбільше запам’яталась? Яких учнів сьогодні ми можемо відзначити за вміння допомагати іншим? За вміння своєчасно знайти та виправити помилку?

Урок закінчено.

Отже, за планом цього уроку чітко простежуються керовані вчителем контрольні дії учнів (як із взаємоконтролю, так самоконтролю), тому крім дидактичного та пізнавального навантаження даний урок виконує функції розвитку навичок самоконтролю та рефлексивних дій учнів. Інші приклади нестандартних уроків контролю наводяться у додатках А, Б.