Ньютонівські та неньютонівські рідини

Про матеріал

Наукова робота за темою" Ньютонівські та неньютонівські рідини."Матеріали можна використати для підготовки до уроку або додаткових занять у класах з поглибленим вивченням фізики.

Перегляд файлу

Методичний кабінет КЗШ І-ІІІ ступенів №60

Виконав:

учень 11-А класу

КЗШ І-ІІІ ступенів №60

Гузман Станіслав

Керівник: Коновалова С.Є.

Вчитель вищої категорії

Кривий Ріг

2014 рік

Зміст

ВСТУП

І. ВИВЧЕННЯ НЬЮТОНІВСЬКИХ ТА НЕНЬЮТОНІВСЬКИХ РІДИН

1.1 Технічна діяльність Ісаака Ньютона

1.2 Загальна характеристика та класифікація рідин

1.3 Трясовина - як приклад природної бінгамівської рідини

ІІ. ЕКСПЕРИМЕНТАЛЬНА ЧАСТИНА

2.1 В’язкість, як основна характеристика рідин

2.2 Способи вимірювання в’язкості

2.3 Вимірювання динамічної та кінематичної в’язкості

Висновки

Список використаної літератури

ВСТУП

Рідкі тіла класифікують на ньютонівські і неньютонівські рідини. Ньютонівські рідини - це системи, в'язкість яких не залежить від напруги зсуву і є постійною величиною відповідно до закону Ньютона. Перебіг неньютонівських рідин не підпорядковується закону Ньютона, їх в'язкість залежить від напруги зсуву. Неньютонівські рідини поділяються на стаціонарні, реологічні властивості яких не змінюються в часі, і нестаціонарні, для яких ці характеристики залежать від часу. Неньютонівські стаціонарні рідини поділяються на псевдопластичні та ділатантні.

Псевдопластичні рідини не виявляють меж текучості, і крива течії в них показує, що відношення напруження зсуву і градієнта швидкості, яке в даному випадку характеризує уявну, або ефективну, в’язкість, поступово знижується зі зростанням градієнта швидкості.

Прикладом псевдопластичних рідин є: розчини каучука, розчини мастила, розчини полімерів, фармацевтичні розчини, різні харчові продукти, біологічні рідини тощо.

Дилатантні рідини -стаціонарно реологічно аномальна рідина, в'язкість якої із зростанням градієнту швидкості зростає.Прикладом дилатантних рідинє: висококонцентровані водні суспензії порошків двоокису титану, заліза, слюди, системи пісок/вода, гідрозоль крохмалю, солодкі суміші, водні розчини гуміарабіку та ін.

Бінгамовська рідина - в статичних умовах веде себе як твердий матеріал, а при силовому впливі починає текти. Прикладами бінгамовської рідини можуть бути: шлами, бурові розчини, масляні фарби, стічні води, різні емульсії та інші рідини

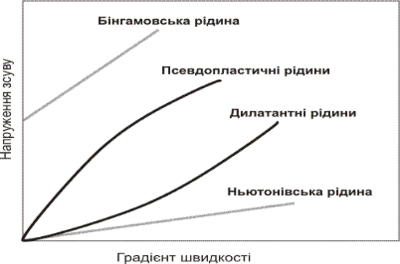
Проблема дослідження течій бінгамовскіх середовищ в каналах і порожнинах із змінними формами вібруючих стінок з'явилася безпосередньо з потреб практики , з метою розробки нового покоління харчових технологічних машин, що працюють на вібраційно - хвильових принципах. Принципова відмінність таких машин від відомих полягає в наявності у них м'якого деформованого робочого органу тимчасово в низькочастотне хвильове і високочастотне вібраційне руху. Робочий орган 1 при цьому деформується і набуває деяку непостійну з часом форму. З таким незвичайним робочим органом безпосередньо і взаємодіють оброблювані бінгамівскі харчові середовища , до яких відносяться ,

наприклад , різні м'ясні і рибні фарші , сиркові - сирні маси і багато іншого.

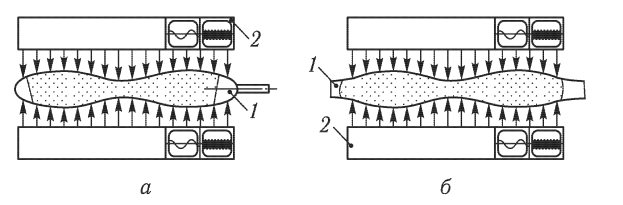
Течія більшості неньютонівських матеріалів починається за найменших значень напруження зсуву, і їх криві течії мають лінійну залежність між напруженням і швидкістю зсуву тільки за дуже малих (в’язкість η=0 ) і дуже великих (в’язкість η=∞ ) значень швидкості. Аномалія в’язкості пов’язана зі структурою рідини та її зміною під час течії. За малих швидкостей зсуву структура руйнується і повністю відновлюється, при цьому рідина має найбільшу в’язкість; із збільшенням швидкості зсуву руйнування структури починає переважати над відновленням, в’язкість різко зменшується; за великих швидкостей течії структура повністю руйнується, рідина має найменшу (ньютонівську) в’язкість.

В’язкість рідин також визначається для проведення діагностики захворювань у медицині. Як відомо кров, плазма і сироватка крові є прикладом бінгамівських рідин, а показник в’язкості крові у здорової та хворої людини мають різні значення. Отже з метою діагностики різних видів захворювань проводять аналіз в’язкості плазми і сироватки крові.

Саме тому ми вважаємо проведену експериментальну роботу актуальною, бо вимірювання в’язкості речовин має важливе значення не тільки у техніці, харчовій промисловості, але й у медицині.

Мета дослідження: вивчити характеристику та властивості ньютонівських та неньютонівських рідин. Розрахувати динамічну та кінематичну в’язкість деяких речовин методом Стокса.

Предмет дослідження: різні види ньютонівських та неньютонівських рідин.

О’бєкт дослідження: динамічна та кінематична в’язкість рідин

І. ВИВЧЕННЯ НЬЮТОНІВСЬКИХ ТА НЕНЬЮТОНІВСЬКИХ РІДИН

1.1 Технічна діяльність Ісаака Ньютона

В історії фізики не була події більш видатного, ніж створення механіки Ньютона. Майже 250 років фізики, астрономи й інженери всього миру опиралися у своїй роботі на закони Ньютона, і лише на початку ХХ століття інший найбільший фізик - Альберт Ейнштейн відкрив нові закони руху. Але теорія Ейнштейна не суперечить механіці Ньютона, а тільки доповнює й уточнює її. У практиці, починючи від виготовлення дитячих іграшок і до конструювання гігантських космічних кораблів, механіка Ньютона завжди буде зберігати своє значення.

Досягнення Ньютона в механіці були підготовлені роботами Галілео Галілея, Х. Гюйгенса й інших учених. У роботі «Математичні початки натуральної філософії» він звів усі факти, відомі до нього й усі знайдені їм самим відомості про рух і сили в одну дедуктивну систему. Установивши кілька основних законів механіки (закон інерції, закон незалежної дії сил, закон про рівність дії й протидії), Ньютон вивів з них усі інші теореми механіки.

Ньютон відкрив закон всесвітнього тяжіння, указав на ту загальну силу, яка є першопричиною таких різноманітних явищ, як падіння тіл, обертання Місяця навколо Землі й планет навколо Сонця, рух комет, припливи й відливи і т.д. Звичайно, і в області небесної механіки в Ньютона були попередники (Борели, Р. Гук і інші), але йому вдалося знайти саме доконане формулювання закону всесвітнього тяжіння. Він обґрунтував справедливість цього закону всіма відомими в той час астрономічними фактами й обчислив на основі його траєкторії тіл, які рухаються в різних умовах у поле тяжіння.

Крім того, Ньютон досліджував рух тіл у середовищі, що виявляє опір. Він вивчав теплові властивості різних речовин.

Йому належать фундаментальні відкриття в оптиці, зокрема він з'ясував причину розсіювання світла, показав, що біле світло розкладається на кольори веселки внаслідок різного переломлення променів різних кольорів при проходженні через призму, і заклав основи правильної теорії кольорів.

«Математичні початки натуральної філософії» (1687) Ньютона містять розвинену теорію конічних перетинів, необхідну для дослідження руху планет і комет. Ньютон сформулював основні закони механіки й запропонував теорію всесвітнього тяжіння, яка визначає як падіння яблука з дерева, так і рух планет навколо світил. Ньютон став головним героєм епохи Просвітництва, що настала в 17 столітті.

1.2 Загальна характеристика та класифікація рідин

Псевдопластичні рідини не виявляють меж тікучості, і крива течії в них показує, що відношення напруження зсуву і градієнта швидкості, яке в даному випадку характеризує уявну, або ефективну, в’язкість, поступово знижується зі зростанням градієнта швидкості.

Дилатантні рідини - стаціонарно реологічно аномальна рідина, в'язкість якої із зростанням градієнту швидкості зростає. Прикладом дилатантних рідин є: висококонцентровані водні суспензії порошків двоокису титану, заліза, слюди, системи пісок/вода, гідрозоль крохмалю, солодкі суміші, водні розчини гуміарабіку та ін.

Бінгамівська рідина: модель Бінгама схожа до моделі сухого тертя. В статичних умовах ведуть себе як тверді матеріали, але при силовому впливі починають текти. Мінімальне зусилля, що необхідно прикласти до системи, щоб вона почала текти називається напруженням зсуву .

В'язкість деяких рідин, при сталих умовах навколишнього середовища і швидкості зсуву, змінюється з часом. Якщо в'язкість рідини з часом зменшується, то рідину називають тиксотропною, а якщо, навпаки, збільшується, то — реопексною. Обидві поведінки можуть спостерігатися як разом з описаними вище типами плину рідин, так і при певних градієнтах швидкостей. Часовий інтервал може сильно змінюватись для різних речовин: деякі матеріали досягають сталого значення в'язкості за декілька секунд, інші – за декілька днів. Реопексні матеріали зустрічаються досить рідко, на відміну від тиксотропних, до яких відносяться мастила, друкарські чорнила, фарби.

Рідина неньютонівська — модель рідини, що являє собою суцільне рідке тіло, для якого дотичні напруження внутрішнього тертя , спричиненого відносним проковзуванням (зсувом) шарів рідини описуються нелінійною залежністю від градієнта швидкості у напрямі, перпендикулярному до напрямку проковзування. На відміну від ньютонівських рідин, коли динамічний коефіцієнт в'язкості є константою при заданій температурі і тиску, особливість неньютонівських рідин полягає у залежності параметра в'язкості від градієнту швидкості. Як синонім до терміну «неньютонівська рідина» вживається, також, термін «аномальна рідина».

Класифікація неньютонівських рідин

Неньютонівські рідини в залежності від характеру течії та виду функціонального зв'язку, швидкості деформації та швидкості зсуву підрозділяють на три основних категорії:

- в'язкі середовища, у яких швидкість зсуву залежить від прикладання напруження зсуву (різні типи нафтопродуктів, консистентні мастила, будівельні розчини та інші дисперсні системи типу суспензій);

- середовища, реологічні характеристики яких залежать від часу (в таких рідинах швидкість зсуву визначає не лише величина дотичного напруження, але й тривалість дії);

- в'язко-пружні рідини, які мають властивості як рідини, так і твердого тіла та частково виявляють пружне відновлення форми після зняття напруження.

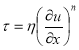τ- дотичне напруження внутрішнього тертя в рідині (Па)

-градіент швидкості у напрямі┴до напряму ссуву (с^-1)

- коефіцієнт пропорційності (Па∙с)

Класифікація рідин робиться за значенням показника n та часовою залежністю в'язких характеристик:

Ньютонівська рідина — лінійний закон (n = 1) ;

Степенева рідина — нелінійна, закон степеневий (n ≠ 1);

Псевдопластик — (n<1) , при малих швидкостях в'язкість значна, далі зменшується (фарби, емульсії, деякі суспензії);

Дилатантна рідина — (n>1), в'язкість зростає із збільшенням швидкості (глиняні суспензії, солодкі суміші, гідрозоль кукурудзяного крахмалю, системи пісок/вода);

Пластична рідина (бінгамівський пластик) — модель Бінгама схожа до моделі сухого тертя. В статичних умовах ведуть себе як тверді матеріали, але при силовому впливі починають текти. Мінімальне зусилля, що необхідно прикласти до системи, щоб вона почала текти називається напруженням зсуву ():

РЕОЛОГІЯ (грец. rheos — течія, потік + logos — слово, вчення) — розділ механіки, що вивчає закономірності деформації й плинність матеріальних систем під дією зовнішніх навантажень.

Реологічні властивості рідини при зсуві характеризуються її в’язкістю η (при ламінарному режимі течії). Ламінарною (шаруватою) називають таку течію рідини, при якій частинки рідини рухаються вздовж прямолінійних траєкторій, не перемішуючись; іншими словами, рідина може бути представлена у вигляді сукупності шарів, які при течії ковзають один відносно іншого (рис. 1).

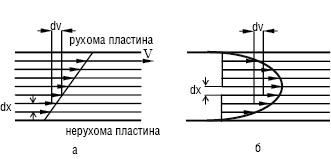
Рис. 1. Деформація рідини між двома пластинами (а) та у трубці (б)

При русі шарів рідини з різними швидкостями між ними виникають сили внутрішнього тертя Fтер, або сили в’язкості. Течія ідеально в’язких тіл (рідин) описується законом Ньютона:

(1)

де — модуль градієнта швидкості в напрямі х, перпендикулярному напряму руху її шарів; s — площа зіткнення шарів; η — коефіцієнт внутрішнього тертя, або динамічна в’язкість. Фізичний зміст динамічної в’язкості полягає в такому — вона чисельно дорівнює імпульсу, що переноситься від шару до шару в одиницю часу через одиничну площу при градієнті швидкості, рівному одиниці. В’язкість також можна визначити як силу, яку потрібно докласти до шарів рідини з площею s = 1, щоб створити градієнт швидкості, рівний одиниці. В СІ одиницею в’язкості є Паскаль-секунда [Па⋅с]. Якщо величина динамічної в’язкості характеризує опір рідини рухові її шарів під дією зовнішніх сил, то величина ν = 1/η характеризує рухливість рідини і називається плинністю (вона є зворотною в’язкості).

Виходячи з того, що напруження, яке викликає деформацію зсуву, визначається відношенням сили F до площі S, тобто P = F_тер/S, і враховуючи, що градієнт швидкості течії при зсуві дорівнює швидкості деформації , дійдемо до співвідношення: (2)

де γ´ — швидкість розвитку деформації (далі — швидкість деформації).

Рівняння (2) є також відображенням закону Ньютона, згідно з яким швидкість деформації пропорційна напруженню зсуву. При дослідженні реологічних властивостей найбільш наочним є графічне представлення результатів у вигляді реограм або кривих течії, які за звичаєм будують у координатах γ´ – P або η — P. Реологічні властивості ідеальних рідин однозначно характеризуються в’язкістю, і в цьому випадку графічна залежність у координатах γ´ – P є прямою, що проходить через початок координат (рис. 2а). В’язкість структурованих рідин, напр. багатоатомних спиртів, залежить від швидкості деформації (рис. 2б). Реологічні властивості таких систем характеризують за допомогою ефективної, або так званої уявної в’язкості η_еф = Р/ γ´.

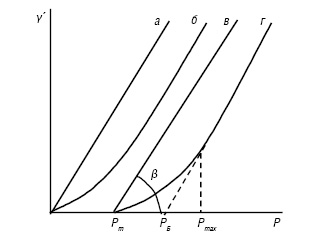
Рис. 2. Криві течії різних тіл

Рідини та гази здатні текти (деформуватися) під дією дуже малих зовнішніх навантажень доти, поки вони діють, але в’язкість газів значно менше в’язкості рідини. Так, в’язкість повітря при 20 ^оС становить 0,181·10^-4 Па·с, води — 1·10^–3 Па·с, гліцерину — 1499·10^–3 Па·с, а у твердих тіл в’язкість може сягати 10¹⁵–10²⁰ Па·с. Така значна відмінність в’язкості твердих тіл від газових та рідких систем зумовлена особливостями їх структури, завдяки чому навіть при значних напруженнях зсуву в твердих тілах розвиваються лише пружні деформації. Ф.М. Шведов, а пізніше Е. Бінгам, показали, що за певних умов у деяких твердоподібних тілах (пасти, глини) структура руйнується при досягненні напруження величини P_m, яка зветься межею плинності, і має місце пластична деформація (рис. 2в, г). Межею плинності називається мінімальне напруження зсуву, при досягненні якого починається течія. Так поводять себе ідеально-пластичні тіла. Реологічна поведінка тіл, що виявляють пружні та в’язкі властивості, підпорядковується рівнянню Бінгама:

P = P_m + η*γ´,(3)

де η* — пластична в’язкість, яка характеризує швидкість руйнування структури тіла. Пластична в’язкість може бути виражена з рівняння (3) як

η* = (P – P_m)/ γ´ = ctgβ, де β — кут, створений прямою в на рис. 2 та віссю абсцис.

За фізичним змістом пластична в’язкість відрізняється від ньютонівської в’язкості тим, що остання враховує всі види опору течії тіла, а пластична в’язкість, що є частиною ньютонівської, не враховує міцності структури, яка характеризується межею плинності.

Аналіз рівняння Бінгама показує, що при Р_m = 0 співвідношення (3) переходить в закон Ньютона, при Р > Р_m швидкість деформації зростає лінійно із збільшенням напруження (рис. 2в), а при Р < Р_m швидкість деформації дорівнює нулю. Для більшості структурованих систем залежність γ’ від Р нелінійна (рис. 2г). Це пояснюється тим, що при досягненні межі плинності структура руйнується поступово, у міру збільшення γ’. Можна виділити три критичні напруження зсуву: перша, або мінімальна межа плинності Р_m, відповідає початку течії (початку руйнування структури); далі межа плинності за Бінгамом, що відповідає відрізку на вісі абсцис, який відсікається продовженням лінійної ділянки кривої; третій відповідає максимальній межі плинності Р _max, при якій крива переходить у пряму лінію. Очевидно, що Р_max являє собою те напруження, при якому структура в рідині руйнується повністю. Зручність того або іншого рівняння не є єдиним і найважливішим критерієм при описі реологічної поведінки системи. Найбільш істотним є виявлення причин виникнення пружних, пластичних та інших властивостей, встановлення залежності параметрів, що характеризують структурно-механічні властивості систем від складу і структури середовища, яке деформується. Рішення цієї основної задачі пов’язане з вивченням фізико-хімічних закономірностей процесів структуроутворення.

Відповідно до реологічних властивостей тіла поділяють на рідиноподібні (межа тікучості дорівнює нулю) та твердоподібні (межа тікучості більша за нуль). Рідиноподібні тіла, у свою чергу, класифікують на ньютонівські і неньютонівські рідини. В’язкість ньютонівських рідин не залежить від напруження зсуву і є величиною постійною (напр. вода, спирти, ацетон, плазма крові). Тобто течія таких рідин підпорядковується рівнянню Ньютона (рівняння 2), згідно з яким швидкість деформації зростає лінійно із збільшенням напруження зсуву. Подібні рідини називають нормальними. Крива течії ньютонівської рідини наведена на рис. 2а. Неньютонівськими називаються рідини, в’язкість яких залежить від напруження зсуву, тобто є функцією швидкості деформації (напруження) в рівнянні Ньютона. Відповідно течія неньютонівських рідин не підпорядковується цьому рівнянню, а самі рідини називають аномальними. У цих випадках швидкість деформації нелінійно змінюється із збільшенням напруження зсуву (рис. 2б). Так поводять себе деякі розбавлені міцелярні розчини колоїдних ПАР, природні суспензії зі сферичними частинками, кров. Типові криві течії рідиноподібних тіл наведені також на рис. 3. Розподіл плинних матеріалів на ньютонівські і неньютонівські відображає їх поведінку тільки в сталому процесі безперервного деформування з певною швидкістю, причому, мається на увазі, що стан і властивості системи в часі не змінюються. Узагальненням закону Ньютона на випадок нелінійної залежності γ’ від Р є емпіричне рівняння Оствальда — Вейля

Р = k(γ’)ⁿ (4)

де k і n — сталі, що характеризують дану рідиноподібну систему.

Якщо n = 1, рідина є ньютонівською і параметр k збігається зі значенням ньютонівської в’язкості η (крива 1 на рис. 3).

При n > 1 швидкість деформації зі збільшенням напруження зсуву зростає швидше, ніж згідно з лінійним законом, відповідно ньютонівська в’язкість зростає із збільшенням швидкості деформації зсуву (крива 2 на рис. 3). Цей тип кривих належить до так званих дилатантних рідин. Дилатантна поведінка спостерігається в концентрованих агрегативно стійких суспензіях, де немає постійного контакту між частинками.

У випадку n < 1 ньютонівська в’язкість знижується із зростанням швидкості деформації зсуву, що характерно для псевдопластичних рідин (крива 3 на рис. 3). Суспензії з асиметричними частинками, розчини полімерів виявляють псевдопластичні властивості.

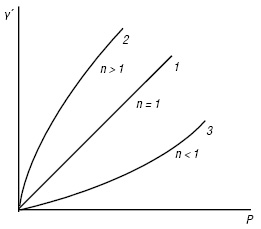
Рис. 3. Криві течії рідиноподібних тіл: 1– ньютонівські рідини; 2 — дилатантні рідини; 3 – псевдопластичні рідини

Структуровані системи внаслідок наявності сил взаємодії між їх частинками виявляють певною мірою властивості твердих тіл: здатність зберігати форму, певну міцність, еластичність. Але через малу міцність зв’язку між окремими елементами таких систем структура легко руйнується, а ці системи набувають здатності текти. Їх реологічна поведінка не підпорядковується закону Ньютона і може бути описана рівнянням Бінгама (рівняння 3). До таких систем відносять гелі, пасти, масляні фарби. Для них на відміну від типових твердоподібних тіл характерна низька межа тікучості. Типові криві течії твердоподібних тіл наведені на рис. 2 (в, г) та 4. Твердоподібні дисперсні системи поділяються на бінгамівські й небінгамівські. Їх поведінка описується загальним рівнянням

Р — Р_m = k (dγ / dt)n.(4)

При n = 1 рівняння описує реологічну поведінку бінгамовського тіла; при n > 1 — пластичне дилатантне тіло; при n < 1 — псевдопластичне твердоподібне тіло. Твердоподібні й рідиноподібні системи відрізняються не тільки наявністю або відсутністю межі плинності, але й відмінністю в поведінці при розвитку деформацій. У структурованих рідинах (бінгамівських) із зростанням напруження зсуву спостерігається перехід до ньютонівської течії, що відповідає гранично зруйнованій структурі (рис. 2г). У твердоподібних тілах збільшення навантаження призводить до розриву суцільності тіла і його руйнування. Разом з тим є безліч систем, які мають проміжні структурно-механічні властивості.

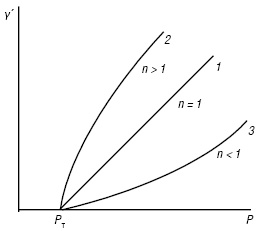
Рис. 4. Криві течії твердоподібних тіл: 1 – бінгамівське тіло; 2 – пластичне дилетантне тіло; 3 – псевдопластичне твердоподібне тіло

1.3 Трясовина - як приклад природної бінгамовської рідини

Болото - ділянка суші ( або ландшафту ), що характеризується надлишковим зволоженням , підвищеною кислотністю і низькою родючістю ґрунту , виходом на поверхню стоячих або проточних ґрунтових вод , але без постійного шару води на поверхні. Для болота характерно відкладення на поверхні ґрунту неповно розклалася органічної речовини , що перетворюється в подальшому в торф. Шар торфу в болотах не менше 30 см , якщо менше , то це заболочені землі. Болота є складовою частиною гідросфери . Перші болота на Землі утворилися на стику силуру і девону 350-400 млн років тому .

Виникненню болота сприяють 2 причини : заростання водойми або заболочування суші. Болоту характерна надмірна вологість , постійне відкладення не до кінця розкладеної органічної речовини - торфу. Здатні засмоктувати об'єкти не всі болота, а тільки ті, в яких утворилася трясовина . Трясовина болота утворюється на місці озера. Лілії і очерет на поверхні озера розростаються з часом в щільний килим на поверхні водойми. Разом з цим на дні озера розростаються водорості. У міру формування хмара водоростей та моху піднімається з дна до поверхні. Через відсутність кисню починається гниття, утворюються органічні відходи, що розходяться у воді і утворюють трясовину. Трясовина засмоктує живі об'єкти. Пояснюється це її фізичними властивостями.

Трясовина відноситься до класу бінгамовскіх рідин, фізично описаних рівнянням Бінгама - Шведова. При попаданні на поверхню об'єкта з невеликою вагою, вони поводяться як тверді тіла, тому предмет занурюватися не буде. Коли об'єкт має досить велику вагу, він тоне. Як відомо, густина болота в середньому більше, ніж у води і, до того ж, більше, ніж у людини. Так що якби тут грав роль тільки закон Архімеда, то потонути в ньому було б практично нереально. Справа вся в тому, що болото проявляє деякі ознаки, які, як відомо всім розсудливим людям, властиві рідини: воно тече, і в ньому можна потонути, а також, що важливо, властивості твердого тіла: наприклад, камені можуть лежати на його поверхні, хоча їх густина більше, ніж у болота, і, за логікою, вони повинні були б піти на дно .

Болото починає проявляти властивості рідини , коли навантаження з боку предмета перевищує деяку критичну величину. Наприклад, камінь спочатку занурюється, але, внаслідок дії сили Архімеда, його вага, скомпенсована виштовхувальною силою, не перевищує цієї самої критичної величини - занурення припиняється, виникає стан недопогруженія. Що стосується живих істот, то, коли вони ступають у болото, нога не йде до дна якраз через ефект недопогруженія. Людина, не розуміючи, що це не просто бруд, а болото, робить другий крок, злегка занурюючись обома ногами в трясовину, але не йдучи глибше. Тепер, якщо він спробує витягнути одну ногу з болота, відбудеться наступне: звичайна рідина піднімається за ногою, щоб не утворювалося порожнечі, однак болото - не є звичайною рідиною, вона зовсім не буде слідувати за ногою, під якою утворюється порожнеча, що надає додаткову силу, та повертає ногу до первісного місця занурення. Щоб подолати цю силу, доведеться робити більше навантаження на другу ногу, яка зануриться ще більше. Так будь-яка спроба витягнути вже занурену частину призведе лише до ще більшого занурення тіла.

Є 2 види занурення: недопогруженіе і перепогруженіе. Поведінка тіла, що потрапило в рідину, підпорядковується співвідношенням впливу сили тяжіння і сили Архімеда. Тіло буде занурюватися в трясовину доти, поки сила Архімеда не зрівнялась з його вагою. Якщо виштовхувальна сила менше ваги, то відбудеться недопогруженіе об'єкта, якщо більше, то - перепогруженіе. Чому перепогруженію піддаються тільки живі об'єкти? Все тому, що такі об'єкти постійно рухаються. А якщо завмерти? Чи припиниться занурення? На жаль, це лише сповільнить занурення, адже живе тіло рухається завжди, оскільки воно дихає. Неживі ж об'єкти залишаються нерухомими, тому повністю не занурюються. Перепогруженіе в трясовину і є засмоктування болота. Чому ж рух тіла прискорює занурення? Будь-який рух - це додаткова сили, що збільшує силу тиску на опору. Воно обумовлене вагою об'єкту і силою тяжіння. Різкі рухи - причина утворення під тілом областей зниженого тиску. Ці області приведуть до збільшення атмосферного тиску на живий об'єкт, що ще більше занурить його. Тому, фізичне визначення слова «засмоктування болота» виглядає так: бінгамівськая рідина ( трясовина ), намагається перевести потрапивший в неї живий об'єкт на рівень нижче нормального занурення, при якому сила Архімеда менше ваги тіла. Процес засмоктування незворотній. Потонуле тіло навіть після припинення життєдіяльності не спливе.

Відбутися таке може або в болотистій місцевості, або після сильних злив, в лісі або іншому відкритому просторі. Це може статися і після сильної посухи, коли поверхневі води випаровуються і залишаються тільки підземні, які часом ховаються під шаром мулу та їх непомітно, такі болота дуже небезпечні, тому що глибина їх може бути дуже великою і вибратися з нього практично неможливо. Імовірність бути затягнутим в болото зростає в літні та осінні періоди, взимку такого практично не відбувається, так як замерзає поверхневий шар, внаслідок чого він стає дуже міцним і піти під нього вельми проблематично. Тому саме в літній та осінній періоди потрібно бути гранично уважним і дивитися під ноги , опинившись у такій місцевості.

Правила поведінки у болоті:

Головне правило, яке потрібно знати кожному, - це не здійснювати ніяких різких рухів, опинившись у болоті. Якщо в болото засмоктує повільно, є всі шанси врятуватися.

По-перше, опинившись в болотистій місцевості, потрібно обзавестися палицею, бажано, щоб вона була широкою і міцною, то є справжній важіль. Ця палиця може виявитися вашим порятунком, тому вибирати її потрібно ретельно, а не брати перший ліпший під руку сучок.

Якщо ви потрапили в болото, зісковзнувши з купини, то вас, швидше за все, швидко засмокче, так як за інерцією ви будете продовжувати свій рух, допомагаючи тим самим трясовині, тому падати краще на живіт або спину, так вас буде засмоктувати набагато повільніше.

Якщо ви не дуже швидко рухаєтесь під воду і у вас є палиця, то її слід акуратно покласти перед собою, добре, якщо до найближчої твердині не більш півметра, тоді кінець палиці впаде на землю і вам буде легше вибратися. Але навіть якщо палиця повністю лежить в болоті, вам необхідно вчепитися в неї і постаратися перенести свій центр ваги на цю палицю, таким чином у вас вийде якась подоба містка і ви зможете вибратися на сушу або чекати допомоги, не ризикуючи остаточно піти в мул.

Якщо у вас під рукою немає абсолютно нічого такого, що могло б послужити вам важелем, постарайтеся зайняти горизонтальне положення. Робіть це якомога акуратніше, обережніше переміщаючи свій центр ваги з ніг на тулуб, якщо вам вдасться це зробити, то маса вашого тіла значно зменшиться і вас перестане затягувати в болото. У такому положенні ви можете чекати підмоги.

Але, перебуваючи в болоті, ні в якому разі не можна робити різких рухів, махати руками і намагатися смикати ногами, від цього вас ще більше засмокче безодня. Знаходяться в такому положення не можна навіть голосно кричати, закликаючи на допомогу, і тим більше розмахувати вільними кінцівками.

Якщо верх вашого тулуба ще на волі, то потрібно зняти з себе куртку або плащ і кинути його на поверхню болота, по ньому також можна вибратися, він не дасть можливості болоту засмоктати вас. Якщо в болото засмоктує дуже швидко, то допомогти може тільки стороння людина, він повинен кинути мотузку чи палицю, за якою людина, що потрапила в болото, змогла би вибратися на тверду поверхню. Іноді для того щоб витягнути одну людину з болота, потрібно не менше трьох осіб на суші, так як сила засмоктування у болота дуже велика. Слід також пам'ятати, якщо людину тягнуть з болота, то його ні в якому разі не можна відпускати, щоб зробити перепочинок, злегка відпущена людина моментально піде у трясовину, отримавши додаткову енергію з суші при відштовхуванні .

Багато тварин можуть жити та пересуватись по болоту, при цьому кінцівки у них мають більшу ніж звичайні площу. Отже для пересування болотом можна зробити плетені лижі. Відомий факт, що під час ВВВ білоруські партизани при попаданні у облогу посеред болот спаслися і перевели коней крізь болотину зробивши плетені лижі і прикріпивши їх до кінцівок коней.

ІІ.ЕКСПЕРИМЕНТАЛЬНА ЧАСТИНА

2.1 В’язкість, як основна характеристика рідин

Просте рівняння, що описує сили в'язкості, що виникають в ньютонівської рідини (які багато в чому визначають її поведінку), засноване на зсуві перебігу :

де

- Дотичне напруження, викликаного рідиною [Па]

- Динамічний коефіцієнт в'язкості - коефіцієнт пропорційності [Па с]

- Похідна швидкості в напрямку, ┴напрямку зсуву [с ^-1].

Це рівняння зазвичай використовують при течії рідини в одному напрямку, коли вектор швидкості течії можна вважати співнапрямленими(паралельним) у всіх точках розглянутого об'єму рідини.

З визначення, зокрема, випливає, що ньютонівська рідина продовжує текти, навіть якщо зовнішні сили дуже малі, аби вони не були строго нульовими. Наприклад, вода є ньютонівскою рідиною, тому що вона продовжує демонструвати властивості рідини незалежно від швидкості перемішування, на противагу неньютонівських рідин, в'язкість яких змінюється в залежності від швидкості току рідини - наприклад, перемішування може залишати "дірку" позаду (яка потроху заповнюється згодом - така поведінка спостерігається в таких речовинах, як пудинг, суспензія крохмалю в холодній воді і, в менш суворих рамках - пісок), а при зменшенні товщини шару рідини відбувається стрибок в'язкості через зміну швидкості течії рідини (це спостерігається у деяких непідтікаючих фарб, які легко наносяться, але стають дуже в'язкими на поверхні відразу після нанесення і не стікають навіть якщо поверхня вертикальна).

Для ньютонівської рідини в'язкість, за визначенням, залежить тільки від температури і тиску (а також від хімічного складу, якщо рідина не є безпримісной) і не залежить від сил, що діють на неї.

Ньютонівська рідина , в'язка рідина, що підкоряється при своїй течії закону в'язкого тертя Ньютона. Для прямолінійної ламінарного (шаруватого) течії цей закон встановлює наявність лінійної залежності (прямій пропорційності) між дотичною напругою t в плоскості зіткнення шарів рідини і похідної від швидкості перебігу u по напряму нормалі n до цієї плоскості, тобто, де h — динамічний коефіцієнт в'язкості. У загальному випадку просторової течії для Н.р. же, має місце лінійна залежність між тензорами напруги і швидкостей деформацій. Властивостями Н.р. же. володіють більшість рідин (вода, змащувальне масло і ін.) і всі гази. Перебіг Н.р. же. вивчається в гидроаеромеханике . Рідини, для яких вказані вище залежності не є лінійними, називаються неньютонівськими. До них відноситься ряд суспензій і розчинів полімерів. Такі течії вивчає реологія . Біореологія займається плинністю біологічних середовищ, а гемореологія вивчає реологію крові. Реологічні питання, пов’язані з деформацією і плинністю стоять особливо гостро, коли рідина тече по судинах дуже малих діаметрів.

Рух ньютонівської рідини (в’язкість якої постійна і не залежить від швидкості зсуву) можна описати законом Ньютона. До таких рідин відносяться легеневі гази, вода, сеча, низькомолекулярні рідини графік має вигляд прямої лінії, що проходить через початок координат.

Проте для ньютонівських рідин, в’язкість яких залежить від градієнта швидкості наприклад, при дуже малих швидкостях зсуву в’язкість крові зростає, при збільшенні ж швидкості зсуву - зменшується. Плинність починається , після перевищення деякого порогу – межа плинност. Величина характеризує пластичні властивості середовища, а нахил кривої плинності до осі - її рухливість.

Збільшення в’язкості крові при малих швидкостях зсуву спостерігається при захворюваннях і після великих травм м’язів. Коефіцієнт в’язкості крові в нормі лежить у межах (4,3-5,3)∙10^-3 Па·с, при патології він змінюється від 1,7∙10^-3 до21,9∙10^-3Па/с . У здорової людини при 37°С коефіцієнти в’язкості плазми і сироватки крові відповідно становлять η_пл=1,2∙10^-3Па/с , а η_сир= 1,1∙10^-3Па/с

У чоловіків і жінок в’язкість крові різна. У чоловіків коефіцієнт в’язкості крові у нормі становить η_кр=(4,3-5,3 ) ∙10^-3Па/с, у жінок η_кр=(3,9- 4,9 )∙10^-3Па/с.

Суттєво змінюється в’язкість крові при деяких захворюваннях. При крупозній пневмонії, бронхіальній астмі, гіпертонічній хворобі, при великих загальних інфекціях, системному атеросклерозі, перитоніті в’язкість крові підвищується і зменшується при черевному тифі, туберкульозі, анемії.

Тому вимірювання в’язкості речовин має важливе значення не тільки у техніці, харчовій промисловості та у медицині для діагностики захворювань.

2.2 Способи вимірювання в’язкості

Прилади для вимірювання в'язкості називаються вискозиметрами. У віскозиметра використовуються два різних принципи:

-за швидкістю витікання рідини з малого отвору або з капіляра;

-за швидкістю падіння кульки в в'язкої рідини.

Перший принцип заснований на формулі Пуазейля, що дає залежність між обсягом рідини, яка витікає з трубки радіусом R і довжиною I:

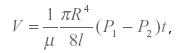(1)

де P 1 і P 2 - тиск на торцях трубки; R - радіус трубки; I - довжина; t - час витікання.

Другий принцип вимірювання в'язкості заснований на вимірюванні швидкості падіння кулі у в'язкому середовищі (формула Стокса):

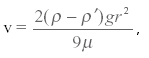
(2)

де v-швидкість падіння кулі в рідині; ρ - щільність матеріалу кулі; ρ '- щільність рідини; r - радіус кулі.

Одним з широко використовуваних приладів для вимірювання в'язкості є віскозиметр Енглера, в якому вимірюється час витікання 200 р. рідини в порівнянні з часом витікання 200 г води через той же отвір. В'язкість вимірюють у градусах Енглера, що відповідає відношенню часу витікання рідини до часу витікання води при тих же умовах. Співвідношення між пуаз і градусами Енглера дається формулою:

(3)

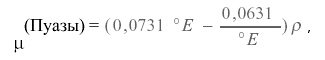
де р - щільність рідини в г/см ³.

В'язкість, позначена у формулі (3) і визначена через силу опору руху називається ще динамічною в'язкістю. Існує поняття кінематичної в'язкості - це в'язкість, віднесена до густини, тобто:

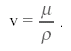
(4)

Вимірюється кінематична в'язкість в одиницях тобто м² /с в системі СІ. Та ж одиниця в СГС-системі називається Стокс, т. е.

(5)

Існує ще поняття ударної в'язкості, яка визначається, як робота для зламу твердого тіла, віднесена до одиниці поперечного перерізу зламу.

(6)

Величина обернена в'язкості називається плинністю:

(7)

Іноді в техніці користуються поняттям питомої в'язкості, тобто відношенням в'язкості рідини до в'язкості води:

(8)

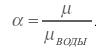
Вязкість рідин при 25 ° C

Рідина:	В'язкість [Па·с]	В'язкість [мПа·с]
ацетон	3.06·10⁻⁴	0,306
бензол	6.04·10⁻⁴	0,604
кров (при 37 °C)	(3–4)·10⁻³	(3–4)
касторове масло	0.985	985
кукурудзяний сироп	1.3806	1380,6
етиловий спирт	1.074·10⁻³	1.074
етиленгліколь	1.61·10⁻²	16,1
гліцерин (при 20 °C)	1.49	1490
мазут	2.022	2022
ртуть	1.526·10⁻³	1,526
метиловий спирт	5.44·10⁻⁴	0,544
моторна олива SAE 10 (при 20 °C)	0.065	65
моторна олива SAE 40 (при 20 °C)	0.319	319
Нітробензол	1.863-10^∙10⁻³	1,945
оливкова олія	0,08 1	81
сірчана кислота	2.42·10⁻²	24.2
вода	8.94·10⁻⁴	0,894

В'язкість залежить від тиску, температури, а також іноді від градієнта зсуву (неньютонівські середовища; їхня в'язкість охоплює і так звану структурну в'язкість). Рідини, в'язкість яких не залежить від градієнту зсуву, називають ідеально в’язкими (ньютонівськими). В'язкість рідин у загальному випадку з зменшується.

2.3 Вимірювання динамічної та кінематичної в’язкості

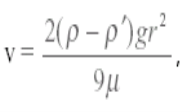Скористаємось другим принципом вимірювання в'язкості заснованим на вимірюванні швидкості падіння кулі у в'язкому середовищі (формула Стокса):

v-швидкість падіння кулі в рідині;

ρ - густина матеріалу кулі;

ρ '- густина рідини;

r - радіус кулі.

1. Обчислимо швидкість падіння кульки у рідині за формулой:

, S- висота стовпа рідини,

t- час падіння кульки в рідині.

2. Динамічну в’язкість визначимо використовуючи формулу Стокса:

v-швидкість падіння кулі в рідині;

ρ - густина матеріалу кулі;

ρ '- густина рідини;

r - радіус кулі.

3. Кінематичну в’язкість визначимо за відношенням динамічної в’язкості до густини рідини:

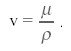
4. Обчислимо плинність рідин за формулою:

5. Іноді в техніці користуються поняттям питомої в'язкості, тобто відношенням в'язкості рідини до в'язкості води:

Обчислення густини кульки та рідин показано в Таблиці 1.

Таблиця 1

Рідина	Маса порожньої склянки(кг)	Маса склянки з рідиною(кг)	Маса рідини Тіла(кг)	Об’єм рідини М³	Густина рідини кг/м³
кулька	─	─	2,5∙10^-3	0,27∙10^-6	9,3∙10³
вода	─	─	─	─	1∙10³
Моторна олива	49,55∙10^-3	67,32∙10^-3	17,8∙10^-3	20∙10^-6	0,89∙10³
Згущене молоко(1)	49,55∙10^-3	76,84∙10^-3	27,3∙10^-3	20∙10^-6	1,37∙10³
Згущене молоко(2)	49,55∙10^-3	73,12∙10^-3	23,6∙10^-3	20∙10^-6	1,18∙10³
Розчин крохмалу	49,55∙10^-3	85∙10^-3	35,45∙10^-3	30∙10^-6	1,18∙10³
Олейна	49,55∙10^-3	64,57∙10^-3	15∙10^-3	20∙10^-6	0,75∙10³

Виконаємо розрахунок швидкості кульки при падінні в рідинах, дані подано у Таблиці 2:

Таблиця 2

рідина	Висота стовпа рідини, м	Час падіння,с	Швидкість падіння кульки. м/с
вода	28,3∙10^-2	0,01	28,3
Моторна олива	19∙10^-2	0,2	0,92
Згущене молоко 1	14,5∙10^-2	41,1	0.0035
Згущене молоко 2	14,5∙10^-2	38,4	0,0038
Розчин крохмалу	14,5∙10^-2	8,4	0,017
Олейна	19∙10^-2	0,06	3,67

Обчислення в’язкості подано у Таблиці 3

Таблиця3

рідина	Динамічна в’язкість ,μ	Кінематична в’язкість,ν	Плинність,φ	Питома в’язкість ,α
вода	0.01	0.01∙10^-3	100	12
Моторна олива	0,318	0,36∙10^-3	3,14	355,7
Згущене молоко	7,9	0,57	0.12	9.4∙10⁴
Згущене молоко	5,7	0,48	0,18	6,8∙10⁴
Розчин крохмалу	16	0,014	0.063	1,9∙10⁴
Олейна	0,081	0,12	12,3	96.6

Висновки

Фізичні властивості речовин ґрунтується на їх деформаційній поведінці та текучості. Ці властивості мають велике значення, як для оцінювання якості речовин, так і для визначення здатності речовин до переробки. Для характеристики різних речовин використовують фундаментальні та складні властивості. Фундаментальні властивості: пружність, пластичність, в’язкість . Складні властивості- це сукупність фундаментальних властивостей.

Ньютонівські рідини- це рідини яким властива тільки в’язкість, тому вони називаються «в’язкими рідинами.» Бінгамівські рідини мають властивість в’язкості та пластичності. Дослідження текучості Бінгамівських рідин дає можливість розв’язати ряд прикладних задач:

стискання рідини між двома паралельними пластинами;
текучість середовища з мякої ємкості при стисканні її між паралельними та не паралельними пластинами ;
виштовхування рідини з каналів різних форм.

За результатами дослідження поведінки бінгамівських рідин виявили як запобігти явищу перепогруження у рідину.

При опрацюванні теоретичного матеріалу визначили, що в’язкість рідин також визначається для проведення діагностики захворювань у медицині. Як відомо кров, плазма і сироватка крові є прикладом бінгамівських рідин, а показник в’язкості крові у здорової та хворої людини мають різні значення. Збільшення в’язкості крові при малих швидкостях зсуву спостерігається при захворюваннях і після великих травм м’язів.Отже з метою діагностики різних видів захворювань проводять аналіз в’язкості плазми і сироватки крові.

Отже вимірювання в’язкості речовин має важливе значення не тільки у техніці, харчовій промисловості, але й у медицині.

Тверде тіло Рідина

Тв. Тіло деформоване в’язка ідеальна

Евклідове тв. тіло рідина рідина Паскаля

Ідеально- неідеально неньютонівська класична

пружне Гукове пружне тіло рідина ньютонівська

тіло рідина

Список використаної літератури

1. Гноевой А.В., Климов Д.М., Чесноков В.М. Исследование тече-

течений вязкопластичных сред в каналах и полостях с изменяемыми

268 Список литературы

формами их стенок (элементы теории и техническое приложе-

приложение).—М.: Полиграф сервис, 1995.— 128 с.

2. Гноевой А.В., Климов Д.М., Чесноков В.М. К теории течений

бингамовских сред. — М., 1998. — 68 с. (препр. / ИПМ РАН;

№626).

3. Гноевой А.В., Климов Д.М., Чесноков В.М. Об одном методе

исследования пространственных течений вязкопластичных сред //

МТТ.-1993.-№5.-С. 150-158.

4. Р. Фейнман, Р. Лейтон, М. Сендс «Фейнмановские ЛЕКЦІЇ З

ФІЗИКИ» 1976р.

5. «Елементарний підручник фізики» під ред. Академіка Г.С.

Ландсберг 1971р.

6. Перельман Я.І. «Цікава фізика» 1999р.

7. http://i-fakt.ru/pochemu-boloto-zasasyvaet/

doc

Завантажити

Зберегти на потім

Додав(-ла)

Коновалова Світлана Євгеніївна

Пов’язані теми

Фізика, Інші матеріали

Додано

29 січня 2023

Переглядів

3340

Оцінка розробки

Відгуки відсутні