Об’єм піраміди та конуса. Розв’язування задач

Тема заняття: Об’єм піраміди та конуса. Розв’язування задач.

Мета заняття:     

Навчальна: домогтися засвоєння формули для  обчислення об’єму піраміди та конуса; сформувати вміння розв’язувати задачі, що передбачають застосування формули для обчислення «Об’єм піраміди та конуса».

             розвиваюча: формувати вміння аналізу­вати відповіді однокурсників, до­водити власну точку зору; розви­вати логічне мислення, культуру математичного мовлення, спосте­режливість, уважність, терпіння, уміння зосереджувати увагу.

              виховна: виховувати увагу, спостережливість, наполегливість у навчанні, культуру математичного запису та акуратність рисунків, виховувати інтерес до математики.                                      

Тип заняття: засвоєння нових знань і вмінь.

                   Хід заняття

І. Організаційний етап.

ІІ. Перевірка домашнього завдання.

1. Перевірити наявність виконаного домашнього завдання та відповіс­ти на запитання, які виникли у студентів при розв'язуванні задач.

2. Математичний диктант.

 Бічне ребро прямої призми дорівнює 8 см, а в основі лежить прямокутний трикутник з гіпотенузою 10 см і катетом 8 см.             

Знайдіть:

1) довжину третього ребра основи;

2) площу основи;

3) радіус кола, описаного навколо основи призми;

4) площу бічної поверхні призми;

5) площу повної поверхні призми;

6) обʼєм призми.

ІІІ. Актуалізація опорних знань.

1.Повторення теоретичного матеріалу. 

Дати відповіді на запитання :                                             

1. Що таке піраміда?

2.Яку піраміду називають правильною?

3. Куди проектується вершина піраміди, якщо всі бічні ребра нахилені під одним кутом до площини основи?

4. Куди проектується вершина піраміди, якщо всі бічні грані нахилені під одним кутом до площини основи?

5.Як визначити кут між бічною гранню піраміди та площиною основи?

6. Що таке конус ?

7. Що називається твірною конуса?

8. Як нахилені твірні конуса до площини основи?

9.Яку геометричну фігуру утворює переріз конуса площиною, яка проходить через його вершину?

10.Як визначити кут між твірною та площиною основи конуса?

Завдання

Записати формули, за якими обчислюється :

1.Площа квадрата, у якого відома сторона.

2. Площа трикутника, у якого відомо сторона  та проведена до неї висота.

3. Площа трикутника,у якого відомо дві сторони і кут між ними.

4. Площа круга.

5.Площа квадрата, у якого відома діагональ.

6. Площа трикутника, у якого відомо три сторони .

7. Площа прямокутного трикутника.

8. Площа рівностороннього трикутника.

IV. Формування нових знань і вмінь.

План

1. Об’єм піраміди
2. Об’єм конуса
3. Розв’язування задач

Теорема

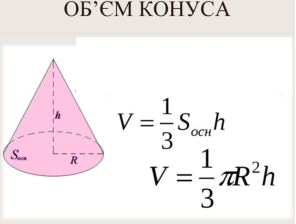
Об'єм будь-якої піраміди дорівнює третині добутку площі її основи на ви­соту, тобто V = SH , де S — площа основи піраміди, Н — її висота.

Розв'язування задач (усно)

2. Сторона основи правильної трикутної піраміди дорівнює 4 см, висота піраміди дорівнює 6 см. Знайдіть об'єм піраміди.

3. Обчислити об’єм піраміди з площею основи 5 с і висотою 18 см.

4. Обчислити об’єм конуса  з радіусом 3см і висотою 2см.

6. Осьовим перерізом конуса є рівносторонній трикут­ник зі стороною

4 см. Обчисліть об’єм конуса.

Застосування знань і вмінь

1.      Розв'язування задач (письмово)

1. У правильній чотирикутній піраміді висота дорівнює 3 см, бічне ребро — 5 см. Знайдіть об'єм піраміди.

 2. Сторона основи правильної трикутної піраміди дорівнює а, а бічне ребро утворює з площиною основи кут α. Знайдіть об'єм піраміди.

Розв'язання

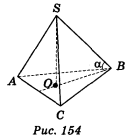Нехай SABC — правильна піраміда (рис. 154), в якій АВ = ВС = АС = а;  SO (АВС); <SBO = а. Площа основи S₁ = = , OB — радіус кола, описаного навколо трикутника АВС, тому 0В ==. Далі із ΔSOB SO = OB tg<SBO=tgα . Отже, шуканий об'єм V дорівнює:     V = S₁ · SO = · · tg α = .

Відповідь. .

3. Висота правильної чотирикутної піраміди дорівнює Н, а бічна грань утворює з основою кут α. Знайдіть об'єм піраміди.

Розв'язання

Нехай SABCD — правильна чотирикутна піраміда (рис. 155), в якій SO(АВС), SO = Н. Проведемо OKDC, за теоремою протри перпен­дикуляри маємо: SK CD; отже, <SKO = α.

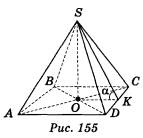Із ΔSKO OK = OS ctg <SKO = H ctg α.

Оскільки AD = 2·OK , то одержуємо: AD = 2Hctgα. Тоді площа ос­нови      S₁ = AD² = 4H² ctg²α. Отже, шуканий об'єм

V = S₁·OS = H² ctg^гα · H = Н³ ctg² α.

Відповідь. Н³ ctg² α.

Задачі на об’єм конуса

1. Осьовий переріз конуса — прямокутний трикутник із гіпотенузою 12 см. Знайдіть об'єм конуса. (Відповідь. 72π см³.)

2. Із центра основи конуса проведено перпендикуляр до твірної, який утворює з висотою кут р. Знайдіть об'єм конуса, якщо його твірна дорівнює l.

(Відповідь. cos² β sin β .)

Підведення підсумку заняття

Запитання до групи

1) Чому дорівнює об'єм будь-якої піраміди?

2) Запишіть формулу для обчислення об'єму піраміди.

3) Чому дорівнює об'єм конуса?

4) Запишіть формулу для знаходження об'єму конуса.

5) Дано конус, у якого радіус основи ОА = 8 см і висота SO = 15 cm. Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) катети прямокутного трикутника SOA дорівнюють 17 см і 8 см;

б) осьовим перерізом конуса є прямокутний трикутник із гіпотену­зою

SA = 17 см;

в) твірна конуса дорівнює 15 см;

г) об'єм конуса дорівнює π · 8² · 15 см³.

V. Домашнє завдання