Округлення десяткових дробів.

Тема. Округлення десяткових дробів.

Мета: ознайомити учнів з поняттям округлення чисел до певного роз­ряду; формувати вміння використовувати правило округлення чисел для розв'язання вправ.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця округлення десяткових дробів.

Хід уроку

І. Актуалізація опорних знань

Запитання до класу

1. Назвіть розряди числа 53,6171.
2. Знайдіть координати точок, зображених на рис. 129.

Між якими сусідніми натуральними числами лежать координати то­чок А, В, С? До якого з натуральних чисел ближче кожне з цих чисел? Які числа знаходяться на однаковій відстані?

3. Знайдіть площу прямокутника зі сторонами:
   1) 17 м і 36 м; 2) 29 м і 24 м.

Виразіть цю площу в сотках. Між якими сусідніми натуральними чис­лами знаходяться отримані числа? До якого з них ближче кожне з отрима­них чисел?

4. Хлібина коштує 1 грн. 50 к. Скільки коштує 1) півхлібини; 2) чверть хлібини?

II. Мотивація навчальної діяльності

Запитання до класу

1. Чи знаєте ви:

1) Скільки людей живе в Україні?

2) Скільки кубічних метрів містить Чорне море?

3) Скільки волосинок росте на голові людини?

4) Скільки тонн снігу випало торішньої зими?

(Зрозуміло, що більшість учнів не зможе точно відповісти на запитання.)

2. Чи можна знайти точні числа, що є відповідями на попередні запитання?

(Вчитель наголошує, що за певних причин точних відповідей знайти неможливо, тому замість них беруть інші значення, близькі до шуканих, які є круглими і на прикладі досить часто ми маємо справу саме з набли­женими значеннями величин.)

Наша мета — встановити правило округлення.

ІІІ. Формування знань учнів про десяткові дроби

Розглянемо числа: 1,2; 1,5; 1,9 — вони мають цілу частину — 1, отже, лежать між сусідніми натуральними числами 1 і 2. Але 1,2 ближче до 1, а 1,9 — до 2. Тому можна сказати, що 1,2 = 1 (приблизно дорівнює 1), а 1,9 = 2. Серед інших десяткових дробів з однією цифрою після коми і цілою частиною 1 є ще кілька чисел, що лежать ближче до 1 (це 1,1; 1,3; 1,4), і кілька чисел, що лежать ближче до 2 (до 1,6; 1,7; 1,8), тому 1,1 = 1; 1,3 = 1; 1,4 = 1, але 1,6 = 2; 1,7 = 2; 1,8 = 2 при цьому можна помітити, що в отриманих числах цифри, що йшли після коми, відсутні, а остання циф­ра, що залишилась, є цифрою розряду одиниць, і вона співпадає з циф­рою розряду одиниць, що були в даному числі, якщо за нею йшли цифри 1; 2; 2; 4, і ця остання цифра збільшилась на 1 у випадку, коли за нею йшли цифри 6, 7, 8, 9.

Цю операцію називають округленням десяткових дробів до < розряду > одиниць і правило, що описує розв'язування подібних задач, можна сформулювати так:

1. Під час округлення десяткового дробу до одиниць (десятих, сотих і т. д.), усі наступні за цим розрядом цифри відкидають.
2. Якщо при цьому перша з цифр, які відкидають, 0,1,2,3,4, то остання з цифр, яку залишають, не змінюється.
3. Якщо ж перша з цифр, які відкидають, дорівнює 5,6,7, 8 або 9, то ос­танню з цифр, яку залишають, збільшують на 1.

(Якщо в учнів виникли запитання про цифру 5, яка не розглядалась у прикладах, варто пам'ятати, що існує домовленість щодо цієї цифри, яка й покладена в правило.)

Після цього варто розглянути, прокоментувати і записати декілька прикладів на округлення. Записи можна робити так:

Приклад 1. Округлити: 1) до одиниць; 2) до сотих; 3) до тисячних число 53,6171.

1) 53,6171 54; 2) 53,6171 53,62; 3) 53,6171 53,617.

Зауважимо, що під час округлення натуральних чисел (див. запитан­ня, п.II) правило дещо зміниться, а саме: замість цифр, що стоять у нату­ральному числі після даного розряду, до якого округляють, пишуть нулі.

Приклад 2. Округлити число 9762:

1) до десятків; 2) до сотень; 3) до тисяч.

1) 9762 9760; 2) 9762 9800; 3) 9762 10000.

IV. Закріплення знань. Формування вмінь

Усні вправи

1. Прочитайте і скажіть, до якого розряду округлили число:

1) 3,543 3,5; 2) 7,318 7; 3) 14,5 10; 4) 0,6173 0,617.

2. Робота з таблицею «Округлення десяткових дробів»

Округліть дроби:

Письмово за підручником учні виконують вправи №№ 816, 818, 820 (а), 812 (1; 2).

 Зауважимо, що не треба вимагати від учнів завчання тексту, виділено­го у п. 29 жирним курсивом. Доцільно тільки вимагати засвоєння алго­ритму, який можна записати і використовувати у вигляді схеми:

1. Знайди цифру того розряду, до якого округлили десятковий дріб (на­туральне число).
2. Подивись на наступну (читаючи зліва направо) цифру; якщо вона 0, або 1, або 2, або 3, або 4 — цифру в п. 1 не змінюй, в інших випадках — збільш її на 1 (+ 1).
3. Усі цифри, що передують знайденій у п. 1, — перепиши, ті, що йдуть за нею, — відкинь (запиши нулями).

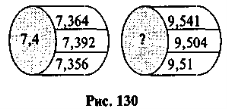V. Підсумок уроку
Запитання до класу

Знайдіть пропущене число (рис. 130)

(Пояснюючи, як знайдено правиль­ну відповідь — 9,5, учні повторюють ал­горитм округлення чисел.)

VI. Домашнє завдання

п. 29, №№817 (перші з чисел в кожному з розділів), №819, 821 (3; 4).