Оптимізація та активізація навчального процесу за допомогою дидактичних ігор

           Оптимізація та активізація навчального процесу за допомогою дидактичних ігор

         Сучасним методом навчання та виховання, яке сприяє оптимізації та активізації навчального процесу та дозволяє показати цікаві та захоплюючі грані математики, є дидактична гра.   Поєднання навчальної спрямованості та ігрової форми дозволяє стимулювати невимушене оволодіння конкретним навчальним матеріалом. Дидактична гра має чітку структуру, яка вирізняє її серед іншої діяльності. Основні структурні компоненти дидактичної гри: ігровий задум, правила, ігрові дії, пізнавальний зміст чи дидактичне завдання, обладнання, результат гри. На відміну від ігор взагалі дидактична гра має суттєву ознаку - наявність чітко визначеної мети навчання та відповідного їй педагогічного результату, які можуть бути обґрунтовані, подані наочно та характеризуються пізнавальною спрямованістю.

         Ігровий задум – перший структурний компонент гри, закладений у дидактичне завдання, що необхідно виконати під час навчання. Ігровий задум найчастіше виступає у вигляді питання чи загадки, яка ніби проектує перебіг гри. Це надає грі пізнавального характеру, висуває до її учасників певні вимоги щодо знань.

Кожна дидактична гра має правила, які визначають порядок дій і поведінка учнів у процесі гри, сприяє створенню під час уроку робочої атмосфери. Тому правила дидактичних ігор необхідно розробляти з урахуванням мети уроку та індивідуальних можливостей учнів. Це створює умови проявів самостійності, наполегливості, розумової активності.

Крім того, правила гри виховують уміння керувати своєю поведінкою, узгоджувати та підпорядковувати її до вимог колективу.
Істотними у дидактичній грі є дії, що регламентуються правилами гри, сприяють пізнавальній активності учнів, надають їм можливість виявити свої здібності, застосувати наявні знання, вміння та навички для досягнення цілей гри. Дуже часто ігровим діям передує розв'язання задачі.

Вчитель, керуючи грою, спрямовує її у належне дидактичне русло, при необхідності активізує її перебіг різноманітними прийомами, підтримує інтерес до гри, підбадьорює відстаючих.
Основою дидактичної гри є пізнавальний зміст, який полягає у засвоєнні тих знань та умінь, які застосовуються під час розв'язання навчальної проблеми, поставленої грою.

Під час організації дидактичних ігор на уроках необхідно дотримуватись таких положень:

 1) правила гри повинні бути простими, чітко сформульованими, а математичний зміст матеріалу – доступно розумінню учнів;

 2) завдання гри повинні містити достатню кількість інформації для активної мисленнєвої діяльності учнів на уроці, який забезпечуватиме досягнення розвиваючої та навчальної цілей уроку;
3) дидактичний матеріал, який використовується в процесі гри, має бути цікавим, педагогічно доцільним та зручним у користуванні; 4) якщо дидактична гра має характер змагання, слід забезпечити справедливий і об'єктивний контроль її результатів;

5) кожен учень має бути активним учасником дидактичної гри;
6) якщо на уроці створюється кілька ігрових ситуацій, їх варто розподілити за складністю математичного матеріалу, що до них входить, або характером розумових дій, які необхідні для їх виконання; якщо на кількох уроках поспіль проводяться дидактичні ігри, які вимагають аналогічних розумових дій від учнів, то за змістом математичного матеріалу вони повинні відповідати принципу: від простого до складного, від конкретного до абстрактного;
7) необхідно дотримуватись заходів використання дидактичних ігор у навчанні, щоб учні не звикли в усьому бачити лише гру;

8) під час дидактичної гри від учнів слід вимагати чіткого та грамотного вираження своїх думок, проведення послідовних логічних міркувань, обґрунтування висновків;
9) дидактична гра буде результативнішою, якщо вона закінчиться на тому ж уроці, на якому і почалася.
  Урок – екскурсія, урок-подорож, урок-експедиція чи заочна подорож

План проведення.
1. Повідомлення теми.
2. Вступне слово ведучого.
3. Пояснення нового матеріалу шляхом екскурсії, що імітується, - проводить екскурсовод-вчитель.
4. Відповіді на запитання, що виникли під час екскурсії.
5. Подарунки та сувеніри на згадку (готувати заздалегідь).

Урок – аукціон.
На початок "аукціону" експертами визначається "продажна вартість" ідей. Потім ідеї "продаються", автор ідеї, який одержав велику ціну, визнається переможцем. Ідея переходить до розробників, що доводять свої варіанти. Аукціон може бути проведено у два тури. Ідеї, які пройшли у другий тур, можуть бути випробувані у практичних завданнях.

 

 

 

 

УРОК-АУКЦІОН У 7 КЛАСІ

Тема: Трикутники.

Мета уроку: систематизація та узагальнення знань; збудження інтересу до предмета; розвиток уваги і спостережливості.

Обладнання уроку: рисунки із зображенням трикутників; різнокольорові, вирізані з цупкого паперу трикутники; гонг, молоток.

Форма проведення уроку: гра „Аукціон”.

ХІД УРОКУ

І. Вступне слово вчителя

Увага! Увага! Сьогодні замість уроку геометрії у нас відбудеться аукціон-розпродаж геометричних фігур.

Що таке аукціон?

Аукціон – це публічний продаж майна, під час якого покупцем стає той, хто запропонує більш високу ціну. Учасники аукціону називаються аукціонерами, людина, яка проводить аукціон, – аукціоністом, а товар – лотом.

На наш аукціон надіслано кілька фігур.

Умова: хто одразу дає точне означення фігури, той її і купує. Якщо в когось будуть уточнення і доповнення, фігуру буде продано тому, хто закінчить повну відповідь. Отже, намагайтеся одразу дати повну відповідь. Бажаючі відповісти (тобто купити фігуру), піднімають руку. Хто перший підніме – той і починає.

Аукціоніст після кожної неповної відповіді буде вдаряти в гонг до трьох разів, доки не з'явиться учень (аукціонер), який виявить бажання доповнити відповідь.

Зауваження. У випадку, якщо не знайдеться учня, який захоче доповнити, тобто завдання виявиться занадто складним, фігуру доведеться продати попередньому покупцеві. Однак у цьому випадку вчителю доведеться самому доповнити відповідь, щоб не лишати прогалин у знаннях учнів.

У ході продажу фігур (лотів) № 10, 11, 12, 13, 14 доведення рівності трикутників доцільно записувати на дошці, щоб учні ще раз могли простежити відповідність рівних кутів та рівних сторін і пригадати ознаки рівності трикутників. Для цього вчитель може скористатися допомогою помічника – одного з учнів класу. Той самий помічник може допомагати вчителю (аукціоністу) під час проведення аукціону – відзначати, хто перший підвів руку для відповіді. Помічником може бути учень з найнижчим рівнем навчальних досягнень з геометрії, аби, по-перше, залучити і його до процесу, по-друге, надати йому значущості в очах товаришів.

Якщо для відповіді кілька учнів піднімають руку одночасно, треба урізноманітнювати їх виклик, щоб залучити до участі в аукціоні якомога більше школярів.

Усі фігури, що виставляють на продаж, слід зобразити заздалегідь на окремих альбомних аркушах, вирізати з цупкого паперу і розфарбувати.

Аукціон можна розпочинати.

II. Розпродаж геометричних фігур і задач

1.                 На продаж виставляється довільний трикутник. Дати означення трикутника.
2.                 Продається гострокутний трикутник. Дати його означення.
3.                 Продається тупокутний трикутник. Дати його означення.
4.                 Продається прямокутний трикутник. Дати його означення.
5.                 Продається рівносторонній трикутник. Дати його означення.

1.                 Продається рівнобедрений трикутник. Дати його означення і назвати властивості.

6.                 Продається трикутник зі своєю медіаною. (На моделі довільного трикутника виділити медіану.)

Дати означення медіани трикутника.

8)Продається трикутник з бісектрисою.

(На моделі довільного трикутника виділити будь-яку його бісектрису.) Дати означення бісектриси трикутника.

9)Продається трикутник з висотою.

(На моделі довільного трикутника виділити його висоту.) Дати означення висоти трикутника.

10)Продається пара рівних трикутників.

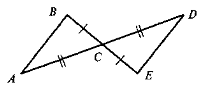(На альбомному аркуші зображені два трикутники, що мають дві пари рівних сторін і кути між ними — вертикальні.)

 

Цей лот може придбати той, хто скаже, за якою ознакою трикутники рівні, і, називаючи рівні трикутники, правильно вкаже відповідні вершини (тобто вимовить: трикутник... дорівнює трикутнику... за двома сторонами і кутом між ними).

11) Продається пара рівних трикутників.

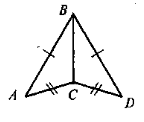(На альбомному аркуші зображені два трикутники, що мають дві пари рівних сторін і одну спільну сторону.)

Назвати рівні трикутники і вказати відповідну ознаку (відповідаючий має сказати: трикутник... дорівнює трикутнику... за трьома сторонами).

12) Продається пара рівних трикутників.

(На альбомному аркуші зображені два трикутники, що мають пару рівних сторін, спільну сторону і прилеглі до неї рівні внутрішні різносторонні кути.)

Назвати рівні трикутники і довести їх рівність.

(Відповідь. Трикутник... дорівнює трикутнику... за двома сторонами і кутом між ними.)

13) Продається пара рівних трикутників.

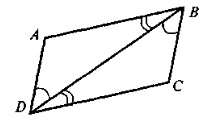(На альбомному аркуші зображені два трикутники, що мають спільну сторону і прилеглі до неї дві пари рівних внутрішніх різносторонніх кутів.)

Назвати рівні трикутники і довести їх рівність.

(Відповідь. Трикутник... дорівнює трикутнику... за стороною і прилеглими кутами.)

14) Продається пара рівних трикутників.

(На альбомному аркуші зображені два трикутники, що мають пару вертикальних кутів, пару рівних внутрішніх різносторонніх кутів і пару рівних сторін.)

Назвати рівні трикутники і довести їх рівність.

(Очікувана відповідь. Трикутник... дорівнює трикутнику... за стороною і прилеглими кутами.)

Урізноманітнити завдання, повторити геометричні відомості, здобуті в 6 класі, та надихнути учнів на вивчення наступної теми „Коло і круг” допоможуть завдання 15–16.

15)Продається коло.

(Демонструється модель кола, на якій яскравими кольорами зображені центр, діаметр, хорда.)

Дати означення кола, назвати його центр, радіус, діаметр, хорду.

16)Продається ще одне коло.

(На моделі кола яскраво зображені центр, радіус, діаметр, що не містить цього радіуса, хорда.)

Дати означення радіуса, діаметра, хорди.

III. Підсумки уроку

Аукціон завершено. У ході аукціону ми узагальнили відомості про трикутник та його елементи, види трикутників, ознаки рівності трикутників, пригадали означення кола та його елементів.

IV. Домашнє завдання

Доберіть або самі складіть задачі для продажу на аукціоні

 

 

УРОК-ПОДОРОЖ У 9 КЛАСІ

Тема. Площі многокутників.

Мета: систематизувати знання, вміння та навички учнів розв'язувати задачі на знаходження площ многокутників; розвивати пам'ять, логічне мислення, мову учнів; виховувати інтерес до математики, увагу, наполегливість, самостійність, охайність.

Запам'ятай, що Гаусс всім сказав:

Є математика царицею наук.

І недарма він всім заповідав

Творити в вогнищі робіт і мук.

Безмежна роль її у відкритті законів,

У створенні машин — повітряних, земних.

І було б важко нині без Ньютонів,

Без звершень, відкриттів нових.

 Нехай не станеш Піфагором ти,

Яким у мріях вирости бажаєш,

Та будеш ти людиною завжди

І Україну вславиш добрими ділами.

ХІД УРОКУ

Учитель. Математика цікава тоді, коли дає поживу нашій винахідливості, уяві, здатності до міркувань.

Уявіть себе не учнями 9-го класу, а пасажирами математичного поїзда, що вирушає в подорож по країні Геометрія до міста Площеград. Для того щоб потрапити в математичний поїзд, вам потрібно придбати квитки. Але не за гривні. Квитки отримаєте, якщо проявите розум, кмітливість та розв'яжете задачі.

Станція „Стартова”

Квиток 1

1.               Знайти площу трапеції, якщо її основи дорівнюють 7,5 см і 10,5 см, а висота – 11 см.
2.               Знайти площу квадрата, якщо його периметр дорівнює 20 см.

Квиток 2

1. Знайти площу ромба, сторона якого дорівнює 21 см, а висота – 10,5 см.

2. Знайти площу правильного трикутника; сторона якого дорівнює 5 см.

Квиток 3

1.                                                                                                          Знайти площу квадрата, сторона якого дорівнює 4 см.
2.               Знайти площу прямокутника, довжина якого дорівнює 11 см, а ширина – 10 см.

Квиток 4

1.                                                                                                       Знайти площу ромба, діагоналі якого дорівнюють 15 см і 20 см.
2.               Знайти площу паралелограма, основа якого дорівнює 25 см, а висота – 10 см.

Квиток 5

1. Знайти площу прямокутника, довжина якого дорівнює 9 см, а ширина – 10 см.

2. Знайти площу квадрата, сторона якого дорівнює 7 см.

Квиток 6

1. Знайти площу прямокутного трикутника, катети якого дорівнюють 11 см і 20 см.

2. Знайти площу прямокутника сторона якого дорівнює 15 см, а ширина - 10 см.

Квиток 7

1. Знайти площу паралелограма, сторони якого дорівнюють 10 см і 15 см, а кут між ними 30°.

2. Знайти площу правильного трикутника, сторона якого дорівнює 8 см.

Квиток 8

1. Знайти площу ромба, діагоналі якого дорівнюють 25 см і 12 см.

2. Знайти площу трикутника, основа якого дорівнює 10 см, а висота – 7 см.

Квиток 9

1. Сторона правильного трикутника дорівнює см. Знайти його площу.

2. Сторона квадрата дорівнює 11 см. Знайти його площу.

 

Квиток 10

1. Знайти площу правильного трикутника, сторона якого дорівнює см.

2. Знайти площу ромба, діагоналі якого дорівнюють 25 см і 16 см.

Квиток 11

1.               Знайти площу трикутника, якщо основа його дорівнює 11 см, а висота – 10 см.
2.               Знайти площу прямокутника, довжина якого дорівнює 19 см, а ширина – 14 см.

Квиток 12

1.               Знайти площу квадрата, якщо його периметр дорівнює 24 см.
2.               Знайти площу прямокутного трикутника, катети якого дорівнюють 35 см і 20 см.

Квиток 13

1. Знайти площу трикутника, дві сторони якого дорівнюють 11 см і 10 см, а кут між ними – 30°.

2. Знайти площу ромба, діагоналі якого дорівнюють 15 см і 20 см.

Квиток 14

1.               Площа паралелограма дорівнює 250 см², основа – 25 см. Знайти висоту.

1.               Знайти площу рівностороннього трикутника, сторона якого дорівнює м.

Квиток 15

1.               Знайти площу прямокутного трикутника, катети якого дорівнюють 21 см і 12 см.
2.               Знайти площу ромба, діагоналі якого дорівнюють 21 см і 12 см.

Квиток 16

1.               Знайти площу прямокутника, довжина якого дорівнює 16 см, а ширина – 9 см.
2.               Знайти площу трикутника, основа якого дорівнює 16 см, а висота – 11 см.

Квиток 17

1. Знайти площу паралелограма, сторони якого дорівнюють 11 см і 16 см, а кут між ними 45°.

2. Знайти площу рівностороннього трикутника, сторона якого дорівнює см.

Учитель. Посадка закінчується. Провідник перевірить, чи білети справжні. (А він знає свою справу!) Поїзд відбуває до наступної станції.

Станція „Детективна”

Учитель. Знайдено аркуші паперу з розмитими цифрами, знаками, буквами (їх позначено зірочками *). Необхідно їх відновити, інакше поїзд далі не рушить.

ТРИКУТНИКИ

1.           
2.           

 

3.           
4.           

 

ЧОТИРИКУТНИКИ

1.           
2.           
3.           

4.           
5.           
6.           

Учитель. Формули ви знаєте, нам дозволено рухатися далі.

Станція „Історична”

Учитель. Сподіваюся, вивчати формул и в XXI ст. декого стимулюватиме той факт, що 4–5 тисяч років тому вавілоняни вміли знаходити площі прямокутника, трапеції, трикутника. Вони користувалися тими самими правилами, що й нині, але сформульованими словесно.

У Стародавній Греції вимірюванням площ цікавився Евклід.

Знайдено деякі рукописи, створені на Русі, зокрема збереглася копія рукопису „О земном верстании, как землю верстать”. Дуже цікаві формули є у ньому. Але є також багато неточностей. Користуючись цими формулами, у 1560 р. побудували храм Василя Бліженого в Москві. Як бачимо, й у ті часи застосовували знання з геометрії на практиці.

А ми продовжимо подорож.

Станція „Практична”

Учитель. Уже недалеко залишилося до нашого міста. Виконана письмова робота (умови завдань записано & картках) буде перепусткою до нього. Задачі 1 і 2 розв'яжіть, виконавши необхідні вимірювання. Перемальовувати малюнки не треба.

1-й варіант

 1. Знайти площі заштрихованих частин фігур.

2. Знайти площу фігури ABCDE

3. Площа паралелограма дорівнює 96м², а його висоти – 6 м і 8 м. Обчислити периметр паралелограма.

2-й варіант

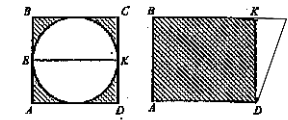1. Знайти площі заштрихованих частин фігурі

2. Знайти площу фігури ABCDE

3. Діагоналі ромба відносяться як 3:4, а йот сторона дорівнює 25 см. Обчислити площу ромба.

Учитель. Ми потрапили в місто Площеград. Результати подорожі будуть оголошені на наступному уроці. Удома вам треба виконати такі завдання.

1. Скласти дві задачі на обчислення площі та роз в'язати їх.

2. Повторити формули для обчислення площ фігур.

Подорож закінчу словами математика Олексія Миколайовича Крилова: „Рано чи пізно будь-яка правильна математична ідея знаходить застосування в тій чи іншій справі. Завтра математика стане ще могутнішою, ще важливішою і потрібнішою для людей, ніж сьогодні”

 

 

УРОК – СЛІДСТВО У 9 КЛАСІ

Тема: Чотирикутники.

Мета уроку: закріплення та систематизація знань учнів з теми; активізація діяльності учнів у ході навчання; підвищення інтересу учнів до вивчення предмета.

Обладнання і оформлення уроку: картки-креслення завдань; аудіо-магнітофон із записом музики до телефільму «Пригоди Шерлока Холмса і доктора Ватсона».

Форма проведення уроку: гра „Слідство ведуть знавці геометрії”.

Звучить музика. Вчитель зачитує план слідчо-пошукових заходів.

Етапи уроку (план слідчо-пошукових заходів)

•                     Формування слідчих груп.

•                     Встановлення осіб, укладання орієнтирів.

•                     Складання фотороботів.

•                     Експертиза речових доказів.

•                     Винесення звинувачення та його доведення.

•                     Підбиття підсумків слідчо-пошукових заходів.

•                     Повідомлення домашнього завдання.

 

ХІД УРОКУ

1. Формування слідчих груп

Учитель. Увага! У місті Чотирикутники відбулася низка надзвичайних подій. Розкрити їх зможуть лише справжні знавці геометрії. У зв'язку з надзвичайним станом у місті створено загін щодо боротьби з помилками і хуліганством. Загін складається з п'яти слідчих груп, яким належить провести слідчо-пошукові заходи з метою відновлення в місті геометричного правопорядку.

Клас розподіляється на 5 груп, які займають свої місця.

2. Встановлення осіб, укладання орієнтирів

Учитель. Слідство має свідчення очевидців, за якими необхідно встановити особи підозрюваних. Прошу слідчі групи записати свої версії.

•                     В одного з чотирикутників довжини всіх сторін однакові, а довжини діагоналей різні.

•                     У другого чотирикутника дві протилежні сторони паралельні, а дві інші – ні.

•                     У третього – протилежні сторони попарно паралельні, а діагоналі мають різну довжину й не перпендикулярні одна до одної.

•                     У четвертого – всі кути прямі, а діагоналі не перпендикулярні.

•                     У п'ятого – всі кути однакові й усі сторони однакові.

Учасники гри слухають версії слідчих груп щодо „осіб”, підозрюваних у порушеннях правопорядку (ромб, трапеція, паралелограм, прямокутник, квадрат). Кожна із груп отримує завдання вести „справу” одного з чотирикутників.

Завдання групам. Укласти орієнтири для розшуку за формою: назва чотирикутника, що розшукується, його означення, особливі прикмети (властивості).

3. Складання фотороботів

Учитель. До роботи залучаються криміналісти. Треба за відомими даними скласти фотороботи чотирикутників, що знаходяться в розшуку.

Кожна група отримує альбомний аркуш з даними, на якому необхідно розв'язати задачу на побудову.

ABCD – паралелограм		MNOP – рівнобедрена трапеція
ABKD – ромб	KEOF – прямокутник		PRST – квадрат

 

Після завершення роботи аркуші з готовими кресленнями вивішують на дошку під заголовком „Їх розшукують знавці”. Групи усно доповідають про шлях побудови.

4. Експертиза речових доказів

Групи одержують завдання: за готовими рисунками сформулювати оперативну задачу і розв'язати її, керуючись законами геометрії.

ABCD – паралелограм,		EKBM – трапеція, P=50 см (периметр)
	P=60 см S=? (площа)		HZ=8 см S=? (площа)

Після обговорення один із членів групи біля дошки усно формулює умову і розв'язує задачу. Члени інших груп можуть доповнювати відповідь і пропонувати інші способи розв'язання.

5. Винесення звинувачування та його доведення

На цьому етапі уроку учні формулюють і доводять властивості чотирикутників за готовими рисунками. (Бажано, щоб відповідали найменш активні учні, а всі інші члени груп доповнювали відповіді.)

6. Підбиття підсумків слідчо-пошукових заходів

Учитель. Адміністрація міста висловлює подяку слідчим групам за роботу з установлення в місті Чотирикутники геометричного правопорядку і сподівається на подальшу плідну співпрацю. За відмінну роботу оголошується подяка з відзнакою в журналі... (йде перелік прізвищ учнів). Роботу решти членів групи прошу оцінити самостійно і подати списки оцінок. Удома вам належить провести аналітичну роботу за планом: вирізати з паперу паралелограм, ромб, трапецію і придумати, як розрізати на частини кожну з цих фігур, щоб при цьому з них можна було скласти прямокутник; поміркувати, які виміри необхідно зробити, щоб обчислити площу кожної з цих фігур