Орієнтовні варіанти інтегрованих контрольних робіт з математики для ДПА
Для підготовки до ДПА з математики.
Учень 9 класу має бути готовий до здачі ДПА з математики, і даний посібник допоможе йому усвідомити суть завдань і їх тип.

Підготував
вчитель математики
Розтоцької ЗОШ
І-ІІ ступенів
Бобрик Василь Вікторович
РОЗТОКИ – 2017
Пояснювальна записка
Збірник призначений для проведення державної підсумкової атестації з математики в дев'ятих класах загальноосвітніх навчальних закладів.
Зміст завдань відповідає чинній програмі для загальноосвітніх навчальних закладів та програмі для шкіл.
Посібник «Збірник завдань на державну підсумкову атестацію з математики (9 клас)» містить 10 варіантів інтегрованих контрольних робіт з алгебри та геометрії. Кожен варіант атестаційної роботи складається з трьох частин, які відрізняються за складністю та формою тестових завдань.
ДПА з математики проводиться протягом 3 академічних годин – 135 хв.
Список використаних джерел
- Бурда М. І. Збірник завдань для державної підсумкової атестації з алгебри. 9 клас/ М.І.Бурда , О.Я. Біляніна , О. П. Вашуленко. – Харків: Гімназія, 2008.– 224 с.
- Істер О.С. Збірник завдань для державної підсумкової атестації з математики: 9 клас/ О.С. Істер, О.І. Глобін, О.В. Комаренко. –2-ге вид., доопрац. – К. : Центр навч.-метод. л-ри, 2012.– 112 с.:іл.
- Мерзляк А.Г. Збірник завдань для державної підсумкової атестації з математики: 9-ий клас/ А.Г. Мерзляк, В.Б.Полонський, М.С. Якір; за ред. М.І. Бурди. – К.: Центр навч.-метод. л-ри, 2014.– 256 с.
- Істер О.С. Збірник завдань для атестаційних письмових робіт з математики: для загальноосвітніх навчальних закладів.: 9-й кл. / О.С. Істер, О. В. Єргіна. – Київ: Генеза, 2015.– 32 с.:іл.
Структура, зміст та оцінювання завдань атестаційної роботи
У першій частині атестаційної роботи пропонується 12 завдань з вибором однієї правильної відповіді (8 завдань з алгебри і 4 завдання з геометрії). Для кожного тестового завдання з вибором відповіді подано чотири варіанти відповіді, з яких тільки один правильний. Завдання з вибором відповіді вважається виконаним правильно, якщо в бланку відповідей указана тільки одна літера, якою позначена правильна. При цьому учень не повинен наводити будь-які міркування, що пояснюють його вибір.
Правильне розв'язання кожного завдання цього блоку № 1.1—1.12 оцінюється одним балом. Якщо ж указана учнем відповідь є неправильною, то виконання завдання оцінюється у 0 балів.
Друга частина атестаційної роботи складається із 5 завдань (3 завдання з алгебри і 2 завдання з геометрії) відкритої форми з короткою відповіддю. Таке завдання вважається виконаним правильно, якщо в бланку відповідей записана правильна відповідь (наприклад, число, вираз, корені рівняння тощо). Усі необхідні обчислення, перетворення тощо учні виконують на чернетках.
Правильне розв'язання кожного із завдань № 2.1—2.5 цього блоку оцінюється двома балами, а якщо відповідь є неправильною – 0 балів.
Третя частина атестаційної роботи складається з 3 завдань (2 завдання з алгебри і 1 завдання з геометрії відкритої форми з розгорнутою відповіддю. Завдання третьої частини вважаються виконаними правильно, якщо учень навів розгорнутий запис розв'язування завдання з обґрунтуванням кожного етапу та дав правильну відповідь. Завдання третьої частини атестаційної роботи учні виконують на аркушах зі штампом відповідного загальноосвітнього навчального закладу. Формулювання завдань третьої частини учень не переписує, а вказує тільки номер завдання.
Правильність виконання завдань третьої частини оцінює вчитель відповідно до критеріїв і схеми оцінювання завдань. Правильне розв'язання завдання № 3.1—3.3 оцінюється у чотири бали.
Виправлення і закреслення в оформленні розв’язання завдань третьої частини, якщо вони зроблені акуратно, не є підставою для зниження оцінки.
Для оцінювання в балах завдань третьої частини атестаційної роботи пропонується користуватися критеріями, наведеними у таблиці:
|
Що виконав учень |
Відповідна к-сть балів |
|
Максимальний бал – 4 |
|
|
Отримав правильну відповідь і навів повне її обґрунтування |
4 бали |
|
Отримав правильну відповідь, але не достатньо обґрунтовано |
3 бали |
|
Отримав правильну відповідь, записав хід розв’язування, але в процесі розв’язування припустився помилки обчислювального або логічного характеру. |
|
|
Суттєво наблизився до правильного результату або знайшов лише частину правильної відповіді. |
2 бали |
|
Розпочав розв’язувати завдання правильно, але в процесі розв’язання допустився помилки у застосуванні необхідного твердження чи формули. |
1 бал |
|
Розпочав неправильно, але наступні етапи розв’язання виконав правильно. |
|
|
Розв’язання не відповідає жодному з наведених вище критеріїв |
0 балів |
Наведені критерії мають бути відомі учням.
Відповідність кількості набраних балів учнем загальноосвітнього класу оцінці за 12-бальною системою оцінювання навчальних досягнень учнів наведено у таблиці .
|
Кількість набраних балів |
Оцінка за 12-бальною системою оцінювання навчальних досягнень учнів |
|
1—2 |
1 |
|
3—4 |
2 |
|
5—7 |
3 |
|
8—10 |
4 |
|
11—12 |
5 |
|
13—15 |
6 |
|
16—18 |
7 |
|
19—22 |
8 |
|
23—25 |
9 |
|
26—28 |
10 |
|
29—31 |
11 |
|
32—34 |
12 |
Варіант 1
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
-
Спростіть вираз
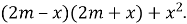
-
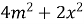 Б)
Б) 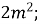 B)
B) 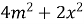 ; Г)
; Г) 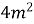 .
.
-
Виконайте дію
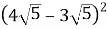 ?
?
-
Виконайте дію
А) ![]() ; Б)
; Б) ![]() ; В) 5; Г) 20.
; В) 5; Г) 20.
- Скільки кілограмів сушених слив отримають з 8 кг свіжих, якщо з 10 кг свіжих слив отримали 1,5 кг сушених?
А) 1,1 кг; Б) 1,2 кг; В) 0,8 кг; Г) 1,4 кг.
-
Обчисліть:
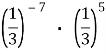 .
.
-
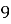
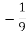 ; B)
; B) 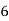
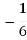 .
.
-
Розв'яжіть нерівність
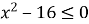 .
.
-
Розв'яжіть нерівність
-
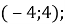 Б)
Б) 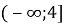 ; В)
; В) 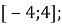 Г)
Г) 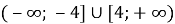 .
.
- На одній половині шахівниці кожен білий квадрат зафарбували у зелений колір. Яку частину від усіх квадратів шахівниці становитимуть зелені квадрати?
-
 ; Б)
; Б)  ; В)
; В)  ; Г)
; Г) 
- У ящику є 20 кульок, пронумерованих від 1 до 20. Навмання витягують одну кульку з них . Яка ймовірність того , що її номер є кратним числу 7?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
- Укажіть коренем якого рівняння є число -13 ?
-
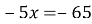
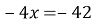
Б) ![]()
![]()
- Знайдіть координати середини відрізка QP, якщо Q(-1;3), а P(5; -11).
-
(-2; 4) Б) (-2; -4) В) (2; -4) Г ) (2; 4)
-
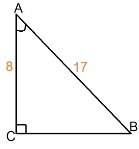 Знайдіть
Знайдіть 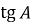 .
.
-
-
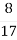 ; Б)
; Б)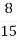 ; В)
; В) 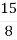 ; Г)
; Г) 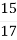 .
.
- У квадрат зі стороною 10 см вписано круг. Яка площа цього круга?
-
5 см2; Б) 5


-
Які координати матиме точка А(-2; 0) при паралельному перенесенні :
 ?
?
-
Які координати матиме точка А(-2; 0) при паралельному перенесенні :
-
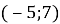
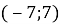
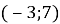
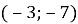
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
-
Спростіть вираз
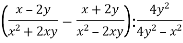 ?
?
-
Знайдіть найменше ціле значення
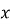
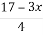 і
і 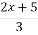 є від’ємною.
є від’ємною.
-
Знайдіть область значень функції
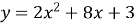 .
.
-
При яких значеннях
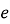
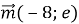 і
і 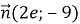 будуть колінеарні ?
будуть колінеарні ?
- Знайдіть площу прямокутної трапеції з основами 10 см і 18 см, якщо її більша бічна сторона утворює з більшою основою кут 300.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обгрунтування . У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
- Знайдіть 5 послідовних парних натуральних чисел, коли відомо, що сума квадратів перших трьох чисел дорівнює сумі квадратів двох останніх.
-
Розв’яжіть систему рівнянь
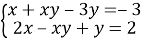
-
Кути паралелограма відносяться як 4:5. Знайдіть кут між висотами паралелограма, проведеними із вершини тупого кута.
Варіант 2
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
-
Укажіть число , що є коренем рівняння
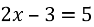
![]()
![]()
![]()
-
Яку відстань долає автомобіль за
 год, якщо його швидкість – 75 км/год ?
год, якщо його швидкість – 75 км/год ?
А) ![]()
![]()
![]()
-
Перетворити вираз
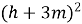
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
-
Укажіть точку через яку проходить пряма
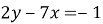
-
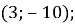 Б)
Б)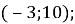 B)
B) 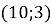
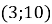
-
Знайти значення виразу
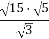 .
.
-
Знайти значення виразу
-
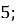
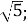 В)
В)

-
Виконайте піднесення до степеня

-
Виконайте піднесення до степеня
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г)![]() .
.
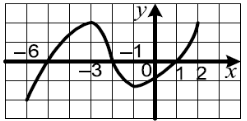
- Укажіть область значень функції визначеної на проміжку [-6; 2].
![]()
![]()
![]()
![]()
-
У геометричній прогресії
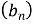
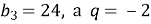 . Знайдіть
. Знайдіть 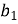 .
.
-
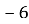
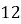
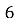
- Точка C належить відрізку АВ. Довжина АВ=12 см, а ВC=3,7 см. Знайти АC.
-
9 см; Б) 9,3 см; В) 8,3 см; Г ) 8,7 см.
- Діагональ ромба утворює з його стороною кут 550. Знайти менший кут ромба.
-
1100 ; Б) 600 ; В) 800 ; Г) 700.
-
Яка площа трикутника, у якого дві сторони дорівнюють 8 см і 17 см, а кут між ними
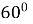 ?
?
-
Яка площа трикутника, у якого дві сторони дорівнюють 8 см і 17 см, а кут між ними
-
136 см2; Б) 34
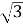 см2; В) 68 см2; Г)
см2; В) 68 см2; Г)  см2.
см2.
-
При якому значенні
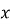
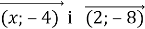 ?
?
-
При якому значенні
- 1 ; Б) -16 ; В) 0; Г) 16 .
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
-
Виконайте віднімання:
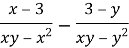 .
.
-
Розв’яжіть систему рівнянь
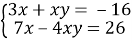 .
.
-
Один із коренів рівняння
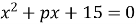 дорівнює -5. Знайти p і другий корінь цього рівняння.
дорівнює -5. Знайти p і другий корінь цього рівняння.
-
Вершинами трикутника є точки R(-3;1), S(2;-2) і T(-4;6). Знайдіть медіану RМ
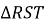
-
У трикутнику АВС
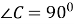 ,
, 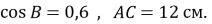 Знайти периметр цього трикутника.
Знайти периметр цього трикутника.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обгрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
- Потяг, який затримався на 1 год, ліквідував запізнення на перегоні завдовжки 300 км, збільшивши швидкість на 10 км/год. Знайдіть, за який час потяг мав подолати цей перегін з початковою швидкістю.
-
Знайти область визначення функції:
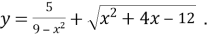
- Діагональ рівнобічної трапеції ділить її тупий кут навпіл, а середню лінію ділить на відрізки 4 см і 5 см. Знайдіть периметр даної трапеції.
Варіант 3
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
-
Розв’яжіть нерівність
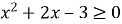 .
.
![]() ; Б)
; Б) ![]() ; B)
; B) ![]() ; Г)
; Г) ![]()
- Сплав містить 35% алюмінію. Скільки алюмінію міститься у 60 кг сплаву?
А) 1,7 кг; Б) 12 кг; В) 20 кг; Г) 21 кг.
-
Перетворіть вираз
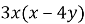
А) ![]()
![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
-
Укажіть точку перетину графіка прямої
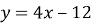
![]()
![]()
![]() Г)
Г) ![]()
- Яке число треба підставити замість зірочки, щоб число 1*45 було кратне 9 ?
![]()
![]()
![]()
![]()
-
Дано арифметичну прогресію, у якої
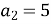 , а
, а 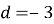
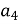 .
.
![]()
![]()
![]()
![]()
-
Знайти значення виразу
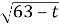 , якщо
, якщо 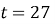
![]()
![]()
![]()
![]()
-
Розв’язати рівняння
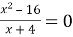 .
.
![]()
![]()
![]()
- Сторони квадрата становить 2 см. Знайти його діагональ.
А) 8 см; Б) 4 см; В) ![]() ; Г)
; Г) ![]()
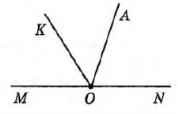
-
На малюку
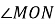
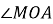
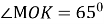 . Тоді
. Тоді 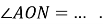
А) 650; Б) 500; В) неможливо визначити; Г) 1300.
- Периметр рівнобічної трапеції 26 см, а її бічна сторона становить 7 см. Яка довжина середньої лінії цієї трапеції?
![]()
![]()
![]()
- Знайти площу ромба зі стороною 8 см і кутом 600.
А) ![]() ; Б) 32 см2; В) 64
; Б) 32 см2; В) 64![]() см2; Г)
см2; Г) ![]() .
.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
-
Спростіть вираз
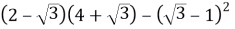 .
.
-
Розв'яжіть нерівність
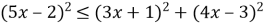 .
.
-
На якому проміжку функція
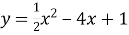 буде зростати ?
буде зростати ?
- У рівносторонній трикутник зі стороною 5 см вписано сполученням середин його сторін новий трикутник; у цей трикутник таким самим способом вписано новий трикутник – і так далі до нескінченності. Знайдіть суму периметрів усіх вписаних трикутників.
- Одна сторона трикутника на 5 см більша за другу, а кут між ними 600. Знайдіть периметр трикутника, якщо його третя сторона становить 7 см.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обгрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
- На одному верстаті треба обробити 90 деталей, а на другому – 100. За одну годину перший верстат обробляє на 5 деталей більше. Скільки деталей обробляється на першому верстаті за годину, якщо його роботу закінчено на 1 год раніше, ніж роботу другого верстата ?
-
Розв’яжіть систему рівнянь
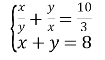 .
.
- Доведіть, що чотирикутник АВСD з вершинами в точках А(2;-2), В(1;2), С(-3;1), D(-2; -3) є прямокутником.
Варіант 4
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
-
Знайдіть значення виразу
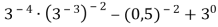 .
.
![]()
![]()
![]()
-
Розв'язати рівняння
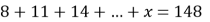
А) 10 ; Б) 152; В) 29; Г) ![]()
- Чому дорівнює НСД чисел 12 і 16 ?
А) ![]()
![]()
![]()
![]()
-
На якому з рисунків зображено графік функції
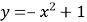 ?
?
- Знайдіть відсотковий вміст міді у сплаві, якщо 40 т сплаву містить 5 т міді.
- 8%; Б) 87,5% ; В)92%; Г) 12,5%.
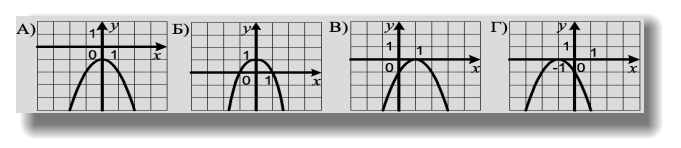
- Запишіть число 780 000 000 у стандартному вигляді.
-
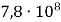 ; Б)
; Б) 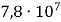 ; В)
; В) 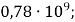 Г)
Г) 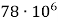 .
.
- Аліна і Ангеліна виготовляли листівки. Листівки, зроблені Ангеліною, відносяться до листівок, зроблених Аліною, як 3:5 . Яку частину від усіх листівок виготовила Аліна?
-
 ; Б)
; Б)  ; В)
; В)  ; Г )
; Г )  .
.
-
Скільки різних коренів має рівняння
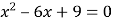 ?
?
-
Скільки різних коренів має рівняння
![]()
![]()
![]()
![]()
- Знайдіть площу трикутника зі сторонами 3 м, 4 м і 5 м.
-
12 м2; Б) 6 м2; В) 10 м2 ; Г) 7,5 м2.
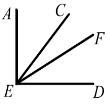
- З вершини прямого кута АЕD проведено два промені EC і EF так, що кут AEF=470, кут CED=520. Знайти величину кута CEF.
-
50 ; Б) 430 ; В) 90 ; Г) 380.
-
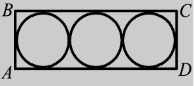 У прямокутнику АВСD вписано три рівних кола радіуса 2 см так, як показано на рисунку. Яка площа прямокутника АВСD ?
У прямокутнику АВСD вписано три рівних кола радіуса 2 см так, як показано на рисунку. Яка площа прямокутника АВСD ?
-
А) 24 см2 Б) 12 см2 В) 48 см2 Г) 64 см2 .
-
Знайдіть координати точки перетину прямих
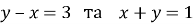
-
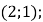 Б)
Б) 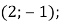 Б)
Б) 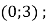
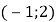
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
-
Чому дорівнює значення виразу
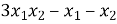 , де
, де 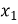 і
і 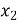 ─ корені рівняння
─ корені рівняння 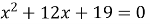 ?
?
-
Розв’яжіть систему рівнянь
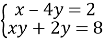
- У бригаді було 5 робітників, середній вік яких становив 35 років. Після того як бригада поповнилася одним робітником, середній вік робітників бригади став 34 роки. Скільки років робітнику, який поповнив бригаду?
- Довжини сторін багатокутника утворюють арифметичну прогресію, різниця якої дорівнює 3 см. Найбільша сторона багатокутника дорівнює 38 см. Знайдіть кількість сторін багатокутника, якщо його периметр дорівнює 258 см.
-
Дано вектори
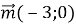 і
і 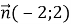 . Знайдіть міру кута між векторами
. Знайдіть міру кута між векторами 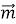 і
і 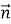 .
.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
- Для перевезення 60 т вантажу було замовлено певну кількість вантажівок. Але на кожну було навантажено на 1 т більше, ніж планувалося, тому дві виявилися зайвими. Скільки вантажівок було використано?
- Знайдіть область допустимих значень функції:
![]() .
.
-
Гіпотенуза і катет прямокутного трикутника відповідно дорівнюють 10 см і 6 см. Знайдіть довжину найбільшої сторони подібного йому трикутника, площа якого дорівнює 216 см2.
Варіант 5
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
- Відрізок 5дм 7см зменшили на 27 см. Яка довжина утвореного відрізка? А) 31 см; Б) 3 дм; В) 20 см; Г) 480 см.
1.2. Спростіть вираз (3а + 5) - (2 - а).
А) 4а + 3; Б) 2а + 3; В) 4а + 7; Г) 2а + 7.
1.3.Чому дорівнює значення виразу ![]() ?
?
А) 1; Б) 5; В) ![]() ; Г)
; Г) ![]() .
.
1.4.Чому дорівнює сума п’яти перших членів геометричної прогресії , перший член якої ![]() =6, а знаменник q=2?
=6, а знаменник q=2?
А) 182; Б) 186; В) -4; Г) -3.
1.5. Подайте у вигляді дробу вираз ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.6. У кожному купе вагону поїзда 4 місця. Який номер купе, де їде пасажир, номер місця якого 17?
А) 4 ; Б) 5 ; В) 6; Г) 7 .
1.7. Областю визначення якого з даних виразів є множина дійсних чисел? А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.8. У кошику 12 червоних яблук, 7 зелених і 5 жовтих. Яка ймовірність того, що навмання взяте яблуко буде не червоним ?
А) 0,292; Б) 0,208; В) 0,5; Г) 0,714.
1.9. Прямокутник розмірами 2,4 см × 3 см розрізали на квадратики зі стороною 0,6 см. Скільки квадратиків утворилося ?
А) 20; Б) 30; В) 10; Г) 18.
1.10. Як можна закінчити речення «У будь - якій трапеції…», щоб утворилося правильне твердження.
А) діагоналі точкою перетину діляться навпіл;
Б) діагоналі рівні; В) дві сторони рівні; Г) дві сторони паралельні.
1.11. У коло вписано квадрат зі стороною ![]() . Знайдіть сторону правильного трикутника, описаного навколо цього кола.
. Знайдіть сторону правильного трикутника, описаного навколо цього кола.
А) ![]() см ; Б)
см ; Б) ![]() см ; В)
см ; В) ![]() см; Г)
см; Г) ![]() см
см
1.12. Чому дорівнює площа паралелограма, сторони якого дорівнюють 4 см і 6 см, а кут між ними становить ![]() ?
?
А)![]() ; Б)
; Б)![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
2.1. Знайдіть перший член арифметичної прогресії (![]() ), якщо
), якщо ![]() = 17,
= 17, ![]() = 47?
= 47?
2.2.Розвяжіть рівняння ![]() .
.
2.3.Знайдіть медіану і середнє значення вибірки 3,2; 3,5; 4,3; 4,8 ; 5; 5,6.
- У рівносторонній трикутник зі стороною 4 см вписано сполученням середин його сторін новий трикутник; у цей трикутник таким самим способом вписано новий трикутник – і так далі до нескінченності. Знайдіть суму периметрів усіх вписаних трикутників.
2.5. Знайдіть периметр прямокутного трикутника, гіпотенуза якого дорівнює 13 см, а один із катетів на 7 см більший за інший.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
3.2. Катер пройшов 10 км за течією річки і 9 км по озеру , витративши на весь шлях одну годину. Знайдіть власну швидкість катера , якщо швидкість течії річки становить 2 км/год.
3.2. Розв’яжіть графічно рівняння ![]() .
.
3.3. Основи рівнобічної трапеції дорівнюють 10 см і 8 см. Знайдіть висоту трапеції, якщо її діагональ перпендикулярна до бічної сторони.
Варіант 6
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
- Знайдіть значення виразу: 0,5а + b при а = -1,2, b = 2.
А) 1,4; Б) -1,4; В) -2,6; Г) 2,6.
1.2. Скоротіть дріб ![]() .
.
А)![]() ; Б)
; Б)![]() ; В)
; В)![]() ; Г)
; Г)![]() .
.
1.3. Яка область визначення функції y =![]() ?
?
А) (-![]() ; 3]; Б) [3; +∞); В) (3; +∞) ; Г) (-∞;3).
; 3]; Б) [3; +∞); В) (3; +∞) ; Г) (-∞;3).
1.4. Коренем якого з рівнянь є число 2?
А) 6х = 3; Б) х – 4 = 0; В) ![]() = х - 5; Г) 2х + 7 = 11.
= х - 5; Г) 2х + 7 = 11.
1.5. Спростіть вираз 3![]() - 8
- 8![]() .
.
А) 10![]() ; Б) 4
; Б) 4![]() ; В) 26
; В) 26![]() ; Г)9
; Г)9![]() .
.
1.6.Чому дорівнює сума коренів рівняння х2 – 21х – 10 = 0?
 А)21; Б) -21; В) 10; Г) -10.
А)21; Б) -21; В) 10; Г) -10.
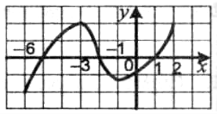
1.7. Укажіть проміжок спадання функції, визначеної на проміжку [- 6; 2], графік якої зображено на рисунку.
А)[-5; -3]; Б) [-3; -1] В) [-2; 1] Г) [-3; -2].
1.8. У яких координатних кутах лежить графік функції ![]() ?
?
А) І і ІІ; Б) І і ІІІ; В. ІІ і ІV ; Г) II і ІІІ.
1.9. Сума кутів опуклого многокутника дорівнює 1700°. Чому дорівнює кількість його сторін?
А)8; Б)10; В)12; Г) такий многокутник не існує.
1.10. Обчисліть площу паралелограма, дві сторони якого дорівнюють 6 см і 5![]() см, а кут між ними – 45°.
см, а кут між ними – 45°.
А)30 см²; Б) 15 см²; В)30![]() см²; Г ) 15
см²; Г ) 15![]() см².
см².
1.11.Сторони трикутника відносяться як 7 : 6 : 4. Знайдіть більшу сторону подібного йому трикутника, менша сторона якого дорівнює 12 см.
А) 84 см; Б)56 см; В) 14 см; Г) 21 см.
1.12. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу дорівнює 3 см, а гіпотенуза – 27 см.
А) 81 см; Б) 9 см; В) 3 см; Г) 24 см.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
2.1. Знайдіть номер члена арифметичної прогресії 11,8; 12,4; 13; …, який дорівнює 20,8.
2.2. Розв’яжіть нерівність ![]()
2.3. До 8 кг 60-відсоткового розчину солі додали 4 кг води. Яким після цього став вміст солі в розчині?
2.4. Катети прямокутного трикутника дорівнюють 5 см і 6 см. Знайдіть довжину медіани трикутника, проведеної до більшого катета.
2.5. З точки до прямої проведено дві похилі, проекції яких на пряму дорівнюють 5 см і 9 см . Знайдіть відстань від даної точки до цієї прямої, якщо одна з похилих на 2 см більша за другу.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Моторний човен пройшов 6 км проти течії річки і 8 км за течією, витративши на весь шлях 1 год. Яка швидкість човна в стоячій воді, якщо швидкість течії річки становить 2 км/год?
3.2. Побудуйте графік функції ![]() . Користуючись графіком знайдіть:
. Користуючись графіком знайдіть:
1) область значень функції;
2) при яких значеннях х функція набуває додатних значень.
3.3.Основи рівнобічної трапеції дорівнюють 15 см і 33 см, а діагональ ділить гострий кут навпіл. Знайти площу трапеції.
Варіант 7
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
1.1.Обчисліть значення виразу (-2,16-4,24):(-16) .
А) 0,4; Б)-0,4; В) -4; Г) 4.
1.2. Якому одночлену дорівнює вираз ![]() ?
?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.3.Розвяжіть нерівність -3x+26≥23.
А) x≤1; Б) x≥-1; В) x≤-1 ; Г) x≥1.
1.4. Знайдіть координати точки перетини графіка рівняння 6х- 7у=42 з віссю абсцис.
А)(0;7); Б)(-6;0); В)(0;-6); Г(7;0).
1.5.Чому дорівнює добуток коренів рівняння х²-2х-5=0?
А) -5; Б)-2; В) 2; Г)5.
1.6.Знайдіть сьомий член арифметичної прогресії, перший член якої дорівнює 8, а різниця дорівнює 0,5.
А)11; Б) 10; В) 10,5; Г) 9,5.
1.7. Розв’яжіть рівняння ![]() .
.
А)5; Б) -5; В) -5;5; Г) коренів немає.
1.8. У партії із 2000 деталей є 8 бракованих. Яка імовірність того, що навмання взята деталь буде бракованою ?
А) 0,4%; Б) 4%; В) 40%; Г) 0,5%.
1.9. Катети прямокутного трикутника дорівнюють 2 см і ![]() см. Знайдіть синус більшого гострого кута цього трикутника.
см. Знайдіть синус більшого гострого кута цього трикутника.
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.10. Знайдіть радіус кола, описаного навколо трикутника, якщо![]() см, а кут
см, а кут ![]()
А) 6 см Б) 8см В) 8![]() Г) 16 см
Г) 16 см
1.11. При якому значенні a вектори ![]() перпендикулярні?
перпендикулярні?
А) 10; Б)-1; В)18; Г)-18.
1.12. Знайдіть більшу основу трапеції, якщо вона довша за іншу на 2 см, а середня лінія становить 10 см.
А) 11 см; Б) 9 см; В) 12 см; Г) 6 см.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
2.1.Чому дорівнює сума семи перших членів геометричної прогресії (bn), якщо b1 = 6, b6 = 192 ?
2.2.Розвяжіть систему рівнянь ![]()
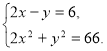
![]()
![]()
2.3.Знайдіть координати точок перетину кола x2 + y2 = 10 і прямої y = x – 2.
2.4. Діагоналі ромба дорівнюють 12 см і 16 см. Знайдіть периметр ромба.
2.5. У рівнобедреному трикутнику висота, проведена до бічної сторони, ділить її на відрізки 2 см і 8 см, рахуючи від вершини кута при основі. Знайдіть площу трикутника.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Катер проплив 48 км за течією річки і повернувся назад. На це він витратив 7 годин. Швидкість течії 2 км/год. Знайдіть власну швидкість катера.
3.2. Доведіть, що при всіх дійсних значеннях b виконується нерівність:
(2b – 8) (b – 2) +3 > (b – 3)2.
3.3. Точка перетину діагоналей рівнобічної трапеції віддалена від основ на 4 см і 7 см. Знайдіть площу трапеції, якщо її менша основа дорівнює 8 см.
Варіант 8
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
1.1.Обчисліть значення виразу: (–0,8 +3,8)3.
А) 81; Б)3; В) 9; Г) 27.
1.2. Спростіть вираз ![]()
А) 2,8a3b7; Б) –2,8a3b7 ; В) 28a4b7 ; Г) –2,8a2b12.
1.3. Графіком якої з функцій є гіпербола?
А) у = 2х+7; Б) у = ![]() ; В) у =
; В) у = ![]() ; Г) у = х²+7.
; Г) у = х²+7.
1.4. Областю визначення якої функції є проміжок (-∞;4)?
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.5. Чому дорівнює сума коренів рівняння х² + 9х – 2 = 0?
А) 2; Б)-2; В) 9; Г)-9.
1.6. Чому дорівнює значення виразу ![]() ?
?
А)5; Б) 6; В) 12; Г) 13.
1.7. Спростіть вираз![]() .
.
А) ![]() ; Б)
; Б) ![]() В) a + 6; Г) a – 6.
В) a + 6; Г) a – 6.
1.8. Скількома способами можна з цифр 1, 2, 3, 4, 5, 6 скласти трицифрове число, якщо цифри не повторюватимуться.
А) 6; Б) 720; В. 120; Г. 30.
1.9. Бічні сторони трапеції дорівнюють 3 см і 7 см. Знайдіть середню лінію трапеції, якщо в неї можна вписати коло.
А) 5 см; Б) 4 см; В) 6 см; Г) знайти неможливо.
1.10. Чому дорівнює площа круга, довжина кола якого 16![]()
А) 8![]()
![]()
![]()
![]()
1.11. Обчисліть скалярний добуток векторів ![]() .
.
А) 5; Б)6; В)-4; Г)-5.
1.12. Знайти об’єм прямокутного паралелепіпеда з розмірами: 50 см, 7 дм і 1,2 м.
А) 420 см3; Б) 4200 см3 В) 42 000 см3; Г) 420 000 см3 .
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
-
Складіть квадратне рівняння, корені якого дорівнюють
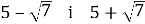
-
Спростіть вираз
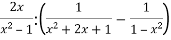
-
Розв’яжіть систему нерівностей
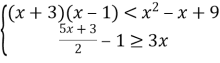 .
.
-
Знайдіть рівняння прямої, яка проходить через точку P(2;-5) і паралельна прямій

- Основи прямокутної трапеції дорівнюють 6 см і 12 см, а один із кутів трапеції дорівнює 300. Знайдіть площу трапеції.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Тракторист мав за певний час зорати поле площею 180 га . Проте щодня він зорював на 2 га більше, ніж планував, і закінчив роботу на 1день раніше, ніж планувалося. За скільки днів тракторист зорав поле?
3.2. Побудуйте графік функції у = – х² – 4х + 5. Користуючись графіком знайдіть:
1) область значень функції;
2) проміжок спадання функції.
3.3.Основи рівнобічної трапеції дорівнюють 9 см і 21 см, а діагональ – 17 см. Знайдіть радіус кола, описаного навколо даної трапеції.
Варіант 9
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
-
Порівняйте 24 хв і
 год.
год.
-
24 хв >
 год Б) не можна порівняти
год Б) не можна порівняти
-
В) 24 хв <
 год Г) 24 хв =
год Г) 24 хв =  год
год
1.2. Скільки коренів має рівняння 0 ⋅ x = ![]()
- Безліч Б) один В) жодного Г) два
1.3. Який вираз є квадратом одночлена 3х4y2?
- 6х8y4 Б) 9х8y4 В) 3х16y4 Г) 9х16y4
1.4. Знайдіть значення виразу (![]()
![]() 0.
0.
А) 2,5 Б) 1,75 В) 1,5 Г) 1,25
1.5. Спростіть вираз 6![]() –
– ![]()
А) 6![]() Б) 8
Б) 8![]() В) 4
В) 4![]() Г) 12
Г) 12![]()
1.6. Знайдіть координати вершини параболи y= x2 – 3x + 2.
А) (–1,5; 0,25) Б) (1,5; –0,25) В) (–1,5; –0,25) Г) (1,5; 0,25)
1.7. Довжина сторонни квадрата дорвінює ![]()
![]()
![]()
А) 8 <![]()
![]()
![]()
![]()
1.8. Стіл, початкова ціна якого становить 800 грн, двічі подорожчав, до того ж щоразу на 25%. Скільки тепер коштує стіл?
А) 1250 грн. Б) 1000 грн. В) 1200 грн . Г) 450 грн.
1.9. Кінці хорди кола ділять його на дві дуги, градусні міри яких відносяться як 1:17. Знайдіть градусну міру меншої дуги.
А) 40о Б) 80о В)10о Г) 20о
1.10. У паралелограмі АВСD проведено висоту ВМ до сторони АD. Обчисліть площу паралелограма, якщо ВС=8 см, ВМ=5 см.
А)40см²; Б) 20см²; В)13см²; Г ) 10см².
1.11. Знайти діаметр кола із довжиною 12,56 см.
А) 2 см Б) 3 см В) 4 см Г) 4,5 см
1.12. Знайдіть площу трикутника, одна зі сторін якого дорівнює 12 см, а висота, проведена до неї, – 5 см.
А) 60 см2 Б) 30 см2 В) 17 см2 Г) 20 см2
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
2.1. Обчисліть суму п’яти перших членів геометричної прогресії (bn), якщо b3 = 18, а знаменник q = 3.
2.2. Спростіть вираз ![]() .
.
2.3. Число 4 є коренем рівняння 3x2 – 8x + n = 0. Знайдіть другий корінь рівняння і значення n.
2.4. Знайдіть сторони прямокутника, якщо вони відносяться як 3:4 , а площа прямокутника становить 300 дм2.
2.5. Знайдіть периметр прямокутного трикутника, гіпотенуза якого на 7 см більша за один із катетів, а інший катет дорівнює 21 см.
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
3.1. За 2 футбольних і 4 волейбольних м’ячі заплатили 2000 грн. Після того як футбольний м’яч подешевшав на 20 %, а волейбольний подорожчав на 10 %, то за один футбольний і один волейбольний м’ячі заплатили 650 грн. Якою була початкова ціна кожного м’яча ?
- Розв’яжіть систему рівнянь:
![]()
- Сторони трикутника дорівнюють 8 см, 9 см і 13 см. Знайдіть медіану трикутника, проведену до його найбільшої сторони.
Варіант 10
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її до бланку відповідей.
- Яка числова нерівність є правильною?
А) 3031 < 3021; В) 44 371 > 44 381;
Б) 2529 > 2501; Г) 780 325 > 783 025.
1.2. Знайдіть різницю ![]()
А) ![]() ; Б)
; Б)![]() ; В)
; В)![]() ; Г)
; Г)![]() .
.
1.3. Подайте добуток (4+х)(х-4) у вигляді многочлена.
А) 16-![]() ; Б)
; Б) ![]() -16; В)
-16; В) ![]() -8; Г)
-8; Г) ![]() -4.
-4.
1.4. Подайте у вигляді квадрата двочлена вираз 9![]() 6аb+
6аb+![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В) (3а-b)(3а+b); Г)
; В) (3а-b)(3а+b); Г) ![]() .
.
1.5. Знайдіть дискримінант квадратного рівняння 2![]() -3х+1=0.
-3х+1=0.
А) ![]() ; Б) 1; В) -1; Г) 0.
; Б) 1; В) -1; Г) 0.
1.6. Яке число є кратним числу 24?
А) 2; Б) 72; В) 6; Г) 12.
1.7. Знайдіть координати вершини параболи у=![]() -2х-3.
-2х-3.
А) (-4;1); Б) (-1;0); В) (0;-1); Г) (1;-4).
1.8. Десять автобусних зупинок розташовані на прямій вулиці так, що відстані між будь-якими сусідніми зупинками однакові. Відстань між першою і третьою зупинками дорівнює 1,2 км. Яка відстань між першою і останьою зупинками.
![]()
![]()
![]()
![]()
1.9. Радіус кола дорівнює 2![]() см. Знайдіть сторону правильного трикутника,
см. Знайдіть сторону правильного трикутника,
описаного навколо цього кола.
А) 12 см; Б) 6 см; В) 6![]() см; Г) 3
см; Г) 3![]() .
.
1.10. Запишіть рівняння кола з центром у точці О(-2;1) та радіусом, що дорівнює
4.
А)![]() +
+![]() = 16; В)
= 16; В) ![]() +
+![]() = 16;
= 16;
Б) ![]() +
+![]() = 4; Г)
= 4; Г) ![]() +
+![]() = 16.
= 16.
1.11. Сторона прямокутника дорівнює 16 см і 12 см. Знайдіть довжину
діагоналей прямокутника.
А) 20 см; Б) 40 см; В) 4![]() ; Г) 2
; Г) 2![]() .
.
1.12. Які координати матиме точка ( -3; 0) при повороті на 900 проти годинникової стрілки ?
А) (0; 3); Б) (-3;3) ; В) (0; -3); Г) (3; 0).
Частина друга
Розв’яжіть завдання 2.1 – 2.6. Запишіть відповідь у бланк відповідей
2.1.Знайдіть суму всіх натуральних чисел, які менші за 250 і кратні числу 3.
2.2.Розвяжіть рівняння ![]() .
.
2.3. Знайдіть значення виразу ![]() .
.
2.4. Сторони трикутника дорівнюють 25 см, 29 см, 36 см. Знайдіть радіус описаного кола даного трикутника.
2.5.Чому дорівнює кут BAD чотирикутника ABCD, вписаного в коло, якщо ![]() ?
?
Частина третя
Розв’язання задач 3.1 – 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, то проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Двоє трактористів можуть зорати поле, працюючи разом, за 6 год. Одному з них, щоб зорати ![]() поля потрібно на 4 год більше часу, ніж іншому для того, аби зорати
поля потрібно на 4 год більше часу, ніж іншому для того, аби зорати ![]() поля. За скільки часу кожен із них самостійно зоре все поле ?
поля. За скільки часу кожен із них самостійно зоре все поле ?
3.2.При яких значеннях а і с вершина параболи ![]() знаходиться в точці А( -2;3).
знаходиться в точці А( -2;3).
3.3. Висота рівнобедреного трикутника, проведена до основи, дорівнює
20 см, а висота, проведена до бічної сторони, - 24 см. Знайдіть
площу цього трикутника.
|
ДПА | Математика 2017/2018 н.р. |
9 клас |


про публікацію авторської розробки
Додати розробку
