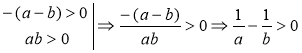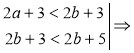Основні властивості числових нерівностей.

Тема уроку. Основні властивості числових нерівностей.

Мета уроку: домогтися засвоєння учнями змісту основних властивос­тей числових нерівностей та їхніх наслідків, а також способу доведення цих властивостей. Виробити вміння: відтворювати зміст вивчених властивостей, наслідків із них і їх доведення; застосовувати властивості числових нерівностей та наслідки з них для розв'язування вправ на порівняння буквених виразів та на доведення відповідних нерівностей.

Тип уроку: засвоєння знань, вироблення первинних умінь.

Наочність та обладнання: опорний конспект.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Учні виконують самостійну роботу № 1 [8].

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів

На цьому етапі уроку доречним буде слово вчителя про те, що:

• вивчення будь-якого математичного поняття включає в себе ви­вчення означення, властивостей та ознак цього поняття (якщо такі існують), а також питання про зв'язок поняття, що ви­вчається, із вивченим раніше матеріалом;
• незважаючи на досить велику зовнішню відмінність, що існує між рівностями і нерівностями, вони мають дуже багато спіль­них властивостей (у цьому місті доречно буде продемонструва­ти кілька найпростіших прикладів з числовими рівностями та відповідними числовими нерівностями), але при цьому мають суттєві відмінні властивості (також можна навести кілька при­кладів з числовими рівностями та нерівностями).

Тому цілком логічно буде сформулювати завдання на урок як вивчення властивостей числових нерівностей (через їх порівняння з відповідними властивостями числових рівностей); доведення цих властивостей із використанням вивченого на попередніх уроках означення, а також опанування учнями прийомів застосування доведених властивостей для розв'язування задач на доведення не­рівностей.

Як варіант роботи на цьому етапі уроку (за умови відповідно­го рівня інтелектуальної активності учнів) моделюємо проблемну ситуацію (порівняти числа), розв'язання якої неможливе без ви­вчення властивостей числових нерівностей. У цьому разі завдан­ням уроку є розв'язання протиріччя між обсягом знань учнів, які в них є, та тими знаннями, які є необхідними для розв'язання поставленого завдання.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Порівняйте числа х і у, якщо різниця х – у дорівнює: 1) 8; 2) 0; 3) -1,5.
2. Доведіть нерівність:

1) х – 3 > х – 4;  2) х² + у² ≥ 2ху;  3) b + ≥ 2, b > 0; 4) , а ≥ 0.

3. Чи є правильним твердження:

1) якщо а = b, то b = а;   2) якщо а = b, b = с, то а = с;

3) якщо а = b, то а + с = b + с;  4) якщо а = b, то а – с = b – с;

5) якщо а = b, то ас = bс;   6) якщо а = b , то = ?

V. Формування знань

План вивчення нового матеріалу

1. Основні властивості числових нерівностей.
2. Наслідки з властивостей числових нерівностей.
3. Приклади застосування властивостей числових нерівностей та наслідків із них.

Опорний конспект № З

Методичний коментар

Одним із найважливіших базових умінь учнів, передбачених програмою з математики, є вміння здійснювати аргументовані мір­кування щодо оцінки значень виразів. Роботу з вироблення таких умінь було розпочато на попередніх двох уроках, проте на цих уро­ках для аргументації дій учнів були використані лише означення

порівняння чисел та в окремих випадках опорні нерівності. На даному уроці учні мають взяти на озброєння більш різноманітний перелік способів, представлених основними властивостями число­вих нерівностей. При формуванні знань учнів про ці властивості слід звернути увагу на такі моменти, які сприятимуть більш сві­домому засвоєнню учнями навчального матеріалу:

доведення властивостей числових нерівностей ґрунтується на означенні порівняння чисел (тобто ведеться через порівняння з нулем різниці лівої та правої частин деякої нерівності);

зміст властивостей бажано викласти як математичною мовою (у вигляді серії логічно пов'язаних між собою нерівностей), так і в словесній формі;

властивість 4 (див. опорний конспект № 3) виконується в да­ному вигляді тільки у випадку, коли числа додатні;

закріплення змісту кожної з доведених властивостей слід про­вести на певному конкретному прикладі.

Виходячи з вище сказаного, формування знань учнів бажано провести із якомога широким залученням учнів до роботи з до­ведення властивостей числових нерівностей.

VI. Формування вмінь

Усні вправи

1. Порівняйте числа:

1) m і n, якщо п > т;  2) т + 3 і п + 3, якщо т > п;

3) 3т і 3n, якщо т > п;  4) т і k, якщо т > п; n > k.

2. Відомо, що а > 5. Визначте (з обґрунтуванням), чи є правиль­ною нерівність:

1) а + 4 > 9;  2) 3а > 15;  3) –а < -5.

Письмові вправи

Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:

1. порівняти значення виразів, які містять змінні а і Ь, якщо відомо, наприклад, що, а < b;
2. використовуючи властивості числових нерівностей, записати правильні числові нерівності, що випливають з даної числової нерівності;
3. вправи, обернені до вправ, що розв'язувалися на уроці № 1;
4. довести числову нерівність, спираючись на властивості число­вих нерівностей.

Методичний коментар

Набір вправ, що дається для закріплення знань властивостей числових нерівностей і вироблення вмінь їх застосовувати для по­рівняння виразів, є традиційним. Традиційними залишаються ви­моги, яких мають дотримуватись учні під час розв'язування цих вправ. Такими обов'язковими вимогами є:

• чітке та повне відтворення відповідних властивостей число­вих нерівностей під час коментування учнями своїх дій при розв'язуванні запропонованих вправ;
• обов'язкове покрокове письмове обґрунтування дій при засто­суванні властивостей числових нерівностей.

VII. Підсумки уроку

Контрольне завдання

У наведених твердженнях знайдіть і виправте помилки, ура­ховуючи, що   т > n > 0, с > 0.

1) п < т;  2) т + с < п + с;  3) т + с < п;

4) ст. > сп;  5) ;   6) .

VIII. Домашнє завдання

1. Вивчити зміст та доведення властивостей числових нерівностей (див. опорний конспект № 3).
2. Розв'язати вправи на застосування властивостей числових не­рівностей, аналогічні вправам класної роботи.
3. На повторення: поняття подвійної нерівності та вправи на за­стосування цього поняття.