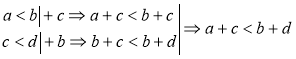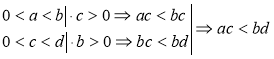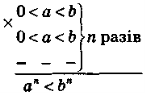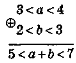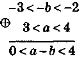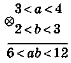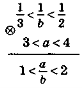Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання зна¬чення виразу.

Тема уроку. Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання зна­чення виразу.

Мета уроку: домогтися засвоєння учнями змісту поняття «додати не­рівності почленно» та «перемножити нерівності почленно», а також змісту властивостей числових нерівностей, що виражені теоремами про почленне додавання і почленне множення числових нерівностей і наслідків із них. Вироби­ти вміння відтворювати названі властивості числових нерівностей та використовувати ці властивості для оцінювання значення виразів, а також продовжити роботу з відпрацювання навичок доведення нерівностей, порівнян­ня виразів із використанням означення та властивостей числових нерівностей

Тип уроку: засвоєння знань, вироблення первинних умінь.

Наочність та обладнання: опорний конспект.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Учні виконують тестові завдання [9, тест 1] з наступною пере­віркою.

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів

Для свідомої участі учнів у формулюванні мети уроку можна запропонувати їм практичні завдання геометричного змісту (на­приклад, на оцінювання периметра та площі прямокутника, до­вжини суміжних сторін якого оцінено у вигляді подвійних нерівностей). Під час бесіди вчитель має спрямувати думку учнів на той факт, що хоча завдання є схожими на ті, що були розв'язані на по­передньому уроці (див. урок № 4, оцінити значення виразів), проте на відміну від названих не можуть бути розв'язані тими самими засобами, бо необхідно оцінити значення виразів, що містять дві (а в перспективі й більше) букви. Таким чином учні усвідомлюють існування протиріччя між знаннями, які вони отримали до цього моменту, та необхідністю розв'язання певної задачі.

Результатом виконаної роботи є формулювання мети уроку: ви­вчити питання про такі властивості нерівностей, які можуть бути застосовані у випадках, подібних до описаних у запропонованому учням завданні; для чого слід чітко сформулювати математич­ною мовою та у словесному вигляді, а потім довести відповідні властивості числових нерівностей та навчитися використовувати їх у комплексі з вивченими раніше властивостями числових не­рівностей для розв'язування типових задач.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Порівняйте числа а і b, якщо:

1) а – b = -0,2;   2) а – b = 0,002;    3) а = b – 3;  4) а – b = т²;  5) а = b – т².

2. Відомо, що 0 < а < 2. Оцініть значення виразу:
   1) a + 1; 2) а – 1; 3) 2а;  4)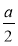 ;  5) .
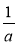3. Порівняйте значення виразів а + b і ab, якщо а = 3, b = 2. Від­повідь обґрунтуйте. Чи буде виконуватись одержане співвідно­шення, якщо:

1) а = -3, b = -2;  2) a = -3, b = 2?

V. Формування знань

План вивчення нового матеріалу

1. Властивість про почленне додавання числових нерівностей (з доведенням).
2. Властивість про почленне множення числових нерівностей (з доведенням).
3. Наслідок. Властивість про почленне множення числових не­рівностей (з доведенням).
4. Приклади застосування доведених властивостей.

Опорний конспект № 5

Методичний коментар

Для свідомого сприйняття нового матеріалу вчитель може на етапі актуалізації опорних знань та вмінь учнів запропонувати розв'язування усних вправ із відтворенням відповідно означення порівняння чисел та вивчених на попередніх уроках властивостей числових нерівностей (див. вище), а також розгляд питання про відповідні властивості числових нерівностей.

Зазвичай учні добре засвоюють зміст теорем про почленне до­давання та множення числових нерівностей, проте досвід роботи свідчить про схильність учнів до певних хибних узагальнень. Тому з метою попередження помилок при формуванні знань учнів з цьо­го питання шляхом демонстрацій прикладів та контрприкладів учителеві слід зробити наголос на таких моментах:

• свідоме застосування властивостей числових нерівностей неможливе без уміння записувати ці властивості як математич­ною мовою, так і в словесному вигляді;
• теореми про почленне додавання та множення числових не­рівностей виконуються тільки для нерівностей однакових знаків;
• властивість про почленне додавання числових нерівностей ви­конується за певної умови (див. вище) для будь-яких чисел, а теорема про почленне множення (у тому вигляді, як це за­явлено в опорному конспекті № 5) тільки для додатних чисел;
• • теореми про почленне віднімання та почленне ділення число­вих нерівностей не вивчаються,, тому у випадках, коли необ­хідно оцінити різницю або частку виразів, ці вирази подаються у вигляді суми або добутку відповідно, і далі вже за певних умов використовують властивості про почленне додавання та множення числових нерівностей.

VI. Формування вмінь

Усні вправи

1. Додайте почленно нерівності:

1) а > 2, b > 3;   2) с < -2, d < 4.

Чи можна ті самі нерівності почленно перемножити? Відповідь обґрунтуйте.

2. Перемножте почленно нерівності:

1) а > 2, b > 0,3;   2) с > 2, d > 4.

Чи можна ті самі нерівності додати? Відповідь обґрунтуйте.

3. Визначте й обґрунтуйте, чи є правильним твердження, що якщо 2 < а < 3, 1 < b < 2, то:

1) 3 < а + b < 5;   2) 2 < аb < 6;   

3) 2 – 1 < а – b < 3 – 2;    4) ?

Письмові вправи

Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:

1. додати та перемножити почленно дані числові нерівності;
2. оцінити значення суми, різниці, добутку та частки двох виразів за даними оцінками кожного з цих чисел;
3. оцінити значення виразів, що містять дані букви, за даними оцінками кожної з цих букв;
4. довести нерівність із використанням теорем про почленне до­давання та множення числових нерівностей і з використанням класичних нерівностей;
5. на повторення властивостей числових нерівностей, вивчених на попередніх уроках.

Методичний коментар

Письмові вправи, що пропонуються для розв'язання на цьо­му етапі уроку, мають сприяти виробленню сталих навичок по-членного додавання і множення нерівностей у простих випадках. (При цьому відпрацьовується дуже важливий момент: перевірка відповідності запису нерівностей до умови теорем та правильний запис суми і добутку лівої та правої частин нерівностей. Підготовча

робота проводиться під час виконання усних вправ.) Для кращого засвоєння матеріалу слід вимагати від учнів відтворення вивчених теорем при коментуванні дій.

Після успішного опрацювання учнями теорем у простих ви­падках вони можуть поступово переходити до більш складних випадків (на оцінювання різниці та частки двох виразів і більш складних виразів). На цьому етапі роботи вчителеві слід уважно слідкувати за тим, щоб учні не припустилися типових помилок, намагаючись різницю та частку оцінювати за власними хибними правилами.

Також на уроці (звісно, якщо дозволяє час та рівень засво­єння учнями змісту матеріалу) слід приділити увагу вправам на застосування вивчених теорем для доведення більш складних не­рівностей.

VII. Підсумки уроку
Контрольне завдання

Відомо, що 4 < а < 5; 6 < b < 8. Знайдіть неправильні нерівності і виправте помилки. Відповідь обґрунтуйте,

1) 10 < а + b < 13;  2) -4 < а – b < -1;   3) 24 < аb < 13;

4) ;   5) ;  6) 16 < а² < 25;

7) 100 < а² + b² < 169?

VIII. Домашнє завдання

1. Вивчити теореми про почленне додавання і множення числових нерівностей (з доведенням).
2. Виконати вправи репродуктивного характеру, аналогічні впра­вам класної роботи.
3. На повторення: вправи на застосування означення порівняння чисел (на доведення нерівностей та на порівняння виразів).