Основні задачі на розв'язування трикутників.

 

Тема уроку. Основні задачі на розв'язування трикутників.

Мета уроку: ознайомити учнів з основними задачами розв'язування трикутників.

Тип уроку: комбінований.

Наочність і обладнання: таблиця «Співвідношення між сторонами і кутами трикутника» [13].

Вимоги до рівня підготовки учнів: описують основні випадки розв'язування трикутників та алгоритми їх розв'язування.

Хід уроку

І. Перевірка домашнього завдання

Фронтальне опитування

1. Сформулюйте теорему косинусів.
2. Як, користуючись теоремою косинусів, можна знайти кути, якщо відомі довжини сторін трикутника?
3. Як, знаючи лише довжини сторін трикутника, визначити вид трикутника (за кутами)?
4. Сформулюйте теорему синусів.
5. Як можна знайти радіус кола, описаного навколо трикутника, якщо відомі сторона трикутника і протилежний до неї кут?
6. Сформулюйте теорему про співвідношення між кутами три­кутника і протилежними сторонами.
7. Сформулюйте теорему про співвідношення між сторонами трикутника і протилежними кутами.

Правильність виконання задачі з домашнього завдання пере­вірити за записами на дошці, зробленими до початку уроку.

Розв'язання

a² = b² + c² – 2bccosA; 49 = 4 + 64 – 2 ∙ 2 ∙ 8 ∙ cosA; 49 = 68 – 32cosA;

32cosA = 19; cosA = 0,594; A 54°.

b² = a² + c² – 2accosB; 4 = 49 + 64 – 2 ∙ 7 ∙ 8 ∙ cosB; 4 = 113 – 112cosB;

112cosB = 109; cosB = 0,973; B 13°.

C = 180° - A - B 180° - 54° - 13° = 113°.

Відповідь. A 54°, B 13°, C 113°.

 

ІІ. Аналіз самостійної роботи

 

ІІІ. Поетапне сприймання й усвідомлення нового матеріалу

Визначення трикутника за трьома основними елементами

З ознак рівності трикутників випливає, що трикутник визна­чається трьома основними елементами, серед яких хоча б один лінійний. Розв'язати трикутник означає за його трьома даними основними елементами знайти три інші елементи.

Із шести основних елементів трикутника по три елементи можуть сполучатися такі:

1. сторона і два прилеглі кути;
2. дві сторони і кут між ними;
3. дві сторони і кут, протилежний одній із сторін;
4. три сторони.

 

Чотири випадки розв'язування трикутників

Відповідно до цього розглянемо чотири випадки розв'язування трикутників.

1-й випадок

Нехай задано сторону а і кути А і В трикутника ABC. Треба знайти кут С і сторони b і с трикутника ABC.

С = 180° - (A + В).

За теоремою синусів , знайдемо .

За теоремою синусів , знайдемо

= = .

 

Колективне розв'язування задач

Дано сторону а = 5 і два кути трикутника β = 30°, γ = 45°. Знайдіть третій кут та інші дві сторони трикутника.

Розв'язання

α = 180° - β - γ = 180° - 30° - 45° = 105°.

; ; ; b 2,59.

; ; ; с 3,66.

Відповідь, α = 105°, b 2,59, с 3,66.

 

Самостійне розв'язування задач

Дано сторону і два кути трикутника. Знайдіть третій кут та інші дві сторони трикутника, якщо:

варіант 1: а = 20, α = 75°, β = 60°;

варіант 2: а = 35, β = 40°, γ = 120°.

Варіант 1

Розв'язання

γ = 180° - α - β = 180° - 75° - 60° = 45°.

; ; ; b 17,9.

; ; ; с 14,6.

Відповідь. γ = 45°, b 17,9, с 14,6.

Варіант 2

Розв'язання

α = 180° - β - γ = 180° - 40° - 120° = 20°.

; ; ; b 65,8.

; ; ; c 88,6.

Відповідь, α = 20°, b 65,8, c 88,6.

 

2-й випадок

Нехай задано сторони а і b та кут між ними С. Треба знайти сторону с та кути В і А. Сторону с знайдемо за теоремою косинусів: с² = a² + b² – 2abcosC,    c = .

Кут А можна знайти за теоремою косинусів:

a² = b² + c² – 2bccosA, звідси .

Кут А можна знайти за теоремою синусів:

, звідси .  

Тоді B = 180° - A - C.

 

Колективне розв'язування задач

Дано дві сторони трикутника b = 14, с = 10 і кут між ними α = 145°. Знайдіть інші два кути і третю сторону трикутника.

Розв'язання

a² = b² + c² – 2bccosα; a² = 196 + 100 – 2 ∙ 14 ∙ 10 ∙ cos145° 296 + 280 ∙ 0,8192 296 + 229,36 = 525,36; а 22,9.

; ; sinβ 0,3507; β 21°.

γ = 180° - α - β 180° - 145° - 21° = 14°.

Відповідь, а 22,9, β 21°, γ 14°.

 

Самостійне розв'язування задач

Дано дві сторони трикутника і кут між ними. Знайдіть інші два кути та третю сторону трикутника, якщо:

варіант 1: а = 7, b = 23, γ = 130°;

варіант 2: b = 9, с = 17, α = 95°.

Варіант 1

Розв'язання

с² = а² + b² – 2abcosγ = 7² + 23² – 2 ∙ 7 ∙ 23 ∙ cos130°49 + 529 – 322 ∙ (-0,64) = = 578 + 206,08 = 784,08; с 28.

a² = b² + c² – 2bccosα; 7² = 23² + 28² – 2 ∙ 23 ∙ 28 ∙ cosα;

49 = 529 + 784 – 1288cosα; 1288cosα = 1264; cosα 0,98; α 11°.

Тоді β = 180° - α - γ 180° - 130° - 11° = 39°.

Відповідь. с 28, α 11°, β 39°.

Варіант 2

Розв'язання

a² = b² + c² – 2bccosα = 9² + 17² – 2 ∙ 9 ∙ 17 ∙ cos95° 81 + 289 – 306 ∙ (-0,09) = = 370 + 27,54 = 397,54; a 19,9.

b² = a² + c² – 2accosβ; 9² = 397,54 + 17² – 2 ∙ 19,9 ∙ 17 ∙ cosβ;

81 = 686,54 – 676,6cosβ; 676,6cosβ = 605,54; cosβ 0,895; β 26°.

Тоді γ = 180° - α - β = 180° - 26° - 95° = 59°.

Відповідь, а 19,9, β 26°, γ 59°.

 

3-й випадок

 Нехай задано три сторони а, b, с трикутника ABC. Треба знайти кути А, В, С. За теоремою косинусів знайдемо кут А:

а² = b² + с² – 2bccosA , звідси .

Тоді за теоремою синусів знайдемо кут В: , звідси . І, нарешті, С = 180° - (A + В).

 

Колективне розв'язування задач

Дано три сторони трикутника a = 1, b = 3, с = 4. Знайдіть його кути.

Розв'язання

а² = b² + с² – 2bccosα; 4 = 9 + 16 – 24cosα; 24cosα = 21; cosα = = 0,875;

α 29°.

; ; sinβ 0,7272; β 47°.

γ = 180° - α - β 180° - 29° - 47^o = 104°.

Відповідь, α 29°, β 47°, γ 104°.

 

Самостійне розв'язування задач

Дано три сторони трикутника. Знайдіть його кути, якщо:

варіант 1: a = 15, b = 24, с = 18;

варіант 2: a = 23, b = 17, с = 39.

Варіант 1

Розв’язання

a² = b² + c² – 2bccosα; 225 = 576 + 324 – 864cosα; cosα = 0,7813;

α 38,62 39°.

; ; ; ;

β 87°.

γ = 180° - α - β 180° - 39° - 87° = 54°.

Відповідь. α 39°, β 87°, γ 54°.

Варіант 2

Розв'язання

a² = b² + c² – 2bccosα; 529 = 289 + 1521 – 1326cosα; 0,9661;  α 15°.

; ; ; sinβ 0,1913; β 11°.

γ = 180° – α – β 180° – 15° - 11° = 154°.

Відповідь, α 15°, β 11°, γ 154°.

 

4-й випадок

Нехай задано дві сторони а і b та кут А трикутника ABC. Треба знайти кути В і С та сторону с.

За теоремою синусів маємо .

Якщо bsinA > a, то задача не має розв'язків (оскільки sinβ > 1, що неможливо).

Якщо bsinA = a, то B = 90°, тоді C = 90° - A, c = bcosA.

Якщо bsinA < a, тоді існують два кути, синуси яких до­рівнюють : один із цих кутів гострий, а другий — тупий.

Якщо a > b, то A > B. A, оскільки, у трикутника не може бути два тупих кути, то кут В гострий і розв'язок єдиний.

Якщо а < b, то існують два кути В₁ і В₂ (B₂ = 180° - B₁), синуси яких дорівнюють . У цьому випадку задача має два розв'язки:

C₁ = 180° - A - B₁, ;

C₂ = 180° - A - B₂, .

 

Колективне розв'язування задач

1. У трикутнику дано дві сторони а = 2, b = 4 і кут α, який протилежний до однієї із сторін, становить 60°. Знайдіть інші два кути і третю сторону трикутника.

Розв'язання

; ; sinβ = = 2sin60° = 2 ∙ = > 1.

Задача розв'язків не має.

Відповідь. Розв'язків немає.

 

2. Дано дві сторони трикутника: а = 6, b = 8 і кут α, який про­тилежний до однієї із сторін, становить 30°. Знайдіть інші два кути і третю сторону трикутника.

Розв'язання

; ; sinβ = 0,6667;

β 42° або β 180° - 42° = 138°.

Якщо β 42°, тоді γ = 180° - α - β 180° - 30° - 42° = 108° і ; ; .

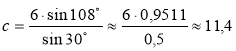Якщо β = 138°, тоді γ = 180° - α - β 180° - 30° - 138° = 12° і ; ; .

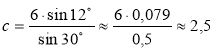Відповідь. β 42°, γ 108°, с 11,4 або β 138°, γ 12°, с 2,5.

 

IV. Домашнє завдання

Розв'язати трикутники:

а) с = 14, α = 64°, β = 48°;

б) а = 24, с = 18, β = 15°;

в) а = 55, b = 21, с = 38;

г) а = 32, с = 23, β = 152°.

 

V. Підбиття підсумків уроку

Запитання до класу

1. Що означає розв'язати трикутник?
2. Які є основні типи задач на розв'язування трикутників?