Презентація "Геометричні перетворення"
Про матеріал
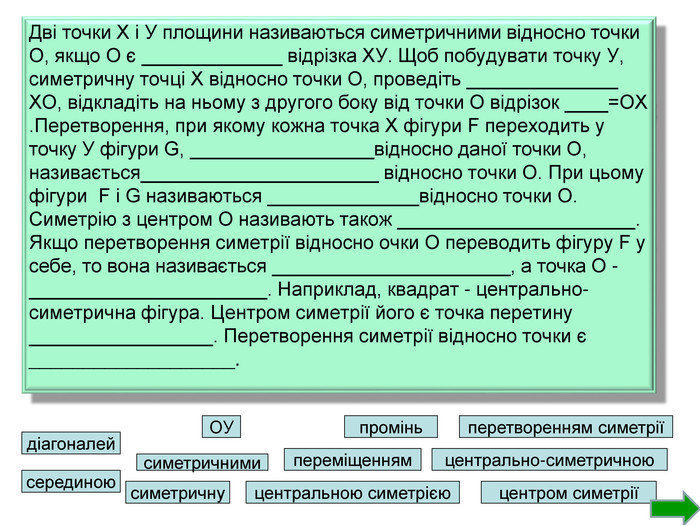
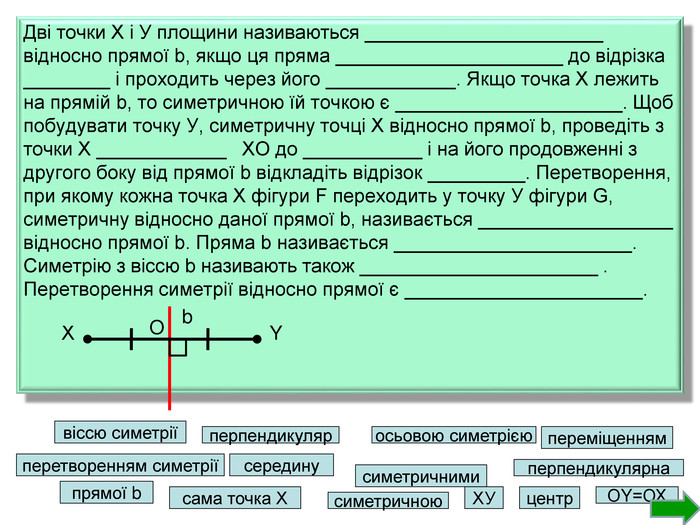
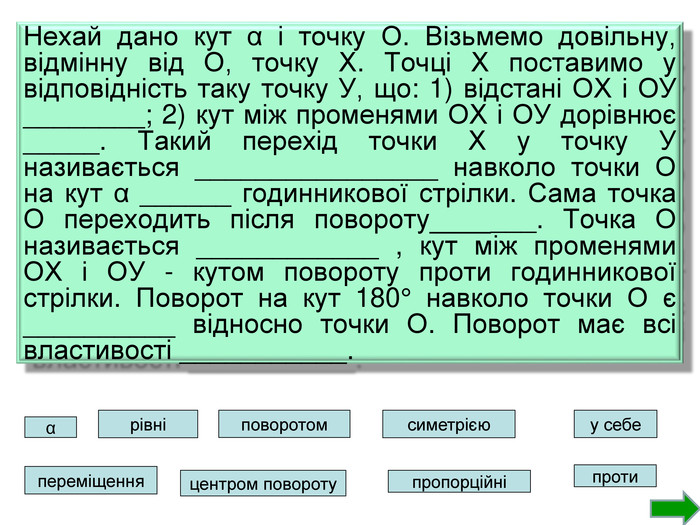
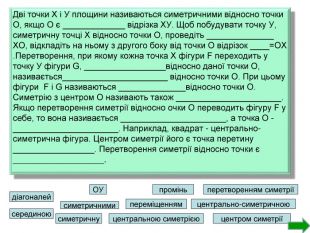
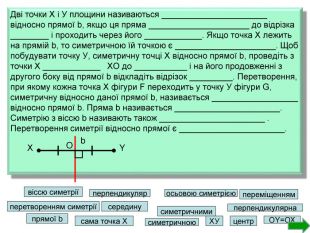
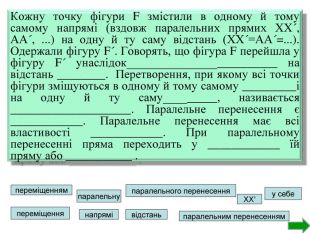
Розділ геометрії «Геометричні перетворення» представлений у вигляді презентації, призначений для використання на уроках геометрії у 9 класі. Дана презентація містить тестові завдання, які допоможуть перевірити знання учнів з даної теми. Сподіваюся, що цей матеріал принесе користь учителю математики та учням. Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія 9 клас (Бурда М.І., Тарасенкова Н.А.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку