Означення степеня з цілим показником
Тема уроку: Означення степеня з цілим показником.
Мета: домогтися засвоєння учнями змісту означення степеня з цілим від’ємним показником (для цілої та дробової основи степеня); сформувати вміння відтворювати означення степеня та застосовувати його для перетворення степеня з цілим від’ємним показником у дріб, та навпаки; сформувати вміння розв’язувати вправи на застосування вивченого означення; розвивати обчислювальні навички; сприяти вихованню інтересу до математики, активності, організованості, уміння взаємоконтролю і самоконтролю своєї діяльності, формувати позитивний мотив навчання, розвиток умінь навчально-пізнавальної діяльності.
Тип уроку: засвоєння знань та первинних умінь.
Хід уроку
І. Організаційний момент
ІІ. Вступна бесіда
Діти сьогодні на уроці ми з вами починаємо вивчати тему «Степінь з цілим показником». З поняттям «степінь з натуральним показником» ви вже знайомі. Поняття степеня відіграє велику роль не тільки в математиці, а й у фізиці, хімії, астрономії, географії, медицині. За допомогою степеня записують дуже великі або дуже маленькі числа.. Наприклад: маса атома водню дорівнює 1,66∙10 -27 кг, маса електрона 9∙10 -31 кг, маса Землі 6∙10 21 т.
Ще за часів Вавилону, майже 4 тис. років тому, вчені працювали з числами, які містили однакові множники. Такі числа отримували при обчисленні площі або об’єму. Але записували їх в такому вигляді:5aaaaabbbbb, 3ppppkkkcc. Діти допоможіть мені записати ці числа у вигляді степенів.
ІII. Актуалізація опорних знань та вмінь учнів
Один учень з класу записує біля дошки властивості степенів з натуральним показником, а інші в цей час працюють над вправами.
Усне опитування
- Прочитайте вираз, назвавши основу і показник степеня:
1) 54; 2) 6,19; 3) 101;
4) (-8)5; 5) 017; 6) ![]() .
.
- Визначте знак виразу, не виконуючи піднесення до степеня:
1)![]() ; 2)
; 2)![]() ; 3)
; 3) ![]() ;
;
4) (-4)9 5) -210 6) (-7)10;
- Обчисліть:
![]()
![]() ;
; ![]() .
.
Мотивація навчальної діяльності.
Чому дорівнює ![]() ?
?
Отже, знань про степінь недостатньою. Розв’язування цієї проблеми є метою нашої навчальної діяльності на уроці.
ІV. Повідомлення теми і мети уроку
Сьогодні на уроці ми з вами вивчимо означення степеня з цілим показником, навчимося застосовувати набуті знання на практиці (Відкрийте зошити, запишіть сьогоднішнє число, тема…)
V. Вивчення нового матеріалу
Степінь з цілим показником включає три види степеня:
1) степінь з цілим додатним показником (ототожнюється зі степенем з натуральним показником, вивченим у 7 кл.)
2) степінь з нульовим показником (випливає з властивості):
![]()
![]() де (
де (![]() )
)
![]() - не має змісту
- не має змісту
Приклади: 110=1; (-0,7)0=1; (![]() )0=1.
)0=1.
3) степінь з цілим від’ємним показником:
Розглянемо ряд чисел, кожне число якого менше від попереднього в 10 разів:
1000, 100, 10, 1, ![]() ,
, ![]() ,
, ![]() , …
, …
Скористаємось властивостями степеня і запишемо цей ряд у вигляді:
103, 102, 101, 100, ![]() ,
, ![]() ,
, ![]() ,….
,….
Показник степеня починаючи з другого на 1 менший від показника попереднього степеня. Якщо поширити цю закономірність на числа, що стоять праворуч від 101 отримаємо:
103, 102, 101, 100, 10-1, 10-2, 10-3.
Отже, 100 =1, 10-1 = ![]() , 10-2 =
, 10-2 = ![]() , 10-3 =
, 10-3 = ![]() .
.
Виходить, що: ![]() , якщо а
, якщо а![]()
Ось таким чином ми з вами вивели означення степеня з цілим від’ємним показником.
Якщо n- ціле від’ємне число і а![]() то
то ![]()
Якщо![]() n- натуральне число і a
n- натуральне число і a![]() , то
, то ![]()
Приклади
-
 (приклад з мотивації)
(приклад з мотивації)
-

-
 =
=
Означення степеня з цілим показником для основи ![]() :
:
якщо ![]() , n- натуральне число, то
, n- натуральне число, то ![]() = (
= (![]()
Приклади
До записаних на дошці властивостей під час актуалізації дописуємо ще 3 властивості:
![]() де (
де (![]() )
)
![]() , якщо а
, якщо а![]() , n — натуральне число
, n — натуральне число
![]() = (
= (![]()
![]() , , n — натуральне число
, , n — натуральне число
VІ. Формування умінь і навичок.
Робота з підручником
1.Усне виконання вправ: №454, 455, ст.99
2.Письмово: №458, №459(напівсамостійно під контролем учителя) ст.100
Фізкультхвилинка
3.Робота з картками ( учні розв’язуючи приклади відкривають зашифровану букву під правильною відповіддю до прикладу і складають слово)
Картка

Обчислити:
-
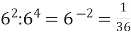 «М»
«М»
-
 «О»
«О»
-
 =
= 0 «Л»
0 «Л»
-
 «О»
«О»
-
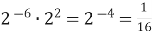 «Д»
«Д»
-
 «Ц»
«Ц»
-
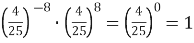 «І»
«І»
Перевірочне слово: молодці
4.Самостійна робота
Тестові завдання (на картках)
Варіант 1
1. Тотожно рівним виразу 7-3 є вираз:
а) -73; б)![]() в)
в) ![]() г)
г) ![]() .
.
2. Тотожно рівним дробу ![]() є вираз:
є вираз:
а) 23 ; б) 24; в) 4-2; г) 2-3
3. Значення виразу 2-3 + 2-2 дорівнює:
а) -10; б) ![]() ; в)
; в) ![]() ; г) 12.
; г) 12.
4. Тотожним до степеня ![]() -2 є вираз:
-2 є вираз:
а) ![]() -2 ; б)
-2 ; б)![]() в)
в)![]() 2 г)
2 г) ![]() ∙(-2)
∙(-2)
Варіант 2
1. Тотожно рівним виразу 5-2 є вираз:
а) -52; б)![]() в)
в) ![]() г)
г) ![]() .
.
2. Тотожно рівним дробу ![]() є вираз:
є вираз:
а) 32 ; б) 33; в) 3-3; г) 3-2
3. Значення виразу 2-3 + 2-1 дорівнює:
а) -10; б) ![]() ; в)
; в) ![]() ; г) 12.
; г) 12.
4. Тотожним до степеня ![]() -2 є вираз:
-2 є вираз:
а) ![]() 2 ; б)
2 ; б)![]() в)
в)![]() -2 г)
-2 г) ![]() ∙(-2)
∙(-2)
Відповіді: В1 б), г), б), в)
В2 б), в), в), а).
VІI. Підсумок уроку
Про що дізналися на уроці?
Виставлення та мотивація оцінок
VIII. Домашнє завдання
Параграф 10, №461, №465, №466
1


про публікацію авторської розробки
Додати розробку
