Паралельні прямі. Ознаки паралельних прямих . Презентація
Про матеріал
Тема уроку: "Паралельні прямі. Ознаки паралельних прямих"
Мета уроку:
Ознайомити учнів з поняттям паралельних прямих.
Навчити визначати ознаки паралельності прямих.
Формувати навички застосування теоретичних знань на практиці.
Розвивати логічне мислення та просторову уяву. 
Перегляд файлу
Повторимо.
Паралельні прямі
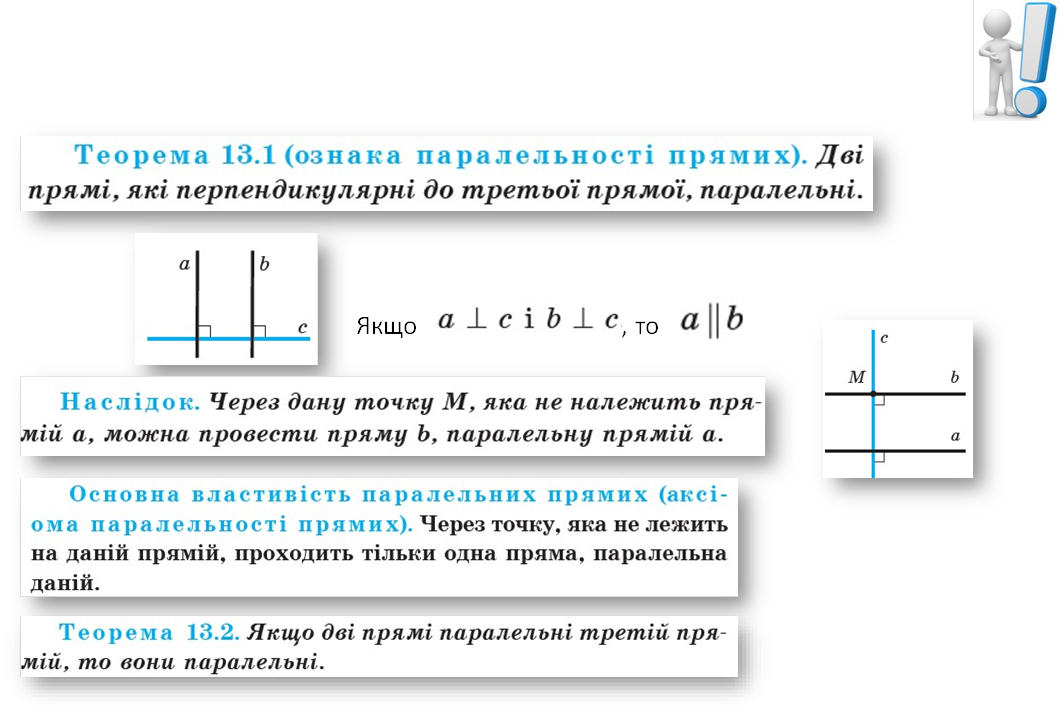Повторимо.
Паралельні прямі
 |
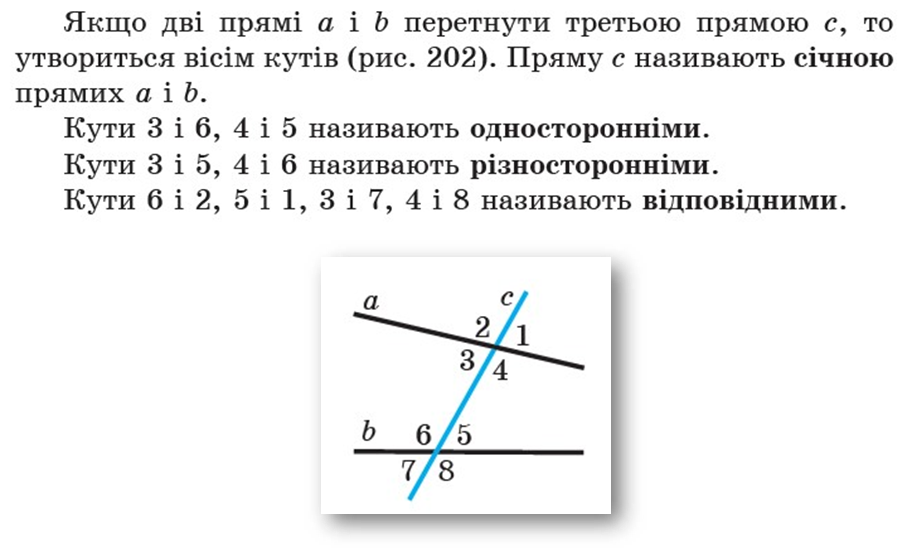Види кутів, що утворюються при перетині двох прямих третьою прямою
 |
Так як АВ=BС, то ∆АВС – рівнобедрений з основою АС. Тоді ∠ВАС=∠ВСА.
Так як CD=DK, то ∆СDK– рівнобедрений з основою СK. Тоді ∠DKС=∠DСK.
∠ВСА=∠DСK, вертикальні кути. Тоді ∠ВАС=∠DKС.
∠ВАС і ∠DKС різносторонні при прямих АВ і DK та січній АК.
Отже, за ознакою паралельності прямих АВ∥DK.
Так як АК – бісектриса ∠ВАС, то ∠МАК=∠САК.
Так як АМ=МК, то ∆АМК – рівнобедрений з основою АК. Тоді ∠МАК=∠МКА.
Отже, ∠САК=∠МКА.
∠САК і ∠МKА різносторонні при прямих МК і АС та січній АК.
Отже, за ознакою паралельності прямих МК∥АС.
Домашнє завдання
Підручник ГЕОМЕТРІЯ 7, А. Г. Мерзляк
П. 14, №№ 306, 308
Виконати тестування за посиланням
https://naurok.com.ua/test/join?gamecode=8075020(спроб 1 , активний до 18.01.2022
pdf
Оцінка розробки
Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку