Перелік задач для теми "Лінійні програми"

Задачі для самостійного розв’язання:

A) Задачі на обчислення функцій, виразів:

1. Для двох дійсних чисел визначити  їх суму, добуток, різницю та частку.

2. Дано два дійсних числа Х і У. Одержати

3. Дано два дійсних додатних числа. Знайти середнє арифметичне і середнє геометричне цих чисел.

4. Дано x, y. Обчислити а і b, якщо

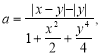
5. Дано x, y, z. Обчислити а і b, якщо

6 . Дано x, y. Обчислити а і b, якщо

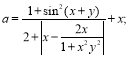
7.   Задане дійсне число x. Надрукувати за зростанням такі числа tgx, 1+|x| та (1+x²)⁴.
8. Задане значення дійсної величини x. Визначити .
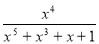9. Дано дійсні числа с, d. Обчислити

де х1,х2 - корені рівняння х² -3х-|сd|=0.

 10. Дано x. Обчислити 2x⁴ - 3x³ + 4x³ - 5x + 6. Подбати про економію операцій.

 11. Дано x. Вычислить 1 - 2x +3x² - 4x³  и  1 + 2x +3x² + 4x³. Подбати про економію операцій.

B) Математичні,  фізичні задачі:

1. Дана довжина ребра куба. Знайти об’єм куба і площу його бокової  поверхні.
2. Дано катети прямокутного  трикутника. Знайти його гіпотенузу і площу.
3. Змішано V1 літрів води з температурою t1  і  V2  літрами  води з температурою t2. Знайти об’єм і температуру  сумішу.
4. Задана сторона рівностороннього трикутника. Знайти площу цього трикутника.
5. Знайти площу кільця з радіусами R і r.
6. Обчислити відстань між  двома  точками  з  координатами   х1,у1 і х2,у2.
7. Обчислити  довжину окружності і площу кола заданого  радіусу.
8. Обчислити периметр і площу прямокутного  трикутника по довжинам його катетів.
9. По  координатам  трьох вершин деякого  трикутника знайти його площу і периметр.
10.  Велосипедист Микола, стартувавши у точці (х₀, y₀) та рухаючись по прямій А(х-х₀)+В(y-y₀+C=0, мріє про те, як він покатає на своєму велосипеді сусідку Катрусю. Чи здійсняться мрії Миколи, якщо недалеко, у точці (p, q), росте дерево?
11.  Від морського вокзалу відійшли одночасно у протилежних напрямках теплохід та турист. Теплохід рухався зі швидкістю V₁ км/год, а турист по стежці вздовж річки зі швидкістю V₂ км/год. Якщо через N годин турист передумає і вирішить поплисти річкою назад за теплоходом зі швидкістю V₃ км/год, то чи встигне він підсісти на теплохід, який має за графіком зупинку через Y годин після початку руху і стоїть на цій зупинці Z годин? Зважати на те, що всі події відбувалися протягом однієї доби.
12.  Щоб бути завжди чистою, людині необхідно х (24  х  50) шматків мила на рік. Якщо мити лише п’яти, то мила знадобиться у 12 разів менше, а тільки вуха – ще на один шматок менше. Скласти програму, яка б за вибором користувача давала відповідь, яку кількість шматків мила необхідно закупити на n років вперед, щоб:

• митися повність;
• мити лише вуха;
• мити лише п’яти;
• мити п’яти і вуха;

С)  Задачі про числа:

1.  Знайти  добуток  цифр  заданого  чотиризначного числа.

2. Визначити число, яке отримане виписуванням в зворотному порядку цифр даного тризначного числа.

3. Чи впізнає себе дільник m у залишку після ділення на нього націло числа n?
4. Одно число в 2 рази більше другого, а їх сума дорівнює 93.  Знайти ці числа. 
5. Написати програму, яка  для  заданого цілого числа а надрукує наступну таблицю:

                    а

                    а³    а⁶

                    а⁶    а³    а

6. Дано дві звичайні дроби. Скласти програму, яка знайде суму, різницю, добуток та частку цих двох дробів.
7. Складіть програму для обчислення суми цифр введеного з клавіатури чотиризначного натурального числа.
8. Дано натуральне трьохзначне число. Получити нове число, для цього приписати до даного таке  ж саме число.
9. Дано натуральне п’ятизначне число. Знайти першу та останню його цифру.
10.  Дано натуральне п’ятизначне число. Знайти другу з початку його цифру.
11.  Дано натуральне п’ятизначне число. Знайти перші дві його цифри.

D) Задачі з казковими,  літературними  персонажами:

1. Чебурашка вирішив купити килими, щоб застелити кімнату, в якій він мешкав разом з Геною. Розмірами їхньої прямокутної кімнати виявилися цілі числа a і b. Коли Чебурашка запитав у магазині, які розміри квадратних килимів, що були у продажі, то продавець назвав ціле число с. Яку кількість килимів необхідно закупити Чебурашці, щоб накрити максимальну площу кімнати? Килими не можна накладати та підгортати. Визначити, яка площа кімнати буде не накритою килимами. Передбачити ситуацію, коли розміри килима перевищують розміри кімнати.
2. На квадратному городі, довжина всіх сторін якого дорівнює 80м, посадили собаку. Цього собаку посадили на ланцюг довжиною n м та m см і прикріпили ланцюг до стовпа, який стирчить в самому центрі города. Довжина собаки від ошийника до передніх зубів – 30см. Чи залишилось на городі місце, безпечне для злодіїв?
3. Толя посперечався з Миколою, хто з’їсть більше баночок гуталіну. Микола з’їв х, а Толік – y. Визначити, хто виграв. Скільки баночок гуталіну забезпечило перемогу тому, хто виграв?
4. Вовочка твердо вирішив стукнути старшокласника Єгора по лобі дошкою площею S кв.м. Визначити, чи підійде для цієї справи дошка прямокутної форми шириною а см та довжиною b см.
5. Васєчкін прочекав у черзі на щеплення x хвилин. Визначити, скільки годин і хвилин він чекав. Порівняти, чого виявилося більше – годин чи хвилин.
6. Іван Петрович надягнув нові штани і сів на тільки що пофарбовану табуретку. На його штанах з’явилася квадратна пляма зеленого кольору, довжина якої становила а см. Виявилося, що у хімчистку беруть одяг, плями на якому завбільшки до S см². Визначіть, чи вдалося Іванові Петровичу врятувати свої штани?
7. Том Сойєр фарбує паркан своєї тітоньки. Нехай а – довжина, а b – ширина суцільного зафарбованого прямокутника в метрах, S – сумарна площа плям фарби на решті паркана в квадратних метрах. Тітонька вирішила, що якщо площа прямокутника буде більша за 15 кв.м., а площа плям не більша за 10 кв.м., то Том отримає яблуко, інакше – догану по службі. Визначіть, що чекає Тома?
8. Змій Горинич застудився. Для його одужання потрібно не менше 10 та не більше 15 кг вітаміну С або більше 20 літрів гарячого чаю. Змій з’їв х яблук (по 0,05 г вітаміну С в кожному) та випив y склянок чаю (по 200 г кожна). Визначити, чи одужає Змій Горинич. Якщо ж ні, то скільки літрів чаю або скільки яблук йому не вистачило для цього?
9. На одному маленькому квадратному безлюдному острові зі стороною а м мешкали k потерпілих корабельну аварію Робінзонів. Чи не порушені їхні права на житло, якщо на кожного Робінзона повинно припадати S м²? Скільком Робінзонам ще вистачить місця на острові, якщо поблизу трапиться нова аварія?
10. Жили-були дідусь і бабуся і був у них город прямокутної форми. Довжина городу була А м, а ширина складала В м. Якось дідусь посварився з бабусею і вирішив поділити город порівну. Тепер у дідуся є квадратний город зі стороною С м, відрізаний скраю, а решта дісталася бабусі. Визначіть, чи не залишилась бабуся ошуканою та якої форми дістався їй город: прямокутної чи квадратної?
11. Трьом Товстунам подали на десерт кремові тістечка. Вага одного тістечка складала х кг, а вага Товстунів відповідно х₁, х₂ та х₃ кг. Перший Товстун з’їв n тістечок, другий – у два рази більше від другого, але кожний з них не міг з’їсти більше, ніж половина його власної ваги. Скільки тістечок було з’їдено Товстунами за обідом?
12. Три міліціонери гналися по прямій стежці за одним злочинцем. Вусатий  міліціонер біг зі швидкістю х км/год, лисий міліціонер – на 5 км/год швидше, а пузатий міліціонер – ще на 5 км/год швидше за лисого. Злочинець тікав зі швидкістю y км/год. Пробігши n годин, злочинець заліз на березу і причаївся. А міліціонери, пробігши по m годин кожний без сніданку, обіду та вечері, зупинились і всі троє підняли голови вгору. Той, в полі зору якого (до 5 метрів) виявився злочинець, був дуже щасливим і заарештував його. Визначити, хто з міліціонерів виявився щасливим, а хто залишився сумним? Скільки годин до арешту просидів на березі злочинець? Яка відстань була між міліціонерами в момент арешту злочинця?

Е) Задачі із змінними логічного типу:

1. Написати програму, яка друкує true або false в залежності від того, чи мають три  даних цілих числа однакову парність чи ні.
2. Написати програму, яка друкує true або false в залежності від того, чи більше значення числа е у степені PI значення числа PI у степені е чи ні .   (Числа  е  і  PI з точністю 10-5 описати як константи).
3. Для довільних дійсних чисел a,b і c визначити, чи має повне квадратне рівняння хоча б один дійсний розв’язок.
4. Для довільних дійсних чисел a,b і c визначити, чи має повне квадратне рівняння два  дійсних розв’язка.
5. Визначити, чи дорівнює сума двох перших цифр даного чотиризначного числа сумі двох його останніх цифр.
6. Визначити, чи дорівнює квадрат даного тризначного числа кубу суми цифр цього числа.
7. Дано три довільних числа. Визначити, чи можна побудувати  трикутник з такими довжинами  сторін.
8. Дано три сторони трикутника. Визначити, чи прямокутний цей  трикутник.
9. Дано три сторони трикутника. Визначити, чи є цей трикутник рівнобедрений.
10. Дано три сторони трикутника. Визначити, чи є цей трикутник рівносторонній.
11. Визначити, чи є  дане двозначне число паліндромом.
12. Визначити, чи є дане тризначне число паліндромом.
13. Визначити, чи є дане чотиризначне число паліндромом.
14. Визначити, чи можна вписати коло з радіусом R, у квадрат зі стороною А.
15. Визначити, чи можна вписати квадрат зі стороною  А у коло радіусом R.
16. Визначити, чи є число А найбільшим з чисел А, В, С.
17. Дано квадрат зі стороною А і коло радіусом R. Визначити чи рівновеликі ці фігури.