Підготовка до ЗНО з теми "Арифметична прогресія"

Підготовка до ЗНО

Арифметична прогресія

 «Послідовність, у якій кожен наступний член, починаючі з другого, є сумою попереднього, та деякого одного і того самого числа називається арифметичною прогресією».

 Одне й те саме число, яке ми додаємо до попереднього числа, щоб отримати наступне, називається різницею прогресії d.

Кожний наступний а₂ = а₁ + d; а₃ = а₂ + d; а₄ = а₄ + d.

 d = а₂ – а₁

 d = а_n – а_{n – 1} (номер на 1 менше.)

а_n = а_{n – 1} + d

           Розглянемо послідовність:

3;5;7;9 … а₁ = 3, а₂ = 7, d = а₂ – а₁ = 7 – 3 = 2 – зростаюча послідовність.

8;3; – 2; – 9 … а₁ = 3, а₂ = 7, d = а₂ – а₁ = 3 – 8, d = – 2 – спадаюча послідовність.

            Обидві прогресії нескінчені. Позначення арифметичної прогресії а_n.

 Формула загального члена арифметичної прогресії: а₂ = а₁ + d; а₃ = а₂ + d.

 А якщо необхідно знайти а₆₀ –?

                                    а₂ = а₁ + d;

                                    а₃ = а₁ + d + d = а₁ + 2d;

                                    а₄ = а₁ + d + d + d = а₁ + 3d;

а_n = а_{n - 1} + d – знаємо попередній член.

а_n = а ₁ + d(n – 1) – знаємо перший член а₁ і різницю d.

Приклади.

 № 1. Дана арифметична прогресія (а_n)  а_n = 2n² + 1. Знайти а₃, а₅, а_k+3.

Розв’язок: 

1) n = 3; а₃ = 2∙3² + 1 = 2∙9 + 1 = 18

2) n = 5; а₅ = 2∙5² + 1 = 2∙25 + 1 = 51

3) n = k+3; а_k+3 = 2∙( k+3)² + 1 = 2∙(k² + 6k +9) + 1 = 2k² +12k +18 +1 = 2k² +12k +19

№ 2. Дана арифметична прогресія (а_n)  а_n = (n – 1)(n + 4). а_n = 150, а_n = 8.

Чи буде 150 і 8 членом послідовності?

Розв’язок:

 Необхідно отримати натуральне число (N).

1)(n – 1)(n + 4) = 150; n² + 4n – n – 4 =150; n² + 3n – 4 –150 = 0; n² + 3n –154 = 0

            n₁ ∙ n₂ = – 154   (154:2∙7∙11 = 14∙11)      n₁ = 11

n₁ + n₂ = – 3                                             n₂ = –14 

Для квадратного рівняння підходять два кореня. Для даної задачі число повинно бути натуральне. Тобто, будемо використовувати  n = 11. Отже, а₁₁ = 150

2) (n – 1)(n + 4) = 8; n² + 3n – 8 = 0. Д = 9 +4∙12 = 57 – цілого значення з дискримінанта не отримаємо, отже корені рівняння будуть також не цілими. 8 не буде членом послідовності.

№ 3.  Дана арифметична прогресія – 38;– 34; – 30 ...

Скласти формулу n – го члена прогресії а_n.

Розв’язок: а_n = а_{n – 1} + d

а₁ = – 38; а₂ = – 34; d = – 34 – (– 38) = – 34 + 38 = 4

а_n = – 38 + 4(n – 1) = – 38 + 4n – 4 = 4n – 42

   № 4. Дана арифметична прогресія (а_n) .

а)  9,8;11; 12,2; 13,4 …  Знайти d – ? а₅ – ?

Розв’язок:  а₁ = 9,8; а₂ = 11.

d = а₂ – а₁ = 11–9,8 = 1,2     а₅ = а₁ + d(5 – 1) = а₁ + 4d =  9,8 +1,2∙4 = 9,8 + 4,8 = 14,6

б) – 7; – 4; – 1; + 2… Знайти d – ? а₅ – ?

Розв’язок:  а₁ = – 7; а₂ = – 4.

d = а₂ – а₁ = – 4 – + 7 = 3     а₅ = а₁ + d(5 – 1) = а₁ + 4d =  – 7+ 3∙4 = + 5.

№ 5. Дана арифметична прогресія (а_n) а₅ = 11; а₁₁ = – 7. Знайти: а₁ – ?

Розв’язок:  а₅ = а₁ + 4d; а₁₁ = а₁ + 10d

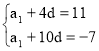  –       6d = – 18; d = – 18:6 = – 3;

  а₁ + 4d = 11; а₁ = 11– 4d = 11– 4∙(– 3) = 11+12  = 23

№ 4. Дана арифметична прогресія (а_n) а₃ + а₇ = 30; а₆ +  а₁₆ = 60. Знайти: а₁ – ? d – ?

                   + 

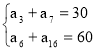
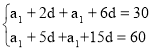
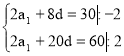
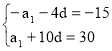6d = 15; d = 15:6 = 2,5; d = 2,5.

а₁ = 30 – 10d; а₁ = 30 – 10∙2,5 = 30 – 25 = 5; а₁ = 5.

Властивості арифметичної прогресії

 Кожен член арифметичної прогресії, починаючі з другого є середнім арифметичним рівновіддалених від нього членів прогресії.

    Що таке рівновіддалене? Наприклад, для а₃ рівновіддалені а₁ і а₅: а₁   а₃  а₅ .

Щоб з а₃ дійти до а₁ необхідно перейти через а₂. а₁ – це другий ліворуч.  Також а₅ – це другий праворуч. Для а₃ також будуть  рівновіддаленими а₂ і а₄   як сусідні.

                        а_n = (n – k; n + k кроків) – це застосовується для перевірки, чи є послідовність арифметичною прогресією. Або в деяких завданнях.

 Приклад. При якому  значенні х дані три числа будуть послідовними членами арифметичної прогресії : х² – 4; 5х + 3; 3х + 2.

 а₁ = х² – 4;   а₂ = 5х + 3;    а₁= 3х + 2

а₂ =  ; 5х + 3 = ;   10х + 6 = х² + 3х – 2;   х² – 7х – 8 = 0;

х₁ = – 1; х₂ = 8 – за теоремою коефіцієнтів.

Сума n – перших членів арифметичної прогресії

 Чому дорівнює сума  чисел від 1 до 100? Карл Гаусс  помітив, що сума

1 +100 = 101; 2 + 9 = 101; 3 + 98 = 101. Він зрозумів, що сума пари чисел буде 101. Якщо  чисел 100, то пар буде 50. 50 ∙ 101 = 5050.

 Отже, S_n = (a₁ + a_n) ∙. Зручний запис S_n = ∙n;  а_n = а ₁+ d(n – 1)

S_n = ∙n = ∙n.     S_n =  ∙n

№ 1. Дана арифметична прогресія (а_n), де а₁ = 9; а₇ = 15. Зайти суму семи перших  членів.

Розв’язок:  S_n = ∙n;   S₇ = ∙7 = 12∙7 = 84.

№ 2. Дана арифметична прогресія (а_n): – 8; – 6; – 4 …Знайти S₂₀ .

Розв’язок: S_n =  ∙n       а₁ =  – 8;  а₂ =  – 6    d = а₂ – а₁ = – 6 – (– 8)  = – 6 + 8 = 2

  S₂₀ =   ∙20 =  ∙20 =  (–16 +38)∙10 = 22∙10 = 220     

 № 1. Дана арифметична прогресія (а_n) S₆ = 39; S₁₄ = – 77. Знайти перший член і різницю.

  Розв’язок: S₆ =  ∙6 = 39;   S₆ =  (2а₁ + 5d) ∙3 = 39;    2а₁ + 5d  = 13

S₁₄ =  ∙14 = – 77;   S₁₄ =  (2а₁ + 13d) ∙7 =  – 77;         2а₁ + 13d =  – 11

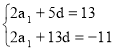–             – 8d = 24; d = 24: (– 8) = – 3; d = – 3

2а₁ + 5d  = 13; 2а₁ = 13 – 5d; 2а₁ = 13 – 5∙(– 3); 2а₁ = 13 + 15; 2а₁ = 28; а₁ = 28: 2 = 14.

а₁ = 14.

Завдання ЗНО на прогресії

ЗНО 2016 пробне

27.

Розв’язок: Розглянемо  арифметичну прогресію  (а_n), в якій перший член а₁ = 11 (кількість задач, розв’язаних за перший день), різниця d (величина, на яку щодня зростала кількість розв’язаних задач), сума перших дев’яти членів  S₉ =  315(кількість задач, розв’язаних за дев’ять днів). Для визначення дев’ятого члена прогресії а₉ (кількість задач, розв’язаних за дев’ятий день) скористаємося формуло суми n:  S_n = ∙n.

Тоді S_n9 = ∙9 ; ∙9 = 315; (а₁ + а₉)∙9 = 630;  а₉ = 70 – а₁; а₉ = 70 – 11 = 59.

Відповідь: за дев’ятий день учень розв’язав 59 задач.

ЗНО 2017 основна сесія

П’яте і четверте відрізняється на а₅ – а₄ = 3, отже d = 3, а = - 4 . а_n = а₁  + d(n – 1). а₅ – а₄ = 3

а₁₀ = а₁  + 3(10– 1). а₁₀ = - 4 + 3∙9 = - 4 + 27 = 23 Д.

ЗНО 2017 додаткова сесія

а₁ = - 21 – 1,5 = -22,5,  а_n = а₁  + d(n – 1).

а_n = -2,1 + 1,5(n – 1) = -2,1 +1,5 n – 1,5 = -22,5 +1,5 n. а_n < 0. -22,5 +1,5 n < 0,  1,5 n < 22,5,

n < 15 отже Б.

ЗНО 2018 пробне

а₃ = 2а₁; S₅ = 190; S_n =  ; а_n = а₁  + d(n – 1); а₃ = а₁  + 2d; а₃ = 2а₁ = а₁  + 2d;

2d = 2а₁ - а₁;  а₁ = 2d  ; = = = 4d∙5 = 190; 4d = 190:5;

4d = 38; d = 38:4 = 9,5.

ЗНО 2020 основна сесія

а_n = а₁  + d(n – 1).

а₂ = а₁  + d(2 – 1) = а₁  + d;  а₅ = а₁  + d(5 – 1) = а₁  + 4d

а₁  + d – (а₁  + 4d) = а₁  + d – а₁ – 4d = – 3d = 7,8; d = 7,8 : (– 3) = – 2,6.

а₃ = а₁  + d(3 – 1) = а₁  + 2d; а₁  + 2d = – 1,8; а₁  + 2 (– 2,6)= – 1,8; а₁  – 5,2= – 1,8;

а₁  =  5,2 – 1,8 = 3,4.

ЗНО 2020 додаткова сесія

а₂ –  а₆ = 7,2 , d – ?

а_n = а₁  + d(n – 1). а₂ = а₁  + d(2 – 1) = а₁  + d ; а₆ = а₁  + d(6 – 1) = а₁  + 5d.

Від більшого виразу віднімемо менший 

а₁  + d – (а₁  + 5d) = а₁  + d – а₁  – 5d = – 4d; – 4d = 7,2; d = 7,2 (– 4) = –1,8

а₄ = а₁  + d(4 – 1) = а₁  + 3d. а₁  + 3d = 0,7; а₁  + 3(–1,8) = 0,7; а₁  + (–5,4) = 0,7;

а₁  = 0,7+ 5,4; а₁  = 6,1.

ЗНО 2021 основна сесія

а₇ = 2,6∙7 – 7 = 18,2 – 7 = 11,2.

а₁ = 2,6 – 7 = – 4,4; а₄ = 2,6∙4 –7 = 3,4; а₄ – а₁ =3, 4 – (– 4,4) = 3,4  + 4,4 = 7,8.

а₄ – а₁ = 2,6∙4 – 7–2,6 + 7= 2,6(4 – 1) = 2,6∙3 = 7,8

ЗНО 2021 пробне

Незвичайне завдання.

S₆ = ∙6 = (5,2 – 4,8)∙3 = 1,2

S₄ = a₁ + a₂ + a₃ + a₄. S₃ = a₁ + a₂ + a₃; S₄ = S₃ + a₄ a₄ = S₄ – S₃.

S₄ = ∙4 = (5,2 – 3,2)∙2 = 4;   S₃ = ∙3 = ∙3 = 1,2 ∙3  = 4,2 

a₄ = 4 – 4,2 = – 0,2.

ЗНО 2021 демонстраційний

24

а_n = а₁  + d(n – 1); а₂ = а₁  + d(2 – 1) = а₁  + d;  а₄ = а₁  + d(4 – 1) =  а₁  + 3d.

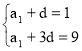, 2d = 8; d = 8:2; d = 4.

 а₁ + 4 = 1; а₁ = 1 – 4 = –3; d = 4.

S_n =  ∙ n; S₂₀ =   ∙20  = (– 6 + 4∙19)∙10  =(– 6 + 76)∙10 = 700.

НМТ 2022 демонстраційний варіант

Зошит 2

Розв’язок:  а₃ = 20; d = –3,2; S₆ – ?

S_n =  ∙ n; а_n = а ₁+ d(n – 1); а₃ = а ₁+ d(3– 1); а₃ = а ₁+ 2d; 20 = а ₁+ 2∙(– 3,2);

20 = а ₁– 6,4; а ₁ = 20 + 6,4; а ₁ = 26,4.

S₆ =  ∙ 6 = (52,8 – 16) ∙3 = 36,8∙3 = 110,4