Підсумкова контрольна робота з алгебри, 7 клас

Урок № ___                                                                                                     7 клас

Тема. Підсумкова  контрольна  робота

Мета: виявити якість та рівень засвоєння знань, умінь і навичок учнів за рік. Виявити недоліки в знаннях і навичках учнів. Виховувати зібраність, самовладання, самостійність.

Тип уроку: урок контролю навичок і вмінь.

Хід уроку

І. Органiзацiйний етап

Організація уваги учнів.

ІІ. Виконання контрольної роботи

Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.

У І частині  контрольної роботи запропоновано п’ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки один правильний. Завдання вважається виконаним правильно, якщо учень указав тільки одну літеру, якою позначений правильний варіант відповіді.

Правильна відповідь за кожне із завдань 1-5 – оцінюється одним балом.

ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв’язання повинно мати короткий запис рішення без обґрунтування. Правильне розв’язання кожного із завдань цього блоку оцінюється двома балами.

ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв’язання якого повинно мати розгорнутий запис рішення з обґрунтуванням. Правильне розв’язання завдання цього блоку оцінюється трьома балами.

Варіант 1

1. Спростіть вираз:   m − (n + m − p).

А) (2m – n − p); Б) (p − n);  В) (2m – n − p); Г) (n − p).

2. Виконайте дії:   .

А) 9;   Б) 0,9;  В) 1;   Г) 0,09.

3. Спростіть вираз:   .

А) ;  Б) −1;   В) ; Г) 1.

4. Розв’яжіть рівняння:   3у + 4,1 = у − 0,5.

А) 2,3;  Б) 0,9;  В) –2,3;  Г) –0,9.

5. Графік якої функції зображено на малюнку?

А) у = х − 2;          Б) у = −2 х;

В) у = −х;           Г) у = х + 1.

6. Доведіть тотожність: 

7. Розв’яжіть графічно систему рівнянь:  

8. Один сплав містить 10% цинку, а другий – 30% цинку. Скільки кілограмів кожного сплаву треба взяти, щоб отримати 400 т сплаву, який містить 25% цинку?

Варіант 2

1. Спростіть вираз:    3(x − y) + 3y.

А) 3x;   Б) (3x + 2y);  В) (3x + 6y); Г) (3x − 6y).

2. Запишіть одночлен у стандартному вигляді:   .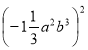

А) ;  Б) ;  В) ;  Г) .

3. Спростіть вираз:    .

А)  Б)   В) ;  Г) .

4. Розв’яжіть систему рівнянь:    .

А) ;  Б) ;   В) ;  Г) Розв’язку не існує.

5. Запишіть формулу для обчислення периметра і площі фігури ABCD, зображеної на малюнку.

А)   Б)

В)         Г) інша відповідь.

6. Знайдіть область визначення функції, яку задано формулою  .

7. Розв’яжіть рівняння:    +=2.

8. З двох розчинів солі − 10% і 15% − потрібно отримати 40 г 12% розчину. Скільки для цього потрібно взяти кожного розчину?

ІІІ. Підсумок уроку. 

Головним підсумком уроку є виконання (або невиконання) учнями завдань. Учні підводять підсумки своєї роботи на уроці: (впорався «+» чи не впорався «—» із завданнями уроку).

ІV. Домашнє завдання.

Опрацювати номери, які викликали труднощі.