Підсумковий урок алгебри в 9 класі по темі "Прогресії".

Прогресу без прогресій не буває! Автори проєкту: Ніценко Людмила Олександрівна, вчитель математики СЗОШ № 12 м. Хмельницького, учні 9 класу

Мета проєкту: Впровадження STEM – навчання на уроках математики. 2. Проєкт створено з метою перевірки якості засвоєння знань з теми “Арифметична та геометрична прогресіі”. 3. Проєкт спрямований на застосування знань про прогресії для розв'язування життєвих задач та використання знань з суміжних дисциплін. 4. Проєкт спрямований на створення ситуації успіху та розвиток навичок спілкування та співпраці.

План реалізації проєкту Проєкт реалізовується у формі уроку- конференції та створення учнівських презентацій. Учні класу були об'єднані в 5 груп та отримали відповідні завдання.

“ Предмет математики настільки серйозний, що корисно не упускати можливості робити його трохи цікавим” (Паскаль)

* *

* * Перевіримо «фундамент знань»: 1. Що таке арифметична прогресія? 2. Що таке геометрична прогресія? 3. Що спільного в означеннях, чим вони відрізняються? 4. Яке число називається різницею арифметичної прогресії? 5. Яке число називається знаменником геометричної прогресії?

Означення арифметичної прогресії Означення геометричної прогресії Формула n-го члена арифметичної прогресії Формула n-го члена геометричної прогресії Різниця арифметичної прогресії Знаменник геометричної прогресії Сума n-перших членів арифметичної прогресії Сума n-перших членів геометричної прогресії Властивість членів арифметичної прогресії Властивість членів геометричної прогресії 1 2 3 4 5 6 7 8 9 10

* * Код відповіді 372 186 549 10

Для проведення уроку учнями розроблені наступні матеріали * * 1. Презентація “Історичні відомості про прогресії”. 2. Презентація “Від деяких задач на прогресії віє далекою давниною”. 3. Презентація “Арифметична та геометрична прогресії в задачах фізики”. 4. Презентація “Прогресії в задачах біології .” 5. Презентація “Арифметична прогресія в літературі”.

Історичні відомості про прогресії

Слово “прогресія” походить від латинського слова “progressio” і означає “рух уперед” (як і слово “прогрес”). Уперше цей термін як математичний вживається у працях римського вченого Боеція (V - VIст.).

Прогресії як часткові види числових послідовностей, трапляються в папірусах ІІ тисячоліття до н. е.

Найдавнішою задачею, пов’язаною з прогресіями, вважають задачу з єгипетського папірусу Ахмеса: “Нехай тобі сказали: розділи десять мір ячменю між 10 чоловіками так, щоб різниця між кожним чоловіком і його сусідом становила 1/8 міри ячменю ”.

У папірусі подається не тільки текст задачі, але й пропонується правило для обчислення частки першої з десяти осіб.

Задача із папірусу Рінда “Є 7 будинків, в кожному будинку по 7 котів, кожен кіт з’їдає 7 мишей, кожна миша з’їдає по 7 колосків ячменю, кожен колосок, якщо посіяти зерно з нього, дає 7 мір ячменю. Знайти суму загального числа будинків, котів, мишей, колосків і мір”.

АНГЛІЯ XVIII століття В XVIII ст. в англійських підручниках з’явилися позначення арифметичної і геометричної прогресії. Арифметична Геометрична

У нас задачі на прогресії вперше зустрічаються в одній з найдавніших пам’яток руського права, в “Руській правді”, складеній при Ярославі Мудрому в ХІ столітті.

Там є стаття, присвячена обчисленню приплоду від 22 овець за 12 років, при умові, що кожна вівця щорічно приносить одну овечку і одного барана.

Давно неабиякою популярністю користується задача-легенда, яка належить до початку нашої ери. Індійський мудрець, який придумав гру в шахи, попросив за свій винахід у раджі, на перший погляд, скромну винагороду: за першу клітинку шахової дошки 1 пшеничне зернятко, за другу – 2, за третю – 4 і т. д. – за кожну наступну клітинку вдвічі більше, ніж за попередню.

Складемо послідовність чисел 1, 2, 4, 8, 16 … Дана послідовність є геометричною b1 = 1, q = 2, n = 64. S64 - ? Загальна кількість зерен, яку попросив винахідник, дорівнює S64=264-1

Багатий раджа був приголомшений, коли дізнався, що він не в змозі задовольнити це “скромне” бажання. Справа в тому, що значення цього виразу дорівнює 18446744073709551615. Для того, щоб зрозуміти, наскільки величезним є це число, уявимо, що зерно зберігають у коморі площею 12 га. Її висота була б більшою за відстань від Землі до Сонця.

Від деяких задач на прогресії віє далекою давниною.

Задача Феофана Прокоповича Якась людина має багато коней, і всім їм різна ціна. Найгірший кінь коштує 4 золотих, а найкращий 55 золотих, і ціна від одного до другого коня весь час піднімається на 3 золотих. Скільки ж усього було коней?

Розв’язання d=3 n-? 55=4+3(n-1) n=18 Відповідь: було 18 коней.

Задача з “ Теоретичного і практичного курсу чистої математики’’ Ю. Войтяховського Воякові дано винагороду: за першу рану – 1 копійка, за другу – 2 копійки, за третю – 4 копійки і т.д. Після обрахунку виявилося, що вояк отримав винагороду в сумі 655 рублів 35 копійок. Питання: чому дорівнює кількість його ран?

Розв’язання Нехай число ран n, тоді 1+2+4+8+… =65535 1,2,4,8… - геометрична прогресія, тоді q=2. Відповідь: вояка мав 16 ран.

У газеті, що була видана у 1914 р., описувалася справа, яка відбулося у місті Новочеркаську, про продаж отари, що має 20 овець, за такими умовами: за першу вівцю слід заплатити 1к., за другу – 2к., за третю – 4к. і т.д. У яку суму обійдеться вся отара?

Вартість овець, про які йдеться в задачі, є сумою 20 членів геометричної прогресії, перший член якої b1=1, а знаменник q=2. Тоді 1048575 к. = 10485 крб. 75 к Відповідь. 10485 крб. 75 к.

Задача із “Арифметики” Магніцького

Розв’язання Відповідь. усі чарки важать 462 лота. d=4,

Задача із “Арифметики ” Магніцького Продавець продав коня за 156 крб. Але покупець, придбавши коня, передумав і повернув його господарю, кажучи:"Нема мені користі купувати за таку ціну коня, який таких грошей не вартий". Тоді продавець запропонував інші умови: "Якщо ціна за коня дуже висока, то купи лише цвяхи для його підков, а коня одержиш безплатно на додачу. Цвяхів у кожній підкові 6. За перший дай мені всього 1/4 к., за другий – 1/2 к., за третій - 1к. і т. д." Покупець, спокусившись низькою ціною та бажаючи безплатно придбати коня, прийняв умови, думаючи, що за цвяхи доведеться заплатити не більше 10 крб. На скільки покупець проторгувався?

Розв’язання Складемо послідовність чисел Дана послідовність є геометричною з q=2, n=24 (4 підкови по 6 цвяхів дорівнює 24) Отже, покупець проторгувався на 42000-156=41844 (крб)

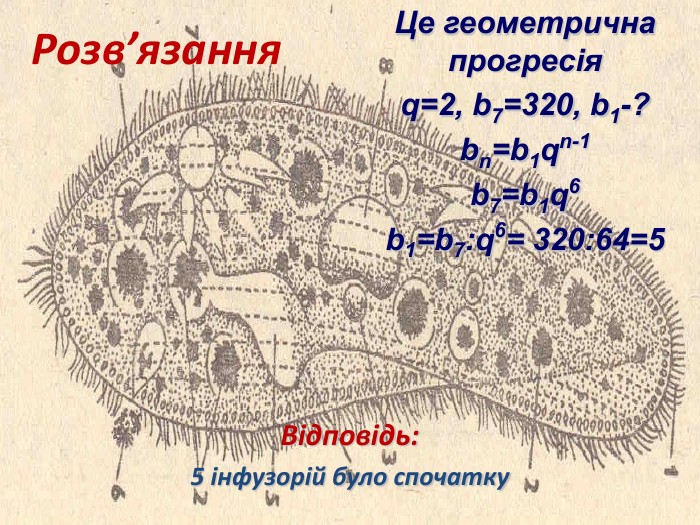
В біології прогресії пов’язані з такими темами, як розмноження, поділ клітин, формені елементи крові та інші. Неможливо розв’язати біологічні задачі з даних тем, не використавши знання про прогресії. За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються прогресивно або регресивно.

За сприятливих умов за 1 хв кожна з бактерій поділяється навпіл. Визначити кількість бактерій, народжених однією бактерією за 7 хв. Розв'язання: Кількість бактерій зростає за геометричною прогресією: b1=1;q=2; n=7. S7=127.

Скільки інфузорій було спочатку, якщо після 6-го поділу їх стало 320? Інфузорії туфельки розмножуються поділом на 2 частини

Розв’язання Відповідь: 5 інфузорій було спочатку Це геометрична прогресія q=2, b7=320, b1-? bn=b1qn-1 b7=b1q6 b1=b7:q6= 320:64=5

Задача №3

Задача №1

a1=12, d=-2, an=0 an=a1+d(n-1) 0=12-2(n-1) n=7 S7=42м Відповідь: гальмівний шлях автомобіля 42м.

Потяг пройшов за першу хвилину 620м, а за кожну наступну хвилину – на 80м менше, ніж попередню. Яку відстань пройшов потяг за восьму хвилину?

Тіло, яке вільно падає, проходить за першу секунду 4,9м, а за кожну наступну – на 9,8м більше, ніж за попередню. Встановити, скільки секунд падатиме тіло з висоти 1960м?

Розв’язання a1=4,9, d=9,8, Sn=1960 n=25 Відповідь: 25с падатиме тіло з висоти 1960м.

Задача №4 Після кожного руху поршня розріджувального насоса з посудини забирається 5% наявного в ній повітря. Визначте тиск повітря в середині посудини після десяти рухів поршню, якщо початковий тиск був 760мм рт.ст.

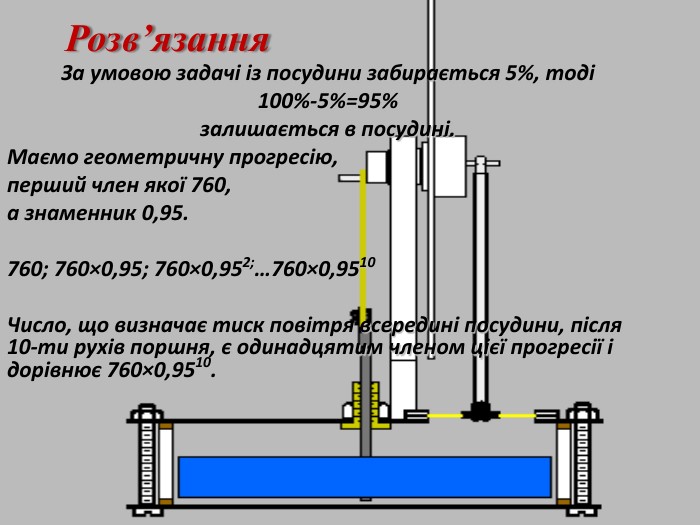
Розв’язання За умовою задачі із посудини забирається 5%, тоді 100%-5%=95% залишається в посудині. Маємо геометричну прогресію, перший член якої 760, а знаменник 0,95. 760; 760Ч0,95; 760Ч0,952;…760Ч0,9510 Число, що визначає тиск повітря всередині посудини, після 10-ти рухів поршня, є одинадцятим членом цієї прогресії і дорівнює 760Ч0,9510. •

Арифметичну прогресію можна зустріти в літературі. Згадаємо віршові розміри: ямб, хорей, дактиль, амфібрахій, і анапест. Відмінність між ними в кількості стоп і в різних розташуваннях наголошених складів вірша.

ЯМБ Ямб – двоскладова стопа з наголосом на другому складі 2; 4; 6; 8;… Номери наголошених складів утворюють арифметичну прогресію с першим членом 2 та різницею арифметичної прогресії 2.

Ста/рі/ ду/би, спа/си/бі/ вам /за /о/сінь, за/ від/лі/та/ння ра/до/сті /і /птиць. Ще/, пев/но, я/ за/тур/ка/на не/ зов/сім, Що/ чу/ю шур/хіт/ кня/жих баг/ря/ниць (Ліна Костенко) П’ятистопний ямб

ХОРЕЙ Хорей – двоскладова стопа з наголосом на непарних складах вірша. Номери наголошених складів утворюють арифметичну прогресію, перший член якої дорівнює 1, а різниця дорівнює 2: 1, 3, 5, 7, 9…

Дощ/ по/лив/, і /день/ та/кий/ по/ли/в’я/ний/, Все/ бли/щить/, і/ лю/ди/ як/ но/ві/. Лиш/ ді/док/ ста/ре/сень/кий/, кро/пи/в’я/ний/, Блис/кав/ки/ ви/зби/ру/є/ в тра/ві/. (Ліна Костенко) П’ятистопний хорей

ДАКТИЛЬ Дактиль –трискладова стопа з наголосом на першому складі. Номери наголошених складів утворюють арифметичну прогресію, перший член якої дорівнює 1, а різниця дорівнює 3: 1, 4, 7, 10…

В рай/ду/гу/ чай/ка/ ле/ті/ла/. Хма/ра/ спли/ва/ла/ на/ схід/. Мо/же/ б, і/ ти/ за/хо/ті/ла/ Чай/ці/ по/да/ти/ся/ вслід/? Сон/це/ на/ за/хо/ді/ впа/ло/. Рай/ду/га/ згас/ла/ в ім/лі/. Тем/но/ і хо/лод/но/ ста/ло/ На/ не/спо/кій/ній/ зем/лі/... (Л. Первомайський) Тристопний дактиль

Продовжи фразу: Сьогодні на уроці я: - дізнався ... - навчився ... - повторив ... - закріпив ... Результатом своєї власної роботи вважаю, що я …