План-конспект уроку на тему "Відстані у просторі"

План-конспект уроку

Тема: Відстані у просторі

 

Мета:

 - узагальнити та систематизувати знання учнів про відстані між основними геометричними фігурами в просторі;

- сприяти розвитку в учнів просторової уяви, логічного мислення та навичок самостійності;

- удосконалювати культуру математичного запису та мови.

 

Тип уроку:

- урок формування умінь і навичок розв’явування задач на знаходження відстаней у просторі

 

 Обладнання: комп’ютер, телевізор, супроводжуюча презентація, картки-завдання, підручник, дидактичний матеріал, моделі куба

 

ХІД УРОКУ

І. Організаційний етап

 Психологічне налаштування на роботу на уроці

ІІ. Актуалізація опорних знань

1. Фронтальне опитування

(правильна відповідь -0,5 бали) – 4 бали

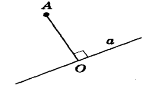
1) Між якими основними геометричними фігурами можливе знаходження відстані?           

2) Як знаходимо відстань від точки до:

а) точки;

б) прямої;

в) площини?

3) Як знаходимо відстань від прямої до:

а)  паралельної прямої;

б) мимобіжної прямої;

в)  площини?

4) Як знаходимо відстань між паралельними площинами?

 

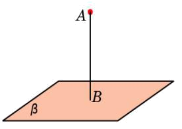
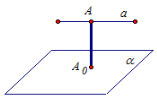
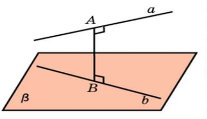
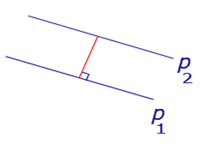
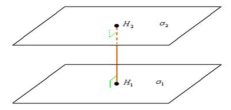
2. Встановить відповідність між назвою відстані ( № ) та малюнком ( Буква ) Самоперевірка за готовими відповідями (правильна відповідь -0,5 бали) – 3,5  бали

№	Назва	Буква	Малюнок
1	Між площинами	А
2	Між паралельними прямими	Б
3	Між точками	В
4	Між мимобіжними прямими	Г
5	Між точкою і площиною	Д
6	Між прямою і площиною	Е
7	Між точкою і прямою	Є

 

Відповіді:

1	2	3	4	5	6	7
Є	Е	А	Д	В	Г	Б

 

 

ІІІ. Формування практичних умінь і навичок розв’язування задач

1. Виконання вправ за готовими малюнками  для учнів початкового рівня навчальних досягнень (виконання в парах) Взаємоперевірка за готовими відповідями (№1 - кожна правильно закреслена відповідь - 0,5 бали – 1,5  бали;   №2 - кожна правильно обведена відповідь – 0,5 бали)

 

 

 

 

Картка-завдання

Відповіді:

№1	Закреслені:  А1В;    D1B;    D1С
№2	Обведені  -  КР

 

2. Виконання тестових завдань для учнів середнього та достатнього рівнів навчальних досягнень правильно розв’язана задача  - 3 бали

 

Варiант  1

З точки A до площини α проведено похилу AB. Знайдiть довжину проекцiї цiєї похилої на площину α, якщо AB =26 см, а вiдстань вiд точки A до площини α  дорiвнює 10 см.

А) 24 см;  Б) 16 см;  В) 25 см;   Г) 576 см.

 

Варiант  2

ABCD— квадрат зi стороною 4 см. З точки B проведено перпендикуляр BM до площини квадрата. Знайдiть  вiдстань вiд точки M до площини квадрата, якщо вiдстань вiд точки M до вершини A дорiвнює 5 см.

А) 5 см;   Б) 34 см;   В) 3 см;   Г) 9 см.

 

Варiант  3

Через точку O перетину дiагоналей квадрата проведено перпендикуляр KO до площини квадрата. Знайдiть вiдстань вiд точки

K до сторін квадрата, якщо сторона квадрата дорiвнює 10 см, а вiдстань вiд точки K до площини квадрата дорівнює 12см.

А) 5 см;   Б) 13 см;   В) 26 см;    Г) 169 см.

 

Варiант 4

З точки M до площини α проведено похилу MN. Знайдiть довжину похилої, якщо довжина її проекцiї на площину α дорiвнює 8 см, а точка M вiддалена вiд площини α на 6 см.

А) 10 см;     Б) 6 см;     В) 100 см;    Г) 50 см.

Варiант  5

ABCD— квадрат, дiагональ якого дорiвнює 5 см. З точки B проведено перпендикуляр BM до площини квадрата. Знайдiть вiдстань вiд точки M до площини квадрата, якщо вiдстань вiд точки M до вершини D дорiвнює 13 см.

А) 13 см;    Б) 15 см;     В) 10 см;    Г) 12 см.

 

Варiант 6

Через точку O перетину дiагоналей квадрата проведено перпендикуляр KO до площини квадрата. Знайдiть сторону квадрата,

якщо вiдстань вiд точки K до площини квадрата дорiвнює 12 см, а до сторiн квадрата — 20 см.

А) 16 см;   Б) 20 см;    В) 32 см;    Г) 18 см.

 

3. Колективне розв'язування задачі

* Рівні прямокутники ABCD і ABC₁D₁ лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD₁ і С₁D , якщо АВ=15 см, ВС=20 см.

 

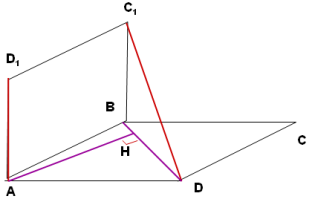
Розв’язання

Оскільки D₁A і C₁В – перпендикуляри до прямої  перетину двох перпендикулярних площин, то D₁A (АВС), С₁В (АВС).

Побудуємо ортогональні проекції прямих AD₁ і С₁D на площину АВС. Проекціями є відповідно точка А та пряма BD. Шукана відстань дорівнює висоті АН прямокутного трикутника ABD (A=90⁰)

Оскільки за теоремою Піфагора ВD=25 см,  то за властивістю висоти прямокутного трикутника, що вона дорівнює відношенню добутку катетів до гіпотенузи, маємо

Відповідь: 12 см

 

IV. Підсумок уроку

1. Усно:

ABCDA₁B₁C₁D₁  – прямокутний паралелепіпед.    Вказати відстані між а) площинами:  ABC  і  A₁B₁С₁;  AA₁B₁  і  DD₁C₁  

б) прямими :    AA₁  і  DС;  BC₁  і  DD₁.

  2. Рефлексія  

4-що!
1. Що навчились?
2. Що засвоїли?
3. Що повторили?
4. Що ще треба навчитись?
 

V. Оцінювання навчальних досягнень учнів впродовж уроку учні виставляють бали собі в зошити, викладач сумарний бал виставляє вибірково

VІ. Домашнє завдання

1. Повторити поняття кута, його властивостей, видів

2⁰. Відстань від точки М до сторін квадрата дорівнює 13 см. Знайдіть відстань від точки М до площини квадрата, якщо сторона квадрата дорівнює 10 см.

А) 8 см;    Б) 11 см;    В) 12 см;     Г) 15 см.