План-конспект уроку з геометрії для 10 класу на тему "Властивості паралельних прямих"
Практична компетентність передбачає, що випускник ПТНЗ вміє будувати і досліджувати найпростіші математичні моделі реальних об'єктів, процесів і явищ, задач, пов'язаних із ними, за допомогою математичних об'єктів, відповідних математичних задач.
Мета уроку: Домогтися засвоєння властивостей паралельних прямих; сформувати вміння застосовувати їх при розв'язуванні задач.План конспект уроку
Тема: Властивості паралельних прямих
Мета: Домогтися засвоєння властивостей паралельних прямих; сформувати вміння застосовувати їх при розв’язуванні задач.
Учні повинні знати: Властивості паралельних прямих
Обладнання: Стереометричний набір, моделі тетраедра і куба, дидактичний матеріал, підручник, таблиця «Паралельність прямих і площин у просторі».
Тип уроку: засвоєння нових знань і вмінь
Хід уроку
І. Організаційна частина
Превірка присутніх
Психологічне налаштування учнів на роботу на уроці
ІІ. Перевірка домашнього завдання
Перевірка задачі ( №2*: Доведіть, що якщо прямі АВ і CD мимобіжні, то й прямі AC і BD також мимобіжн) за зразком на дошці
|
Доведення |
Малюнок |
|
Нехай АС і BD не є мимобіжними
що суперечить умові. Висновок: прямі AC і BD також мимобіжні. |
|
ІІІ. Актуалізація опорних знань
- Чи правильне твердження: «Оскільки прямі a і b лежать у різних площинах і не перетинаються, то вони мимобіжні»?
- Точки К, М, Р, Н – середини ребер куба (рис. 1). Чи перетинаються прямі КМ і РН?
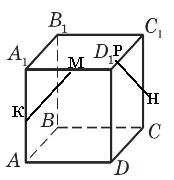 Яке взаємне розміщення прямих AD1 і A1B (рис.2)? Відповідь поясніть.
Яке взаємне розміщення прямих AD1 і A1B (рис.2)? Відповідь поясніть.
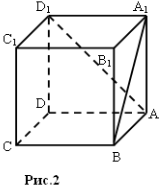
![]()
ІV. Мотивація вивчення теми. Постановка проблемної задачі.
Задача. Прямі a і b перетинаються. Доведіть, що всі прямі, які паралельні прямій b і які перетинають пряму a, лежать в одній площині.
Розв’язуючи задачу, ми використовуємо аксіому планіметрії ( через точку площини проводимо пряму, паралельну даній), тому виникає запитання: а чи працює ця аксіома в просторі? Скільки існує в просторі прямих, паралельних
даній, що проходять через дану точку? Виникає проблема і розв’язати її допоможе …
V. Оголошення теми уроку
VІ. Вивчення нового матеріалу
Учні записують теорему в зошит.
Теорема (основна властивість паралельних прямих у просторі) Через точку, яка лежить на прямій, у просторі можна провести пряму, паралельну даній прямій, і до того ж тільки одну.
Доведення теореми проводиться у формі бесіди, яка супроводжується записами на дошці та в зошитах у вигляді таблиці.
|
Запитання викладача |
Записи |
|
1. Чи можна провести площину через точку А і пряму a? 2. Чи можна провести в площині a через точку А пряму a1// a?
3. У площині a не існує інших прямих, таких, що проходять через точку А і паралельні a . Чи існує пряма b// a1, А |
1. Існує a, (a,А)
2. Існує a1// a, a1
3. Будь-яка пряма b,
4. Висновок: a1// a |
VІІ. Контроль та корекція первісного сприйняття матеріалу
Виконання тестових завдань
Варiант 1
|
1) A,B, C,D—точки, якi не лежать в однiй площинi. Яке з наведених тверджень у цьому випадку правильне? |
|||
|
А) Прямi AB i CD можуть перетинатися |
Б) Прямi AB i CD можуть бути паралельними |
В) Прямi AB i CD мимобiжнi
|
Г) Прямi AB i CD лежать в однiй площинi |
|
2) Визначте взаємне розмiщення прямих a i b, якщо пряма a лежить у площинi α, а пряма b перетинає площину α у точцi, яка не належить прямiй a. |
|||
|
А) Паралельнi |
Б) перетинаються |
В) мимобiжнi |
Г) збігаються |
|
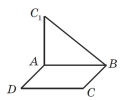
3) Якщо паралелограм ABCD i трикутник ABC1 лежать у рiзних площинах (див. рисунок), то яке твердження правильне?
|
|||
|
А) Прямi AC1 i BD перетинаються |
Б) Прямi C1B i AD можуть бути паралельними |
В) Прямi CC1 i AD мимобiжнi |
Г) AC1 i DB можуть бути паралельними |
|
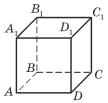
4) ABCDA1B1C1D1 — куб (див. рисунок). Через якi з наведених прямих неможливо провести площину?
|
|||
|
А) A1C1 i AC |
Б) A1B1 i DC |
В) BB1 i DD1 |
Г) AB i C1C |
Варiант 2
|
1) Укажiть правильне твердження |
|||
|
А) Якщо двi прямi не перетинаються, то вони обов’язково паралельнi.
|
Б) Якщо двi прямi не мають спiльної точки, то вони обов’язково мимобiжнi. |
В) Якщо пряма a лежить у площинi α, а пряма b— у площинi β, то прямi a i b обов’язково мимобiжнi. |
Г) Якщо двi прямi лежать в однiй площинi, то вони не мимобiжнi.
|
|
2) Визначте взаємне розмiщення прямих a i b, якщо площина α мiстить пряму a i перетинає пряму b у точцi, яка не належить прямiй a. |
|||
|
А) Перетинаються |
Б) мимобiжнi |
В) паралельнi |
Г) збігаються |
|
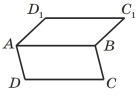
3) Якщо паралелограми ABCD i ABC1D1 лежать у рiзних площинах (див. рисунок), то яке твердження неправильне?
|
|||
|
А) Прямi AC1 i DB мимобiжнi |
Б) прямi DD1 i AB перетинаються |
В) прямi DC i D1C1 паралельнi |
Г) прямi AD i C1B мимобiжнi |
|
4) ABCDA1B1C1D1 — куб (див. рисунок). Через якi з наведених прямих неможливо провести площину?
|
|||
|
А) AA1 i BC |
Б) A1B1 i C1C |
В) AB1 i CD1 |
Г) A1C1 i DC |
VІІІ. Підсумок уроку
1.
|
Укажіть паралельні прямі на рисунках |
||
|
|
|
|
2. Рефлексія
На уроці я
• дізнався …
• зрозумів…
• навчився…
• найбільший мій успіх…
• найбільші труднощі я відчував…
ІХ. Оцінювання навчальних досягнень учнів відповідно до Критеріїв оцінювання
Х. Домашнє завдання
Самостійна робота
 І варіант
І варіант
|
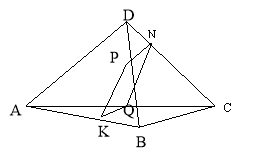
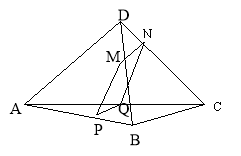
1. Точки M, N, P, Q - середина відрізків BD, CD, AB, AC відповідно, AD- 16см, АС- 18см. Знайти периметр чотирикутника MNPQ.
|
|
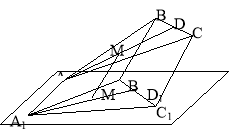
Через вершини трикутника АВС і точку М – середину медіани AD цього трикутника проведено паралельні прямі, які перетинають
площину відповідно. Знайти довжину відрізка ММ1, якщо АА1=3см, ВВ1=8см, СС1=6 см. |
ІІ варіант
BD, CD, AB, AC відповідно, AD- 20см, АС- 16см. Знайти периметр чотирикутника KPNQ.
|
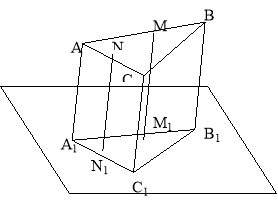
Через його вершини і середини M і N відповідно сторін АВ і АС проведено паралельні прямі, які перетинають
площину Знайти довжину відрізків ВВ1 і СС1, якщо АА1=9см, NN1=8см, ММ1=10см.
|


про публікацію авторської розробки
Додати розробку