План уроку "Властивості логарифмів"

ПЛАН УРОКУ

 

Дата «____»_________________ 202_ р.

Предмет:   Алгебра і початки аналізу

Тема:  Показникова і логарифмічна функції 

Тема уроку:  Властивості логарифмів

Мета уроку:

-         навчальна:  вивчити основні властивості логарифмів та сформувати вміння й навички їх застосування до розв’язування вправ;

-         розвиваюча: розвивати творче мислення, обчислювальні навички, вміння аналізувати, робити самостійні висновки;

-         виховна: виховувати інтерес до математики, почуття відповідальності, культуру діалогу, впевненість при прийнятті рішень, уміння створювати умови для цілісного сприйняття загальної картини та орієнтуватись в нестандартних ситуаціях

Тип уроку: урок вивчення нового матеріалу

Вид уроку: лекція  з елементами пошукового практикуму та тестами у форматі ЗНО

Методи: словесні (діалог, монолог), наочні, частково пошукові, евристичні, практичні

Дидактичне забезпечення: робочий зошит з теми «Властивості логарифмів», презентація викладача

Обладнання: ноутбук, проектор, екран

                                                                    «Щоб. дійти до мети, треба

                                                                      перш за все йти…»

                                                                                                    Оноре де Бальзак

Хід уроку

І. Організаційний момент.

Повідомлення теми і мети уроку. 

ІІ. Актуалізація опорних знань

Вправа: «Зарядка для розуму» ( учні відповідають ланцюжком)

1) Вставте пропущені слова:

Логарифм числа b за основою а — це  (показник степеня), до якого треба піднести а, щоб отримати b.

log_a b = n, ⇔ aⁿ=b (b >0; a >0;  a ≠ 1)

2) Виберіть вірну відповідь:

Який з виразів є логарифмом числа х за основою а?

       A )  log_x a; Б) log_a x; В) x lg a; Г) lg ^a x

3) Вставте пропущені слова та вирази:

  а) Логарифм за основою 10 називають (десятковим)  і позначають lg b.

б) Логарифм за основою e називають (натуральним) і позначають ln x.

(e – ірраціональне число, e ≈ 2,7)

4) Виберіть вірну відповідь:

Яка рівність вірна?

А ) lg 1 =2; Б) ln 1 = e; В) lg = - 2; Г) ln = 0

 

5) Виберіть вірну відповідь:

Яку з рівностей називають основною логарифмічною тотожністю?

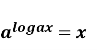А) ; Б) ; В) Г)

6) Знайди помилку:

 = = = 12

Вірно: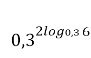= 6²=36

 

 

ІII. Мотивація навчальної діяльності

      Для чого взагалі потрібні логарифми? Яка від них практична користь?

  Мабуть, найкраще відповів на ці питання знаменитий математик, фізик і астроном П’єр-Симон Лаплас (1749-1827). На його думку, винахід такого показника, як логарифм, немов подвоює життя астрономів, скорочуючи обчислення кількох місяців в працю кількох днів. Деякі на це можуть відповісти: мовляв, любителів таємниць зоряного неба порівняно небагато, а іншим-то людям що дають логарифми? Говорячи про астрономів, Лаплас мав на увазі, перш за все, тих, хто займається складними обчисленнями. А винахід логарифмів дуже полегшив цю роботу.

      Отже, логарифми потрібні для спрощення важких обчислювань.  Завдяки властивостям логарифмів множення можна замінити простим додаванням, ділення – відніманням, а добування кореня і  піднесення до степеню можна перетворити у множення та ділення.

Логарифми в житті людини

          Властивості будови слухового апарату людини відповідає властивостям логарифмічної функції. Тому діапазон звуків, що сприяє вухо, низький – від шелесту листя до гуркоту грому. Досліди показали, що організм ніби «логарифмує» отримані ним подразнення, тобто величина відчуття  приблизно пропорційна десятковому логарифму величини подразнення. Шкідливий вплив промислових шумів на здоров'я  і продуктивність праці робітників спонукало виробити прийоми точної числової оцінки гучності шуму, які опираються на властивості логарифмів.

           Музиканти рідко захоплюються математикою, хоча зустрічаються з нею набагато частіше, ніж самі про це підозрюють. Вони грають на «логарифмах». І дійсно, так звані ступені частот звукових коливань є логарифми за основою 2.

Під час будівництва ставків необхідно враховувати кількість води, що буде прибувати у ставок у період повені. Розрахунки проводяться за допомогою логарифмів. У сільському господарстві також не обійшлося без логарифмів. Адже вагу телят одчислюють за допомогою логарифмів.

Відомо, що, консервуючи овочі, важливо знати кислотність розчину, а, знаючи  кислотність, можна визначити концентрацію іонів водню. Це можна зробити за допомогою логарифмічних рівнянь, використовуючи десяткові логарифми.

 Об‘єм легенів можна виразити формулою:

f(x) =

Де х – вік людини у роках

(х > 10),

f(x) - об‘єм легенів у літрах.

Розраховано, що найбільший об‘єм легенів має двадцятирічна людина

(≈ 5,4 л)

IV. Сприйняття й усвідомлення нового матеріалу

Допоміжним засобом є презентація викладача, створена у програмі Power Point (ілюстративний матеріал до уроку, перевірка виконаних завдань).

Учні працюють в робочих зошитах.

Пояснення і осмислення навчального матеріалу відбувається за допомогою інтерактивних методів: виконується вправа : «Знайди помилку»,  проводяться пошуковий практикум і тест-контроль, розв’язуються задачі-тести у форматі ЗНО.

Лекція викладача з елементами бесіди та тестових питань

 у форматі ЗНО.

Теоретичні відомості

Властивості логарифмів:
Для будь-якого a >0;  a ≠ 1; x > 0; y >0
1) log_a 1 = 0;

 

2) log_a a = 1

Ці рівності випливають із співвідношень: а⁰ = 1, а¹ = а

 

Наприклад:

1) log₉ 1 = 0, оскільки 9⁰ = 1;

2) log₉ 9 = 1, оскільки 9¹ = 9

 

 

Теоретичні відомості

Властивості логарифмів: Для будь-якого a >0;  a ≠ 1; x > 0; y >0
3) log_a (xy) = log_a x + log_a y

Наприклад:    Обчисліть: lg20 + lg5 = lg100 =2

 

 Теоретичні відомості

Властивості логарифмів: Для будь-якого a >0;  a ≠ 1; x > 0; y >0

4) log_a  = log_a x – log_a y

Наприклад:    Обчисліть: log₁₂ 48 – log₁₂ 4 = log₁₂ = log₁₂12 =1

Вправа: «Знайди помилку»:

1.     log₃₆ 2 + log₃₆ 18 = log₃₆ (2+18) = log₃₆ 20

Вірно: log₃₆ (2∙18) = log₃₆ 36 = 1

2.     54 – 2 = (54-2) = 52

Вірно: 54 – 2   27 - 3

 

Теоретичні відомості

Властивості логарифмів: Для будь-якого a >0;  a ≠ 1; x > 0
5) log_a x ⁿ = n log_a x

Наприклад:    log₃ 81= log₃3⁴ = 4 log₃3=4

ЗНО не за горами (завдання  у форматі ЗНО)

Обчисліть значення виразу:

log₃45 + log₃900 – log₃500 = log₃ = log₃ (9∙9) = log₃81 = log₃3⁴ =

= 4 log₃3 =4∙1=4

 

 

 

Теоретичні відомості

Властивості логарифмів: Для будь-якого a >0;  a ≠ 1; x > 0
6) x =

Наприклад :== =

ЗНО не за горами (завдання  у форматі ЗНО)

Обчисліть:=== - = - ∙1= -

 

Теоретичні відомості

Властивості логарифмів: Для будь-якого a >0;  a ≠ 1; b > 0; c >0; c ≠ 1
7) Формула переходу до іншої основи:

 log_a b =

Наприклад :

Обчисліть: log₃₂64 = = = = = 1,2

ЗНО не за горами (завдання  у форматі ЗНО)

Обчисліть: log_b a, якщо log₃ a = 8, log₃ b = 5

Розв’язання:

Перейдемо до основи 3 за формулою: log_a b =

log_b a = = =1,6

 

Теоретичні відомості

Властивості логарифмів: Для будь-якого a >0;  a ≠ 1; b > 0; b ≠ 1

8) Формула переходу від основи a до b:

log_a b =

 

Наприклад :

Обчисліть: = = 7

 

ЗНО не за горами (завдання  у форматі ЗНО)

Обчисліть значення виразу:  log_a 500 – log_a 4, якщо log₅ a =

Розв’язання: log_a500 – log_a4 = log_a = = log_a125 = log_a = 3 ∙   = 3 ∙ =

= 3∙4 = 12

 

Теоретичні відомості

Властивості логарифмів: Для будь-якого b >0; d > 0; a > 0; a ≠ 1 c >0; c ≠ 1

9) log_a b ∙ log_c d = log_c b ∙ log_a d

Наприклад :

Обчисліть:

log₄ 3∙lg4∙log₉ 10 = log4 4∙lg 10∙log9 3 =1∙1∙ = log₃3 =

ЗНО не за горами (завдання  у форматі ЗНО)

Обчисліть: log₃4∙log₄5∙log₅7∙log₇81 = log₃81∙log₄4∙log₅5∙log₇7 = log₃= 4 log₃3 =

= 4∙1= 4

 

Пошуковий практикум (додатково)

завдання з демонстраційного варіанту ЗНО 2021 р.

Обчисліть значення виразу:

 

  = =  = = - = - 0,75

 

 

 

Пошуковий практикум (додатково)

1) Обчисліть значення виразу: log₅ 49 + 2log₅  

 

      2) Знайти значення виразу:

 

      3) Обчисліть , якщо = 7

 

А	Б	В	Г	Д
	2	3		4

 

V. Осмислення нового матеріалу.

Тест-контроль (кожна вірна відповідь – 2 бали)

 Якщо ви набираєте :

1 - 4 бали, то рівень засвоєння низький, 5-6 – середній, 7-9 – достатній,

10-12 – високий

1) Обчисліть: log₂5 + log₂1,6

А	Б	В	Г	Д
3	3,3	0,25	4	log2 6,6

 

2) Обчисліть: log₃18 - log₃2

А	Б	В	Г	Д
9	6	log316	3	2

 

3)

А	Б	В	Г	Д
-1	2	1	5	20

 

 

4) Обчисліть: log₉5∙log₅81

А	Б	В	Г	Д
405	45	1	2	0

 

 

5) Обчисліть: log₃+

А	Б	В	Г	Д
-         1	log3	1	log35	0

 

6) Обчисліть значення виразу:

А	Б	В	Г	Д
0	1	3	2	27

 

Перевірка у парах

1	2	3	4	5	6
А	Д	Б	Г	Д	Д
3	2	2	2	0	27

 

VI. Підбиття підсумків  уроку

-         Роз’яснення незрозумілих питань.

-         Самооцінювання робіт учнями.  

-         Оголошення оцінок за урок.

 

VI. Рефлексія

1. Чи задоволений ти своєю роботою на уроці?

     а) так;     б) частково;
     в) ні;   г) важко відповісти

2. Яким чином ти збираєшся усунути прогалини?
     а) спитати у викладача;      б) спитати у товариша;
     в) впораюсь сам (сама);                         г) не знаю

3. Чи зміг би ти  пояснити  хід  розв‘язку задачі своєму товаришу?
     а) так;     б) частково;

     в) ні;   г) важко відповісти

4. Якій формі роботи на уроці ти надаєш перевагу?
    а) индивідуальній;             б) у парі;                 г) колективній

Твій настрій:

 

                       САМООЦІНКА:                ОЦІНКА ВИКЛАДАЧА:

VIII. Домашнє завдання.

Підручник: Математика: (алгебра і початки аналізу та геометрія, рівень стандарту) для 11 кл.\ О.С. Істер

№ 4.5 (початковий рівень)

№4.21 (середній рівень)

   № 4.38 (достатній рівень)

 № 4.51 (високий рівень)